2021-2022学年北师大版数学九年级上册 第四章 图形的相似 单元检测(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级上册 第四章 图形的相似 单元检测(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览




文档简介
第四章单元检测
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.下列四组线段中,不是成比例线段的是( )
A.0.5,3,2,10 B.3,4,6,2
C.5,6,15,18 D.1.5,4,1.2,5
2.已知=,的值是( )
A. B. C. D.
3.如图,已知直线AB∥CD∥EF,BD=2,DF=4,则的值为( )
A. B. C. D.1
(第3题) (第4题)
4.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,S△ADE ∶S四边形DECB=4 ∶5,则AD ∶DB为( )
A.1 ∶2 B.2 ∶3
C.2 ∶1 D.3 ∶2
5.在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,4),B(-4,0),O(0,0),以原点O为位似中心,把这个三角形放大为原来的2倍,得到△CDO,则点A的对应点C的坐标为( )
A.(-4,8) B.(4,-8)
C.(-4,8)或(4,-8) D.(-1,2)或(1,-2)
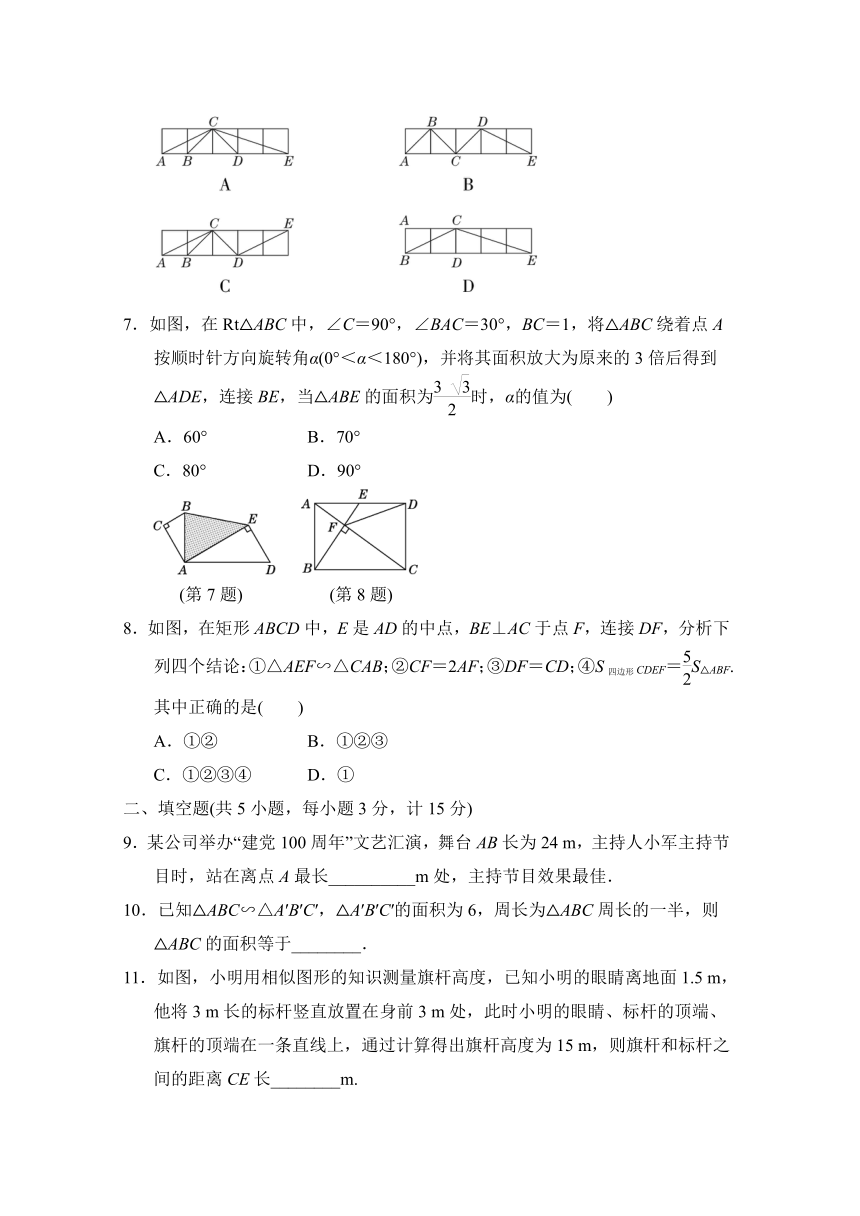
6.下列每个矩形都是由五个同样的小正方形拼合组成的,其中△ABC和△CDE的顶点都在小正方形的顶点上,则△ABC与△CDE一定相似的图形是( )
7.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,将△ABC绕着点A按顺时针方向旋转角α(0°<α<180°),并将其面积放大为原来的3倍后得到△ADE,连接BE,当△ABE的面积为时,α的值为( )
A.60° B.70°
C.80° D.90°
(第7题) (第8题)
8.如图,在矩形ABCD中,E是AD的中点,BE⊥AC于点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=CD;④S四边形CDEF=S△ABF.其中正确的是( )
A.①② B.①②③
C.①②③④ D.①
二、填空题(共5小题,每小题3分,计15分)
9.某公司举办“建党100周年”文艺汇演,舞台AB长为24 m,主持人小军主持节目时,站在离点A最长__________m处,主持节目效果最佳.
10.已知△ABC∽△A′B′C′,△A′B′C′的面积为6,周长为△ABC周长的一半,则△ABC的面积等于________.
11.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5 m,他将3 m长的标杆竖直放置在身前3 m处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算得出旗杆高度为15 m,则旗杆和标杆之间的距离CE长________m.
(第11题) (第12题) (第13题)
12.如图,△OAB与△OCD是以点O为位似中心的位似图形,点B在OD上,AE,CB分别是△OAB,△OCD的中线,则的值为________.
13.如图,点P是矩形ABCD内一点,连接PA,PB,PC,PD,已知AB=3,BC=4,设△PAB,△PBC,△PCD,△PDA的面积分别为S1,S2,S3,S4,给出以下判断:①PA+PB+PC+PD的最小值为10;②若△PAB≌△PCD,则△PAD≌△PBC;③若S1=S2,则S3=S4;④若△PAB∽△PDA,则PA=2.其中正确的是______________(填序号).
三、解答题(共13小题,计81分.解答应写出过程)
14.(本题满分5分)已知==,求的值.
15.(本题满分5分)如图所示,l1∥l2∥l3,且AB=2BC,DF=5 cm,AG=4 cm.求GF,AF,EF的长.
(第15题)
16.(本题满分5分)在如图所示的两个相似的五边形中,试求未知的边x,y,z的长度及角α,β的度数.
(第16题)
17.(本题满分5分)如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,连接BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
(第17题)
18.(本题满分5分)如图,在Rt△ABC中,∠C=90°,AC=4 cm,BC=5 cm,点D在BC上,且CD=3 cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点C运动;点Q以1.25 cm/s的速度沿BC向终点C运动,过点P作PE∥BC交AD于点E,连接EQ,设动点运动时间为t s(t>0).
(1)CP=________,CQ=________.(用含t的代数式表示)
(2)连接PQ,在运动过程中,不论t取何值时,总有线段PQ与线段AB平行,为什么?
(第18题)
19. (本题满分5分)如图,在 ABCD中,DE交BC于点F,交AB的延长线于点E,且∠EDB=∠C.
(第19题)
(1)求证:△ADE∽△DBE;
(2)若DC=7 cm,BE=9 cm,求DE的长.
20.(本题满分5分)如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,BF交AC于点P,且AB=,BC=1.求BP.
(第20题)
21.(本题满分6分)如图①,在等边三角形ABC中,点D是边BC上的动点(不与点B,C重合),点E,F分别在边AB和AC上,且∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)若点D移至BC的中点,如图②,求证:FD平分∠EFC.
(第21题)
22.(本题满分7分)如图是一个小商场的纵截面图(矩形ABCD),AD是商场的顶部,BC是商场的地面,地面由边长为80 cm的正方形瓷砖铺成,从B到C共有25块瓷砖,AB和CD是商场的两面墙壁,MN是顶部正中央的一个长方形的灯饰(AM=DN),小张同学想通过学过的几何知识来测量该商场的高度(AB)和灯饰的长度(MN),于是去商场时带了一面镜子和一根激光笔,他先把激光笔挂在墙壁CD距地面两块砖高度(CG的长)的G处,镜子水平放在地面距离C两块砖的F处,发现激光笔的反射光照到了N处;再把激光笔挂在墙壁AB距地面两块砖高度(LB的长)的L处,镜子水平放在地面距离B三块砖的P处,发现激光笔的反射光恰好又照到了N处,请你帮忙计算AB的高度和MN的长度.
(第22题)
23.(本题满分7分)如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP;
(2)直接回答△ADP与△BCP是不是位似图形;
(3)若AB=8,CD=4,DP=3,求AP的长.
(第23题)
24.(本题满分8分)如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.
(1)请以点O为位似中心,在网格中作出四边形A′B′C′D′,使四边形A′B′C′D′与四边形ABCD位似,且=2;
(2)求线段C′D′的长;
(3)求出△A′D′O的面积.
(第24题)
25.(本题满分8分)如图,在矩形ABCD中,AB=12 cm,BC=6 cm,点E自点A出发,以1 cm/s的速度向点D前进,同时点F从点D以2 cm/s的速度向点C前进,若移动的时间为t s,且0≤t≤6.
(1)当t为多少时,DE=2DF
(2)四边形DEBF的面积是否为定值?若是定值,请求出定值;若不是定值,请说明理由.
(3)以点D,E,F为顶点的三角形能否与△BCD相似?若能,请求出所有可能的t的值;若不能,请说明理由.
(第25题)
26.(本题满分10分)【阅读理解】我们知道,利用相似三角形性质求线段长是常用求线段长的方法之一,如图①,在△ABC中,D为BC上一点,若∠BAD=∠C,可易证△ABD∽△CBA,从而可得AB2=BD·BC,若已知其中两条线段的长即可求出第三条线段的长.
(1)【尝试应用】如图②,在 BCEF中,D为BC上一点,E为AC上一点,∠BAD=∠C,若AB=8,BD=5,求EF的长.
(2)【拓展应用】如图③,在正方形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,∠EDF=45°,EF=8,DE=12,请求出正方形ABCD的边长.
(第26题)
答案
一、1.A 2.C 3.A 4.C 5.C 6.A 7.D 8.C
二、9.(12 -12) 10.24 11.24
12. 13.①②③
三、14. 解:设===k,则a+b=3k,b+c=4k,c+a=5k,解得a=2k,b=k,c=3k,
所以==-1.
15.解:∵l2∥l3,∴=.
而AG=4 cm,AB=2BC,
∴=2.∴GF=2 cm.
∴AF=AG+GF=4+2=6(cm).
∵l1∥l2∥l3,
∴=,即=,
∴EF=cm.
16.解:因为两个五边形相似,所以===,β=58°.
解得x=0.8,y=0.6,z=1,α=540°-100°-170°-58°-72°=140°.
17.解:(1)∵AD平分∠BAC,
∠BAC=60°,∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,
∠DAC=30°,AC=6,∴CD=2 ,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,∴BC=6 ,
∴BD=BC-CD=4 ,
∵DE∥CA,
∴==,∴DE=4;
(2)如图.
(第17题)
∵点M是线段AD的中点,
∴DM=AM,∵DE∥CA,
∴=.∴DF=AG.
∵DE∥CA,∴=,=.
∴=.∵BD=4 , BC=6 , DF=AG,∴=.
18.解:(1)(4-t)cm;(5-1.25 t)cm
(2)由(1)知PC=(4-t)cm,QC=(5-1.25t)cm,
∴==1-,
==1-.
∴=,
∵∠C=90°,∴△ABC∽△PQC,
∴∠PQC=∠B,∴PQ∥AB.
∴不论t取何值时,总有线段PQ与线段AB平行.
19.(1)证明: ABCD中,∠A=∠C,∵∠EDB=∠C,
∴∠A=∠EDB,又∵∠E=∠E,
∴△ADE∽△DBE;
(2)解: ABCD中,
DC=AB,由(1)得△ADE∽△DBE,
∴=,
∵DC=7 cm,BE=9 cm,
∴AB=7 cm,AE=16 cm.
∴DE=12 cm.
20.解:∵△ABC,△DCE,△FEG是三个全等的等腰三角形,
∴FG=AB=,GE=BC=1,
BG=3BC=3,
∴=,==.
∴=.∵∠FGE=∠BGF,
∴△BFG∽△FEG.∴=.
∵FG=FE,∴BF=BG=3.
∵∠ACB=∠G,∴AC∥FG,
∴==,
∴BP=BF=1.
21.证明:(1)∵△ABC是等边三角形,∴∠B=∠C=60°,
∵∠BED+∠B=∠EDF+∠FDC,∠EDF=60°,
∴∠BED=∠CDF,
∴△BDE∽△CFD;
(2)∵△BDE∽△CFD,∴=.
∵BD=CD,∴=.
∵∠EDF=∠C=60°,
∴△DFE∽△CFD.
∴∠EFD=∠CFD.
∴FD平分∠EFC.
22.解:过点N作NT⊥BC于点T,则四边形ABTN,四边形CDNT都是矩形,设AB=NT=CD=x cm.
由题意,得BC=80×25=2 000(cm),CG=CF=LB=2×80=160(cm),BP=3×80=240(cm),∵∠B=∠PTN=90°,∠NPT=∠LPB,
∴△LBP∽△NTP,∴=,
∴=,∴PT=x,
同法可证,△GCF∽△NTF,可得FT=NT=x cm,
∵BP+PT+TF+CF=2 000 cm,
∴240+x+x+160=2 000,
∴x=640,∴DN=CT=800 cm,
AB=CD=640 cm,∴AM=DN=800 cm,∴MN=AD-AM-DN=2 000-1 600=400(cm).
23.(1)证明:∵∠DAP=∠CBP,∠DPA=∠CPB,∴△ADP∽△BCP.
(2)解:△ADP与△BCP不是位似图形.
(3)解:∵△ADP∽△BCP,
∴=,又∵∠APB=∠DPC,
∴△APB∽△DPC,∴=,
即=,解得AP=6.
24.解:(1)如图所示,四边形A′B′C′D′即为所求.
(第24题)
(2)线段C′D′的长为=4 .
(3)△A′D′O的面积为×(4+2)×6-×4×2-×4×2=10.
25.解:(1)由题意,得DE=AD-t=6-t,DF=2t,
∴6-t=2×2t,解得t=,
故当t=时,DE=2DF.
(2)四边形DEBF的面积是定值.
∵矩形ABCD的面积为12×6=72(cm2),S△ABE=×12×t=6t(cm2),S△BCF=×6×(12-2t)=36-6t(cm2),
∴四边形DEBF的面积=矩形的面积-S△ABE-S△BCF=72-6t-36+6t=36(cm2),故四边形DEBF的面积为定值.
(3)设以点D,E,F为顶点的三角形能与△BCD相似,
则=或=,
由ED=(6-t)cm,DF=2t cm,CD=12 cm,BC=6 cm,代入,得=或=,解得t=3或t=,
故当t=3或时,以点D,E,F为顶点的三角形与△BCD相似.
26. 解:(1)∵∠BAD=∠C,∠ABD=∠CBA,∴△ABD∽△CBA,
∴=,即=,
解得BC=.
∵四边形BCEF为平行四边形,
∴EF=BC=.
(2)分别延长EF,DC相交于点G,
∵四边形ABCD是正方形,
∴∠ACD=45°,AC=AD,
∵EF∥AC,∴∠EGD=∠ACD=45°,
∵∠EDF=45°,∴∠EDF=∠EGD,
∵∠E=∠E,∴△EDF∽△EGD,
∴=,即=,
解得EG=18,
∵AC∥EG,AB∥CD,
∴四边形AEGC为平行四边形,
∴AC=EG=18,
∴AD=×18=9 .
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.下列四组线段中,不是成比例线段的是( )
A.0.5,3,2,10 B.3,4,6,2
C.5,6,15,18 D.1.5,4,1.2,5
2.已知=,的值是( )
A. B. C. D.
3.如图,已知直线AB∥CD∥EF,BD=2,DF=4,则的值为( )
A. B. C. D.1
(第3题) (第4题)
4.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,S△ADE ∶S四边形DECB=4 ∶5,则AD ∶DB为( )
A.1 ∶2 B.2 ∶3
C.2 ∶1 D.3 ∶2
5.在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,4),B(-4,0),O(0,0),以原点O为位似中心,把这个三角形放大为原来的2倍,得到△CDO,则点A的对应点C的坐标为( )
A.(-4,8) B.(4,-8)
C.(-4,8)或(4,-8) D.(-1,2)或(1,-2)
6.下列每个矩形都是由五个同样的小正方形拼合组成的,其中△ABC和△CDE的顶点都在小正方形的顶点上,则△ABC与△CDE一定相似的图形是( )
7.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,将△ABC绕着点A按顺时针方向旋转角α(0°<α<180°),并将其面积放大为原来的3倍后得到△ADE,连接BE,当△ABE的面积为时,α的值为( )
A.60° B.70°
C.80° D.90°
(第7题) (第8题)
8.如图,在矩形ABCD中,E是AD的中点,BE⊥AC于点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=CD;④S四边形CDEF=S△ABF.其中正确的是( )
A.①② B.①②③
C.①②③④ D.①
二、填空题(共5小题,每小题3分,计15分)
9.某公司举办“建党100周年”文艺汇演,舞台AB长为24 m,主持人小军主持节目时,站在离点A最长__________m处,主持节目效果最佳.
10.已知△ABC∽△A′B′C′,△A′B′C′的面积为6,周长为△ABC周长的一半,则△ABC的面积等于________.
11.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5 m,他将3 m长的标杆竖直放置在身前3 m处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算得出旗杆高度为15 m,则旗杆和标杆之间的距离CE长________m.
(第11题) (第12题) (第13题)
12.如图,△OAB与△OCD是以点O为位似中心的位似图形,点B在OD上,AE,CB分别是△OAB,△OCD的中线,则的值为________.
13.如图,点P是矩形ABCD内一点,连接PA,PB,PC,PD,已知AB=3,BC=4,设△PAB,△PBC,△PCD,△PDA的面积分别为S1,S2,S3,S4,给出以下判断:①PA+PB+PC+PD的最小值为10;②若△PAB≌△PCD,则△PAD≌△PBC;③若S1=S2,则S3=S4;④若△PAB∽△PDA,则PA=2.其中正确的是______________(填序号).
三、解答题(共13小题,计81分.解答应写出过程)
14.(本题满分5分)已知==,求的值.
15.(本题满分5分)如图所示,l1∥l2∥l3,且AB=2BC,DF=5 cm,AG=4 cm.求GF,AF,EF的长.
(第15题)
16.(本题满分5分)在如图所示的两个相似的五边形中,试求未知的边x,y,z的长度及角α,β的度数.
(第16题)
17.(本题满分5分)如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,连接BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
(第17题)
18.(本题满分5分)如图,在Rt△ABC中,∠C=90°,AC=4 cm,BC=5 cm,点D在BC上,且CD=3 cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点C运动;点Q以1.25 cm/s的速度沿BC向终点C运动,过点P作PE∥BC交AD于点E,连接EQ,设动点运动时间为t s(t>0).
(1)CP=________,CQ=________.(用含t的代数式表示)
(2)连接PQ,在运动过程中,不论t取何值时,总有线段PQ与线段AB平行,为什么?
(第18题)
19. (本题满分5分)如图,在 ABCD中,DE交BC于点F,交AB的延长线于点E,且∠EDB=∠C.
(第19题)
(1)求证:△ADE∽△DBE;
(2)若DC=7 cm,BE=9 cm,求DE的长.
20.(本题满分5分)如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,BF交AC于点P,且AB=,BC=1.求BP.
(第20题)
21.(本题满分6分)如图①,在等边三角形ABC中,点D是边BC上的动点(不与点B,C重合),点E,F分别在边AB和AC上,且∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)若点D移至BC的中点,如图②,求证:FD平分∠EFC.
(第21题)
22.(本题满分7分)如图是一个小商场的纵截面图(矩形ABCD),AD是商场的顶部,BC是商场的地面,地面由边长为80 cm的正方形瓷砖铺成,从B到C共有25块瓷砖,AB和CD是商场的两面墙壁,MN是顶部正中央的一个长方形的灯饰(AM=DN),小张同学想通过学过的几何知识来测量该商场的高度(AB)和灯饰的长度(MN),于是去商场时带了一面镜子和一根激光笔,他先把激光笔挂在墙壁CD距地面两块砖高度(CG的长)的G处,镜子水平放在地面距离C两块砖的F处,发现激光笔的反射光照到了N处;再把激光笔挂在墙壁AB距地面两块砖高度(LB的长)的L处,镜子水平放在地面距离B三块砖的P处,发现激光笔的反射光恰好又照到了N处,请你帮忙计算AB的高度和MN的长度.
(第22题)
23.(本题满分7分)如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP;
(2)直接回答△ADP与△BCP是不是位似图形;
(3)若AB=8,CD=4,DP=3,求AP的长.
(第23题)
24.(本题满分8分)如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.
(1)请以点O为位似中心,在网格中作出四边形A′B′C′D′,使四边形A′B′C′D′与四边形ABCD位似,且=2;
(2)求线段C′D′的长;
(3)求出△A′D′O的面积.
(第24题)
25.(本题满分8分)如图,在矩形ABCD中,AB=12 cm,BC=6 cm,点E自点A出发,以1 cm/s的速度向点D前进,同时点F从点D以2 cm/s的速度向点C前进,若移动的时间为t s,且0≤t≤6.
(1)当t为多少时,DE=2DF
(2)四边形DEBF的面积是否为定值?若是定值,请求出定值;若不是定值,请说明理由.
(3)以点D,E,F为顶点的三角形能否与△BCD相似?若能,请求出所有可能的t的值;若不能,请说明理由.
(第25题)
26.(本题满分10分)【阅读理解】我们知道,利用相似三角形性质求线段长是常用求线段长的方法之一,如图①,在△ABC中,D为BC上一点,若∠BAD=∠C,可易证△ABD∽△CBA,从而可得AB2=BD·BC,若已知其中两条线段的长即可求出第三条线段的长.
(1)【尝试应用】如图②,在 BCEF中,D为BC上一点,E为AC上一点,∠BAD=∠C,若AB=8,BD=5,求EF的长.
(2)【拓展应用】如图③,在正方形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,∠EDF=45°,EF=8,DE=12,请求出正方形ABCD的边长.
(第26题)
答案
一、1.A 2.C 3.A 4.C 5.C 6.A 7.D 8.C
二、9.(12 -12) 10.24 11.24
12. 13.①②③
三、14. 解:设===k,则a+b=3k,b+c=4k,c+a=5k,解得a=2k,b=k,c=3k,
所以==-1.
15.解:∵l2∥l3,∴=.
而AG=4 cm,AB=2BC,
∴=2.∴GF=2 cm.
∴AF=AG+GF=4+2=6(cm).
∵l1∥l2∥l3,
∴=,即=,
∴EF=cm.
16.解:因为两个五边形相似,所以===,β=58°.
解得x=0.8,y=0.6,z=1,α=540°-100°-170°-58°-72°=140°.
17.解:(1)∵AD平分∠BAC,
∠BAC=60°,∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,
∠DAC=30°,AC=6,∴CD=2 ,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,∴BC=6 ,
∴BD=BC-CD=4 ,
∵DE∥CA,
∴==,∴DE=4;
(2)如图.
(第17题)
∵点M是线段AD的中点,
∴DM=AM,∵DE∥CA,
∴=.∴DF=AG.
∵DE∥CA,∴=,=.
∴=.∵BD=4 , BC=6 , DF=AG,∴=.
18.解:(1)(4-t)cm;(5-1.25 t)cm
(2)由(1)知PC=(4-t)cm,QC=(5-1.25t)cm,
∴==1-,
==1-.
∴=,
∵∠C=90°,∴△ABC∽△PQC,
∴∠PQC=∠B,∴PQ∥AB.
∴不论t取何值时,总有线段PQ与线段AB平行.
19.(1)证明: ABCD中,∠A=∠C,∵∠EDB=∠C,
∴∠A=∠EDB,又∵∠E=∠E,
∴△ADE∽△DBE;
(2)解: ABCD中,
DC=AB,由(1)得△ADE∽△DBE,
∴=,
∵DC=7 cm,BE=9 cm,
∴AB=7 cm,AE=16 cm.
∴DE=12 cm.
20.解:∵△ABC,△DCE,△FEG是三个全等的等腰三角形,
∴FG=AB=,GE=BC=1,
BG=3BC=3,
∴=,==.
∴=.∵∠FGE=∠BGF,
∴△BFG∽△FEG.∴=.
∵FG=FE,∴BF=BG=3.
∵∠ACB=∠G,∴AC∥FG,
∴==,
∴BP=BF=1.
21.证明:(1)∵△ABC是等边三角形,∴∠B=∠C=60°,
∵∠BED+∠B=∠EDF+∠FDC,∠EDF=60°,
∴∠BED=∠CDF,
∴△BDE∽△CFD;
(2)∵△BDE∽△CFD,∴=.
∵BD=CD,∴=.
∵∠EDF=∠C=60°,
∴△DFE∽△CFD.
∴∠EFD=∠CFD.
∴FD平分∠EFC.
22.解:过点N作NT⊥BC于点T,则四边形ABTN,四边形CDNT都是矩形,设AB=NT=CD=x cm.
由题意,得BC=80×25=2 000(cm),CG=CF=LB=2×80=160(cm),BP=3×80=240(cm),∵∠B=∠PTN=90°,∠NPT=∠LPB,
∴△LBP∽△NTP,∴=,
∴=,∴PT=x,
同法可证,△GCF∽△NTF,可得FT=NT=x cm,
∵BP+PT+TF+CF=2 000 cm,
∴240+x+x+160=2 000,
∴x=640,∴DN=CT=800 cm,
AB=CD=640 cm,∴AM=DN=800 cm,∴MN=AD-AM-DN=2 000-1 600=400(cm).
23.(1)证明:∵∠DAP=∠CBP,∠DPA=∠CPB,∴△ADP∽△BCP.
(2)解:△ADP与△BCP不是位似图形.
(3)解:∵△ADP∽△BCP,
∴=,又∵∠APB=∠DPC,
∴△APB∽△DPC,∴=,
即=,解得AP=6.
24.解:(1)如图所示,四边形A′B′C′D′即为所求.
(第24题)
(2)线段C′D′的长为=4 .
(3)△A′D′O的面积为×(4+2)×6-×4×2-×4×2=10.
25.解:(1)由题意,得DE=AD-t=6-t,DF=2t,
∴6-t=2×2t,解得t=,
故当t=时,DE=2DF.
(2)四边形DEBF的面积是定值.
∵矩形ABCD的面积为12×6=72(cm2),S△ABE=×12×t=6t(cm2),S△BCF=×6×(12-2t)=36-6t(cm2),
∴四边形DEBF的面积=矩形的面积-S△ABE-S△BCF=72-6t-36+6t=36(cm2),故四边形DEBF的面积为定值.
(3)设以点D,E,F为顶点的三角形能与△BCD相似,
则=或=,
由ED=(6-t)cm,DF=2t cm,CD=12 cm,BC=6 cm,代入,得=或=,解得t=3或t=,
故当t=3或时,以点D,E,F为顶点的三角形与△BCD相似.
26. 解:(1)∵∠BAD=∠C,∠ABD=∠CBA,∴△ABD∽△CBA,
∴=,即=,
解得BC=.
∵四边形BCEF为平行四边形,
∴EF=BC=.
(2)分别延长EF,DC相交于点G,
∵四边形ABCD是正方形,
∴∠ACD=45°,AC=AD,
∵EF∥AC,∴∠EGD=∠ACD=45°,
∵∠EDF=45°,∴∠EDF=∠EGD,
∵∠E=∠E,∴△EDF∽△EGD,
∴=,即=,
解得EG=18,
∵AC∥EG,AB∥CD,
∴四边形AEGC为平行四边形,
∴AC=EG=18,
∴AD=×18=9 .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
