2021--2022学年北师大版九年级数学下册1.6利用三角函数测高同步测试(word版 含答案)
文档属性
| 名称 | 2021--2022学年北师大版九年级数学下册1.6利用三角函数测高同步测试(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 233.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 09:47:16 | ||
图片预览




文档简介
北师大版九年级数学下册第一章1.6利用三角函数测高
一.选择题
1.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
A.2海里 B.2sin55°海里 C.2cos55°海里 D.2tan55°海里
2. 如图,小颖家(图中点处)门前有一条东西走向的公路,经测得有一水塔(图中点处)在距她家北偏东方向的米处,那么水塔所在的位置到公路的距离是( )
A.米 B.米
C.米 D.米
3. 如图,港口在观测站的正东方向,,某船从港口出发,沿北偏东方向航行一段距离后到达处,此时从观测站处测得该船位于北偏东的方向,则该船航行的距离(即的长)为( )
A. B.
C. D.
4. 一艘观光游船从港口以北偏东的方向出港观光,航行海里至处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东方向,马上以每小时海里的速度前往救援,则海警船到达事故船处所需的时间大约为(单位:小时)( )
A. B. C. D.
5.如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
A.12.1m B.13.3m C.16.9m D.18.1m
6.如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
A.100 B.200 C.100 D.200
7.如图,为测量一根与地面垂直的旗杆AH的高度,在距离旗杆底端H10米的B处测得旗杆顶端A的仰角∠ABH=α,则旗杆AH的高度为( )
A.10sinα米 B.10cosα米 C.米 D.10tanα米
8. 如图,飞机在目标的正上方,在地面处测得飞机的仰角为,在飞机上测得地面处的俯角为,飞行高度为,间距离为,从这个已知量中任取个为一组,共有组,那么可以求出间距离的有( )
A.组 B.组 C.组 D.组
9. 如图,小丽用一个两锐角分别为和的三角尺测量一棵树的高度,已知她与树之间的距离为,眼睛与地面的距离为,那么这棵树的高度大约是( )
A. B. C. D.
10. 如图,为了测得电视塔的高度,在处用高为米的测角仪,测得电视塔顶端的仰角为,再向电视塔方向前进米达到处,又测得电视塔顶端的仰角为,则这个电视塔的高度(单位:米)为( )
A. B. C. D.
二.填空题
11.如图,海中有一小岛A,它周围10.5海里内有暗礁,渔船跟踪鱼群由西向东航行.在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,那么渔船还需航行 海里就开始有触礁的危险.
12.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3 m,cos∠BAC=,
则墙高BC=________.
13.如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为 米.
14.从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是 .
15. 如图,一艘海轮位于灯塔的北偏东方向,距离灯塔为海里的点处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离为________海里.
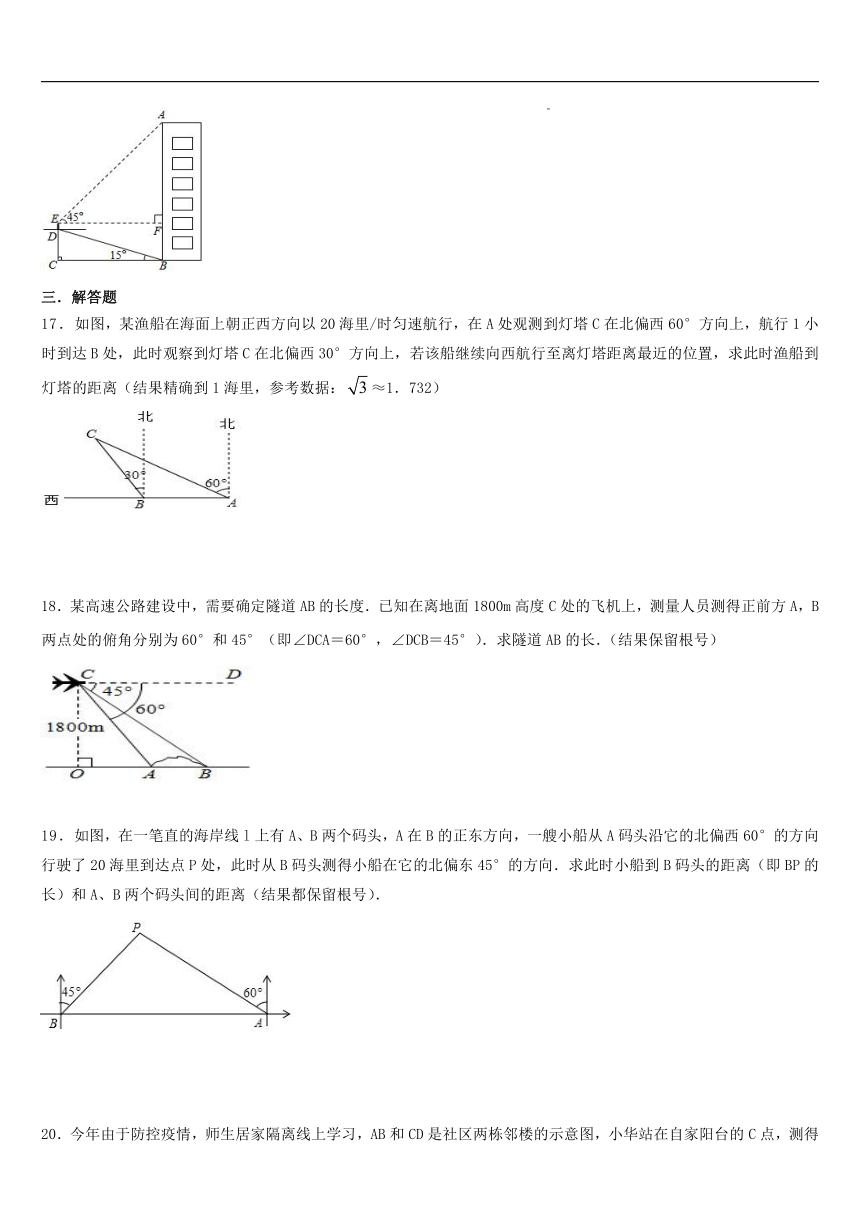
16.小致为了测量楼房AB的高度,他从楼底的B处沿着斜坡行走20m,达到坡顶D处.已知斜坡的坡角为15°,小致的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,则楼房AB的高度为 m.(计算结果精确到1m,参考数据:sin15°=,cos15°=,tan15°=.)
三.解答题
17.如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:≈1.732)
18.某高速公路建设中,需要确定隧道AB的长度.已知在离地面1800m高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°(即∠DCA=60°,∠DCB=45°).求隧道AB的长.(结果保留根号)
19.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
20.今年由于防控疫情,师生居家隔离线上学习,AB和CD是社区两栋邻楼的示意图,小华站在自家阳台的C点,测得对面楼顶点A的仰角为30°,地面点E的俯角为45°.点E在线段BD上,测得B,E间距离为8.7米,楼AB高12米.求小华家阳台距地面高度CD的长.(结果精确到1米,≈1.41,≈1.73)
21.如图,某公路局施工队要修建一条东西方向的公路MN,已知C点周围100米范围内为古建筑保护群,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走400米到达B处,测得C在点B的北偏西60°方向上.(参考数据:≈1.414,≈1.732)
(1)MN是否穿过古建筑保护群?为什么?
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高20%,则原计划完成这项工程需要多少天?
22.如图,在某次军事演习时,中国空警机A在北偏东22°方向上发现有不明敌机在钓鱼岛P附近徘徊,并快速报告给东海司令部.此时正在空警机A的正西方向200km处巡逻的中国歼击机B接到任务,迅速赶往北偏东60°方向上的钓鱼岛P处,已知歼击机B的速度是2.2马赫(1马赫大约等于1200km/h).请根据以上信息,求出歼击机B到达钓鱼岛P所需的时间.(结果精确到1s.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.73)
23.某公园中有条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨利用它们测量小河的宽度,于是,他去了河边,如图.他从河的南岸石墩A处测得大树P在其北偏东30°方向,然后他沿正东方向步行80米到达点B处,此时测得大树P在其北偏西60°方向.请根据以上所测得的数据,计算小河的宽度.(结果保留根号)
答案提示
1.C.
2. A
3. A
4. B
5.C
6.B
7.D
8.C
9.B
10.C
11.4.5.
12.答案为: m.
13.答案为:50.
14.答案为:(6+6)米.
15.
16.26.
17.解:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),
∵∠CAF=60°,∠CBE=30°,
∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°-∠CAF=30°,
∴∠C=180°-∠CBA-∠CAB=30°,
∴∠C=∠CAB,
∴BC=BA=20(海里),
∠CBD=90°-∠CBE=60°,
∴CD=BC sin∠CBD=20×≈17(海里).
18.解:由题意得∠CAO=60°,∠CBO=45°,
∵OA=1800×tan30°=1800×=600,OB=OC=1800,
∴AB=(1800﹣600)(m).
答:隧道AB的长为(1800﹣600)m.
19.解:如图:
过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°-45°=45°,∠PAM=90°-60°=30°,AP=20海里,
∴PM= AP=10海里,AM=cos30°AP=10海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10)海里,
∴BP=PM =10海里,
即小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里.
20.解:作CH⊥AB于H,如图所示:
则四边形HBDC为矩形,
∴BD=CH,BH=CD,
由题意得,∠ACH=30°,∠DCE=45°,
设BH=CD=x米,则AH=(12﹣x)米,
在Rt△AHC中,∵tan∠ACH==,
∴HC=AH=(36﹣x)米,
∵∠CDE=90°,
∴∠CED=90°﹣45°=45°=∠DCE,
∴ED=CD=x米,
∵CH=BD=BE+ED
∴8.7+x=36﹣x.
∵≈1.73,
解得x≈10.
答:小华家阳台距地面高度CD的长约为10米.
21.解:(1)不穿过.理由:
过点C作CH⊥AB于H,
设CH=x,由已知∠EAC=45°,∠FBC=60°,
则∠CAH=45°,∠CBH=30°,
在Rt△ACH中,AH=CH=x,
在Rt△BCH中,,
∴,
∴整理化简得,
解得米>100米,
∴MN不会穿过古建筑保护群;
(2)设原计划完成这项工程需要y天,则实际完成工程需要(y﹣5)天.
根据题意得:,
解得:y=30,
经检验:y=30是原方程的根,
答:原计划完成这项工作需要30天.
22.解:过点P作PC⊥BA交BA的延长线于C,
设AC=xkm,则BC=(200+x)km,
在Rt△PAC中,tan∠APC=,
∴PC=≈=2.5x,
在Rt△BCP中,tan∠PBC=,
∴≈,
解得,x≈60,则PC=2.5x=150,
在Rt△PBC中,∠PBC=30°,
∴BP=2PC=300,
∴歼击机B到达钓鱼岛P所需的时间为:×3600≈410(s),
答:歼击机B到达钓鱼岛P所需的时间约为410s.
23.解:如图,作PD⊥AB交CA于点D,
∵∠APD=30°,
∴AD=PD×tan30°=PD,
∵∠BPD=60°,
∴BD=PD×tan60°=PD,
∵AD+BD=80,
∴PD+PD=80,
解得PD=20.
答:这段河的宽为20米.
一.选择题
1.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
A.2海里 B.2sin55°海里 C.2cos55°海里 D.2tan55°海里
2. 如图,小颖家(图中点处)门前有一条东西走向的公路,经测得有一水塔(图中点处)在距她家北偏东方向的米处,那么水塔所在的位置到公路的距离是( )
A.米 B.米
C.米 D.米
3. 如图,港口在观测站的正东方向,,某船从港口出发,沿北偏东方向航行一段距离后到达处,此时从观测站处测得该船位于北偏东的方向,则该船航行的距离(即的长)为( )
A. B.
C. D.
4. 一艘观光游船从港口以北偏东的方向出港观光,航行海里至处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东方向,马上以每小时海里的速度前往救援,则海警船到达事故船处所需的时间大约为(单位:小时)( )
A. B. C. D.
5.如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
A.12.1m B.13.3m C.16.9m D.18.1m
6.如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
A.100 B.200 C.100 D.200
7.如图,为测量一根与地面垂直的旗杆AH的高度,在距离旗杆底端H10米的B处测得旗杆顶端A的仰角∠ABH=α,则旗杆AH的高度为( )
A.10sinα米 B.10cosα米 C.米 D.10tanα米
8. 如图,飞机在目标的正上方,在地面处测得飞机的仰角为,在飞机上测得地面处的俯角为,飞行高度为,间距离为,从这个已知量中任取个为一组,共有组,那么可以求出间距离的有( )
A.组 B.组 C.组 D.组
9. 如图,小丽用一个两锐角分别为和的三角尺测量一棵树的高度,已知她与树之间的距离为,眼睛与地面的距离为,那么这棵树的高度大约是( )
A. B. C. D.
10. 如图,为了测得电视塔的高度,在处用高为米的测角仪,测得电视塔顶端的仰角为,再向电视塔方向前进米达到处,又测得电视塔顶端的仰角为,则这个电视塔的高度(单位:米)为( )
A. B. C. D.
二.填空题
11.如图,海中有一小岛A,它周围10.5海里内有暗礁,渔船跟踪鱼群由西向东航行.在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,那么渔船还需航行 海里就开始有触礁的危险.
12.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3 m,cos∠BAC=,
则墙高BC=________.
13.如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为 米.
14.从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是 .
15. 如图,一艘海轮位于灯塔的北偏东方向,距离灯塔为海里的点处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离为________海里.
16.小致为了测量楼房AB的高度,他从楼底的B处沿着斜坡行走20m,达到坡顶D处.已知斜坡的坡角为15°,小致的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,则楼房AB的高度为 m.(计算结果精确到1m,参考数据:sin15°=,cos15°=,tan15°=.)
三.解答题
17.如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:≈1.732)
18.某高速公路建设中,需要确定隧道AB的长度.已知在离地面1800m高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°(即∠DCA=60°,∠DCB=45°).求隧道AB的长.(结果保留根号)
19.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
20.今年由于防控疫情,师生居家隔离线上学习,AB和CD是社区两栋邻楼的示意图,小华站在自家阳台的C点,测得对面楼顶点A的仰角为30°,地面点E的俯角为45°.点E在线段BD上,测得B,E间距离为8.7米,楼AB高12米.求小华家阳台距地面高度CD的长.(结果精确到1米,≈1.41,≈1.73)
21.如图,某公路局施工队要修建一条东西方向的公路MN,已知C点周围100米范围内为古建筑保护群,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走400米到达B处,测得C在点B的北偏西60°方向上.(参考数据:≈1.414,≈1.732)
(1)MN是否穿过古建筑保护群?为什么?
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高20%,则原计划完成这项工程需要多少天?
22.如图,在某次军事演习时,中国空警机A在北偏东22°方向上发现有不明敌机在钓鱼岛P附近徘徊,并快速报告给东海司令部.此时正在空警机A的正西方向200km处巡逻的中国歼击机B接到任务,迅速赶往北偏东60°方向上的钓鱼岛P处,已知歼击机B的速度是2.2马赫(1马赫大约等于1200km/h).请根据以上信息,求出歼击机B到达钓鱼岛P所需的时间.(结果精确到1s.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.73)
23.某公园中有条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨利用它们测量小河的宽度,于是,他去了河边,如图.他从河的南岸石墩A处测得大树P在其北偏东30°方向,然后他沿正东方向步行80米到达点B处,此时测得大树P在其北偏西60°方向.请根据以上所测得的数据,计算小河的宽度.(结果保留根号)
答案提示
1.C.
2. A
3. A
4. B
5.C
6.B
7.D
8.C
9.B
10.C
11.4.5.
12.答案为: m.
13.答案为:50.
14.答案为:(6+6)米.
15.
16.26.
17.解:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),
∵∠CAF=60°,∠CBE=30°,
∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°-∠CAF=30°,
∴∠C=180°-∠CBA-∠CAB=30°,
∴∠C=∠CAB,
∴BC=BA=20(海里),
∠CBD=90°-∠CBE=60°,
∴CD=BC sin∠CBD=20×≈17(海里).
18.解:由题意得∠CAO=60°,∠CBO=45°,
∵OA=1800×tan30°=1800×=600,OB=OC=1800,
∴AB=(1800﹣600)(m).
答:隧道AB的长为(1800﹣600)m.
19.解:如图:
过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°-45°=45°,∠PAM=90°-60°=30°,AP=20海里,
∴PM= AP=10海里,AM=cos30°AP=10海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10)海里,
∴BP=PM =10海里,
即小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里.
20.解:作CH⊥AB于H,如图所示:
则四边形HBDC为矩形,
∴BD=CH,BH=CD,
由题意得,∠ACH=30°,∠DCE=45°,
设BH=CD=x米,则AH=(12﹣x)米,
在Rt△AHC中,∵tan∠ACH==,
∴HC=AH=(36﹣x)米,
∵∠CDE=90°,
∴∠CED=90°﹣45°=45°=∠DCE,
∴ED=CD=x米,
∵CH=BD=BE+ED
∴8.7+x=36﹣x.
∵≈1.73,
解得x≈10.
答:小华家阳台距地面高度CD的长约为10米.
21.解:(1)不穿过.理由:
过点C作CH⊥AB于H,
设CH=x,由已知∠EAC=45°,∠FBC=60°,
则∠CAH=45°,∠CBH=30°,
在Rt△ACH中,AH=CH=x,
在Rt△BCH中,,
∴,
∴整理化简得,
解得米>100米,
∴MN不会穿过古建筑保护群;
(2)设原计划完成这项工程需要y天,则实际完成工程需要(y﹣5)天.
根据题意得:,
解得:y=30,
经检验:y=30是原方程的根,
答:原计划完成这项工作需要30天.
22.解:过点P作PC⊥BA交BA的延长线于C,
设AC=xkm,则BC=(200+x)km,
在Rt△PAC中,tan∠APC=,
∴PC=≈=2.5x,
在Rt△BCP中,tan∠PBC=,
∴≈,
解得,x≈60,则PC=2.5x=150,
在Rt△PBC中,∠PBC=30°,
∴BP=2PC=300,
∴歼击机B到达钓鱼岛P所需的时间为:×3600≈410(s),
答:歼击机B到达钓鱼岛P所需的时间约为410s.
23.解:如图,作PD⊥AB交CA于点D,
∵∠APD=30°,
∴AD=PD×tan30°=PD,
∵∠BPD=60°,
∴BD=PD×tan60°=PD,
∵AD+BD=80,
∴PD+PD=80,
解得PD=20.
答:这段河的宽为20米.
