苏科版九年级数学下册 7.2《正弦余弦》教案及课堂检测
文档属性
| 名称 | 苏科版九年级数学下册 7.2《正弦余弦》教案及课堂检测 |

|
|
| 格式 | docx | ||
| 文件大小 | 236.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 17:39:15 | ||
图片预览

文档简介
7.2 正弦与余弦
一、教学目标:
1.理解并掌握正弦、余弦的定义
2.能够运用sinA,cosA表示直角三角形中两边的比
3.通过合作交流,能够根据直角三角形中边角关系进行简单的计算
4.体会数形结合思想在实际问题的运用。
二、学情分析
正弦和余弦是研究直角三角形中边角之间的关系,在解决问题时有着广泛的运用,本节课学生在学习正切的基础上运用类比思想学习,是锐角三角函数意义的完善,深化和延伸,是进一步感受数形结合思想,体会数形结合的方法。
三、重点难点
重点:理解并运用正弦、余弦表示直角三角形中两边的比。
难点:裂解正弦、余弦的概念,用函数观点理解正弦、余弦。
教学活动
【导入】复习回顾
1、在Rt△ABC 中,∠C=90°
tanA= tanB=
2、在Rt△ABC 中,∠C=90°,现把这个三角形的三边都扩大3倍,则∠A的正切值 ( )
A、扩大3倍 B、缩小3倍
C、不变 D、无法确定
3、已知a=tan50,b=tan350,c=tan150, 则a、b、c的大小关系是
【活动】自学书P100,回答下列问题
1、小明沿着该坡道行走了26m,那么他的位置沿垂直方向上升多少 行走了a m呢 你是怎么求出来的
2、小明在水平方向又分别前进了多远
3、如果直角三角形的一个锐角的大小确定,那么这个锐角的对边与斜边的比值、邻边与斜边的比值是否也确定。你是如何得知的
4、锐角的正弦、余弦的概念是什么
5、什么是∠A的三角函数
【讲授】针对问题讲解
在△ABC中, ∠C=90°.
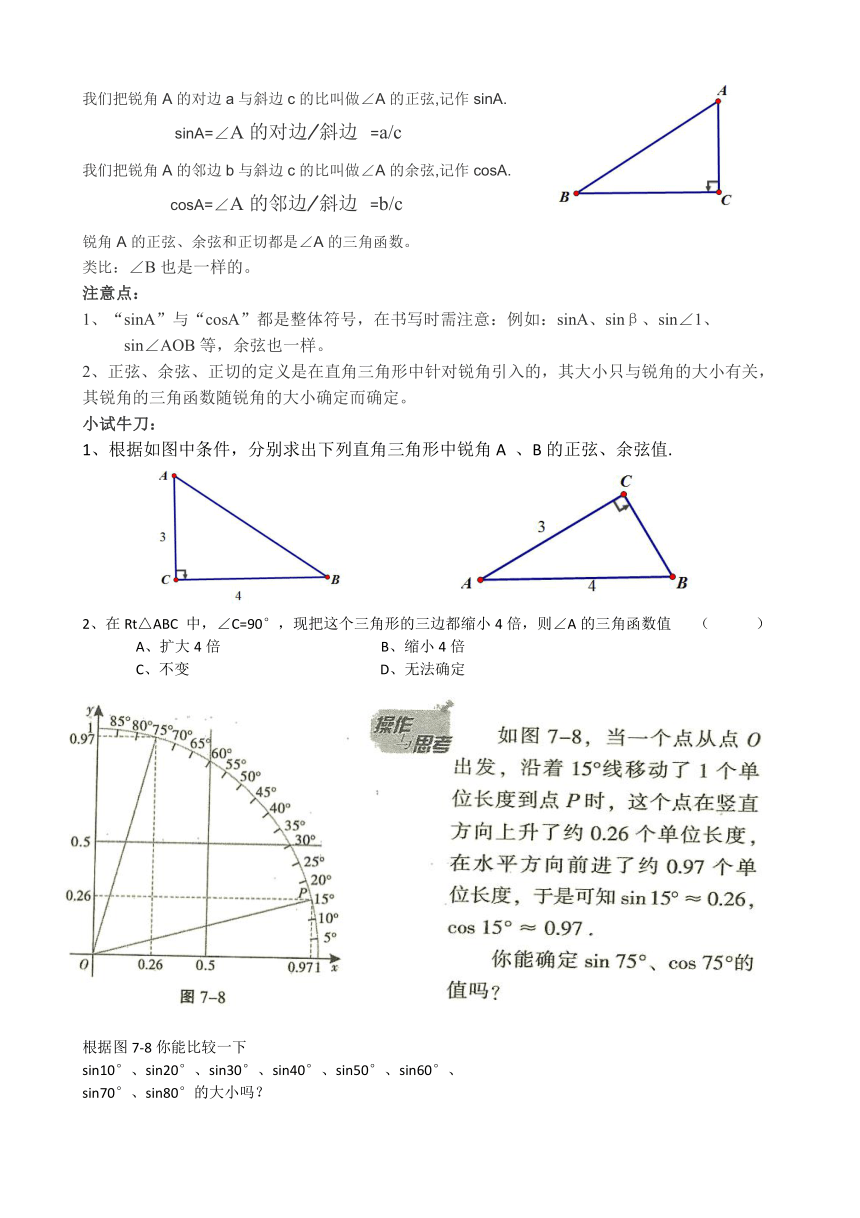
我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
sinA=∠A的对边/斜边 =a/c
我们把锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
cosA=∠A的邻边/斜边 =b/c
锐角A的正弦、余弦和正切都是∠A的三角函数。
类比:∠B也是一样的。
注意点:
“sinA”与“cosA”都是整体符号,在书写时需注意:例如:sinA、sinβ、sin∠1、
sin∠AOB等,余弦也一样。
2、正弦、余弦、正切的定义是在直角三角形中针对锐角引入的,其大小只与锐角的大小有关,其锐角的三角函数随锐角的大小确定而确定。
小试牛刀:
1、根据如图中条件,分别求出下列直角三角形中锐角A 、B的正弦、余弦值.
2、在Rt△ABC 中,∠C=90°,现把这个三角形的三边都缩小4倍,则∠A的三角函数值 ( )
A、扩大4倍 B、缩小4倍
C、不变 D、无法确定
根据图7-8你能比较一下
sin10°、sin20°、sin30°、sin40°、sin50°、sin60°、
sin70°、sin80°的大小吗?
同样:cos10°——cos80°呢?
借助计算器 ,求值(精确到0.01):
结论:当锐角α越来越大时,它的正弦值 ; 余弦值 。
现学现用:
1、已知a=sin32°,b=sin41°,c=sin29°, 则a、b、c的大小是 。
2、已知a=cos32°,b=cos41°,c=cos29°,则a、b、c的大小是 。
例题解析
例1、在Rt△ABC中,∠ACB=90°,若cosA=
求sinA、tanB的值
变式:1、在Rt△ABC中,∠ACB=90°,若sinA=
求tanA、cosA的值
变式:2、在Rt△ABC中,∠ACB=90°,若tanB=
求sinA、cosA的值
例2: 已知:如图,在Rt△ABC中 ∠ACB=90°,CD⊥AB,垂足为D,AC=12,,BC=5,求∠BCD的三角函数值。
(
A
)变式:如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且,AB=4,则AD= .
(
α
) (
D
)
(
E
)
(
C
) (
B
)
拓展延伸
1、如图,△ABC 的三个顶点分别在正方形网格的格点上,则cosA=_______
2、如图,等腰△ABC的周长为16,一边长是 6,则底角的正弦值= 。
课堂检测
班级 姓名
1.在△ABC中, ∠C=90°,AB=2,AC=1,则sinB=_____.
2.在Rt△ABC中, ∠C=90°.AB=3AC.则sinA=______,cosA=_____。
3、已知a=cos35° ,b=cos54°,c=cos42°,则a、b、c的大小关系是 。
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AC=
BC=2,则sin∠ACD= 。
5、在正方形网格中,△ABC的位置如图所示,则cosB= 。
思考题:
如图,正方形ABCD中,E是BC边上一点,以E为圆心、EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,求sin∠EAB的值。
一、教学目标:
1.理解并掌握正弦、余弦的定义
2.能够运用sinA,cosA表示直角三角形中两边的比
3.通过合作交流,能够根据直角三角形中边角关系进行简单的计算
4.体会数形结合思想在实际问题的运用。
二、学情分析
正弦和余弦是研究直角三角形中边角之间的关系,在解决问题时有着广泛的运用,本节课学生在学习正切的基础上运用类比思想学习,是锐角三角函数意义的完善,深化和延伸,是进一步感受数形结合思想,体会数形结合的方法。
三、重点难点
重点:理解并运用正弦、余弦表示直角三角形中两边的比。
难点:裂解正弦、余弦的概念,用函数观点理解正弦、余弦。
教学活动
【导入】复习回顾
1、在Rt△ABC 中,∠C=90°
tanA= tanB=
2、在Rt△ABC 中,∠C=90°,现把这个三角形的三边都扩大3倍,则∠A的正切值 ( )
A、扩大3倍 B、缩小3倍
C、不变 D、无法确定
3、已知a=tan50,b=tan350,c=tan150, 则a、b、c的大小关系是
【活动】自学书P100,回答下列问题
1、小明沿着该坡道行走了26m,那么他的位置沿垂直方向上升多少 行走了a m呢 你是怎么求出来的
2、小明在水平方向又分别前进了多远
3、如果直角三角形的一个锐角的大小确定,那么这个锐角的对边与斜边的比值、邻边与斜边的比值是否也确定。你是如何得知的
4、锐角的正弦、余弦的概念是什么
5、什么是∠A的三角函数
【讲授】针对问题讲解
在△ABC中, ∠C=90°.
我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
sinA=∠A的对边/斜边 =a/c
我们把锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
cosA=∠A的邻边/斜边 =b/c
锐角A的正弦、余弦和正切都是∠A的三角函数。
类比:∠B也是一样的。
注意点:
“sinA”与“cosA”都是整体符号,在书写时需注意:例如:sinA、sinβ、sin∠1、
sin∠AOB等,余弦也一样。
2、正弦、余弦、正切的定义是在直角三角形中针对锐角引入的,其大小只与锐角的大小有关,其锐角的三角函数随锐角的大小确定而确定。
小试牛刀:
1、根据如图中条件,分别求出下列直角三角形中锐角A 、B的正弦、余弦值.
2、在Rt△ABC 中,∠C=90°,现把这个三角形的三边都缩小4倍,则∠A的三角函数值 ( )
A、扩大4倍 B、缩小4倍
C、不变 D、无法确定
根据图7-8你能比较一下
sin10°、sin20°、sin30°、sin40°、sin50°、sin60°、
sin70°、sin80°的大小吗?
同样:cos10°——cos80°呢?
借助计算器 ,求值(精确到0.01):
结论:当锐角α越来越大时,它的正弦值 ; 余弦值 。
现学现用:
1、已知a=sin32°,b=sin41°,c=sin29°, 则a、b、c的大小是 。
2、已知a=cos32°,b=cos41°,c=cos29°,则a、b、c的大小是 。
例题解析
例1、在Rt△ABC中,∠ACB=90°,若cosA=
求sinA、tanB的值
变式:1、在Rt△ABC中,∠ACB=90°,若sinA=
求tanA、cosA的值
变式:2、在Rt△ABC中,∠ACB=90°,若tanB=
求sinA、cosA的值
例2: 已知:如图,在Rt△ABC中 ∠ACB=90°,CD⊥AB,垂足为D,AC=12,,BC=5,求∠BCD的三角函数值。
(
A
)变式:如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且,AB=4,则AD= .
(
α
) (
D
)
(
E
)
(
C
) (
B
)
拓展延伸
1、如图,△ABC 的三个顶点分别在正方形网格的格点上,则cosA=_______
2、如图,等腰△ABC的周长为16,一边长是 6,则底角的正弦值= 。
课堂检测
班级 姓名
1.在△ABC中, ∠C=90°,AB=2,AC=1,则sinB=_____.
2.在Rt△ABC中, ∠C=90°.AB=3AC.则sinA=______,cosA=_____。
3、已知a=cos35° ,b=cos54°,c=cos42°,则a、b、c的大小关系是 。
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AC=
BC=2,则sin∠ACD= 。
5、在正方形网格中,△ABC的位置如图所示,则cosB= 。
思考题:
如图,正方形ABCD中,E是BC边上一点,以E为圆心、EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,求sin∠EAB的值。
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
