人教版数学七年级下册 8.3.1 实际问题与二元一次方程组 第1课时 课件(共29张PPT)
文档属性
| 名称 | 人教版数学七年级下册 8.3.1 实际问题与二元一次方程组 第1课时 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
8.3.1 利用二元一次方程组
解决实际问题
第八章 二元一次方程组
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.
2.学会利用二元一次方程组解决几何、行程问题.
重点难点:
1.会运用二元一次方程组解决一些实际生活中的应用问题,体会数学建模思想.
2.能根据题目中的已知量与未知量的联系正确设出未知数,列出方程组并求解.
学习目标:
情景导入
前面我们结合实际问题,讨论了用方程组表示问题中的等量关系以及如何解方程组.本节课我们继续探究如何用二元一次方程组解决实际问题.
知识精讲
知识点一 列二元一次方程组解答较简单问题
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗?
问题1:题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2:题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用
饲料为xkg和ykg,
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组:x= ,
y= .
20
5
剧情发展:随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人,则:
+ = 42,
+ = 20.
8x
5y
4x
2y
解得:
x =4
y = 2
答:李大叔应聘请甲种饲养员4人,乙种饲养员2人.
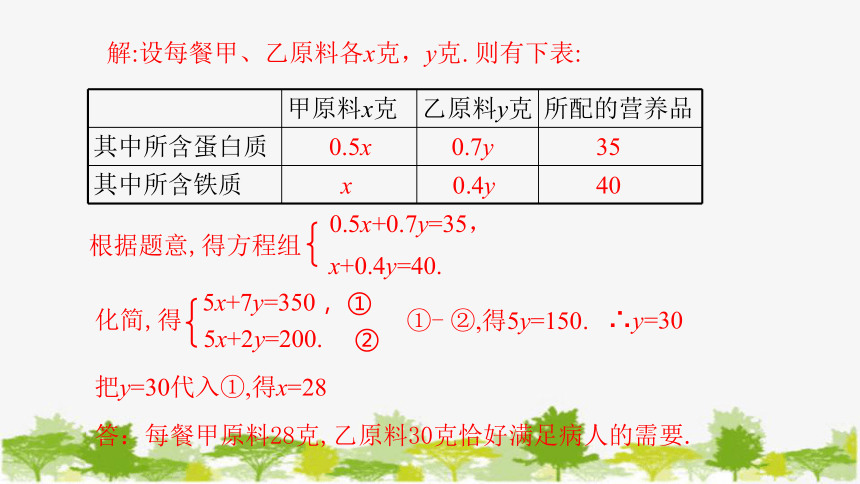
例1 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要
解:设每餐甲、乙原料各x克,y克. 则有下表:
甲原料x克 乙原料y克 所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
根据题意,得方程组
化简,得
①- ②,得5y=150.
∴y=30
把y=30代入①,得x=28
答:每餐甲原料28克,乙原料30克恰好满足病人的需要.
0.5x+0.7y=35,
x+0.4y=40.
5x+7y=350, ①
5x+2y=200. ②
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用_______表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用_________法或_________法解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元
针对练习
1某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场,平几场?
解:设市第二中学足球队胜x场,平y场.依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场,平3场.
x
知识点二 列二元一次方程组解答几何问题
据统计资料,甲、乙两种作物的单位面积产量的比1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
A
D
C
B
这里研究的实际上是什么问题.
竖着画,把长分成两段,则宽不变
横着画,把宽分成两段,则长不变
长方形的面积分割
我们可以画出示意图来帮助分析
把一个长方形分成两个小长方形有哪些分割方式?
方法1
方法2
竖着画,把长分成两段,则宽不变
A
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
设AE=xm,BE=ym.
先求出两种作物的面积
SAEFD=100x
SEFCB=100y
再写出两种作物的总产量
甲:100x×1
乙:100y×2
则列方程为
100x:200y=3:4
总产量=
1 : 2
D
C
F
x
y
200m
100m
则列方程为
x+y=200
单位面积产量×面积
方法1
A
D
C
F
B
E
根据题意列方程组为
100x:200y=3:4
x
y
200m
100m
x+y=200
解得
x=120
y=80
甲种
作物
乙种
作物
解:
过点E作EF⊥AB,交CD于点F.
设AE=xm,BE=ym.
答:将这块土地分为长120m,宽100m和长100m,宽80m的
两个小长方形分别种植甲、乙两种作物.
竖着画,把长分成两段,则宽不变
方法1
A
D
C
B
E
x
y
F
x+y=100
乙种作物
甲种作物
解:过点E作EF⊥AD,交BC于点F.
设DE=xm,AE=ym.
200x:400y=3:4
200y
200x
x=60
y=40
解得
根据题意列方程组为
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
横着画,把宽分成两段,则长不变
方法2
例2 某校现有校舍20000m2计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2 )
由题意得
解得
答:应该拆除2000m2旧校舍,建造8000m2新校舍.
解:设应拆除旧校舍xm2,建造新校舍ym2
拆
20000m2
新建
解:设小长方形地砖的长为x, 宽为y,
由题意,得
针对练习
60
x+y=60
x=3y
解此方程组得
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
1. 8块相同的小长方形地砖拼成一个大长方形,每小长方形地砖的长和宽分别是多少 (单位cm)
知识点三 列二元一次方程组解答行程问题
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
分析:小华到学校的路分成两段,一段为平路,
一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡路的时间=________,
走上坡路的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡路长y m.
解方程组,得
所以,小明家到学校的距离为700m.
方法二(间接设元法)
平路 距离 坡路距离
上学
放学
解:设小华下坡路所花时间为xmin,
上坡路所花时间为ymin.
解方程组,得
所以,小明家到学校的距离为700m.
故 平路距离:60×(10-5)=300(m)
坡路距离:80×5=400(m)
例3 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
针对练习
1.巴广高速公路在5月10日正式通车,从巴中到广元全长约126 km,一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行6 km,设小汽车和货车的速度分别为x km/h、y km/h,则下列方程组正确的是( )
A. B.
C. D.
D
当堂检测
1.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )
A. B.
C. D.
D
2.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为( )
B.
C. D.
D
D
3.我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
4 甲、乙两人都从A地到B地,甲步行,乙骑自行车,如果甲先走6千米乙再动身,则乙走 小时后恰好与甲同时到达B地;如果甲先走1小时,那么乙用 小时可追上甲,求两人的速度.
解:设甲的速度为x千米/时,乙的速度为y千米/时,则
答:甲的速度为4千米/时,乙的速度为12千米/时.
课堂小结
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据2个等量关系列出方程组
解方程组:代入法;加减法
检验作答
几何问题
8.3.1 利用二元一次方程组
解决实际问题
第八章 二元一次方程组
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.
2.学会利用二元一次方程组解决几何、行程问题.
重点难点:
1.会运用二元一次方程组解决一些实际生活中的应用问题,体会数学建模思想.
2.能根据题目中的已知量与未知量的联系正确设出未知数,列出方程组并求解.
学习目标:
情景导入
前面我们结合实际问题,讨论了用方程组表示问题中的等量关系以及如何解方程组.本节课我们继续探究如何用二元一次方程组解决实际问题.
知识精讲
知识点一 列二元一次方程组解答较简单问题
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗?
问题1:题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2:题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用
饲料为xkg和ykg,
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组:x= ,
y= .
20
5
剧情发展:随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人,则:
+ = 42,
+ = 20.
8x
5y
4x
2y
解得:
x =4
y = 2
答:李大叔应聘请甲种饲养员4人,乙种饲养员2人.
例1 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要
解:设每餐甲、乙原料各x克,y克. 则有下表:
甲原料x克 乙原料y克 所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
根据题意,得方程组
化简,得
①- ②,得5y=150.
∴y=30
把y=30代入①,得x=28
答:每餐甲原料28克,乙原料30克恰好满足病人的需要.
0.5x+0.7y=35,
x+0.4y=40.
5x+7y=350, ①
5x+2y=200. ②
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用_______表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用_________法或_________法解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元
针对练习
1某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场,平几场?
解:设市第二中学足球队胜x场,平y场.依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场,平3场.
x
知识点二 列二元一次方程组解答几何问题
据统计资料,甲、乙两种作物的单位面积产量的比1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
A
D
C
B
这里研究的实际上是什么问题.
竖着画,把长分成两段,则宽不变
横着画,把宽分成两段,则长不变
长方形的面积分割
我们可以画出示意图来帮助分析
把一个长方形分成两个小长方形有哪些分割方式?
方法1
方法2
竖着画,把长分成两段,则宽不变
A
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
设AE=xm,BE=ym.
先求出两种作物的面积
SAEFD=100x
SEFCB=100y
再写出两种作物的总产量
甲:100x×1
乙:100y×2
则列方程为
100x:200y=3:4
总产量=
1 : 2
D
C
F
x
y
200m
100m
则列方程为
x+y=200
单位面积产量×面积
方法1
A
D
C
F
B
E
根据题意列方程组为
100x:200y=3:4
x
y
200m
100m
x+y=200
解得
x=120
y=80
甲种
作物
乙种
作物
解:
过点E作EF⊥AB,交CD于点F.
设AE=xm,BE=ym.
答:将这块土地分为长120m,宽100m和长100m,宽80m的
两个小长方形分别种植甲、乙两种作物.
竖着画,把长分成两段,则宽不变
方法1
A
D
C
B
E
x
y
F
x+y=100
乙种作物
甲种作物
解:过点E作EF⊥AD,交BC于点F.
设DE=xm,AE=ym.
200x:400y=3:4
200y
200x
x=60
y=40
解得
根据题意列方程组为
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
横着画,把宽分成两段,则长不变
方法2
例2 某校现有校舍20000m2计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2 )
由题意得
解得
答:应该拆除2000m2旧校舍,建造8000m2新校舍.
解:设应拆除旧校舍xm2,建造新校舍ym2
拆
20000m2
新建
解:设小长方形地砖的长为x, 宽为y,
由题意,得
针对练习
60
x+y=60
x=3y
解此方程组得
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
1. 8块相同的小长方形地砖拼成一个大长方形,每小长方形地砖的长和宽分别是多少 (单位cm)
知识点三 列二元一次方程组解答行程问题
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
分析:小华到学校的路分成两段,一段为平路,
一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡路的时间=________,
走上坡路的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡路长y m.
解方程组,得
所以,小明家到学校的距离为700m.
方法二(间接设元法)
平路 距离 坡路距离
上学
放学
解:设小华下坡路所花时间为xmin,
上坡路所花时间为ymin.
解方程组,得
所以,小明家到学校的距离为700m.
故 平路距离:60×(10-5)=300(m)
坡路距离:80×5=400(m)
例3 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
针对练习
1.巴广高速公路在5月10日正式通车,从巴中到广元全长约126 km,一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行6 km,设小汽车和货车的速度分别为x km/h、y km/h,则下列方程组正确的是( )
A. B.
C. D.
D
当堂检测
1.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )
A. B.
C. D.
D
2.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为( )
B.
C. D.
D
D
3.我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
4 甲、乙两人都从A地到B地,甲步行,乙骑自行车,如果甲先走6千米乙再动身,则乙走 小时后恰好与甲同时到达B地;如果甲先走1小时,那么乙用 小时可追上甲,求两人的速度.
解:设甲的速度为x千米/时,乙的速度为y千米/时,则
答:甲的速度为4千米/时,乙的速度为12千米/时.
课堂小结
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据2个等量关系列出方程组
解方程组:代入法;加减法
检验作答
几何问题
