2021-2022学年华东师大版数学九年级上册第24章解直角三角形单元检测(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级上册第24章解直角三角形单元检测(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 107.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览





文档简介
《第24章 解直角三角形》单元测试
一、选择题(每题3分,共24分)
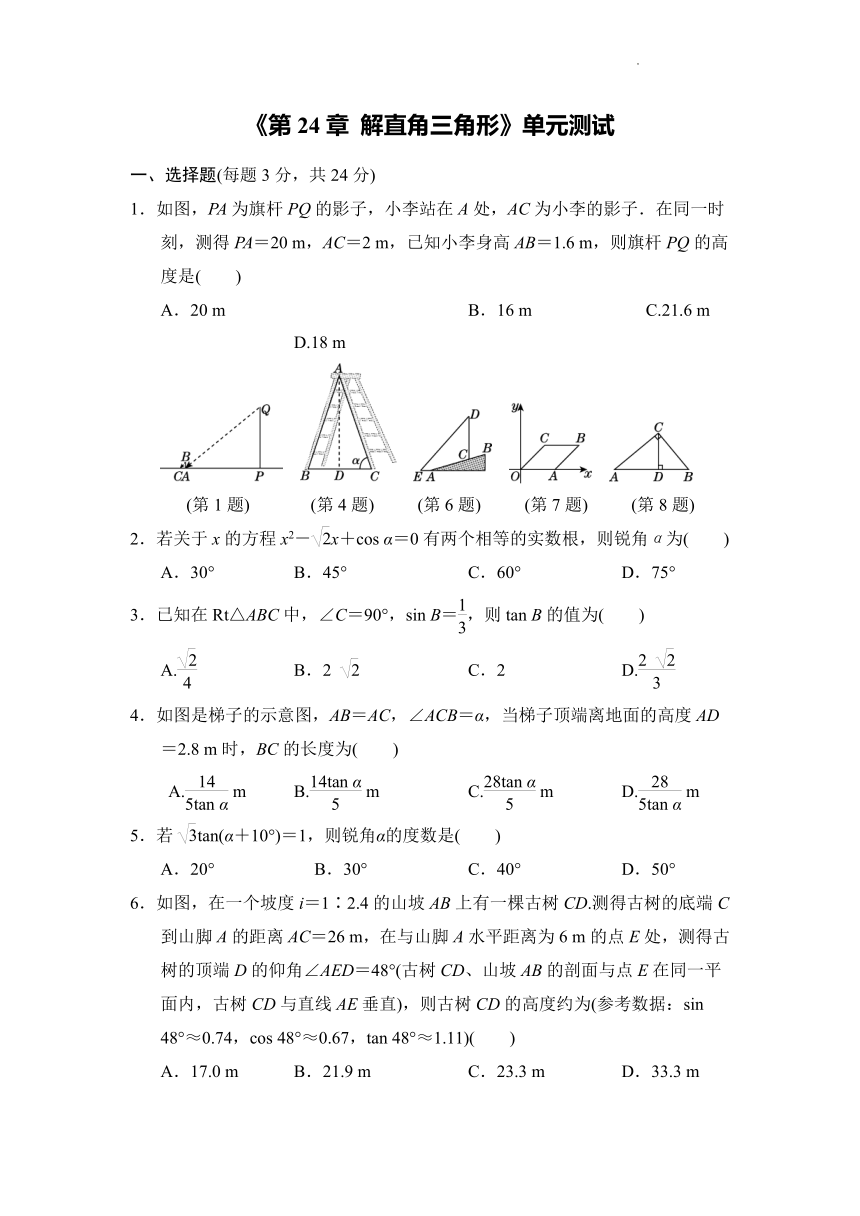
1.如图,PA为旗杆PQ的影子,小李站在A处,AC为小李的影子.在同一时刻,测得PA=20 m,AC=2 m,已知小李身高AB=1.6 m,则旗杆PQ的高度是( )
A.20 m B.16 m C.21.6 m D.18 m
(第1题) (第4题) (第6题) (第7题) (第8题)
2.若关于x的方程x2-x+cos α=0有两个相等的实数根,则锐角α为( )
A.30° B.45° C.60° D.75°
3.已知在Rt△ABC中,∠C=90°,sin B=,则tan B的值为( )
A. B.2 C.2 D.
4.如图是梯子的示意图,AB=AC,∠ACB=α,当梯子顶端离地面的高度AD=2.8 m时,BC的长度为( )
A. m B. m C. m D. m
5.若tan(α+10°)=1,则锐角α的度数是( )
A.20° B.30° C.40° D.50°
6.如图,在一个坡度i=1∶2.4的山坡AB上有一棵古树CD.测得古树的底端C到山脚A的距离AC=26 m,在与山脚A水平距离为6 m的点E处,测得古树的顶端D的仰角∠AED=48°(古树CD、山坡AB的剖面与点E在同一平面内,古树CD与直线AE垂直),则古树CD的高度约为(参考数据:sin 48°≈0.74,cos 48°≈0.67,tan 48°≈1.11)( )
A.17.0 m B.21.9 m C.23.3 m D.33.3 m
7.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OA=,则点C的坐标为( )
A.(,1) B.(1,1)
C.(1,) D.( +1,1)
8.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD的值为( )
A. B. C. D.
二、填空题(每题3分,共18分)
9.等腰三角形底边长10 cm,周长为36 cm,则底角的余弦值为________.
10.小红沿着坡度i=1?的斜面向上走了48 m,则小红沿着垂直方向升高了________ m.
11.如图,在由边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则cos∠APD=________.
(第11题) (第12题) (第14题)
12.如图,在△ABC中,sin B=,tan C=2,AB=3,则AC的长为____________.
13.计算: -4cos 45°-+3tan 30°的结果为________.
14.如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3 ,则BD的长度为________.
三、解答题(第15题16分,第16~19题每题8分,其余每题10分,共78分)
15.计算:
(1)4sin 30°-cos 45°-tan 30°+2sin 60°;
(2);
(3)2sin 45°- tan 30°- ;
(4)(tan 60°)-1×-+8×0.125.
16.已知△ABC中的∠A与∠B满足(1-tan A)2+=0,试判断△ABC的形状.
17.如图,△ABC中,∠ACB=90°,点D是边BC上一点,连结AD,DE⊥AB于点E,点F是线段AD的中点,连结EF,CF.
(第17题)
(1)求证:EF=CF;
(2)若∠BAC=30°,连结EC,试判断△EFC 的形状,并说明理由.
18.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,测得地面上的影长为8 m,坡面上的影长为4 m,已知斜坡的坡角为30°.同一时刻,一根长为1 m且垂直于地面放置的标杆在地面上的影长为2 m,求树的高度.
(第18题)
19.如图,一艘海船以5 n mile/h的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2 h后海船行驶到C处,此时灯塔B在海船的北偏西45°方向,求灯塔B到C处的距离.
(第19题)
20.如图,为了测量一栋楼AB的高度,小明在D处用高为1 m的测角仪CD测得楼顶A的仰角为30°,向楼的方向前进20 m到达E处,又测得楼顶A的仰角为60°,求这栋楼AB的高度.
(第20题)
21.定义:在△ABC中,我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A==.请解答下列问题:
已知在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ,则∠A=________;
(3)若∠A是锐角,探究thi A与sin A的数量关系.
22. 一种手机支架是由托板、支撑板和底座构成的,手机放置在托板上,如图是支架的侧面结构示意图.托板AB=120 mm,支撑板CD=80 mm,底座DE=90 mm.托板AB与支撑板顶端C相连,CB=40 mm,AB可绕点C转动,CD可绕点D转动.
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上,求CD旋转的角度.(结果保留到小数点后一位,参考数据:≈1.732,sin 40°≈0.643,cos 40°≈0.766,tan 40°≈0.839,sin 26.6°≈0.448,cos 26.6°≈0.894,tan 26.6°≈0.501)
(第22题)
答案
一、1.B 2.C 3.A 4.D 5.A
6.C 7.B 8.A
二、9. 10.24 11.
12.
13.1 14.2
三、15.解:(1)原式=4×-×-×+2×=2-1-1+=.
(2)原式===
=3-2 .
(3)原式=2×-×-|1-|
=-1-(-1)=-1- +1=0.
(4)原式=()-1×-+8×0.125
=×-+1=-+1=1.
16.解:∵(1-tan A)2+=0,
∴1-tan A=0,sin B-=0,即tan A=1,sin B=,
∴∠A=45°,∠B=60°,
∴∠C=180°-45°-60°=75°,∴△ABC是锐角三角形.
17.(1)证明:∵DE⊥AB,∴∠DEA=90°.
∵点F是线段AD的中点,∠DEA=90°,∠ACD=90°,
∴EF=AD,CF=AD,∴EF=CF.
(2)解:△EFC是等边三角形. 理由如下:
由(1)可得EF=AF=CF,
∴∠FEA=∠FAE,∠FCA=∠FAC,
∴∠EFC=2∠BAC=60°.
又∵EF=CF,∴△EFC是等边三角形.
18.解:如图,延长AC交BF的延长线于点D,
作CE⊥BD于点E.
在Rt△CFE中,∠CFE=30°,CF=4 m,
∴CE=2 m,EF=4cos 30°=4×=2 (m).
∵同一时刻,一根长为1 m且垂直于地面放置的标杆在地面上的影长为2 m,
∴CE∶DE=1∶2,AB∶BD=1∶2,∴DE=4 m,
∴BD=BF+EF+ED=8+2 +4=12+2 (m).
∴AB=BD=×(12+2 )=+6(m).
答:树的高度为(+6)m.
(第18题)
19.解:过点B作BD⊥AC于点D.
易得∠DAB=90°-60°=30°,∠DCB=90°-45°=45°.
设BD=x n mile,
在Rt△ABD中,AD== x(n mile),
在Rt△BDC中,BD=DC=x n mile,BC= x n mile.
∵AC=5×2=10(n mile),∴x+x=10,
解得x=5(-1).
∴BC=×5(-1)=5(-)(n mile).
答:灯塔B到C处的距离为5(-) n mile.
20.解:设AG=x m,
由题意,得BG=CD=1 m.
在Rt△AFG中,∠AFG=60°,
∴tan∠AFG= =,∴FG= x m.
在Rt△ACG中,∠ACG=30°,
∴tan∠ACG= =,∴CG=x m.
又∵CG-FG=20 m,∴x-x=20,
∴x=10 ,∴AB=AG+BG=(10 +1)m.
答:这栋楼AB的高度为(10 +1)m.
21.解:(1)如图,在△ABC中,∠C=30°,∠A=45°.过点B作BH⊥AC,垂足为H.
在Rt△BHC中,sin C==,即BC=2BH.
在Rt△BHA中,sin A==,即AB=BH.
∴thi A==.
(2)60°或120°
(3)如图,在△ABC中,∠C=30°,thi A=.
在Rt△BHA中,sin A=.
在Rt△BHC中,sin C==,即BC=2BH.
∴thi A=,∴thi A=2sin A.
(第21题)
22.解:(1)如图①,过点A作AM⊥DE,交ED的延长线于点M,过点C作CF⊥AM于点F,作CN⊥DE于点N,可得矩形CFMN,
由题意可得AC=80 mm,
在Rt△CDN中,CN=CD·sin∠CDE=80×=40 (mm),
∠DCN=90°-60°=30°.
又∵∠DCB=80°, ∴∠BCN=50°,∴∠A=50°,
∴∠ACF=180°-90°-50°=40°.
在Rt△AFC中,AF=AC·sin 40°≈80×0.643=51.44(mm),
∴AM=AF+FM=AF+CN≈51.44+40 ≈120.7 (mm).
∴点A到直线DE的距离约为120.7 mm.
(2)旋转后,如图②所示,根据题意可知∠DCB=80°+10°=90°.
在Rt△BCD中,CD=80 mm,BC=40 mm,
∴tan D===0.5,∴∠D≈26.6°,
∴CD旋转的角度约为60°-26.6°=33.4°.
(第22题)
一、选择题(每题3分,共24分)
1.如图,PA为旗杆PQ的影子,小李站在A处,AC为小李的影子.在同一时刻,测得PA=20 m,AC=2 m,已知小李身高AB=1.6 m,则旗杆PQ的高度是( )
A.20 m B.16 m C.21.6 m D.18 m
(第1题) (第4题) (第6题) (第7题) (第8题)
2.若关于x的方程x2-x+cos α=0有两个相等的实数根,则锐角α为( )
A.30° B.45° C.60° D.75°
3.已知在Rt△ABC中,∠C=90°,sin B=,则tan B的值为( )
A. B.2 C.2 D.
4.如图是梯子的示意图,AB=AC,∠ACB=α,当梯子顶端离地面的高度AD=2.8 m时,BC的长度为( )
A. m B. m C. m D. m
5.若tan(α+10°)=1,则锐角α的度数是( )
A.20° B.30° C.40° D.50°
6.如图,在一个坡度i=1∶2.4的山坡AB上有一棵古树CD.测得古树的底端C到山脚A的距离AC=26 m,在与山脚A水平距离为6 m的点E处,测得古树的顶端D的仰角∠AED=48°(古树CD、山坡AB的剖面与点E在同一平面内,古树CD与直线AE垂直),则古树CD的高度约为(参考数据:sin 48°≈0.74,cos 48°≈0.67,tan 48°≈1.11)( )
A.17.0 m B.21.9 m C.23.3 m D.33.3 m
7.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OA=,则点C的坐标为( )
A.(,1) B.(1,1)
C.(1,) D.( +1,1)
8.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD的值为( )
A. B. C. D.
二、填空题(每题3分,共18分)
9.等腰三角形底边长10 cm,周长为36 cm,则底角的余弦值为________.
10.小红沿着坡度i=1?的斜面向上走了48 m,则小红沿着垂直方向升高了________ m.
11.如图,在由边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则cos∠APD=________.
(第11题) (第12题) (第14题)
12.如图,在△ABC中,sin B=,tan C=2,AB=3,则AC的长为____________.
13.计算: -4cos 45°-+3tan 30°的结果为________.
14.如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3 ,则BD的长度为________.
三、解答题(第15题16分,第16~19题每题8分,其余每题10分,共78分)
15.计算:
(1)4sin 30°-cos 45°-tan 30°+2sin 60°;
(2);
(3)2sin 45°- tan 30°- ;
(4)(tan 60°)-1×-+8×0.125.
16.已知△ABC中的∠A与∠B满足(1-tan A)2+=0,试判断△ABC的形状.
17.如图,△ABC中,∠ACB=90°,点D是边BC上一点,连结AD,DE⊥AB于点E,点F是线段AD的中点,连结EF,CF.
(第17题)
(1)求证:EF=CF;
(2)若∠BAC=30°,连结EC,试判断△EFC 的形状,并说明理由.
18.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,测得地面上的影长为8 m,坡面上的影长为4 m,已知斜坡的坡角为30°.同一时刻,一根长为1 m且垂直于地面放置的标杆在地面上的影长为2 m,求树的高度.
(第18题)
19.如图,一艘海船以5 n mile/h的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2 h后海船行驶到C处,此时灯塔B在海船的北偏西45°方向,求灯塔B到C处的距离.
(第19题)
20.如图,为了测量一栋楼AB的高度,小明在D处用高为1 m的测角仪CD测得楼顶A的仰角为30°,向楼的方向前进20 m到达E处,又测得楼顶A的仰角为60°,求这栋楼AB的高度.
(第20题)
21.定义:在△ABC中,我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A==.请解答下列问题:
已知在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ,则∠A=________;
(3)若∠A是锐角,探究thi A与sin A的数量关系.
22. 一种手机支架是由托板、支撑板和底座构成的,手机放置在托板上,如图是支架的侧面结构示意图.托板AB=120 mm,支撑板CD=80 mm,底座DE=90 mm.托板AB与支撑板顶端C相连,CB=40 mm,AB可绕点C转动,CD可绕点D转动.
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上,求CD旋转的角度.(结果保留到小数点后一位,参考数据:≈1.732,sin 40°≈0.643,cos 40°≈0.766,tan 40°≈0.839,sin 26.6°≈0.448,cos 26.6°≈0.894,tan 26.6°≈0.501)
(第22题)
答案
一、1.B 2.C 3.A 4.D 5.A
6.C 7.B 8.A
二、9. 10.24 11.
12.
13.1 14.2
三、15.解:(1)原式=4×-×-×+2×=2-1-1+=.
(2)原式===
=3-2 .
(3)原式=2×-×-|1-|
=-1-(-1)=-1- +1=0.
(4)原式=()-1×-+8×0.125
=×-+1=-+1=1.
16.解:∵(1-tan A)2+=0,
∴1-tan A=0,sin B-=0,即tan A=1,sin B=,
∴∠A=45°,∠B=60°,
∴∠C=180°-45°-60°=75°,∴△ABC是锐角三角形.
17.(1)证明:∵DE⊥AB,∴∠DEA=90°.
∵点F是线段AD的中点,∠DEA=90°,∠ACD=90°,
∴EF=AD,CF=AD,∴EF=CF.
(2)解:△EFC是等边三角形. 理由如下:
由(1)可得EF=AF=CF,
∴∠FEA=∠FAE,∠FCA=∠FAC,
∴∠EFC=2∠BAC=60°.
又∵EF=CF,∴△EFC是等边三角形.
18.解:如图,延长AC交BF的延长线于点D,
作CE⊥BD于点E.
在Rt△CFE中,∠CFE=30°,CF=4 m,
∴CE=2 m,EF=4cos 30°=4×=2 (m).
∵同一时刻,一根长为1 m且垂直于地面放置的标杆在地面上的影长为2 m,
∴CE∶DE=1∶2,AB∶BD=1∶2,∴DE=4 m,
∴BD=BF+EF+ED=8+2 +4=12+2 (m).
∴AB=BD=×(12+2 )=+6(m).
答:树的高度为(+6)m.
(第18题)
19.解:过点B作BD⊥AC于点D.
易得∠DAB=90°-60°=30°,∠DCB=90°-45°=45°.
设BD=x n mile,
在Rt△ABD中,AD== x(n mile),
在Rt△BDC中,BD=DC=x n mile,BC= x n mile.
∵AC=5×2=10(n mile),∴x+x=10,
解得x=5(-1).
∴BC=×5(-1)=5(-)(n mile).
答:灯塔B到C处的距离为5(-) n mile.
20.解:设AG=x m,
由题意,得BG=CD=1 m.
在Rt△AFG中,∠AFG=60°,
∴tan∠AFG= =,∴FG= x m.
在Rt△ACG中,∠ACG=30°,
∴tan∠ACG= =,∴CG=x m.
又∵CG-FG=20 m,∴x-x=20,
∴x=10 ,∴AB=AG+BG=(10 +1)m.
答:这栋楼AB的高度为(10 +1)m.
21.解:(1)如图,在△ABC中,∠C=30°,∠A=45°.过点B作BH⊥AC,垂足为H.
在Rt△BHC中,sin C==,即BC=2BH.
在Rt△BHA中,sin A==,即AB=BH.
∴thi A==.
(2)60°或120°
(3)如图,在△ABC中,∠C=30°,thi A=.
在Rt△BHA中,sin A=.
在Rt△BHC中,sin C==,即BC=2BH.
∴thi A=,∴thi A=2sin A.
(第21题)
22.解:(1)如图①,过点A作AM⊥DE,交ED的延长线于点M,过点C作CF⊥AM于点F,作CN⊥DE于点N,可得矩形CFMN,
由题意可得AC=80 mm,
在Rt△CDN中,CN=CD·sin∠CDE=80×=40 (mm),
∠DCN=90°-60°=30°.
又∵∠DCB=80°, ∴∠BCN=50°,∴∠A=50°,
∴∠ACF=180°-90°-50°=40°.
在Rt△AFC中,AF=AC·sin 40°≈80×0.643=51.44(mm),
∴AM=AF+FM=AF+CN≈51.44+40 ≈120.7 (mm).
∴点A到直线DE的距离约为120.7 mm.
(2)旋转后,如图②所示,根据题意可知∠DCB=80°+10°=90°.
在Rt△BCD中,CD=80 mm,BC=40 mm,
∴tan D===0.5,∴∠D≈26.6°,
∴CD旋转的角度约为60°-26.6°=33.4°.
(第22题)
