2021-2022学年北师大版九年级数学下册2.4二次函数的应用同步练习(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.4二次函数的应用同步练习(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 142.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 14:57:45 | ||
图片预览


文档简介
北师大版九年级数学下册第一章2.4二次函数的应用 同步测试
一.选择题
如图所示的抛物线的解析式是 ( )
y=x2-x+2 B.y=-x2-x+2 C.y=x2+x+2 D.y=-x2+x+2
2.为了测量某沙漠地区的温度变化情况,从某时刻开始记录了12个小时的温度,记时间为t(单位:h),温度为y(单位:℃).当4≤t≤8时,y与t的函数关系是y=﹣t2+10t+11,则4≤t≤8时该地区的最高温度是( )
A.11℃ B.27℃ C.35℃ D.36℃
3.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.4 m D.4m
4.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825 B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900 D.y=﹣2(x﹣65)2+2000
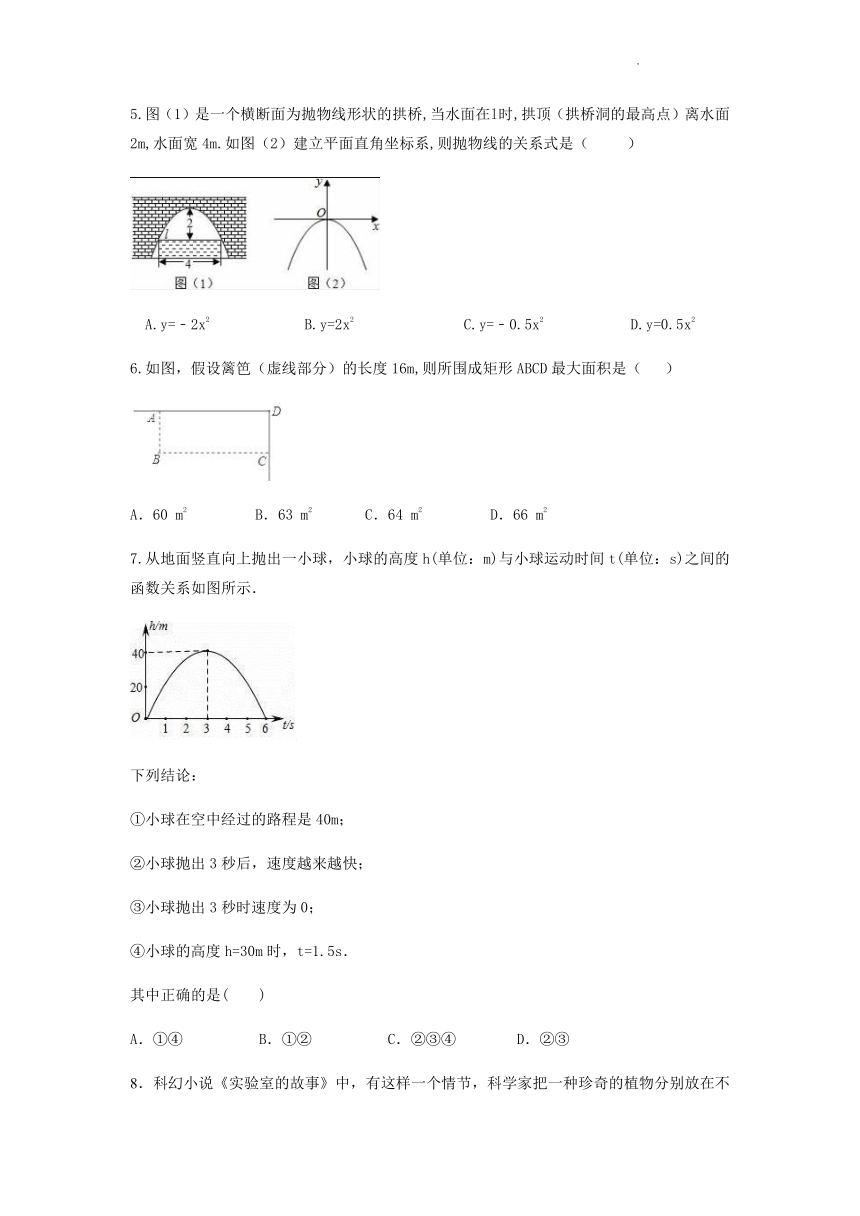
5.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A.y=﹣2x2 B.y=2x2 C.y=﹣0.5x2 D.y=0.5x2
6.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD最大面积是( )
A.60 m2 B.63 m2 C.64 m2 D.66 m2
7.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.
下列结论:
①小球在空中经过的路程是40m;
②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;
④小球的高度h=30m时,t=1.5s.
其中正确的是( )
A.①④ B.①② C.②③④ D.②③
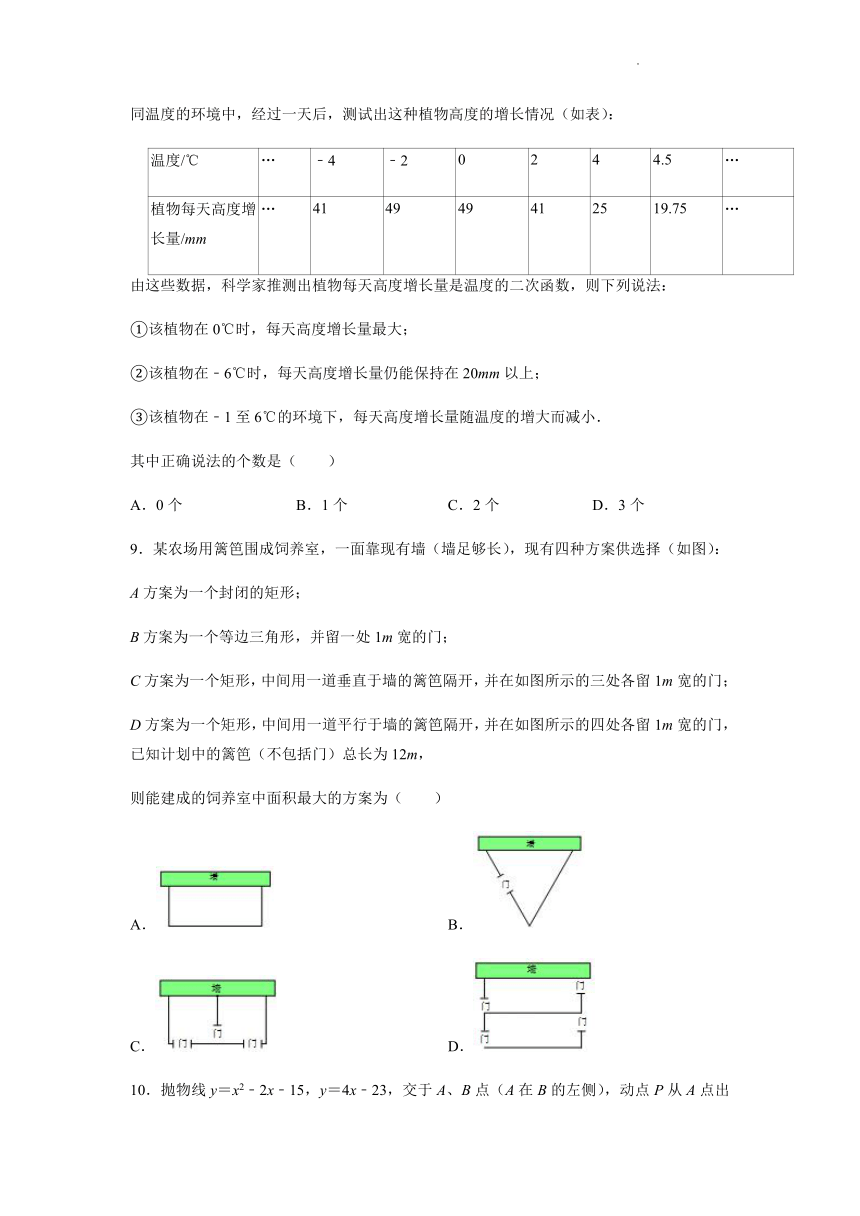
8.科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表):
温度/℃ … ﹣4 ﹣2 0 2 4 4.5 …
植物每天高度增长量/mm … 41 49 49 41 25 19.75 …
由这些数据,科学家推测出植物每天高度增长量是温度的二次函数,则下列说法:
①该植物在0℃时,每天高度增长量最大;
②该植物在﹣6℃时,每天高度增长量仍能保持在20mm以上;
③该植物在﹣1至6℃的环境下,每天高度增长量随温度的增大而减小.
其中正确说法的个数是( )
A.0个 B.1个 C.2个 D.3个
9.某农场用篱笆围成饲养室,一面靠现有墙(墙足够长),现有四种方案供选择(如图):
A方案为一个封闭的矩形;
B方案为一个等边三角形,并留一处1m宽的门;
C方案为一个矩形,中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留1m宽的门;
D方案为一个矩形,中间用一道平行于墙的篱笆隔开,并在如图所示的四处各留1m宽的门,已知计划中的篱笆(不包括门)总长为12m,
则能建成的饲养室中面积最大的方案为( )
A. B.
C. D.
10.抛物线y=x2﹣2x﹣15,y=4x﹣23,交于A、B点(A在B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E再到达x轴上的某点F,最后运动到点B.若使点P动的总路径最短,则点P运动的总路径的长为( )
A.10 B.7 C.5 D.8
二.填空题
11抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为l,则b的值是 .
12.某商店将进货价为70元/个的商品按零售价100元/个出售时,每天能卖出20个,若零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价 元.
13.一名男生参加抛实心球测试,已知球的高度y(m)与水平距离x(m)之间的关系是,则这名男生抛实心球的成绩是 m.
14.学校准备建一个矩形花圃,其中一边靠墙,另外三边用周长为30米的篱笆围成,已知墙长为18米,设花圃垂直于墙的一边长为x米,花圃的面积为y平方米,写出y与x的函数关系式,并写出自变量x的取值范围 .
15.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为y=﹣x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.
16.某商品进货单价为30元,按40元一个销售能卖40个;若销售单价每涨1元,则销量减少1个.设涨价x元,利润为y元,则y与x的函数关系为 .
三.解答题
17.某商店销售一种进价50元/件的商品,经市场调查发现:该商品的每天销售量y(件)是售价x(元/件)的一次函数,其售价、销售量的二组对应值如下表:
售价x(元/件) 55 65
销售量y(件/天) 90 70
(1)若某天销售利润为800元,求该天的售价为多少元/件.
(2)由于某种原因,该商品进价提高了a元/件(a>0),商店售价不低于进价,物价部门规定该商品售价不得超过70元件,该商店在今后的销售中,每天能获得的销售最大利润是960元,求a的值.
18.喷洒酒精能有效杀灭“新型冠状肺炎”病毒.根据实验知道喷洒酒精在教室内空气中的浓度y(单位:mg/m3)与时间x(单位:h)的函数表达式为y=.其大致图象如图所示.请根据以上信息解答下列问题:
(1)试确定点A的坐标;
(2)根据经验,当教室空气中的药物浓度不低于1mg/m3时,杀灭“新型冠状肺炎”病毒的效果最佳,请通过计算说明单次喷洒酒精杀灭“新型冠状肺炎”病毒的效果处于最佳状态的时间为多少小时?
19.如图,在平面直角坐标系中,直线y=kx+1与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2﹣(6a﹣2)x+b与直线AC交于另一点B(4,3).
(1)求抛物线的表达式;
(2)已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求出m的值.
答案提示
1.D.2.D.3.D.4.D.5.C.6.C.7.D.8.C.9.C.10.A.
11.-3. 12.5. 13. 10. 14.y=﹣2x2+30x(6≤x<15).
15.8.
16.y=﹣x2+30x+400(0≤x≤40),
17.解:(1)依题意设y=kx+b,
则有,
解得:,
所以y=﹣2x+200,
若某天销售利润为800元,
则(x﹣50)(﹣2x+200)=800,
解得:x1=60,x2=90,
该天的售价为60元或者90元;
(2)设总利润为w,根据题意得,
w=(x﹣50﹣a)(﹣2x+200)
=﹣2x2+(300+2a)x﹣10000﹣200a
∵a>0,
∴对称轴x=>75,
∵﹣2<0,
∴抛物线的开口向下,
∵x≤70,
∴w随x的增大而增大,
当x=70时,w最大=960,
即960=﹣2×702+(300+2a)×70﹣10000﹣200a,
解得:a=4.
18.解:(1)由题意可得A为函数y=2x与y=﹣x2+6x﹣4的交点,
所以2x=﹣x2+6x﹣4,
解得x1=x2=2,代入y=2x得y=4,
可得A(2,4).
(2)当教室空气中的药物浓度不低于1mg/m3时,杀灭“新型冠状肺炎”病毒的效果最佳,
由(1)得m=2,
当0<x<2时,
令y=1,
2x=1,
x=;
当x≥2时,
令y=1,
﹣x2+6x﹣4=1
整理得x2﹣6x+5=0
解得x1=1(不合题意,舍去),x2=5,
所以x=5,
所以单次喷洒酒精杀灭“新型冠状肺炎”病毒的效果处于最佳状态的时间为(5﹣)=4.5小时.
19.解:(1)点C的坐标为(0,1),b=1,
将点B坐标代入代入一次函数表达式得:3=4k+1,解得:k=,
则一次函数表达式为:y=x+1,则点A坐标为(﹣2,0),
把点C.B坐标代入二次函数表达式得:3=a×42﹣4(6a﹣2)+1,解得:a=,
则二次函数表达式为:y=x2﹣x+1;
(2)①如下图,当∠AQB=90°时,
△ABQ与△AOC相似,m=4,
②当∠ABQ=90°时,△ABQ与△AOC相似,
AB==3,cos∠BAO==,
则AQ==,
则m=﹣2=,
即:m的值为4或.
一.选择题
如图所示的抛物线的解析式是 ( )
y=x2-x+2 B.y=-x2-x+2 C.y=x2+x+2 D.y=-x2+x+2
2.为了测量某沙漠地区的温度变化情况,从某时刻开始记录了12个小时的温度,记时间为t(单位:h),温度为y(单位:℃).当4≤t≤8时,y与t的函数关系是y=﹣t2+10t+11,则4≤t≤8时该地区的最高温度是( )
A.11℃ B.27℃ C.35℃ D.36℃
3.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.4 m D.4m
4.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825 B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900 D.y=﹣2(x﹣65)2+2000
5.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A.y=﹣2x2 B.y=2x2 C.y=﹣0.5x2 D.y=0.5x2
6.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD最大面积是( )
A.60 m2 B.63 m2 C.64 m2 D.66 m2
7.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.
下列结论:
①小球在空中经过的路程是40m;
②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;
④小球的高度h=30m时,t=1.5s.
其中正确的是( )
A.①④ B.①② C.②③④ D.②③
8.科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表):
温度/℃ … ﹣4 ﹣2 0 2 4 4.5 …
植物每天高度增长量/mm … 41 49 49 41 25 19.75 …
由这些数据,科学家推测出植物每天高度增长量是温度的二次函数,则下列说法:
①该植物在0℃时,每天高度增长量最大;
②该植物在﹣6℃时,每天高度增长量仍能保持在20mm以上;
③该植物在﹣1至6℃的环境下,每天高度增长量随温度的增大而减小.
其中正确说法的个数是( )
A.0个 B.1个 C.2个 D.3个
9.某农场用篱笆围成饲养室,一面靠现有墙(墙足够长),现有四种方案供选择(如图):
A方案为一个封闭的矩形;
B方案为一个等边三角形,并留一处1m宽的门;
C方案为一个矩形,中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留1m宽的门;
D方案为一个矩形,中间用一道平行于墙的篱笆隔开,并在如图所示的四处各留1m宽的门,已知计划中的篱笆(不包括门)总长为12m,
则能建成的饲养室中面积最大的方案为( )
A. B.
C. D.
10.抛物线y=x2﹣2x﹣15,y=4x﹣23,交于A、B点(A在B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E再到达x轴上的某点F,最后运动到点B.若使点P动的总路径最短,则点P运动的总路径的长为( )
A.10 B.7 C.5 D.8
二.填空题
11抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为l,则b的值是 .
12.某商店将进货价为70元/个的商品按零售价100元/个出售时,每天能卖出20个,若零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价 元.
13.一名男生参加抛实心球测试,已知球的高度y(m)与水平距离x(m)之间的关系是,则这名男生抛实心球的成绩是 m.
14.学校准备建一个矩形花圃,其中一边靠墙,另外三边用周长为30米的篱笆围成,已知墙长为18米,设花圃垂直于墙的一边长为x米,花圃的面积为y平方米,写出y与x的函数关系式,并写出自变量x的取值范围 .
15.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为y=﹣x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.
16.某商品进货单价为30元,按40元一个销售能卖40个;若销售单价每涨1元,则销量减少1个.设涨价x元,利润为y元,则y与x的函数关系为 .
三.解答题
17.某商店销售一种进价50元/件的商品,经市场调查发现:该商品的每天销售量y(件)是售价x(元/件)的一次函数,其售价、销售量的二组对应值如下表:
售价x(元/件) 55 65
销售量y(件/天) 90 70
(1)若某天销售利润为800元,求该天的售价为多少元/件.
(2)由于某种原因,该商品进价提高了a元/件(a>0),商店售价不低于进价,物价部门规定该商品售价不得超过70元件,该商店在今后的销售中,每天能获得的销售最大利润是960元,求a的值.
18.喷洒酒精能有效杀灭“新型冠状肺炎”病毒.根据实验知道喷洒酒精在教室内空气中的浓度y(单位:mg/m3)与时间x(单位:h)的函数表达式为y=.其大致图象如图所示.请根据以上信息解答下列问题:
(1)试确定点A的坐标;
(2)根据经验,当教室空气中的药物浓度不低于1mg/m3时,杀灭“新型冠状肺炎”病毒的效果最佳,请通过计算说明单次喷洒酒精杀灭“新型冠状肺炎”病毒的效果处于最佳状态的时间为多少小时?
19.如图,在平面直角坐标系中,直线y=kx+1与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2﹣(6a﹣2)x+b与直线AC交于另一点B(4,3).
(1)求抛物线的表达式;
(2)已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求出m的值.
答案提示
1.D.2.D.3.D.4.D.5.C.6.C.7.D.8.C.9.C.10.A.
11.-3. 12.5. 13. 10. 14.y=﹣2x2+30x(6≤x<15).
15.8.
16.y=﹣x2+30x+400(0≤x≤40),
17.解:(1)依题意设y=kx+b,
则有,
解得:,
所以y=﹣2x+200,
若某天销售利润为800元,
则(x﹣50)(﹣2x+200)=800,
解得:x1=60,x2=90,
该天的售价为60元或者90元;
(2)设总利润为w,根据题意得,
w=(x﹣50﹣a)(﹣2x+200)
=﹣2x2+(300+2a)x﹣10000﹣200a
∵a>0,
∴对称轴x=>75,
∵﹣2<0,
∴抛物线的开口向下,
∵x≤70,
∴w随x的增大而增大,
当x=70时,w最大=960,
即960=﹣2×702+(300+2a)×70﹣10000﹣200a,
解得:a=4.
18.解:(1)由题意可得A为函数y=2x与y=﹣x2+6x﹣4的交点,
所以2x=﹣x2+6x﹣4,
解得x1=x2=2,代入y=2x得y=4,
可得A(2,4).
(2)当教室空气中的药物浓度不低于1mg/m3时,杀灭“新型冠状肺炎”病毒的效果最佳,
由(1)得m=2,
当0<x<2时,
令y=1,
2x=1,
x=;
当x≥2时,
令y=1,
﹣x2+6x﹣4=1
整理得x2﹣6x+5=0
解得x1=1(不合题意,舍去),x2=5,
所以x=5,
所以单次喷洒酒精杀灭“新型冠状肺炎”病毒的效果处于最佳状态的时间为(5﹣)=4.5小时.
19.解:(1)点C的坐标为(0,1),b=1,
将点B坐标代入代入一次函数表达式得:3=4k+1,解得:k=,
则一次函数表达式为:y=x+1,则点A坐标为(﹣2,0),
把点C.B坐标代入二次函数表达式得:3=a×42﹣4(6a﹣2)+1,解得:a=,
则二次函数表达式为:y=x2﹣x+1;
(2)①如下图,当∠AQB=90°时,
△ABQ与△AOC相似,m=4,
②当∠ABQ=90°时,△ABQ与△AOC相似,
AB==3,cos∠BAO==,
则AQ==,
则m=﹣2=,
即:m的值为4或.
