初中数学青岛版八年级下册 6.1平行四边形及其性质(第1课时) 课件(共25张)
文档属性
| 名称 | 初中数学青岛版八年级下册 6.1平行四边形及其性质(第1课时) 课件(共25张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 18:32:43 | ||
图片预览






文档简介
(共25张PPT)
第六章平行四边形
A
B
C
D
6.1.1 平行四边形及其性质
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
平行四边形的概念:
1、定义:两组对边分别平行的四边形叫平行四边形.
2、特征:a、属于四边形; b、有两组对边分别平行.
4、有关名称:
(3)对角,(4)邻角;
(5)高。
3、符号: 如平行四边形ABCD记作: ABCD; 读作:平行四边形ABCD
A
D
C
B
(1)对边,
(2)邻边;
∟
A
D
C
B
∟
E
F
G
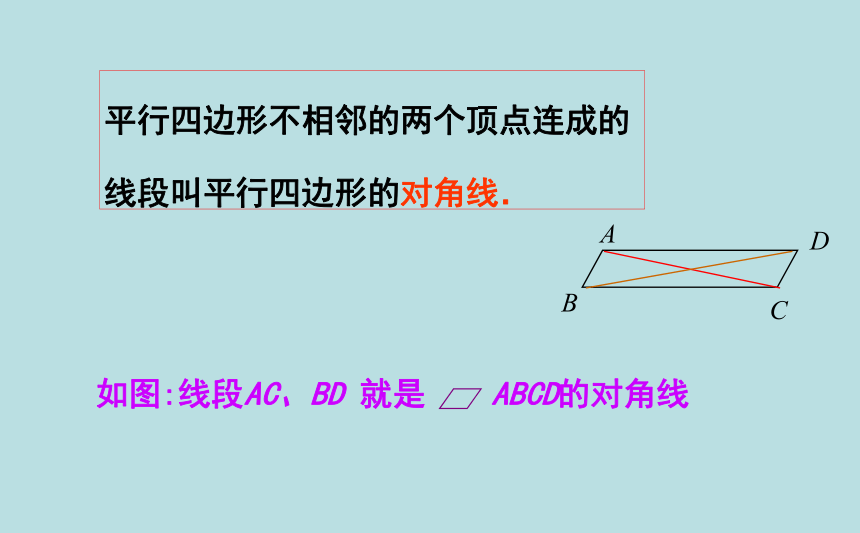
如图:线段AC、BD 就是 ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
典型例析
A
B
C
D
F
E
G
H
O
3
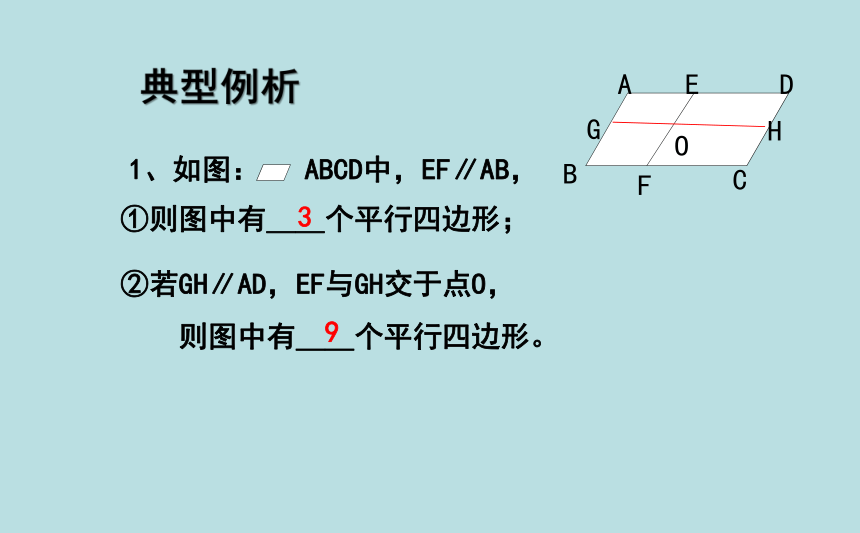
1、如图: ABCD中,EF∥AB,
①则图中有__个平行四边形;
②若GH∥AD,EF与GH交于点O,
则图中有__个平行四边形。
9
1.平行四边形的边具有哪些性质?说说你的理由。
2.平行四边形的角具有哪些性质?说说你的理由。
1.平行四边形的对边平行且相等
平行四边形的性质:
2.平行四边形的对角相等.
平行四边形的性质
定理1:平行四边形的对边相等.
B
D
C
A
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
分析:要证明AB=CD,BC=DA可转化全等三角形的对应边来证明,于是可作辅助线来达到目的.
证明:连接AC.
∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥DA.
∴∠1=∠2, ∠3=∠4.
在△ABC和△CDA中
∠1=∠2, AC=CA, ∠3=∠4
∴△ABC≌△CDA(ASA).
∴AB=CD,BC=DA.
1
2
3
4
由上述证明过程你能得到平行四边形的对角相等吗?
平行四边形的对边平行.
∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
性质定理1:平行四边形的对边相等.
总结
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
典型例析
例:如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______
ABCD中,
A:基础知识:
B:变式训练:
1、若∠A+ ∠C= 200°,则∠A=______ 、∠B=______
2、若∠A:∠B= 5:4,则∠C=______ 、∠D=______
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
例:如图在
ABCD中
A基础知识:
1、若AB=1㎝,BC=2 ㎝
则
ABCD的周长=______
2、若AB=4㎝, BC=______
ABCD的周长为18 ㎝,
B变式训练:
1、若AB:BC=3:4,周长为14㎝,则CD= ,DA=
2、若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____
C拓展延伸:
若AB=x-4,BC=x+3,CD=6㎝,则AD=______
C
D
A
B
6cm
5cm
3cm
4cm
8cm
28cm
13cm
典型例析
——
——
夹在两条平行线间的平行线段相等.
已知:如图,直线MN∥PQ,线段AB∥CD,且AB,CD与MN,PQ分别相交于点A,D,B,C.
求证:AB=CD.
分析:可利用平行四边形边的对边相等来证明.
证明:
∵MN∥PQ,AB∥CD.
∴四边形ABCD是平行四边形.
∴AB=CD.
B
D
C
A
M
N
P
Q
已知直线a //b,过直线a上任意两点,A,B分别向直线b作垂线,交直线b于点C、点D。
(如右图)则AC=BD
A
C
D
B
a
b
a//b
AC//BD
四边形ACDB是平行四边形
AC=BD
两条平行线中,其中一条直线上任意一点到另一条直线的距离相等。
两条平行线中,其中一条
直线上任意一点到另一条直线
的距离,叫做这两条平行线之间的距离。
如:AC、BD均是平行线a与b之间的距离。
A
C
D
B
a
b
F
E
平行线之间的距离:
选择题:
(1)下列命题中,正确的个数是( )。
①一组对边平行的四边形叫做平行四边形
②平行四边形的对角相等,邻角互补;
③夹在两平行线之间的线段相等
④两条平行线之间的距离相等
A、1个 B、2个 C、3个 D、4个
B
试一试
如图,平行四边形ABCD中,点E,F在对角线BD上,且AE|| CF.
求证:AE=CF.
A
B
C
D
E
F
平行四边形的对边平行且相等;
B
D
C
A
平行四边形的对角相等;邻角互补。
有两组对边分别平行的四边形是平行四边形。
C:拓展延伸:
例:如图,在
ABCD中,
1、∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2 C、2:3:3:2 D、2:2:3:3
C
D
A
B
2、连接AC,若∠D=80°,∠DAC=40°则,∠B=___ ,
∠BAC=____,
3、若AE,AF为高,且∠EAF=60°
则∠C= _____,∠B=_____.
C
D
A
B
E
F
B
80°
60°
120°
60°
BE平分∠ABC,
4
ABCD中, AB=5,BC=9,
5、如图,
则DE= _________
A
D
C
B
E
1
2
3
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知)
∴ ∠A=∠C=52°(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D= 180 °-∠A= 180 - 52°=128 °
在 ABCD中,已知∠A=52 °,求其余三个角的度数。
A
B
C
D
52°
典型例析
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
变式练习
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180 - 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
解:∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
又∵□ABCD的周长为60cm.
∴AB + BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则 1.5BC + BC=30 , 解得 BC=12 (cm).
而 AB=1.5×12=18 (cm).
已知:平行四边形 ABCD的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
变式练习
2、在 ABCD 中,∠ADC=120°, ∠CAD=20°,则
∠ABC= , ∠CAB= .
1.已知,在 ABCD中,∠1=60°,则:∠A= ,
∠B= ,∠C= ,∠D= .
(1小题)
(2小题)
60 °
120 °
60 °
120 °
120 °
40 °
1
随堂练习
D
A
B
C
A
B
C
D
第六章平行四边形
A
B
C
D
6.1.1 平行四边形及其性质
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
平行四边形的概念:
1、定义:两组对边分别平行的四边形叫平行四边形.
2、特征:a、属于四边形; b、有两组对边分别平行.
4、有关名称:
(3)对角,(4)邻角;
(5)高。
3、符号: 如平行四边形ABCD记作: ABCD; 读作:平行四边形ABCD
A
D
C
B
(1)对边,
(2)邻边;
∟
A
D
C
B
∟
E
F
G
如图:线段AC、BD 就是 ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
典型例析
A
B
C
D
F
E
G
H
O
3
1、如图: ABCD中,EF∥AB,
①则图中有__个平行四边形;
②若GH∥AD,EF与GH交于点O,
则图中有__个平行四边形。
9
1.平行四边形的边具有哪些性质?说说你的理由。
2.平行四边形的角具有哪些性质?说说你的理由。
1.平行四边形的对边平行且相等
平行四边形的性质:
2.平行四边形的对角相等.
平行四边形的性质
定理1:平行四边形的对边相等.
B
D
C
A
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
分析:要证明AB=CD,BC=DA可转化全等三角形的对应边来证明,于是可作辅助线来达到目的.
证明:连接AC.
∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥DA.
∴∠1=∠2, ∠3=∠4.
在△ABC和△CDA中
∠1=∠2, AC=CA, ∠3=∠4
∴△ABC≌△CDA(ASA).
∴AB=CD,BC=DA.
1
2
3
4
由上述证明过程你能得到平行四边形的对角相等吗?
平行四边形的对边平行.
∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
性质定理1:平行四边形的对边相等.
总结
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
典型例析
例:如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______
ABCD中,
A:基础知识:
B:变式训练:
1、若∠A+ ∠C= 200°,则∠A=______ 、∠B=______
2、若∠A:∠B= 5:4,则∠C=______ 、∠D=______
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
例:如图在
ABCD中
A基础知识:
1、若AB=1㎝,BC=2 ㎝
则
ABCD的周长=______
2、若AB=4㎝, BC=______
ABCD的周长为18 ㎝,
B变式训练:
1、若AB:BC=3:4,周长为14㎝,则CD= ,DA=
2、若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____
C拓展延伸:
若AB=x-4,BC=x+3,CD=6㎝,则AD=______
C
D
A
B
6cm
5cm
3cm
4cm
8cm
28cm
13cm
典型例析
——
——
夹在两条平行线间的平行线段相等.
已知:如图,直线MN∥PQ,线段AB∥CD,且AB,CD与MN,PQ分别相交于点A,D,B,C.
求证:AB=CD.
分析:可利用平行四边形边的对边相等来证明.
证明:
∵MN∥PQ,AB∥CD.
∴四边形ABCD是平行四边形.
∴AB=CD.
B
D
C
A
M
N
P
Q
已知直线a //b,过直线a上任意两点,A,B分别向直线b作垂线,交直线b于点C、点D。
(如右图)则AC=BD
A
C
D
B
a
b
a//b
AC//BD
四边形ACDB是平行四边形
AC=BD
两条平行线中,其中一条直线上任意一点到另一条直线的距离相等。
两条平行线中,其中一条
直线上任意一点到另一条直线
的距离,叫做这两条平行线之间的距离。
如:AC、BD均是平行线a与b之间的距离。
A
C
D
B
a
b
F
E
平行线之间的距离:
选择题:
(1)下列命题中,正确的个数是( )。
①一组对边平行的四边形叫做平行四边形
②平行四边形的对角相等,邻角互补;
③夹在两平行线之间的线段相等
④两条平行线之间的距离相等
A、1个 B、2个 C、3个 D、4个
B
试一试
如图,平行四边形ABCD中,点E,F在对角线BD上,且AE|| CF.
求证:AE=CF.
A
B
C
D
E
F
平行四边形的对边平行且相等;
B
D
C
A
平行四边形的对角相等;邻角互补。
有两组对边分别平行的四边形是平行四边形。
C:拓展延伸:
例:如图,在
ABCD中,
1、∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2 C、2:3:3:2 D、2:2:3:3
C
D
A
B
2、连接AC,若∠D=80°,∠DAC=40°则,∠B=___ ,
∠BAC=____,
3、若AE,AF为高,且∠EAF=60°
则∠C= _____,∠B=_____.
C
D
A
B
E
F
B
80°
60°
120°
60°
BE平分∠ABC,
4
ABCD中, AB=5,BC=9,
5、如图,
则DE= _________
A
D
C
B
E
1
2
3
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知)
∴ ∠A=∠C=52°(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D= 180 °-∠A= 180 - 52°=128 °
在 ABCD中,已知∠A=52 °,求其余三个角的度数。
A
B
C
D
52°
典型例析
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
变式练习
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180 - 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
解:∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
又∵□ABCD的周长为60cm.
∴AB + BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则 1.5BC + BC=30 , 解得 BC=12 (cm).
而 AB=1.5×12=18 (cm).
已知:平行四边形 ABCD的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
变式练习
2、在 ABCD 中,∠ADC=120°, ∠CAD=20°,则
∠ABC= , ∠CAB= .
1.已知,在 ABCD中,∠1=60°,则:∠A= ,
∠B= ,∠C= ,∠D= .
(1小题)
(2小题)
60 °
120 °
60 °
120 °
120 °
40 °
1
随堂练习
D
A
B
C
A
B
C
D
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
