2021-2022学年人教版八年级数学下册 18.2.3正方形 练习卷(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册 18.2.3正方形 练习卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 271.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览




文档简介
18.2.3正方形
一、单选题
1.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
2.如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF=( )度
A.30° B.45° C.50° D.60°
3.如图,正方形ABCD的对角线AC、BD交于点O,AO=3,则AB的长为( )
A.2 B.3 C. D.
4.如图,长方形ABCD的周长是12cm,分别以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为20 ,那么长方形ABCD的面积是( )
A.6 B.7 C.8 D.4
5.下列命题中,正确的是( ).
A.有一个角是的四边形是矩形
B.对角线互相平分且相等的四边形是菱形
C.两组邻角相等的四边形是平行四边形
D.对角线互相垂直且相等的平行四边形是正方形
6.已知在平行四边形ABCD中,∠A=90°,如果添加一个条件,可使该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C.AD=BC D.BC=CD
7.过正方形的中心作两条互相垂直的直线,则以这两条直线与正方形各边交点为顶点的四边形是( )
A.筝形 B.矩形 C.菱形 D.正方形
8.如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( )
A.2 B. C. D.
9.如图,在边长为的正方形ABCD中,点E是对角线AC上一点,且于点F,连接DE,当时,( )
A.1 B. C. D.
10.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=S△ABE+S△ADF,其中正确的结论有( )个.
A.5 B.4 C.3 D.2
二、填空题
11.如图在3×3的正方形网格中∠1+∠2﹣∠3+∠4+∠5=___度.
12.如图,在正方形中.若以为底边向其形外作等腰直角,连接,则的长为______.
13.如图,两个边长均为2的正方形重叠在一起,O是正方形ABCD的中心,则阴影部分的面积是_____.
14.如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为_____.
15.正方形的边长为4,点在对角线上(可与点重合),,点在正方形的边上.下面四个结论中,
①存在无数个四边形是平行四边形;
②存在无数个四边形是菱形;
③存在无数个四边形是矩形;
④至少存在一个四边形是正方形.
所有正确结论的序号是_______.
三、解答题
16.如图,正方形中,点E、F分别是边上的点,且.求的度数.
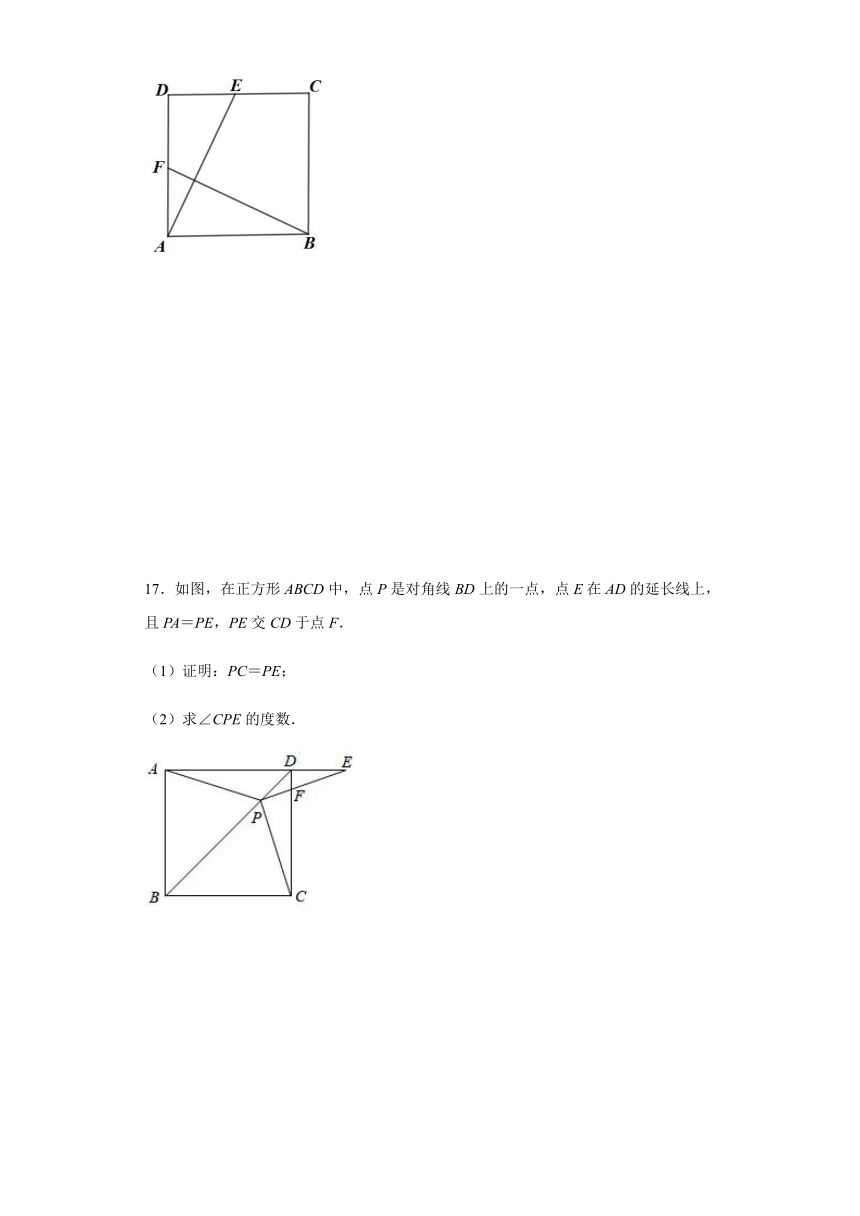
17.如图,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)证明:PC=PE;
(2)求∠CPE的度数.
18.已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF.联结EF、FG、CH、HE.
(1)求证:四边形EFGH是矩形.
(2)若∠B=45度,求证:四边形EFGH是正方形.
19.如图,在中,,是中线,是的中点,过点作AFBC交BE的延长线于F,连接CF.
(1)求证:;
(2)如果.试判断四边形的形状,并证明你的结论.
20.在正方形ABCD中,点E是CD边上任意一点.连接AE,过点B作BF⊥AE于F.交AD于H.
(1)如图1,过点D作DG⊥AE于G,求证:△AFB≌△DGA;
(2)如图2,点E为CD的中点,连接DF,求证:FH+FE=DF;
(3)如图3,AB=1,连接EH,点P为EH的中点,在点E从点D运动到点C的过程中,点P随之运动,请直接写出点P运动的路径长.
试卷第1页,共3页
答案
1.A
2.B
3.D
4.C
5.D
6.D
7.D
8.D
9.C
10.B
11.135°
12.
13.1
14.45°##45度
15.①②④
16.解:∵在正方形中,
∴AD=AB,∠D=∠FAB=90°,
在和中,
,
∴(HL),
∴,
又∵,
∴.
故答案为:.
17.(1)证明:∵四边形ABCD是正方形,BD是正方形ABCD的对角线,
∴AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE,
(2)解:由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD,
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPE=∠EDF=90°.
18.(1)证明∵四边形ABCD是菱形
∴ADBC,AB=BC=CD=AD,∠BAD=∠BCD,∠ABC=∠ADC
∴∠ABC+∠BAD=180°
∵AF⊥BC ,CH⊥AD
∴∠AFC=∠AHC=90°
∵ADBC
∴ ∠FAH=180°-∠AFC=90°
∴四边形AFCH为矩形,
∴AH=CF
∵AE=AH,CG=CF
∴AH=CF=AE=CG,BF=BE=DH=DG
∴△AEH≌△CFG(SAS),△BEF≌△DGH(SAS)
∴EH=FG,EF=GH
∴四边形EFGH是平行四边形
∵BE=BF
∴△BEF是等腰三角形
∴∠BEF=∠BFE=(180°-∠ABC)=90°-∠ABC
同理可得∠AEH=∠BAD
∴∠BFE+∠AEH=(∠ABC+∠BAD)=90°
∴∠HEF=180°-(∠BFE+∠AEH)=90°
∴四边形EFGH是矩形.
(2)证明:如图,连结BD,FH,AC,设BD、AC、FH相交于点O.
∵四边形ABCD是菱形
∴ADBC,AB=BC=CD=AD, AC⊥BD
∴∠ADB=∠CBD,△ABD是等腰三角形,∠BOC==90°
∴∠ABD=∠ADB
∴∠ABD=∠CBD=∠ABC=22.5°
∴∠BCO=180°-∠CBD-∠BOC=67.5°
∵四边形AFCH为矩形
∴OF=OC,∠AFC=90°
∴△FOC是等腰三角形
∴∠OFC=∠BCO=67.5°
∴∠AFH=∠AFC-∠OFC=22.5°
∵BE=BF
∴△BEF是等腰三角形
∴∠BEF=∠BFE=(180°-∠ABC)=90°-∠ABC=67.5°
∵AF⊥BC
∴∠AFB=90°
∴∠AFE=∠AFB-∠BFE=22.5°
∴∠EFH=∠AFE+∠AFH=45°
∵四边形EFGH是矩形
∴∠FEH=90°
∴∠EHF=180-∠FEH-∠EFH=45°
∴∠EFH=∠EHF
∴EF=EH
∴四边形EFGH是正方形.
19.(1)证明:∵AD 是中线, E 是 AD 的中点,
∴AF∥BC,
,
,
在和中,
,
),
,
在中,,是中线,
,
;
(2)解:四边形是正方形,理由如下;
,,
四边形是平行四边形,
,是中线,
,
,
四边形是正方形.
20.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°
∵DG⊥AE,BF⊥AE
∴∠AFB=∠DGA=90°
∵∠FAB+∠DAG=90°,∠DAG+∠ADG=90°
∴∠BAF=∠ADG
在△AFB和△DGA中
∵
∴△AFB≌△DGA(AAS).
(2)证明:如图2,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J
由题意知∠BAH=∠ADE=90°,AB=AD=CD
∵BF⊥AE
∴∠AFB=90°
∵∠DAE+∠EAB=90°,∠EAB+∠ABH=90°
∴∠DAE=∠ABH
在△ABH和△DAE中
∵
∴△ABH≌△DAE(ASA)
∴AH=DE
∵点E为CD的中点
∴DE=EC= CD
∴AH=DH
∴DE=DH
∵DJ⊥BJ,DK⊥AE
∴∠J=∠DKE=∠KFJ=90°
∴四边形DKFJ是矩形
∴∠JDK=∠ADC=90°
∴∠JDH=∠KDE
在△DJH和△DKE中
∵
∴△DJH≌△DKE(AAS)
∴DJ=DK,JH=EK
∴四边形DKFJ是正方形
∴FK=FJ=DK=DJ
∴DF=FJ
∴
∴FH+FE=FJ﹣HJ+FK+KE=2FJ=DF.
(3)
解:如图3,取AD的中点Q,连接PQ,延长QP交CD于R,过点P作PT⊥CD于T,PK⊥AD于K,设PT=b
由(2)得△ABH≌△DAE(ASA)
∴AH=DE
∵∠EDH=90°,点P为EH的中点
∴PD=EH=PH=PE
∵PK⊥DH,PT⊥DE
∴∠PKD=∠KDT=∠PTD=90°
∴四边形PTDK是矩形
∴PT=DK=b,PK=DT
∵PH=PD=PE,PK⊥DH,PT⊥DE
∴PT是△DEH的中位线
∴DH=2DK=2b,DE=2DT
∴AH=DE=1﹣2b
∴PK= DE=﹣b,QK=DQ﹣DK=﹣b
∴PK=QK
∵∠PKQ=90°
∴△PKQ是等腰直角三角形
∴∠KQP=45°
∴点P在线段QR上运动,△DQR是等腰直角三角形
∴QR=DQ=
∴点P的运动轨迹的长为.答案第1页,共2页
答案第1页,共2页
一、单选题
1.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
2.如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF=( )度
A.30° B.45° C.50° D.60°
3.如图,正方形ABCD的对角线AC、BD交于点O,AO=3,则AB的长为( )
A.2 B.3 C. D.
4.如图,长方形ABCD的周长是12cm,分别以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为20 ,那么长方形ABCD的面积是( )
A.6 B.7 C.8 D.4
5.下列命题中,正确的是( ).
A.有一个角是的四边形是矩形
B.对角线互相平分且相等的四边形是菱形
C.两组邻角相等的四边形是平行四边形
D.对角线互相垂直且相等的平行四边形是正方形
6.已知在平行四边形ABCD中,∠A=90°,如果添加一个条件,可使该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C.AD=BC D.BC=CD
7.过正方形的中心作两条互相垂直的直线,则以这两条直线与正方形各边交点为顶点的四边形是( )
A.筝形 B.矩形 C.菱形 D.正方形
8.如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( )
A.2 B. C. D.
9.如图,在边长为的正方形ABCD中,点E是对角线AC上一点,且于点F,连接DE,当时,( )
A.1 B. C. D.
10.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=S△ABE+S△ADF,其中正确的结论有( )个.
A.5 B.4 C.3 D.2
二、填空题
11.如图在3×3的正方形网格中∠1+∠2﹣∠3+∠4+∠5=___度.
12.如图,在正方形中.若以为底边向其形外作等腰直角,连接,则的长为______.
13.如图,两个边长均为2的正方形重叠在一起,O是正方形ABCD的中心,则阴影部分的面积是_____.
14.如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为_____.
15.正方形的边长为4,点在对角线上(可与点重合),,点在正方形的边上.下面四个结论中,
①存在无数个四边形是平行四边形;
②存在无数个四边形是菱形;
③存在无数个四边形是矩形;
④至少存在一个四边形是正方形.
所有正确结论的序号是_______.
三、解答题
16.如图,正方形中,点E、F分别是边上的点,且.求的度数.
17.如图,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)证明:PC=PE;
(2)求∠CPE的度数.
18.已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF.联结EF、FG、CH、HE.
(1)求证:四边形EFGH是矩形.
(2)若∠B=45度,求证:四边形EFGH是正方形.
19.如图,在中,,是中线,是的中点,过点作AFBC交BE的延长线于F,连接CF.
(1)求证:;
(2)如果.试判断四边形的形状,并证明你的结论.
20.在正方形ABCD中,点E是CD边上任意一点.连接AE,过点B作BF⊥AE于F.交AD于H.
(1)如图1,过点D作DG⊥AE于G,求证:△AFB≌△DGA;
(2)如图2,点E为CD的中点,连接DF,求证:FH+FE=DF;
(3)如图3,AB=1,连接EH,点P为EH的中点,在点E从点D运动到点C的过程中,点P随之运动,请直接写出点P运动的路径长.
试卷第1页,共3页
答案
1.A
2.B
3.D
4.C
5.D
6.D
7.D
8.D
9.C
10.B
11.135°
12.
13.1
14.45°##45度
15.①②④
16.解:∵在正方形中,
∴AD=AB,∠D=∠FAB=90°,
在和中,
,
∴(HL),
∴,
又∵,
∴.
故答案为:.
17.(1)证明:∵四边形ABCD是正方形,BD是正方形ABCD的对角线,
∴AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE,
(2)解:由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD,
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPE=∠EDF=90°.
18.(1)证明∵四边形ABCD是菱形
∴ADBC,AB=BC=CD=AD,∠BAD=∠BCD,∠ABC=∠ADC
∴∠ABC+∠BAD=180°
∵AF⊥BC ,CH⊥AD
∴∠AFC=∠AHC=90°
∵ADBC
∴ ∠FAH=180°-∠AFC=90°
∴四边形AFCH为矩形,
∴AH=CF
∵AE=AH,CG=CF
∴AH=CF=AE=CG,BF=BE=DH=DG
∴△AEH≌△CFG(SAS),△BEF≌△DGH(SAS)
∴EH=FG,EF=GH
∴四边形EFGH是平行四边形
∵BE=BF
∴△BEF是等腰三角形
∴∠BEF=∠BFE=(180°-∠ABC)=90°-∠ABC
同理可得∠AEH=∠BAD
∴∠BFE+∠AEH=(∠ABC+∠BAD)=90°
∴∠HEF=180°-(∠BFE+∠AEH)=90°
∴四边形EFGH是矩形.
(2)证明:如图,连结BD,FH,AC,设BD、AC、FH相交于点O.
∵四边形ABCD是菱形
∴ADBC,AB=BC=CD=AD, AC⊥BD
∴∠ADB=∠CBD,△ABD是等腰三角形,∠BOC==90°
∴∠ABD=∠ADB
∴∠ABD=∠CBD=∠ABC=22.5°
∴∠BCO=180°-∠CBD-∠BOC=67.5°
∵四边形AFCH为矩形
∴OF=OC,∠AFC=90°
∴△FOC是等腰三角形
∴∠OFC=∠BCO=67.5°
∴∠AFH=∠AFC-∠OFC=22.5°
∵BE=BF
∴△BEF是等腰三角形
∴∠BEF=∠BFE=(180°-∠ABC)=90°-∠ABC=67.5°
∵AF⊥BC
∴∠AFB=90°
∴∠AFE=∠AFB-∠BFE=22.5°
∴∠EFH=∠AFE+∠AFH=45°
∵四边形EFGH是矩形
∴∠FEH=90°
∴∠EHF=180-∠FEH-∠EFH=45°
∴∠EFH=∠EHF
∴EF=EH
∴四边形EFGH是正方形.
19.(1)证明:∵AD 是中线, E 是 AD 的中点,
∴AF∥BC,
,
,
在和中,
,
),
,
在中,,是中线,
,
;
(2)解:四边形是正方形,理由如下;
,,
四边形是平行四边形,
,是中线,
,
,
四边形是正方形.
20.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°
∵DG⊥AE,BF⊥AE
∴∠AFB=∠DGA=90°
∵∠FAB+∠DAG=90°,∠DAG+∠ADG=90°
∴∠BAF=∠ADG
在△AFB和△DGA中
∵
∴△AFB≌△DGA(AAS).
(2)证明:如图2,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J
由题意知∠BAH=∠ADE=90°,AB=AD=CD
∵BF⊥AE
∴∠AFB=90°
∵∠DAE+∠EAB=90°,∠EAB+∠ABH=90°
∴∠DAE=∠ABH
在△ABH和△DAE中
∵
∴△ABH≌△DAE(ASA)
∴AH=DE
∵点E为CD的中点
∴DE=EC= CD
∴AH=DH
∴DE=DH
∵DJ⊥BJ,DK⊥AE
∴∠J=∠DKE=∠KFJ=90°
∴四边形DKFJ是矩形
∴∠JDK=∠ADC=90°
∴∠JDH=∠KDE
在△DJH和△DKE中
∵
∴△DJH≌△DKE(AAS)
∴DJ=DK,JH=EK
∴四边形DKFJ是正方形
∴FK=FJ=DK=DJ
∴DF=FJ
∴
∴FH+FE=FJ﹣HJ+FK+KE=2FJ=DF.
(3)
解:如图3,取AD的中点Q,连接PQ,延长QP交CD于R,过点P作PT⊥CD于T,PK⊥AD于K,设PT=b
由(2)得△ABH≌△DAE(ASA)
∴AH=DE
∵∠EDH=90°,点P为EH的中点
∴PD=EH=PH=PE
∵PK⊥DH,PT⊥DE
∴∠PKD=∠KDT=∠PTD=90°
∴四边形PTDK是矩形
∴PT=DK=b,PK=DT
∵PH=PD=PE,PK⊥DH,PT⊥DE
∴PT是△DEH的中位线
∴DH=2DK=2b,DE=2DT
∴AH=DE=1﹣2b
∴PK= DE=﹣b,QK=DQ﹣DK=﹣b
∴PK=QK
∵∠PKQ=90°
∴△PKQ是等腰直角三角形
∴∠KQP=45°
∴点P在线段QR上运动,△DQR是等腰直角三角形
∴QR=DQ=
∴点P的运动轨迹的长为.答案第1页,共2页
答案第1页,共2页
