2021-2022学年北师大版九年级下册数学2.4二次函数的应用 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级下册数学2.4二次函数的应用 同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 152.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览



文档简介
2.4二次函数的应用 同步练习
一.选择题
1.服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )
A.150元 B.160元 C.170元 D.180元
2.把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A.y= -x2+50x B.y=x2-50x C.y= -x2+25x D.y= -2x2+25
3.如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是( )
﹣1≤x≤3 B.x≤﹣1 C.x≥1 D.x≤﹣1或x≥3
已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A B C D
5.一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s 0 1 2 3 4
滑行距离y1/s 0 4.5 14 28.5 48
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270 B.280 C.375 D.450
6.抛物线y=ax2+3ax+b的一部分图象如图,设该抛物线与x轴的交点为A(﹣5,0)和B,与y轴的交点为C,若△ACO∽△CBO,则∠CAB的正切值为( )
A. B. C. D.
7.如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB=1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为多少米( )
A.3.2 B.0.32 C.2.5 D.1.6
8.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售价为x元,则可卖出(350-10x)件商品,那么卖出商品所赚钱y元与售价x元之间的函数关系为( )
A.y=-10x2-560x+7 350
B.y=-10x2+560x-7 350
C.y=-10x2+350x
D.y=-10x2+350x-7 350
9.平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如图所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为( )
A.1.5 m B.1.625 m C.1.66 m D.1.67 m
10.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,△PCQ面积的最大值为( )
A.6 cm2 B.9 cm2 C.12 cm2 D.15 cm2
二.填空题
11把二次函数y=2x2-4x+5化成y=a(x-h)2+k的形式是 ,其图象开口方向 ,顶点坐标是 ,当x= 时,函数y有最 值,当x 时,y随x的增大而减小.
12.如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t(秒)之间的函数关系式为____
13.某商店销售一批头盔,售价为每顶60元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶40元,则该商店每月获得最大利润时,每顶头盔的售价为 元.
14.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,则水流的落地点C到水枪底部B的距离为 .
15.某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是 元.
三.解答题
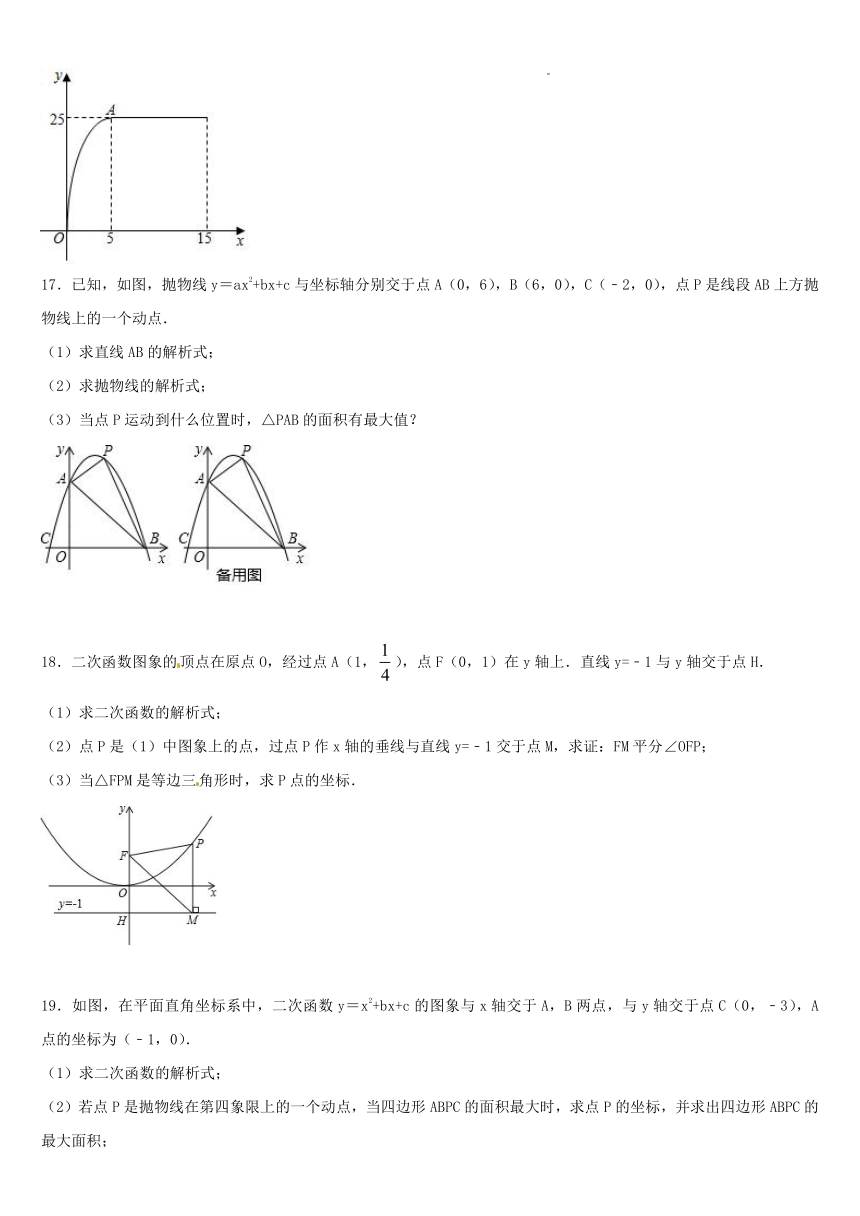
16.陆臻同学善于总结改进学习方法,他发现每解题1分钟学习收益量为2;对解题过程进行回顾反思效果会更好,用于回顾反思的时间x(单位:分钟)与学习收益量y的关系如图所示(其中OA是抛物线的一部分,A为抛物线的顶点).某一天他共有30分钟进行学习,且用于回顾反思的时间不能超过用于解题的时间.
(1)求陆臻回顾反思的学习收益量y与用于回顾反思的时间x之间的函数关系式;
(2)陆臻如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?(学习收益总量=解题的学习收益量+回顾反思的学习收益量)
17.已知,如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求直线AB的解析式;
(2)求抛物线的解析式;
(3)当点P运动到什么位置时,△PAB的面积有最大值?
18.二次函数图象的顶点在原点O,经过点A(1,),点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
19.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,﹣3),A点的坐标为(﹣1,0).
(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,当Q在什么位置时QA+QC最小,求出Q点的坐标,并求出此时△QAC的周长.
参考答案
1.A. 2.C.3.D.4.C 5.A.6.C.7.A..8.B.9.B.10.B.
11y=2(x-1)2+3 向上 (1,3) 1 小 <1
12.y=(20-2t)2.
13.55.
14.(2+2)m.
15.1800.
16.解:(1)当0≤x≤5时,设y=a(x﹣5)2+25,
把(0,0)代入,得:0=25a+25,
解得:a=﹣1,
∴y=﹣(x﹣5)2+25=﹣x2+10x;
当5<x≤15时,y=25.
综上,y=;
(2)设陆臻用于回顾反思的时间为x(0≤x≤15)分钟,学习效益总量为Z,则他用于解题的时间为(30﹣x)分钟.
当0≤x≤5时,
Z=﹣x2+10x+2(30﹣x)
=﹣x2+8x+60
=﹣(x﹣4)2+76.
∴当x=4时,Z最大=76.
当5<x≤15时,
Z=25+2(30﹣x)=﹣2x+85.
∵Z随x的增大而减小,
∴Z<﹣2×5+85=75.
综上所述,当x=4时,Z最大=76,此时30﹣x=26.
∴陆臻用于回顾反思的时间为4分钟,用于解题的时间为26分钟时,才能使这30分钟的学习收益总量最大.
17.解:(1)依题意设y=kx+b,
则有,
解得:,
所以y=﹣2x+200,
若某天销售利润为800元,
则(x﹣50)(﹣2x+200)=800,
解得:x1=60,x2=90,
该天的售价为60元或者90元;
(2)设总利润为w,根据题意得,
w=(x﹣50﹣a)(﹣2x+200)
=﹣2x2+(300+2a)x﹣10000﹣200a
∵a>0,
∴对称轴x=>75,
∵﹣2<0,
∴抛物线的开口向下,
∵x≤70,
∴w随x的增大而增大,
当x=70时,w最大=960,
即960=﹣2×702+(300+2a)×70﹣10000﹣200a,
解得:a=4.
18.解:(1)由题意可得A为函数y=2x与y=﹣x2+6x﹣4的交点,
所以2x=﹣x2+6x﹣4,
解得x1=x2=2,代入y=2x得y=4,
可得A(2,4).
(2)当教室空气中的药物浓度不低于1mg/m3时,杀灭“新型冠状肺炎”病毒的效果最佳,
由(1)得m=2,
当0<x<2时,
令y=1,
2x=1,
x=;
当x≥2时,
令y=1,
﹣x2+6x﹣4=1
整理得x2﹣6x+5=0
解得x1=1(不合题意,舍去),x2=5,
所以x=5,
所以单次喷洒酒精杀灭“新型冠状肺炎”病毒的效果处于最佳状态的时间为(5﹣)=4.5小时.
19.解:(1)点C的坐标为(0,1),b=1,
将点B坐标代入代入一次函数表达式得:3=4k+1,解得:k=,
则一次函数表达式为:y=x+1,则点A坐标为(﹣2,0),
把点C.B坐标代入二次函数表达式得:3=a×42﹣4(6a﹣2)+1,解得:a=,
则二次函数表达式为:y=x2﹣x+1;
(2)①如下图,当∠AQB=90°时,
△ABQ与△AOC相似,m=4,
②当∠ABQ=90°时,△ABQ与△AOC相似,
AB==3,cos∠BAO==,
则AQ==,
则m=﹣2=,
即:m的值为4或.
一.选择题
1.服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )
A.150元 B.160元 C.170元 D.180元
2.把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A.y= -x2+50x B.y=x2-50x C.y= -x2+25x D.y= -2x2+25
3.如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是( )
﹣1≤x≤3 B.x≤﹣1 C.x≥1 D.x≤﹣1或x≥3
已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A B C D
5.一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s 0 1 2 3 4
滑行距离y1/s 0 4.5 14 28.5 48
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270 B.280 C.375 D.450
6.抛物线y=ax2+3ax+b的一部分图象如图,设该抛物线与x轴的交点为A(﹣5,0)和B,与y轴的交点为C,若△ACO∽△CBO,则∠CAB的正切值为( )
A. B. C. D.
7.如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB=1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为多少米( )
A.3.2 B.0.32 C.2.5 D.1.6
8.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售价为x元,则可卖出(350-10x)件商品,那么卖出商品所赚钱y元与售价x元之间的函数关系为( )
A.y=-10x2-560x+7 350
B.y=-10x2+560x-7 350
C.y=-10x2+350x
D.y=-10x2+350x-7 350
9.平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如图所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为( )
A.1.5 m B.1.625 m C.1.66 m D.1.67 m
10.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,△PCQ面积的最大值为( )
A.6 cm2 B.9 cm2 C.12 cm2 D.15 cm2
二.填空题
11把二次函数y=2x2-4x+5化成y=a(x-h)2+k的形式是 ,其图象开口方向 ,顶点坐标是 ,当x= 时,函数y有最 值,当x 时,y随x的增大而减小.
12.如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t(秒)之间的函数关系式为____
13.某商店销售一批头盔,售价为每顶60元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶40元,则该商店每月获得最大利润时,每顶头盔的售价为 元.
14.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,则水流的落地点C到水枪底部B的距离为 .
15.某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是 元.
三.解答题
16.陆臻同学善于总结改进学习方法,他发现每解题1分钟学习收益量为2;对解题过程进行回顾反思效果会更好,用于回顾反思的时间x(单位:分钟)与学习收益量y的关系如图所示(其中OA是抛物线的一部分,A为抛物线的顶点).某一天他共有30分钟进行学习,且用于回顾反思的时间不能超过用于解题的时间.
(1)求陆臻回顾反思的学习收益量y与用于回顾反思的时间x之间的函数关系式;
(2)陆臻如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?(学习收益总量=解题的学习收益量+回顾反思的学习收益量)
17.已知,如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求直线AB的解析式;
(2)求抛物线的解析式;
(3)当点P运动到什么位置时,△PAB的面积有最大值?
18.二次函数图象的顶点在原点O,经过点A(1,),点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
19.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,﹣3),A点的坐标为(﹣1,0).
(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,当Q在什么位置时QA+QC最小,求出Q点的坐标,并求出此时△QAC的周长.
参考答案
1.A. 2.C.3.D.4.C 5.A.6.C.7.A..8.B.9.B.10.B.
11y=2(x-1)2+3 向上 (1,3) 1 小 <1
12.y=(20-2t)2.
13.55.
14.(2+2)m.
15.1800.
16.解:(1)当0≤x≤5时,设y=a(x﹣5)2+25,
把(0,0)代入,得:0=25a+25,
解得:a=﹣1,
∴y=﹣(x﹣5)2+25=﹣x2+10x;
当5<x≤15时,y=25.
综上,y=;
(2)设陆臻用于回顾反思的时间为x(0≤x≤15)分钟,学习效益总量为Z,则他用于解题的时间为(30﹣x)分钟.
当0≤x≤5时,
Z=﹣x2+10x+2(30﹣x)
=﹣x2+8x+60
=﹣(x﹣4)2+76.
∴当x=4时,Z最大=76.
当5<x≤15时,
Z=25+2(30﹣x)=﹣2x+85.
∵Z随x的增大而减小,
∴Z<﹣2×5+85=75.
综上所述,当x=4时,Z最大=76,此时30﹣x=26.
∴陆臻用于回顾反思的时间为4分钟,用于解题的时间为26分钟时,才能使这30分钟的学习收益总量最大.
17.解:(1)依题意设y=kx+b,
则有,
解得:,
所以y=﹣2x+200,
若某天销售利润为800元,
则(x﹣50)(﹣2x+200)=800,
解得:x1=60,x2=90,
该天的售价为60元或者90元;
(2)设总利润为w,根据题意得,
w=(x﹣50﹣a)(﹣2x+200)
=﹣2x2+(300+2a)x﹣10000﹣200a
∵a>0,
∴对称轴x=>75,
∵﹣2<0,
∴抛物线的开口向下,
∵x≤70,
∴w随x的增大而增大,
当x=70时,w最大=960,
即960=﹣2×702+(300+2a)×70﹣10000﹣200a,
解得:a=4.
18.解:(1)由题意可得A为函数y=2x与y=﹣x2+6x﹣4的交点,
所以2x=﹣x2+6x﹣4,
解得x1=x2=2,代入y=2x得y=4,
可得A(2,4).
(2)当教室空气中的药物浓度不低于1mg/m3时,杀灭“新型冠状肺炎”病毒的效果最佳,
由(1)得m=2,
当0<x<2时,
令y=1,
2x=1,
x=;
当x≥2时,
令y=1,
﹣x2+6x﹣4=1
整理得x2﹣6x+5=0
解得x1=1(不合题意,舍去),x2=5,
所以x=5,
所以单次喷洒酒精杀灭“新型冠状肺炎”病毒的效果处于最佳状态的时间为(5﹣)=4.5小时.
19.解:(1)点C的坐标为(0,1),b=1,
将点B坐标代入代入一次函数表达式得:3=4k+1,解得:k=,
则一次函数表达式为:y=x+1,则点A坐标为(﹣2,0),
把点C.B坐标代入二次函数表达式得:3=a×42﹣4(6a﹣2)+1,解得:a=,
则二次函数表达式为:y=x2﹣x+1;
(2)①如下图,当∠AQB=90°时,
△ABQ与△AOC相似,m=4,
②当∠ABQ=90°时,△ABQ与△AOC相似,
AB==3,cos∠BAO==,
则AQ==,
则m=﹣2=,
即:m的值为4或.
