2021-2022学年人教版数学八年级下册第18章平行四边形 单元巩固练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册第18章平行四边形 单元巩固练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 280.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 20:23:22 | ||
图片预览


文档简介
2021~2022学年度第二学期八年级数学单元巩固练习(三)
(第十八章《平行四边形》)
题 号 一 二 三 总 分
得 分
一、选择题(本大题共6个小题,每小题3分,共18分)
1.下列性质中,平行四边形不一定具备是( )
A.邻角互补 B.对角互补 C.对边相等 D.对角线互相平分
2.将一矩形纸条按如图所示折叠,则∠1的度数为( )
A.72° B.84° C.63° D.76°
3.已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
4.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )
A.3 B.4 C.5 D.6
如图,四边形是菱形,对角线,相交于点,,,点是上一动点,点是的中点,则的最小值为( )
A. B. C.3 D.
6.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
(
第6题
) (
第4题
)A.8 B.8 C.4 D.6
(
第2题
)
(
第5题
)
二、填空题(本大题共6个小题,每小题3分,满分18分)
7.过矩形ABCD的四个顶点作对角线AC,BD的平行线,分别相交于E,F,G,H四点,则四边形EFGH为 .
8.如图,在△ABC中,AB=6,BC=8,AC=4,D、E、F分别为BC、AC、AB中点,连接DE、FE,则四边形BDEF的周长是 .
9.如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知BC=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为 cm.
如图,在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的度数是 .
(
第
11
题
) (
第
10
题
) (
第
9
题
) (
第8题
)
11.如图,在矩形纸片ABCD中,AB=4,BC=8,将纸片折叠,使点C与点A重合,则折痕EF的长是 .
12.已知点A(2,2),B(﹣2,0),C(3,﹣1),且以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为: .
三、解答题(共64分)
13.(4分)如图所示,在平行四边形ABCD中,点E,F分别在边BC和AD上,且CE=AF,求证:△ABE ≌ △CDF.
14.(4分)如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,分别在图1、图2中按要求作图(保留作图痕迹,不这写作法).
(1)在图1中,在AB边上求作一点N,连接CN,使得CN=AM;
(2)在图2中,在AD边上求作一点Q,连接CQ,使得CQ=AM.
15.(6分)如图,在菱形ABCD中,∠A与∠B的度数比为1:2,周长是48.
(1)求两条对角线的长度.
(2)求菱形ABCD的面积.
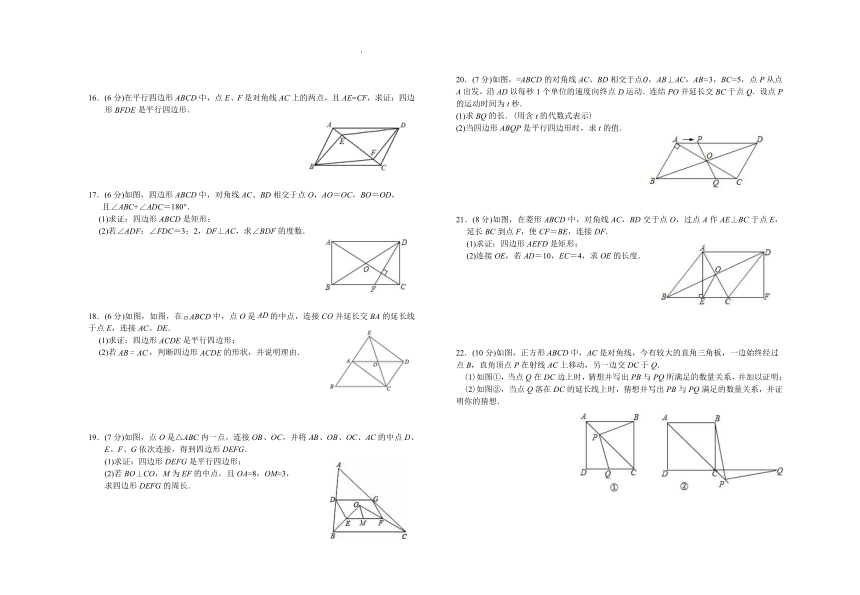
(6分)在平行四边形ABCD中,点E、F是对角线AC上的两点,且AE=CF,求证:四边形BFDE是平行四边形.
(6分)如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,
且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
18.(6分)如图,如图,在中,点O是的中点,连接CO并延长交BA的延长线于点E,连接AC、DE.
(1)求证:四边形是平行四边形;
(2)若,判断四边形的形状,并说明理由.
19.(7分)如图,点O是△ABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若BO⊥CO,M为EF的中点,且OA=8,OM=3,
求四边形DEFG的周长.
20.(7分)如图, ABCD的对角线AC、BD相交于点,AB⊥AC,AB=3,BC=5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连结PO并延长交BC于点Q.设点P的运动时间为t秒.
(1)求BQ的长.(用含t的代数式表示)
(2)当四边形ABQP是平行四边形时,求t的值.
21.(8分)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AD=10,EC=4,求OE的长度.
22.(10分)如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
(三)
B 2.A 3.B 4.B 5.A 6.D
7.菱形 8.14 9.5 10.119° 11.
12.(﹣1,﹣3)或(﹣3,3)或(5,1)
13.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
∵CE=AF,∴AD-AF=BC-CE,即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS)
14.解:(1)如图1,CN即为所求.
(2)如图2,CQ即为所求.
15.(1)解:(1)∵菱形ABCD的周长是48cm,
∴AB=BC=CD=DA=12cm,
又∵∠ABC与∠BAD的度数比为1:2,∠ABC=60°,
∴△ABC是正三角形,AC=AB=12cm,又∠ABO=30°,
∴AO=6cm,BO=cm,BD=cm,
(2)∴S菱形ABCD=AC BD=cm2.
16.证明:如图,连接 交于
,
四边形是平行四边形.
17.解:(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.
18.(1)证明:在ABCD中,AB∥CD,∴,
∵点O为AD的中点,∴,
在与中,
∵,,,
∴,∴,
又∵BE∥CD ,∴四边形ACDE是平行四边形;
(2)解:由(1)知四边形ACDE是平行四边形,,
∵,∴,
∴四边形ACDE是菱形.
19.(1)证明:∵D、G分别是AB、AC的中点,
∴DG∥BC,DG=BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF=BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形;
(2)解:连接AO,
∵BO⊥CO,M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,∴DG=EF=6,
∵D是AB的中点,E是BO的中点,∴DE=AO=4,
∴四边形DEFG的周长为:4+4+6+6=20.
20.解:(1)四边形是平行四边形,
,,,
,≌,
,
,;
,
当时,四边形是平行四边形,
即,,
当为秒时,四边形是平行四边形.
21.(1)证明:∵四边形ABCD是菱形,∴AD∥BC且AD=BC,
∵BE=CF,∴BC=EF,∴AD=EF,
∵AD∥EF,∴四边形AEFD是平行四边形,
∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,AD=10,
∴AD=AB=BC=10,
∵EC=4,∴BE=10﹣4=6,
在Rt△ABE中,AE=,
在Rt△AEC中,AC=,
∵四边形ABCD是菱形,∴OA=OC,∴OE=AC=.
22.证明:过P作PE⊥BC于E,PF⊥CD于F,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,∴PF=PE,
∴四边形PECF为正方形,
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,∴∠BPE=∠QPF,
又∵∠PEQ=∠PEB=90°,∴Rt△PQF≌Rt△PBE(ASA),
∴PB=PQ;
(2)PB=PQ,
证明:过P作PE⊥BC延长线于E,PF⊥QD于F,
∵P,C为正方形对角线AC上的点,
∴PC平分∠ECF,∠DCB=90°,
∴PF=PE,∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,∴∠BPE=∠QPF,
又∵∠PEQ=∠PEB=90°,∴Rt△PQF≌Rt△PBE(ASA),
∴PB=PQ.
(第十八章《平行四边形》)
题 号 一 二 三 总 分
得 分
一、选择题(本大题共6个小题,每小题3分,共18分)
1.下列性质中,平行四边形不一定具备是( )
A.邻角互补 B.对角互补 C.对边相等 D.对角线互相平分
2.将一矩形纸条按如图所示折叠,则∠1的度数为( )
A.72° B.84° C.63° D.76°
3.已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
4.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )
A.3 B.4 C.5 D.6
如图,四边形是菱形,对角线,相交于点,,,点是上一动点,点是的中点,则的最小值为( )
A. B. C.3 D.
6.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
(
第6题
) (
第4题
)A.8 B.8 C.4 D.6
(
第2题
)
(
第5题
)
二、填空题(本大题共6个小题,每小题3分,满分18分)
7.过矩形ABCD的四个顶点作对角线AC,BD的平行线,分别相交于E,F,G,H四点,则四边形EFGH为 .
8.如图,在△ABC中,AB=6,BC=8,AC=4,D、E、F分别为BC、AC、AB中点,连接DE、FE,则四边形BDEF的周长是 .
9.如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知BC=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为 cm.
如图,在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的度数是 .
(
第
11
题
) (
第
10
题
) (
第
9
题
) (
第8题
)
11.如图,在矩形纸片ABCD中,AB=4,BC=8,将纸片折叠,使点C与点A重合,则折痕EF的长是 .
12.已知点A(2,2),B(﹣2,0),C(3,﹣1),且以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为: .
三、解答题(共64分)
13.(4分)如图所示,在平行四边形ABCD中,点E,F分别在边BC和AD上,且CE=AF,求证:△ABE ≌ △CDF.
14.(4分)如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,分别在图1、图2中按要求作图(保留作图痕迹,不这写作法).
(1)在图1中,在AB边上求作一点N,连接CN,使得CN=AM;
(2)在图2中,在AD边上求作一点Q,连接CQ,使得CQ=AM.
15.(6分)如图,在菱形ABCD中,∠A与∠B的度数比为1:2,周长是48.
(1)求两条对角线的长度.
(2)求菱形ABCD的面积.
(6分)在平行四边形ABCD中,点E、F是对角线AC上的两点,且AE=CF,求证:四边形BFDE是平行四边形.
(6分)如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,
且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
18.(6分)如图,如图,在中,点O是的中点,连接CO并延长交BA的延长线于点E,连接AC、DE.
(1)求证:四边形是平行四边形;
(2)若,判断四边形的形状,并说明理由.
19.(7分)如图,点O是△ABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若BO⊥CO,M为EF的中点,且OA=8,OM=3,
求四边形DEFG的周长.
20.(7分)如图, ABCD的对角线AC、BD相交于点,AB⊥AC,AB=3,BC=5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连结PO并延长交BC于点Q.设点P的运动时间为t秒.
(1)求BQ的长.(用含t的代数式表示)
(2)当四边形ABQP是平行四边形时,求t的值.
21.(8分)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AD=10,EC=4,求OE的长度.
22.(10分)如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
(三)
B 2.A 3.B 4.B 5.A 6.D
7.菱形 8.14 9.5 10.119° 11.
12.(﹣1,﹣3)或(﹣3,3)或(5,1)
13.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
∵CE=AF,∴AD-AF=BC-CE,即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS)
14.解:(1)如图1,CN即为所求.
(2)如图2,CQ即为所求.
15.(1)解:(1)∵菱形ABCD的周长是48cm,
∴AB=BC=CD=DA=12cm,
又∵∠ABC与∠BAD的度数比为1:2,∠ABC=60°,
∴△ABC是正三角形,AC=AB=12cm,又∠ABO=30°,
∴AO=6cm,BO=cm,BD=cm,
(2)∴S菱形ABCD=AC BD=cm2.
16.证明:如图,连接 交于
,
四边形是平行四边形.
17.解:(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.
18.(1)证明:在ABCD中,AB∥CD,∴,
∵点O为AD的中点,∴,
在与中,
∵,,,
∴,∴,
又∵BE∥CD ,∴四边形ACDE是平行四边形;
(2)解:由(1)知四边形ACDE是平行四边形,,
∵,∴,
∴四边形ACDE是菱形.
19.(1)证明:∵D、G分别是AB、AC的中点,
∴DG∥BC,DG=BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF=BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形;
(2)解:连接AO,
∵BO⊥CO,M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,∴DG=EF=6,
∵D是AB的中点,E是BO的中点,∴DE=AO=4,
∴四边形DEFG的周长为:4+4+6+6=20.
20.解:(1)四边形是平行四边形,
,,,
,≌,
,
,;
,
当时,四边形是平行四边形,
即,,
当为秒时,四边形是平行四边形.
21.(1)证明:∵四边形ABCD是菱形,∴AD∥BC且AD=BC,
∵BE=CF,∴BC=EF,∴AD=EF,
∵AD∥EF,∴四边形AEFD是平行四边形,
∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,AD=10,
∴AD=AB=BC=10,
∵EC=4,∴BE=10﹣4=6,
在Rt△ABE中,AE=,
在Rt△AEC中,AC=,
∵四边形ABCD是菱形,∴OA=OC,∴OE=AC=.
22.证明:过P作PE⊥BC于E,PF⊥CD于F,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,∴PF=PE,
∴四边形PECF为正方形,
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,∴∠BPE=∠QPF,
又∵∠PEQ=∠PEB=90°,∴Rt△PQF≌Rt△PBE(ASA),
∴PB=PQ;
(2)PB=PQ,
证明:过P作PE⊥BC延长线于E,PF⊥QD于F,
∵P,C为正方形对角线AC上的点,
∴PC平分∠ECF,∠DCB=90°,
∴PF=PE,∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,∴∠BPE=∠QPF,
又∵∠PEQ=∠PEB=90°,∴Rt△PQF≌Rt△PBE(ASA),
∴PB=PQ.
