24.2直线和圆的位置关系(2)
文档属性
| 名称 | 24.2直线和圆的位置关系(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 31.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-17 00:00:00 | ||
图片预览

文档简介
课型:新授 课题:24.2直线和圆的位置关系(2) 教材内容:直线和圆的位置关系(2)
学习提示:切线长定理,切线长定理的归纳与定理的应用。
学习之旅
备注
课前准备
①直线和圆的位置关系有_____________________;
②切线:______________________________________.
探究新知
看图填空:
①PA与⊙O有唯一的公共点,则PA与⊙O的位置关系是________ ;
②沿着直线PO将纸对折,
设圆上与点A重合的点为B,这时OB是⊙O的______,PB是⊙O的______,测量PA与PB的关系______,∠APO与∠BPO的关系_______.
巩固应用
如图:PA、PB是⊙O的两条切线,A、B为切点,直线PO交⊙O于点D、E,交AB于G,则
(1)图中互相垂直的线段有__________________.(只需写出一对线段),
(2)全等三角形有____________________________________,
相等的线段有______________________.
(3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.
2、从圆外一点可以作圆的______条切线,从圆上一点可以作圆的_____条切线,在圆内一点可以作圆的____条切线.
3、已知⊙O的半径为6cm,点P与圆的距离为12cm,经过点P作⊙O的两条切线,则这两条切线的夹角为____,切线长为______________cm。
4、思考:如图有一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
综合应用
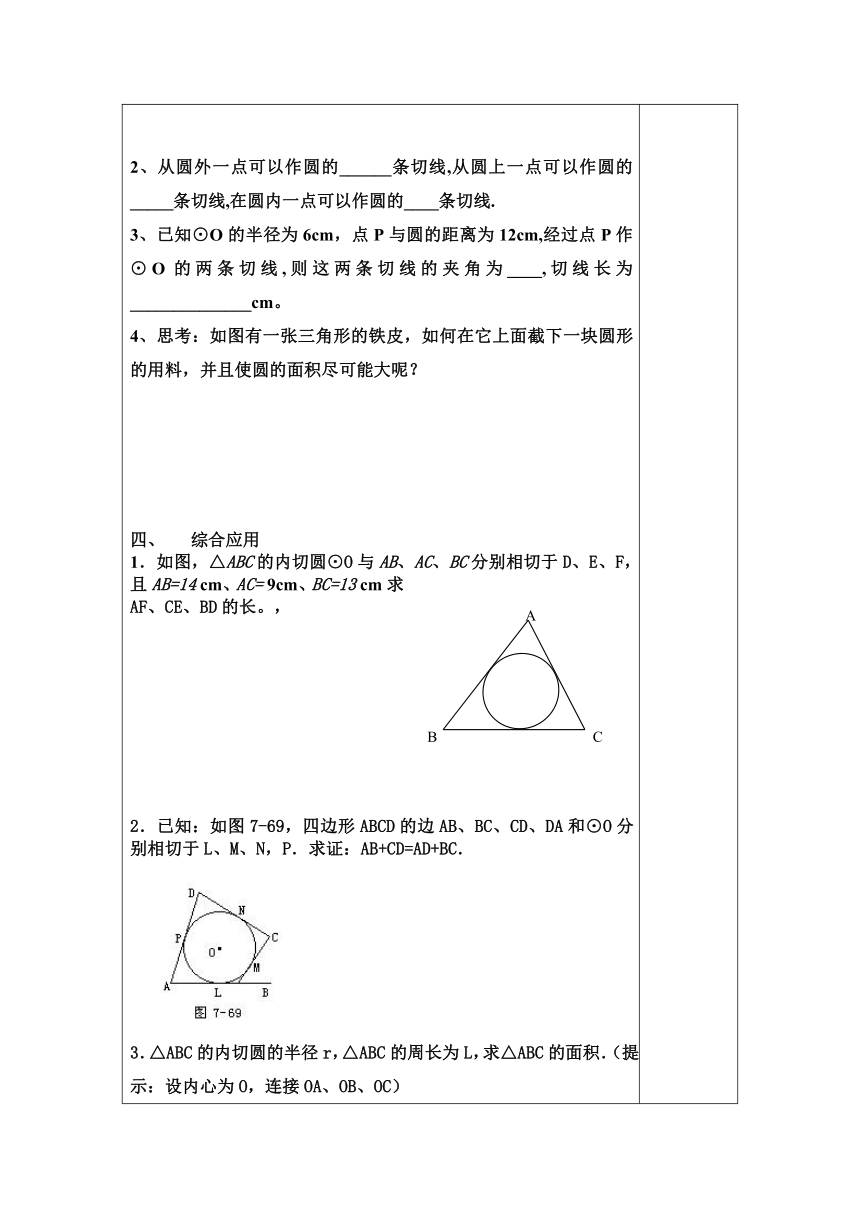
1.如图,△ABC的内切圆⊙O与AB、AC、BC分别相切于D、E、F,且AB=14 cm、AC= 9cm、BC=13 cm求AF、CE、BD的长。,
2.已知:如图7-69,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于L、M、N,P.求证:AB+CD=AD+BC.
3.△ABC的内切圆的半径r,△ABC的周长为L,求△ABC的面积.(提示:设内心为O,连接OA、OB、OC)
课堂检测
(一)选择题.
1.如图1,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ).
A.60° B.75° C.105° D.120°
(1) (2) (3) (4)
2.从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( ).
A.9 B.9(-1) C.9(-1) D.9
3.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )
A.180°-a B.90°-a C.90°+a D.180°-2a
(二)、填空题
1.如图2,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________.
2.如图3,边长为a的正三角形的内切圆半径是_________.
3.如图4,圆O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.
4、直角三角形的两直角边分别是5cm, 12cm 则其内切圆的半径为______。
5、⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过点P和⊙O的两条切线,则这两条切线的夹角是_____,切线长_____________.
6、如图5,⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O于P点,交AB、BC于E、F,则△BEF的周长是_____.
7、已知:P为⊙O外一点,PA、PB为⊙O的切线,A和B是切点,BC是直径.
求证:AC∥OP.
8、已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.
自主学习反思:
课型:新授 课题:24.2直线和圆的位置关系(2) 教材内容:直线和圆的位置关系(2)
学习提示:切线长定理,切线长定理的归纳与定理的应用。
学习之旅
备注
课前准备
①直线和圆的位置关系有_____________________;
②切线:______________________________________.
探究新知
看图填空:
①PA与⊙O有唯一的公共点,则PA与⊙O的位置关系是________ ;
②沿着直线PO将纸对折,
设圆上与点A重合的点为B,这时OB是⊙O的______,PB是⊙O的______,测量PA与PB的关系______,∠APO与∠BPO的关系_______.
巩固应用
如图:PA、PB是⊙O的两条切线,A、B为切点,直线PO交⊙O于点D、E,交AB于G,则
(1)图中互相垂直的线段有__________________.(只需写出一对线段),
(2)全等三角形有____________________________________,
相等的线段有______________________.
(3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.
2、从圆外一点可以作圆的______条切线,从圆上一点可以作圆的_____条切线,在圆内一点可以作圆的____条切线.
3、已知⊙O的半径为6cm,点P与圆的距离为12cm,经过点P作⊙O的两条切线,则这两条切线的夹角为____,切线长为______________cm。
4、思考:如图有一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
综合应用
1.如图,△ABC的内切圆⊙O与AB、AC、BC分别相切于D、E、F,且AB=14 cm、AC= 9cm、BC=13 cm求AF、CE、BD的长。,
2.已知:如图7-69,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于L、M、N,P.求证:AB+CD=AD+BC.
3.△ABC的内切圆的半径r,△ABC的周长为L,求△ABC的面积.(提示:设内心为O,连接OA、OB、OC)
课堂检测
(一)选择题.
1.如图1,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ).
A.60° B.75° C.105° D.120°
(1) (2) (3) (4)
2.从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( ).
A.9 B.9(-1) C.9(-1) D.9
3.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )
A.180°-a B.90°-a C.90°+a D.180°-2a
(二)、填空题
1.如图2,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________.
2.如图3,边长为a的正三角形的内切圆半径是_________.
3.如图4,圆O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.
4、直角三角形的两直角边分别是5cm, 12cm 则其内切圆的半径为______。
5、⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过点P和⊙O的两条切线,则这两条切线的夹角是_____,切线长_____________.
6、如图5,⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O于P点,交AB、BC于E、F,则△BEF的周长是_____.
7、已知:P为⊙O外一点,PA、PB为⊙O的切线,A和B是切点,BC是直径.
求证:AC∥OP.
8、已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.
自主学习反思:
学习提示:切线长定理,切线长定理的归纳与定理的应用。
学习之旅
备注
课前准备
①直线和圆的位置关系有_____________________;
②切线:______________________________________.
探究新知
看图填空:
①PA与⊙O有唯一的公共点,则PA与⊙O的位置关系是________ ;
②沿着直线PO将纸对折,
设圆上与点A重合的点为B,这时OB是⊙O的______,PB是⊙O的______,测量PA与PB的关系______,∠APO与∠BPO的关系_______.
巩固应用
如图:PA、PB是⊙O的两条切线,A、B为切点,直线PO交⊙O于点D、E,交AB于G,则
(1)图中互相垂直的线段有__________________.(只需写出一对线段),
(2)全等三角形有____________________________________,
相等的线段有______________________.
(3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.
2、从圆外一点可以作圆的______条切线,从圆上一点可以作圆的_____条切线,在圆内一点可以作圆的____条切线.
3、已知⊙O的半径为6cm,点P与圆的距离为12cm,经过点P作⊙O的两条切线,则这两条切线的夹角为____,切线长为______________cm。
4、思考:如图有一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
综合应用
1.如图,△ABC的内切圆⊙O与AB、AC、BC分别相切于D、E、F,且AB=14 cm、AC= 9cm、BC=13 cm求AF、CE、BD的长。,
2.已知:如图7-69,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于L、M、N,P.求证:AB+CD=AD+BC.
3.△ABC的内切圆的半径r,△ABC的周长为L,求△ABC的面积.(提示:设内心为O,连接OA、OB、OC)
课堂检测
(一)选择题.
1.如图1,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ).
A.60° B.75° C.105° D.120°
(1) (2) (3) (4)
2.从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( ).
A.9 B.9(-1) C.9(-1) D.9
3.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )
A.180°-a B.90°-a C.90°+a D.180°-2a
(二)、填空题
1.如图2,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________.
2.如图3,边长为a的正三角形的内切圆半径是_________.
3.如图4,圆O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.
4、直角三角形的两直角边分别是5cm, 12cm 则其内切圆的半径为______。
5、⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过点P和⊙O的两条切线,则这两条切线的夹角是_____,切线长_____________.
6、如图5,⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O于P点,交AB、BC于E、F,则△BEF的周长是_____.
7、已知:P为⊙O外一点,PA、PB为⊙O的切线,A和B是切点,BC是直径.
求证:AC∥OP.
8、已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.
自主学习反思:
课型:新授 课题:24.2直线和圆的位置关系(2) 教材内容:直线和圆的位置关系(2)
学习提示:切线长定理,切线长定理的归纳与定理的应用。
学习之旅
备注
课前准备
①直线和圆的位置关系有_____________________;
②切线:______________________________________.
探究新知
看图填空:
①PA与⊙O有唯一的公共点,则PA与⊙O的位置关系是________ ;
②沿着直线PO将纸对折,
设圆上与点A重合的点为B,这时OB是⊙O的______,PB是⊙O的______,测量PA与PB的关系______,∠APO与∠BPO的关系_______.
巩固应用
如图:PA、PB是⊙O的两条切线,A、B为切点,直线PO交⊙O于点D、E,交AB于G,则
(1)图中互相垂直的线段有__________________.(只需写出一对线段),
(2)全等三角形有____________________________________,
相等的线段有______________________.
(3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.
2、从圆外一点可以作圆的______条切线,从圆上一点可以作圆的_____条切线,在圆内一点可以作圆的____条切线.
3、已知⊙O的半径为6cm,点P与圆的距离为12cm,经过点P作⊙O的两条切线,则这两条切线的夹角为____,切线长为______________cm。
4、思考:如图有一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
综合应用
1.如图,△ABC的内切圆⊙O与AB、AC、BC分别相切于D、E、F,且AB=14 cm、AC= 9cm、BC=13 cm求AF、CE、BD的长。,
2.已知:如图7-69,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于L、M、N,P.求证:AB+CD=AD+BC.
3.△ABC的内切圆的半径r,△ABC的周长为L,求△ABC的面积.(提示:设内心为O,连接OA、OB、OC)
课堂检测
(一)选择题.
1.如图1,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ).
A.60° B.75° C.105° D.120°
(1) (2) (3) (4)
2.从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( ).
A.9 B.9(-1) C.9(-1) D.9
3.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )
A.180°-a B.90°-a C.90°+a D.180°-2a
(二)、填空题
1.如图2,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________.
2.如图3,边长为a的正三角形的内切圆半径是_________.
3.如图4,圆O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.
4、直角三角形的两直角边分别是5cm, 12cm 则其内切圆的半径为______。
5、⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过点P和⊙O的两条切线,则这两条切线的夹角是_____,切线长_____________.
6、如图5,⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O于P点,交AB、BC于E、F,则△BEF的周长是_____.
7、已知:P为⊙O外一点,PA、PB为⊙O的切线,A和B是切点,BC是直径.
求证:AC∥OP.
8、已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.
自主学习反思:
同课章节目录
