图形的相似(2)
图片预览




文档简介
课件23张PPT。图形的相似(2) 第二十七章 相似复习1、图中的正△A1B1C1是由正△ABC放
大后得到的,这两个三角形有什么关
系?放大CABC1A1B1正△A1B2C3与正△ABC相似复习2、图中是两个正六边形,它们有什么
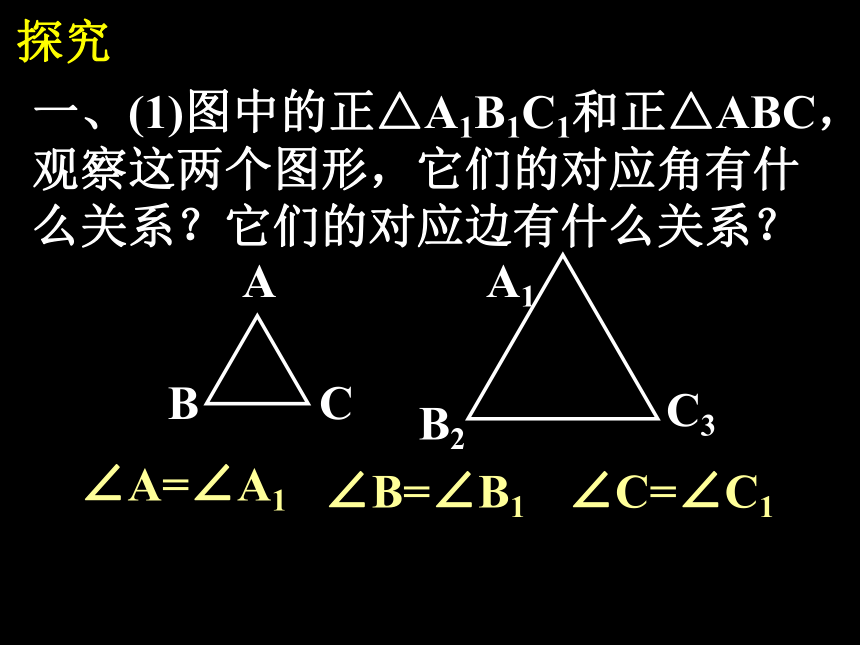
关系?两个正六边形相似缩小探究一、(1)图中的正△A1B1C1和正△ABC,
观察这两个图形,它们的对应角有什
么关系?它们的对应边有什么关系?
CABC3A1B2∠C=∠C1∠A=∠A1∠B=∠B1探究一、(2)图中的两个正六边形,观察这
两个图形,它们的对应角有什么关系?对应边有什么关系?
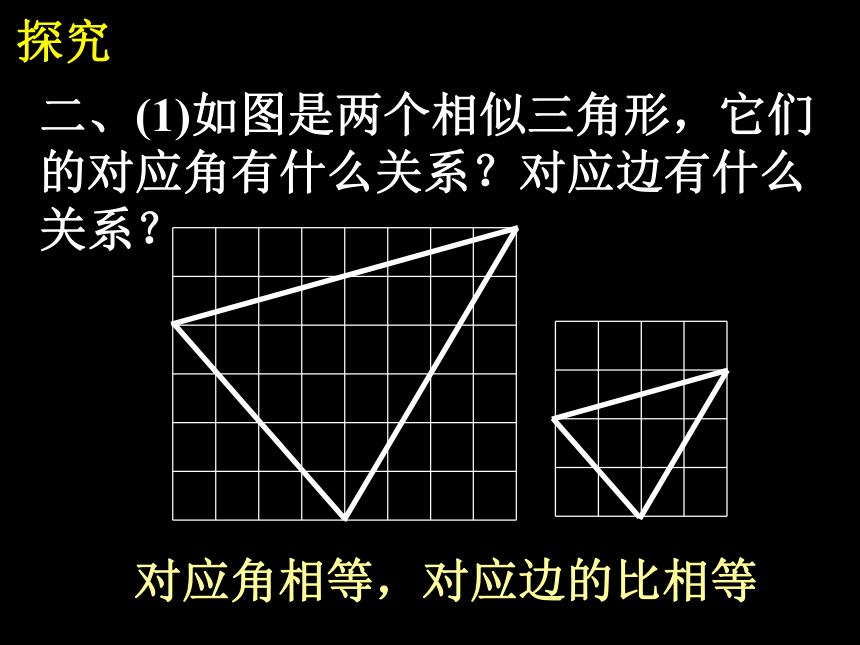
对应角相等对应边的比相等二、(1)如图是两个相似三角形,它们
的对应角有什么关系?对应边有什么
关系?探究对应角相等,对应边的比相等三、(2)如图是两个相似四边形,它们
的对应角有什么关系?对应边有什么
关系?探究对应角相等,对应边的比相等归纳相似多边形的性质: 相似多边形的对应角相等,对应边的比相等。例1下列说法正确的是( ) A.所有的平行四边形都相似
B.所有的矩形都相似 C.所有的菱形都相似
D.所有的正方形都相似 范例例2、如图,四边形ABCD和EFGH相似,求角α、β的大小和EH的长度x。21cm24cm18cm83°78°βαx118°巩固2、如图,△ABC与△DEF相似。
求未知边x、y的长度。 CABFDE48712xy巩固3、如图所示的两个五边形相似,求未
知边a、b、c的长度。5327.569cdba例3(补充)
已知四边形ABCD与四边形A1B1C1D1相似,A1B1:B1C1:C1D1:D1A1=7:8:11:14,若四边形ABCD的周长为40,求四边形ABCD的各边的长. 如图是两个相似多边形,它们的
对应边的比分别是多少?新授21cm24cm18cmx(相似比)归纳相似比的意义: 相似多边形对应边的比值为k,则
k就叫相似比。 如图是两个相似三角形:新授 如果相似比k=1,两个三角形有怎
样的关系?归纳相似比的意义: 相似多边形对应边的比值为k,则
k就叫相似比。 如果相似比k=1,那么多边形是全
等多边形。巩固4、在比例尺为1∶10 000 000的地图上,
量得甲、乙两地的距离是30cm,求两
地的实际距离。怎样理解“比例尺为1∶100 00 000”?相似比k为1∶100 00 000四、如图是两个多边形,它们的对应
角相等,对应边的比相等,这两个多
边形有什么关系?探究四边形ABCD与四边形A’B’C’D’相似归纳相似多边形的判定: 如果两个多边形满足对应角相等,
对应边的比相等,那么这两个多边形
相似。范例例2、如图,DE∥BC,求 、 、 ,并证明△ADE∽△ABC。巩固6、如图所示的两个三角形相似吗?
为什么?551010小结1.相似多边形的性质: 相似多边形的对应角相等,对应
边的比相等。2.相似多边形的判定: 如果两个多边形满足对应角相等,
对应边的比相等,那么这两个多边形
相似。
大后得到的,这两个三角形有什么关
系?放大CABC1A1B1正△A1B2C3与正△ABC相似复习2、图中是两个正六边形,它们有什么
关系?两个正六边形相似缩小探究一、(1)图中的正△A1B1C1和正△ABC,
观察这两个图形,它们的对应角有什
么关系?它们的对应边有什么关系?
CABC3A1B2∠C=∠C1∠A=∠A1∠B=∠B1探究一、(2)图中的两个正六边形,观察这
两个图形,它们的对应角有什么关系?对应边有什么关系?
对应角相等对应边的比相等二、(1)如图是两个相似三角形,它们
的对应角有什么关系?对应边有什么
关系?探究对应角相等,对应边的比相等三、(2)如图是两个相似四边形,它们
的对应角有什么关系?对应边有什么
关系?探究对应角相等,对应边的比相等归纳相似多边形的性质: 相似多边形的对应角相等,对应边的比相等。例1下列说法正确的是( ) A.所有的平行四边形都相似
B.所有的矩形都相似 C.所有的菱形都相似
D.所有的正方形都相似 范例例2、如图,四边形ABCD和EFGH相似,求角α、β的大小和EH的长度x。21cm24cm18cm83°78°βαx118°巩固2、如图,△ABC与△DEF相似。
求未知边x、y的长度。 CABFDE48712xy巩固3、如图所示的两个五边形相似,求未
知边a、b、c的长度。5327.569cdba例3(补充)
已知四边形ABCD与四边形A1B1C1D1相似,A1B1:B1C1:C1D1:D1A1=7:8:11:14,若四边形ABCD的周长为40,求四边形ABCD的各边的长. 如图是两个相似多边形,它们的
对应边的比分别是多少?新授21cm24cm18cmx(相似比)归纳相似比的意义: 相似多边形对应边的比值为k,则
k就叫相似比。 如图是两个相似三角形:新授 如果相似比k=1,两个三角形有怎
样的关系?归纳相似比的意义: 相似多边形对应边的比值为k,则
k就叫相似比。 如果相似比k=1,那么多边形是全
等多边形。巩固4、在比例尺为1∶10 000 000的地图上,
量得甲、乙两地的距离是30cm,求两
地的实际距离。怎样理解“比例尺为1∶100 00 000”?相似比k为1∶100 00 000四、如图是两个多边形,它们的对应
角相等,对应边的比相等,这两个多
边形有什么关系?探究四边形ABCD与四边形A’B’C’D’相似归纳相似多边形的判定: 如果两个多边形满足对应角相等,
对应边的比相等,那么这两个多边形
相似。范例例2、如图,DE∥BC,求 、 、 ,并证明△ADE∽△ABC。巩固6、如图所示的两个三角形相似吗?
为什么?551010小结1.相似多边形的性质: 相似多边形的对应角相等,对应
边的比相等。2.相似多边形的判定: 如果两个多边形满足对应角相等,
对应边的比相等,那么这两个多边形
相似。
