北师大版小学六年级数学下册《圆柱与圆锥》练习(含答案)
文档属性
| 名称 | 北师大版小学六年级数学下册《圆柱与圆锥》练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 814.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览


文档简介
圆柱与圆锥
一、填空题。
1.下图是一块长方形铁皮(每个小方格的边长是1dm),剪下图中的阴影部分可以围成一个圆柱。围成的这个圆柱的表面积是( )dm ,体积是( )dm 。
2.一个圆柱,它的底面直径是4cm,高是6cm,这个圆柱的体积是( )cm ,与它等底等高的圆锥的体积是( )cm 。
3.一个圆锥的底面直径与高相等,它的底面周长是9.42dm。这个圆锥的体积是
( )dm 。
4.两个底面积相等的圆柱,一个高是4.5cm,体积是81cm ;另一个高是3cm,体积是( )cm 。
5.把一个底面半径是2cm,高是1.5cm的圆柱形钢铁,铸成与它底面积相等的圆锥形钢锭。这个圆锥形钢锭的体积是( )cm ,高是( )cm。
6.一根长4m、底面直径为20dm的圆柱形木料,平均截成5段,表面积增加了( )dm ,每段木料的体积是( )dm 。
7.如图,把直角三角形以一条直角边为轴快速旋转一周,得到的圆锥体积最大是( )cm 。
8.已知图中的圆柱形和圆锥形容器的底面积和高都相等(如图),张老师把2L水倒入这两个容器里,刚好都倒满。圆柱形容器的容积是( )L。
9.一根自来水水管的内直径是2cm,水管内水的流速是每秒8cm。一位同学去洗手,走时忘记关掉水龙头,5分会浪费( )L的水。
10.我们在研究圆柱的体积公式时,是将一个圆柱转化成长方体得出的。如果将转化得到的长方体翻转一下摆放(如图)。
观察上图,我们发现翻转后长方体的底面积等于圆柱的( ),长方体的高等
于圆柱的( );如果这个圆柱的侧面积是18.84dm ,底面直径是6dm,它的体积是( )dm 。
二、判断题
1.两个圆柱的侧面积相等,它们的表面积也一定相等。 ( )
2.圆柱有无数条高,而圆锥只有一条高。 ( )
3.一个圆柱的侧面展开图是一个正方形,它的高定是底面直径的π倍。( )
4.如果一个圆锥的体积是一个圆柱体积的,那么它们一定等底等高 。( )
5.长方体、正方体、圆柱和圆锥的体积都是用公式“底面积×高”来进行计算的。( )
6.一个圆柱的底面半径和高都扩大为原来的5倍,则它的体积就扩大为原来的25倍。 ( )
三、选择题
1.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是15dm ,圆柱的体积是( )dm 。
A.45 B.15 C.5
2.甲圆柱体的底面直径是6cm,高是10cm;乙圆柱体的底面直径是10cm,高是6cm。那么比较它们的表面积知( )
A.甲>乙 B.甲=乙 C.甲<乙
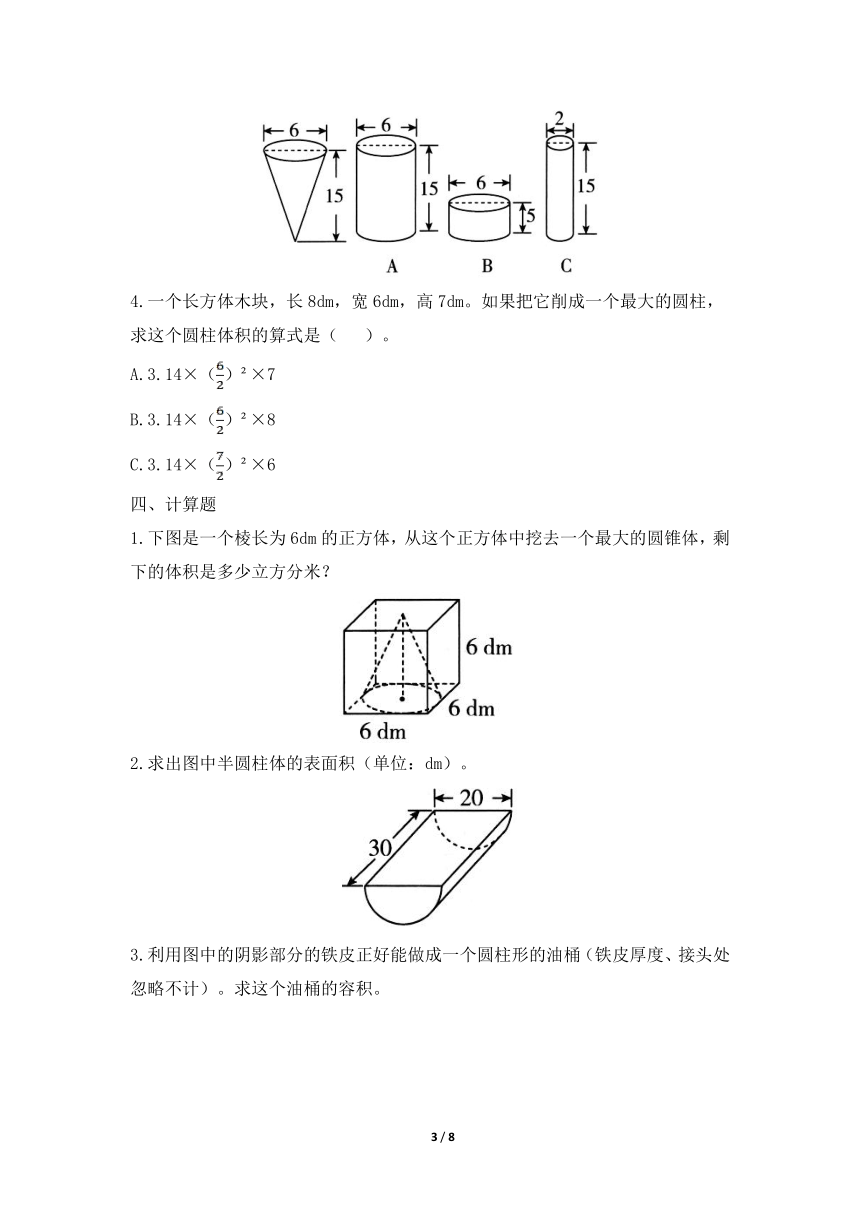
3.在如下左图圆锥形玻璃容器内装满水,将这些水倒入( )号圆柱形容器中正好装满。(单位:cm,玻璃容器厚度忽略不计)
4.一个长方体木块,长8dm,宽6dm,高7dm。如果把它削成一个最大的圆柱,求这个圆柱体积的算式是( )。
A.3.14×() ×7
B.3.14×() ×8
C.3.14×( QUOTE QUOTE ) ×6
四、计算题
1.下图是一个棱长为6dm的正方体,从这个正方体中挖去一个最大的圆锥体,剩下的体积是多少立方分米?
2.求出图中半圆柱体的表面积(单位:dm)。
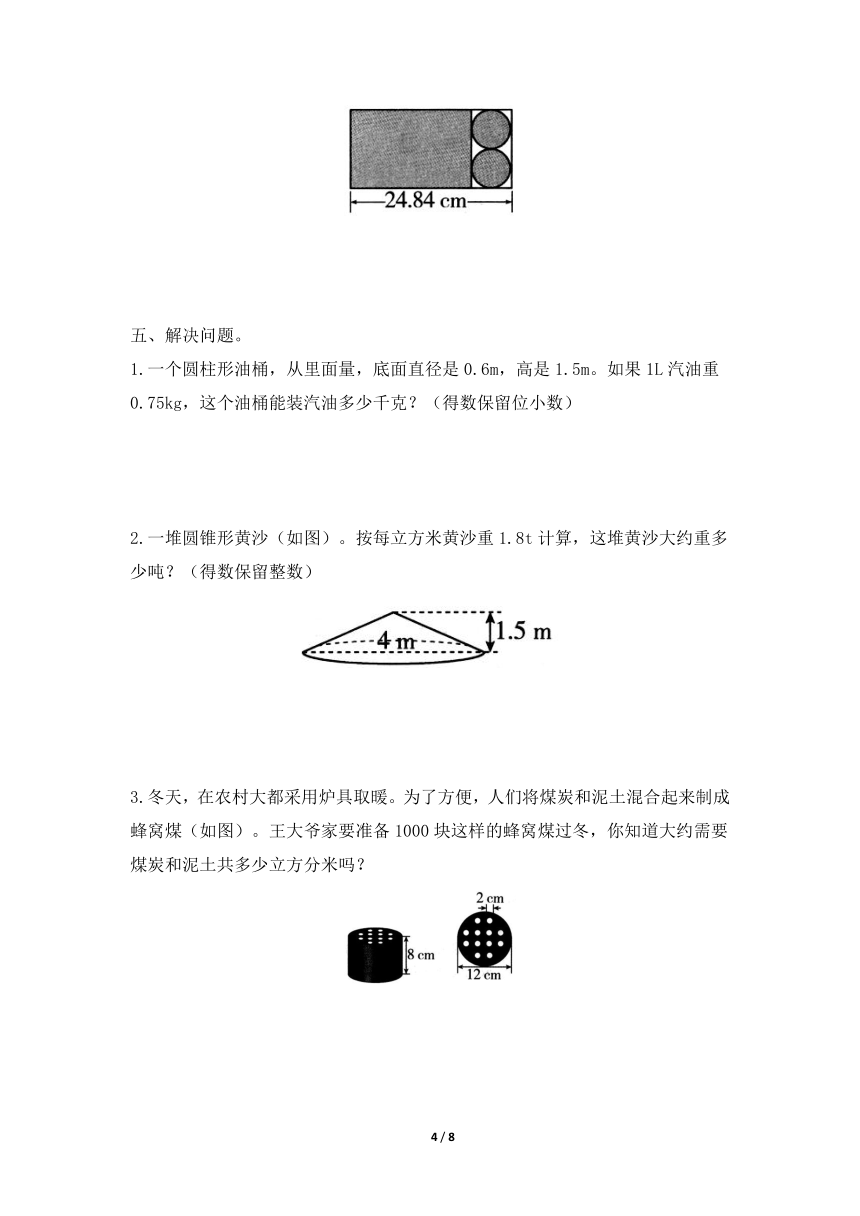
3.利用图中的阴影部分的铁皮正好能做成一个圆柱形的油桶(铁皮厚度、接头处忽略不计)。求这个油桶的容积。
五、解决问题。
1.一个圆柱形油桶,从里面量,底面直径是0.6m,高是1.5m。如果1L汽油重0.75kg,这个油桶能装汽油多少千克?(得数保留位小数)
2.一堆圆锥形黄沙(如图)。按每立方米黄沙重1.8t计算,这堆黄沙大约重多少吨?(得数保留整数)
3.冬天,在农村大都采用炉具取暖。为了方便,人们将煤炭和泥土混合起来制成蜂窝煤(如图)。王大爷家要准备1000块这样的蜂窝煤过冬,你知道大约需要煤炭和泥土共多少立方分米吗?
4.把3个高相等、底面半径都是10cm的圆柱形盒子叠放在一起(如图)。拿走1个盒子,表面积就减少314cm 。每个盒子的体积是多少立方厘米?
5.如图,这个工具箱的下半部分是一个棱长为2dm的正方体,上半部分是一个半圆柱。这个工具箱的表面积是多少平方分米?体积是多少立方分米?
6.一个圆柱和一个圆锥等底等高,它们的体积相差50.24cm 。如果圆柱的底面半径是2cm,这个圆柱的侧面积是多少平方厘米?
7.现有两根同样的圆柱形木材(如图),王师傅把其中一根加工成一个最大的长方体,把另一根加工成一个最大的圆锥。加工成的长方体和圆锥相比较,谁的体积大?大多少立方分米?
8.如图所示,把一个底面半径是10cm,高是25cm的圆柱形木料沿高切去后,求剩下部分的表面积和体积。
参考答案
一、1.18.84 6.28
2.75.36 25.12
3.7.065
4.54
5.18.84 4.5
6.2512 2512
7.50.24
8.1.5
9.7.536
10.侧面积的一半 底面半径 28.26
二、1.×2.√3.√4.×5.×6.×
三、1.B 2.C 3.B 4.C
四、1.6×6×6-3.14×(6÷2) ×6×=159.48(dm )
2.3.14×(20÷2) +30×20+3.14×20×30÷2=1856(dm )
提示:这个半圆柱体的表面积2个半圆的面积的和(1个圆的面积)+1个长方形的面积+圆柱侧面积的一半。
3.24.84÷(3.14+1)=6(cm) 3.14×(6÷2) ×(6×2)=339.12(cm )
339.12cm =339.12mL
提示:根据题图可知,阴影部分的长方形的长就是圆柱形油桶的底面周长,宽就是圆柱的高(也就是两条底面直径的长度和)。24.84cm就是底面周长与一条直径长的和,即πd+d=(π+1)d=24.84。先求出圆柱形油桶的底面直径和高,再求它的容积。
五、1.0.6m=6dm 1.5m=15dm
3.14×(6÷2) ×15=423.9(dm)
423.9dm =423.9L 423.9×0.75≈317.9(kg)
2.3.14×(4÷2) ×1.5××1.8≈11(t)
3.314×(12÷2) ×8-3.14×(2÷2) ×8×12=602.88(cm )
602.88×1000=602880(cm )
602880cm =602.88dm
4.314÷(3.14×10×2)=5(cm) 3.14×10 ×5=1570(cm )
提示:减少的314cm 就是1个盒子的侧面积,先求出每个盒子的高,再求每个盒子的体积。
5.2×2×5+3.14×(2÷2) +3.14×2×2÷2=29.42(dm )
2×2×2+3.14×(2÷2) ×2÷2=11.14(dm )
提示:这个工具箱的表面积=正方体5个面的面积的和+2个半圆的面积的和(1个圆的面积)+圆柱侧面积的一半,这个工具箱的体积=正方体的体积+圆柱体积的一半。
6.50.24÷2×3÷(3.14×2 )=6(cm) 3.14×2×2×6=75.36(cm )
7.长方体的体积:2×2÷2×3=6(dm )
圆锥体的体积:3.14×(2÷2) ×3×=3.14(dm )
体积之差:6-3.14=2.86(dm )
加工成的长方体的体积大,大2.86dm 。
提示:加工成的长方体的底面是正方形,正方形的对角线的长是2dm(如图)。把正方形沿一条对角线剪成两个完全一样的等腰三角形,再把这两个三角形拼成一个两条直角边都是2dm的等腰直角三角形,则长方体的底面积为2×2÷2=2(dm ),求出了长方体的底面积,就很容易求出长方体的体积。
8.1-= 3.14×10 ××2+3.14×10×2×25×+10×25×2=2148.5(cm ) 3.14×10 ×25×=5887.5(cm )
提示:剩下部分的表面积=2个圆的面积的和+圆柱侧面积的+2个长方形的面积,剩下部分的体积=圆柱的体积×。
5 / 9
一、填空题。
1.下图是一块长方形铁皮(每个小方格的边长是1dm),剪下图中的阴影部分可以围成一个圆柱。围成的这个圆柱的表面积是( )dm ,体积是( )dm 。
2.一个圆柱,它的底面直径是4cm,高是6cm,这个圆柱的体积是( )cm ,与它等底等高的圆锥的体积是( )cm 。
3.一个圆锥的底面直径与高相等,它的底面周长是9.42dm。这个圆锥的体积是
( )dm 。
4.两个底面积相等的圆柱,一个高是4.5cm,体积是81cm ;另一个高是3cm,体积是( )cm 。
5.把一个底面半径是2cm,高是1.5cm的圆柱形钢铁,铸成与它底面积相等的圆锥形钢锭。这个圆锥形钢锭的体积是( )cm ,高是( )cm。
6.一根长4m、底面直径为20dm的圆柱形木料,平均截成5段,表面积增加了( )dm ,每段木料的体积是( )dm 。
7.如图,把直角三角形以一条直角边为轴快速旋转一周,得到的圆锥体积最大是( )cm 。
8.已知图中的圆柱形和圆锥形容器的底面积和高都相等(如图),张老师把2L水倒入这两个容器里,刚好都倒满。圆柱形容器的容积是( )L。
9.一根自来水水管的内直径是2cm,水管内水的流速是每秒8cm。一位同学去洗手,走时忘记关掉水龙头,5分会浪费( )L的水。
10.我们在研究圆柱的体积公式时,是将一个圆柱转化成长方体得出的。如果将转化得到的长方体翻转一下摆放(如图)。
观察上图,我们发现翻转后长方体的底面积等于圆柱的( ),长方体的高等
于圆柱的( );如果这个圆柱的侧面积是18.84dm ,底面直径是6dm,它的体积是( )dm 。
二、判断题
1.两个圆柱的侧面积相等,它们的表面积也一定相等。 ( )
2.圆柱有无数条高,而圆锥只有一条高。 ( )
3.一个圆柱的侧面展开图是一个正方形,它的高定是底面直径的π倍。( )
4.如果一个圆锥的体积是一个圆柱体积的,那么它们一定等底等高 。( )
5.长方体、正方体、圆柱和圆锥的体积都是用公式“底面积×高”来进行计算的。( )
6.一个圆柱的底面半径和高都扩大为原来的5倍,则它的体积就扩大为原来的25倍。 ( )
三、选择题
1.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是15dm ,圆柱的体积是( )dm 。
A.45 B.15 C.5
2.甲圆柱体的底面直径是6cm,高是10cm;乙圆柱体的底面直径是10cm,高是6cm。那么比较它们的表面积知( )
A.甲>乙 B.甲=乙 C.甲<乙
3.在如下左图圆锥形玻璃容器内装满水,将这些水倒入( )号圆柱形容器中正好装满。(单位:cm,玻璃容器厚度忽略不计)
4.一个长方体木块,长8dm,宽6dm,高7dm。如果把它削成一个最大的圆柱,求这个圆柱体积的算式是( )。
A.3.14×() ×7
B.3.14×() ×8
C.3.14×( QUOTE QUOTE ) ×6
四、计算题
1.下图是一个棱长为6dm的正方体,从这个正方体中挖去一个最大的圆锥体,剩下的体积是多少立方分米?
2.求出图中半圆柱体的表面积(单位:dm)。
3.利用图中的阴影部分的铁皮正好能做成一个圆柱形的油桶(铁皮厚度、接头处忽略不计)。求这个油桶的容积。
五、解决问题。
1.一个圆柱形油桶,从里面量,底面直径是0.6m,高是1.5m。如果1L汽油重0.75kg,这个油桶能装汽油多少千克?(得数保留位小数)
2.一堆圆锥形黄沙(如图)。按每立方米黄沙重1.8t计算,这堆黄沙大约重多少吨?(得数保留整数)
3.冬天,在农村大都采用炉具取暖。为了方便,人们将煤炭和泥土混合起来制成蜂窝煤(如图)。王大爷家要准备1000块这样的蜂窝煤过冬,你知道大约需要煤炭和泥土共多少立方分米吗?
4.把3个高相等、底面半径都是10cm的圆柱形盒子叠放在一起(如图)。拿走1个盒子,表面积就减少314cm 。每个盒子的体积是多少立方厘米?
5.如图,这个工具箱的下半部分是一个棱长为2dm的正方体,上半部分是一个半圆柱。这个工具箱的表面积是多少平方分米?体积是多少立方分米?
6.一个圆柱和一个圆锥等底等高,它们的体积相差50.24cm 。如果圆柱的底面半径是2cm,这个圆柱的侧面积是多少平方厘米?
7.现有两根同样的圆柱形木材(如图),王师傅把其中一根加工成一个最大的长方体,把另一根加工成一个最大的圆锥。加工成的长方体和圆锥相比较,谁的体积大?大多少立方分米?
8.如图所示,把一个底面半径是10cm,高是25cm的圆柱形木料沿高切去后,求剩下部分的表面积和体积。
参考答案
一、1.18.84 6.28
2.75.36 25.12
3.7.065
4.54
5.18.84 4.5
6.2512 2512
7.50.24
8.1.5
9.7.536
10.侧面积的一半 底面半径 28.26
二、1.×2.√3.√4.×5.×6.×
三、1.B 2.C 3.B 4.C
四、1.6×6×6-3.14×(6÷2) ×6×=159.48(dm )
2.3.14×(20÷2) +30×20+3.14×20×30÷2=1856(dm )
提示:这个半圆柱体的表面积2个半圆的面积的和(1个圆的面积)+1个长方形的面积+圆柱侧面积的一半。
3.24.84÷(3.14+1)=6(cm) 3.14×(6÷2) ×(6×2)=339.12(cm )
339.12cm =339.12mL
提示:根据题图可知,阴影部分的长方形的长就是圆柱形油桶的底面周长,宽就是圆柱的高(也就是两条底面直径的长度和)。24.84cm就是底面周长与一条直径长的和,即πd+d=(π+1)d=24.84。先求出圆柱形油桶的底面直径和高,再求它的容积。
五、1.0.6m=6dm 1.5m=15dm
3.14×(6÷2) ×15=423.9(dm)
423.9dm =423.9L 423.9×0.75≈317.9(kg)
2.3.14×(4÷2) ×1.5××1.8≈11(t)
3.314×(12÷2) ×8-3.14×(2÷2) ×8×12=602.88(cm )
602.88×1000=602880(cm )
602880cm =602.88dm
4.314÷(3.14×10×2)=5(cm) 3.14×10 ×5=1570(cm )
提示:减少的314cm 就是1个盒子的侧面积,先求出每个盒子的高,再求每个盒子的体积。
5.2×2×5+3.14×(2÷2) +3.14×2×2÷2=29.42(dm )
2×2×2+3.14×(2÷2) ×2÷2=11.14(dm )
提示:这个工具箱的表面积=正方体5个面的面积的和+2个半圆的面积的和(1个圆的面积)+圆柱侧面积的一半,这个工具箱的体积=正方体的体积+圆柱体积的一半。
6.50.24÷2×3÷(3.14×2 )=6(cm) 3.14×2×2×6=75.36(cm )
7.长方体的体积:2×2÷2×3=6(dm )
圆锥体的体积:3.14×(2÷2) ×3×=3.14(dm )
体积之差:6-3.14=2.86(dm )
加工成的长方体的体积大,大2.86dm 。
提示:加工成的长方体的底面是正方形,正方形的对角线的长是2dm(如图)。把正方形沿一条对角线剪成两个完全一样的等腰三角形,再把这两个三角形拼成一个两条直角边都是2dm的等腰直角三角形,则长方体的底面积为2×2÷2=2(dm ),求出了长方体的底面积,就很容易求出长方体的体积。
8.1-= 3.14×10 ××2+3.14×10×2×25×+10×25×2=2148.5(cm ) 3.14×10 ×25×=5887.5(cm )
提示:剩下部分的表面积=2个圆的面积的和+圆柱侧面积的+2个长方形的面积,剩下部分的体积=圆柱的体积×。
5 / 9
