北师大版小学六年级数学下册《第1单元达标作业》(带答案)
文档属性
| 名称 | 北师大版小学六年级数学下册《第1单元达标作业》(带答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览


文档简介
第1单元达标作业
1.选一选。(将正确答案前的字母填在括号里)
(1)把一个圆柱的侧面展开,不可能得到下面的( )图形。
A. B. C.
(2)已知一个正方体的底面周长和一个圆柱的底面周长相等,它们的高也相等。它们的表面积相比,( )。
A.相等
B.正方体的表面积大于圆柱的表面积
C.正方体的表面积小于圆柱的表面积
(3)用一张长6厘米、宽2厘米的长方形纸卷成一个圆柱,按( )的方式卷,得到的圆柱体积最大。
A.以2厘米作为圆柱的高
B.以6厘米作为圆柱的高
C.无论哪种
(4)一个圆柱和一个圆锥的高和体积分别相等,那么圆柱的底面积是圆锥底面积的( )。
A.3倍 B. C.
2.认真想,仔细填。
(1)
图形 底面半径 底面直径 高 表面积 体积
圆柱 2 cm 5cm
10dm 8dm
圆锥 4.8m 10m ——
0.6m 1.2m ——
(2)要制作一个无盖圆柱形水桶,有以下四种型号的铁皮可供搭配选择。(铁皮不可切割)
① ② ③ ④
你选择的是( )号和( )号,用你选择的材料制作的水桶表面积是( )平方分米。
(3)张师傅要把一根底面直径10cm、高27cm的圆柱形木料削成一个最大的圆锥,削去的木料体积是( )立方厘米。
3.有两个棱长都是10cm的正方体木块A和B。用正方体木块A削一个底面直径8cm、高10cm的圆柱;用正方体木块B削4个底面直径5cm、高10cm的圆柱。剩下的木料哪个多,多多少?(请用计算过程说明理由)
4.一个圆柱形钢坯,底面半径是16cm,高是30cm,将其铸造成底面半径是4cm,高是6cm的圆锥形钢坯,可以铸造多少个?
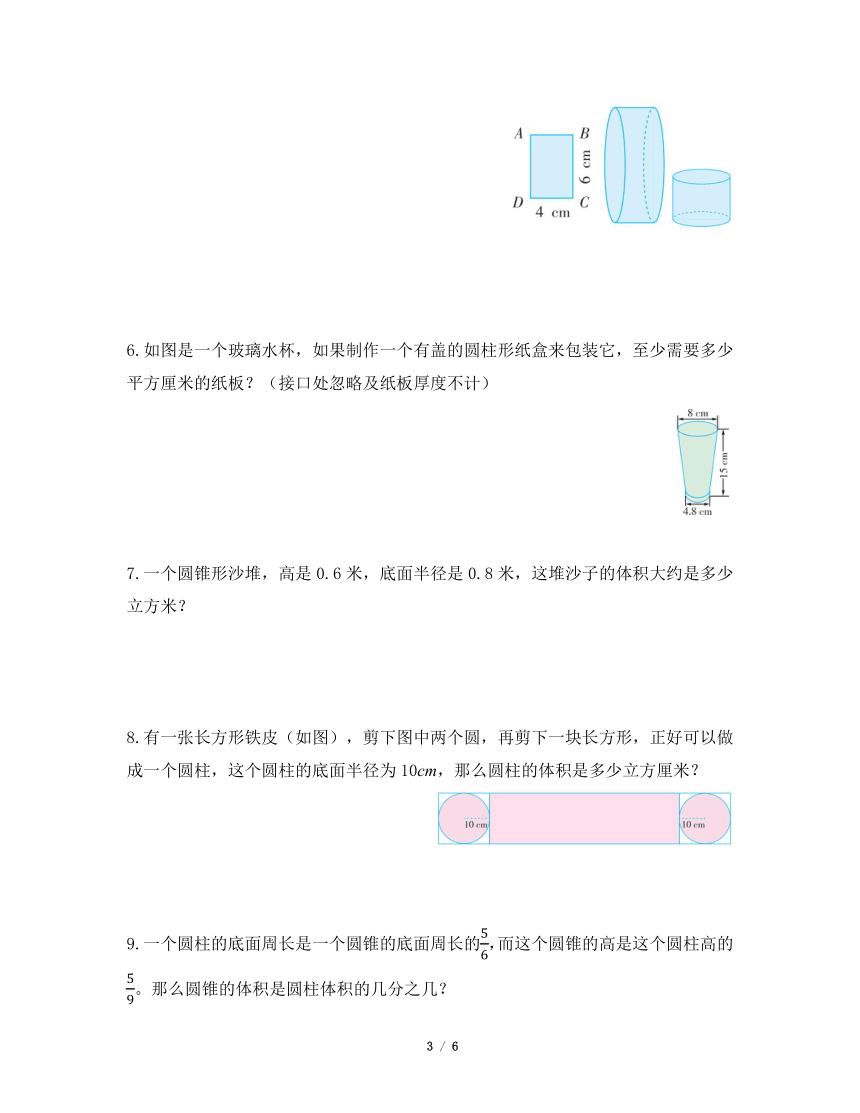
5.把长方形ABCD分别以AB边和AD边所在的直线为轴旋转,得到两个圆柱(如下图)。哪个圆柱的表面积更大?体积呢?
6.如图是一个玻璃水杯,如果制作一个有盖的圆柱形纸盒来包装它,至少需要多少平方厘米的纸板?(接口处忽略及纸板厚度不计)
7.一个圆锥形沙堆,高是0.6米,底面半径是0.8米,这堆沙子的体积大约是多少立方米?
8.有一张长方形铁皮(如图),剪下图中两个圆,再剪下一块长方形,正好可以做成一个圆柱,这个圆柱的底面半径为10cm,那么圆柱的体积是多少立方厘米?
9.一个圆柱的底面周长是一个圆锥的底面周长的,而这个圆锥的高是这个圆柱高的。那么圆锥的体积是圆柱体积的几分之几?
10.在一个圆柱形水桶里,把一段底面半径为6cm的圆柱形钢材浸没在水中,这时水面上升9cm且水没有溢出。把这段钢材竖着拉出水面8cm(钢材未完全离开水),水面下降4cm。求这段钢材的体积是多少立方厘米。
参考答案:
1.C C A B
2.(1)
(2)② ③ 62.8 (或① ④ 25.905)
(3)1413
3.10×10×10=1000(cm )
1000-3.14×(8÷2) ×10=497.6(cm )
1000-3.14×(5÷2) ×10×4=215(cm )
497.6-215=282.6(cm )
答:用正方体木块A削一个底面直径8cm、高10cm的圆柱剩下的木料比较多,多282.6cm 。
4.3.14×16 ×30÷(3.14×4 ×6×)=240(个)
答:可以铸造240个。
5.以AB边所在直线为轴旋转
表面积:
3.14×6 ×2+2×3.14×6×4=376.8(cm )
体积:3.14×6 ×4=452.16(cm )
以AD边所在直线为轴旋转
表面积:
3.14×4 ×2+2×3.14×4×6=251.2(cm )
体积:3.14×4 ×6=301.44(cm )
376.8>251.2 452.16>301.44
答:以AB边所在直线为轴旋转得到的圆柱的表面积和体积都更大。
6.3.14×(8÷2) ×2+3.14×8×15=477.28(cm )
答:至少需要477.28cm 的纸板。
7.3.14×0.8 ×0.6×÷4=0.10048(m )
答:这堆沙子的体积大约是0.10048m ,
8.3.14×10 ×(10×2)=6280(cm )
答:圆柱的体积是6280cm 。
9.设圆锥的底面半径是r,则圆柱的底面半径是r;圆锥的高是h,则圆柱的高是h。
圆锥的体积为πr h
圆柱的体积为π×(r) ×h=πr h=×(πr h)
答:圆锥的体积是圆柱体积的。
10.3.14×6 ×8÷4×9=2034.72(cm )
答:这段钢材的体积是2034.72cm 。
1 / 6
1.选一选。(将正确答案前的字母填在括号里)
(1)把一个圆柱的侧面展开,不可能得到下面的( )图形。
A. B. C.
(2)已知一个正方体的底面周长和一个圆柱的底面周长相等,它们的高也相等。它们的表面积相比,( )。
A.相等
B.正方体的表面积大于圆柱的表面积
C.正方体的表面积小于圆柱的表面积
(3)用一张长6厘米、宽2厘米的长方形纸卷成一个圆柱,按( )的方式卷,得到的圆柱体积最大。
A.以2厘米作为圆柱的高
B.以6厘米作为圆柱的高
C.无论哪种
(4)一个圆柱和一个圆锥的高和体积分别相等,那么圆柱的底面积是圆锥底面积的( )。
A.3倍 B. C.
2.认真想,仔细填。
(1)
图形 底面半径 底面直径 高 表面积 体积
圆柱 2 cm 5cm
10dm 8dm
圆锥 4.8m 10m ——
0.6m 1.2m ——
(2)要制作一个无盖圆柱形水桶,有以下四种型号的铁皮可供搭配选择。(铁皮不可切割)
① ② ③ ④
你选择的是( )号和( )号,用你选择的材料制作的水桶表面积是( )平方分米。
(3)张师傅要把一根底面直径10cm、高27cm的圆柱形木料削成一个最大的圆锥,削去的木料体积是( )立方厘米。
3.有两个棱长都是10cm的正方体木块A和B。用正方体木块A削一个底面直径8cm、高10cm的圆柱;用正方体木块B削4个底面直径5cm、高10cm的圆柱。剩下的木料哪个多,多多少?(请用计算过程说明理由)
4.一个圆柱形钢坯,底面半径是16cm,高是30cm,将其铸造成底面半径是4cm,高是6cm的圆锥形钢坯,可以铸造多少个?
5.把长方形ABCD分别以AB边和AD边所在的直线为轴旋转,得到两个圆柱(如下图)。哪个圆柱的表面积更大?体积呢?
6.如图是一个玻璃水杯,如果制作一个有盖的圆柱形纸盒来包装它,至少需要多少平方厘米的纸板?(接口处忽略及纸板厚度不计)
7.一个圆锥形沙堆,高是0.6米,底面半径是0.8米,这堆沙子的体积大约是多少立方米?
8.有一张长方形铁皮(如图),剪下图中两个圆,再剪下一块长方形,正好可以做成一个圆柱,这个圆柱的底面半径为10cm,那么圆柱的体积是多少立方厘米?
9.一个圆柱的底面周长是一个圆锥的底面周长的,而这个圆锥的高是这个圆柱高的。那么圆锥的体积是圆柱体积的几分之几?
10.在一个圆柱形水桶里,把一段底面半径为6cm的圆柱形钢材浸没在水中,这时水面上升9cm且水没有溢出。把这段钢材竖着拉出水面8cm(钢材未完全离开水),水面下降4cm。求这段钢材的体积是多少立方厘米。
参考答案:
1.C C A B
2.(1)
(2)② ③ 62.8 (或① ④ 25.905)
(3)1413
3.10×10×10=1000(cm )
1000-3.14×(8÷2) ×10=497.6(cm )
1000-3.14×(5÷2) ×10×4=215(cm )
497.6-215=282.6(cm )
答:用正方体木块A削一个底面直径8cm、高10cm的圆柱剩下的木料比较多,多282.6cm 。
4.3.14×16 ×30÷(3.14×4 ×6×)=240(个)
答:可以铸造240个。
5.以AB边所在直线为轴旋转
表面积:
3.14×6 ×2+2×3.14×6×4=376.8(cm )
体积:3.14×6 ×4=452.16(cm )
以AD边所在直线为轴旋转
表面积:
3.14×4 ×2+2×3.14×4×6=251.2(cm )
体积:3.14×4 ×6=301.44(cm )
376.8>251.2 452.16>301.44
答:以AB边所在直线为轴旋转得到的圆柱的表面积和体积都更大。
6.3.14×(8÷2) ×2+3.14×8×15=477.28(cm )
答:至少需要477.28cm 的纸板。
7.3.14×0.8 ×0.6×÷4=0.10048(m )
答:这堆沙子的体积大约是0.10048m ,
8.3.14×10 ×(10×2)=6280(cm )
答:圆柱的体积是6280cm 。
9.设圆锥的底面半径是r,则圆柱的底面半径是r;圆锥的高是h,则圆柱的高是h。
圆锥的体积为πr h
圆柱的体积为π×(r) ×h=πr h=×(πr h)
答:圆锥的体积是圆柱体积的。
10.3.14×6 ×8÷4×9=2034.72(cm )
答:这段钢材的体积是2034.72cm 。
1 / 6
