1.2 动量守恒定律 课件(共32页)
文档属性
| 名称 | 1.2 动量守恒定律 课件(共32页) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-29 21:51:13 | ||
图片预览







文档简介
(共32张PPT)
1.2 动量守恒定律
前面已经学习了动量定理,下面再来研究两个发生相互作用的物体所组成的物体系统,在不受外力的情况下,二者发生相互作用前后各自的动量发生什么变化,整个物体系统的动量又将如何?
1、静止站在光滑的冰面上,小孩推大人一把,他们各自往相反的方向运动,谁运动得更快一些?他们的总动量是多少?
现象思考
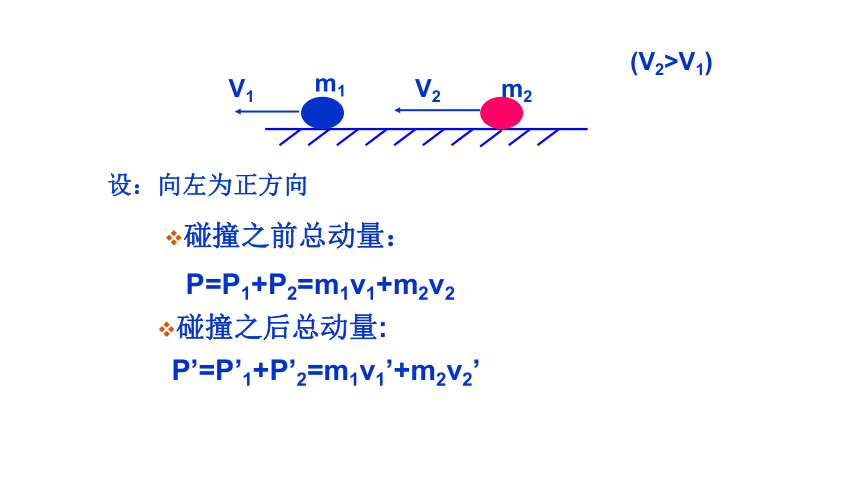
V1
V2
m1
m2
(V2>V1)
设:向左为正方向
碰撞之前总动量:
P=P1+P2=m1v1+m2v2
碰撞之后总动量:
P’=P’1+P’2=m1v1’+m2v2’
理论分析
1
1
1
1
1
v
m
v
m
t
F
-
=
2
2
2
2
2
v
m
v
m
t
F
-
=
∵ F1 = – F2
即
∴
故 p = p'
在碰撞过程中,
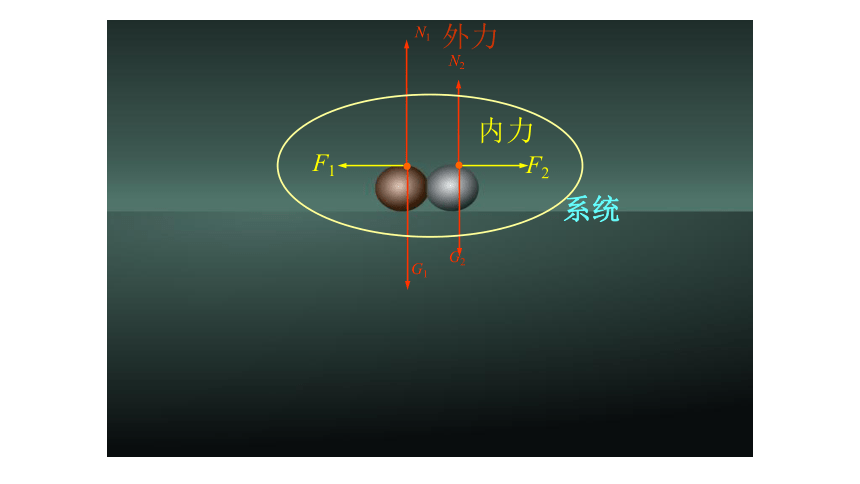
N1
G1
N2
G2
F1
F2
系统
内力
外力
3.内力:
一、基本概念
1.系统:
2.外力:
相互作用的物体组成系统。
系统以外物体对系统的作用力
系统内各物体间的相互作用力
结论:
1、系统的内力不改变系统的总动量
2、外力的冲量改变系统的动量
分析得到上述两球碰撞得出的结论的条件:
两球碰撞时除了它们相互间的作用力(系统的内力)外,还受到各自的重力和支持力 (外力)的作用,使它们彼此平衡。所以说m1和m2系统不受外力,或说它们所受的合外力为零。
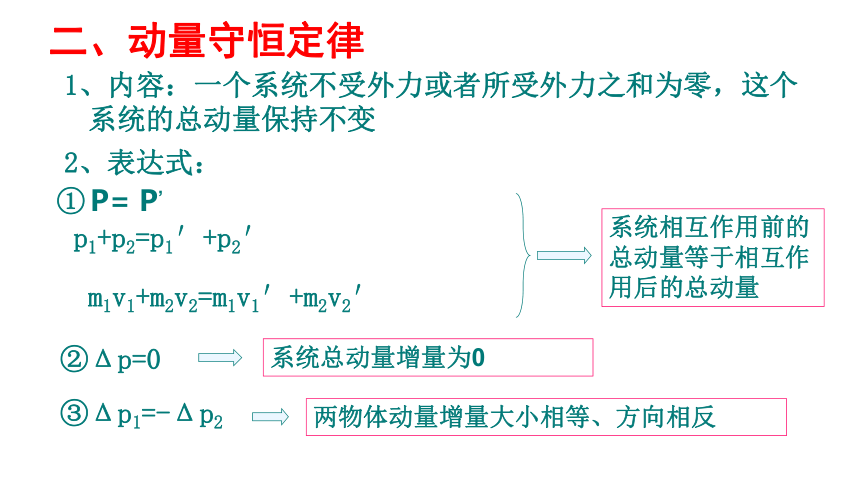
二、动量守恒定律
1、内容:一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变
2、表达式:
① P= P’
p1+p2=p1′+p2′
m1v1+m2v2=m1v1′+m2v2′
系统相互作用前的总动量等于相互作用后的总动量
②Δp=0
系统总动量增量为0
③Δp1=-Δp2
两物体动量增量大小相等、方向相反
3、守恒条件:
①不受外力或F合=0(严格条件)
(系统不受外力或所受外力的矢量和为零)
F内 》F外(近似条件)eg:爆炸、碰撞
(系统所受外力之和不为零,但系统内物体间相互作用的内力远大于外力,外力相对来说可以忽略不计)
③某方向上外力之和为零,在这个方向上动量守恒
(系统虽受外力,且不能忽略,但在某一方向上所受外力为0,则系统在这一方向上动量守恒)
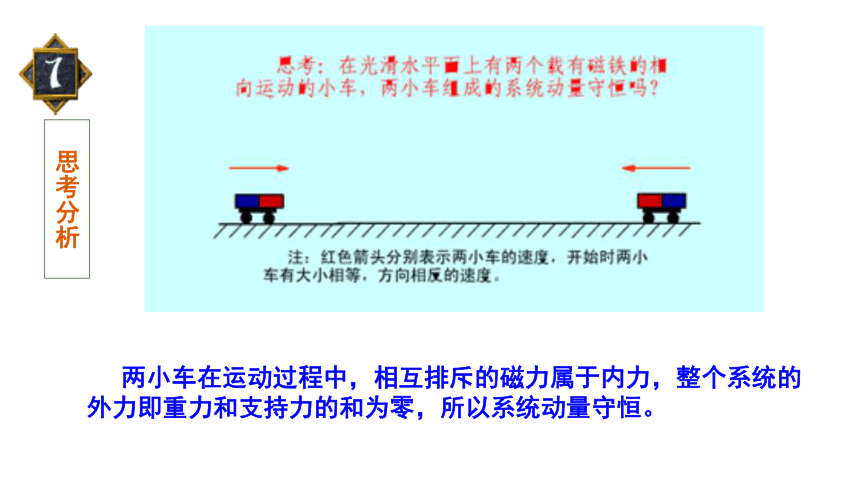
两小车在运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
思考分析
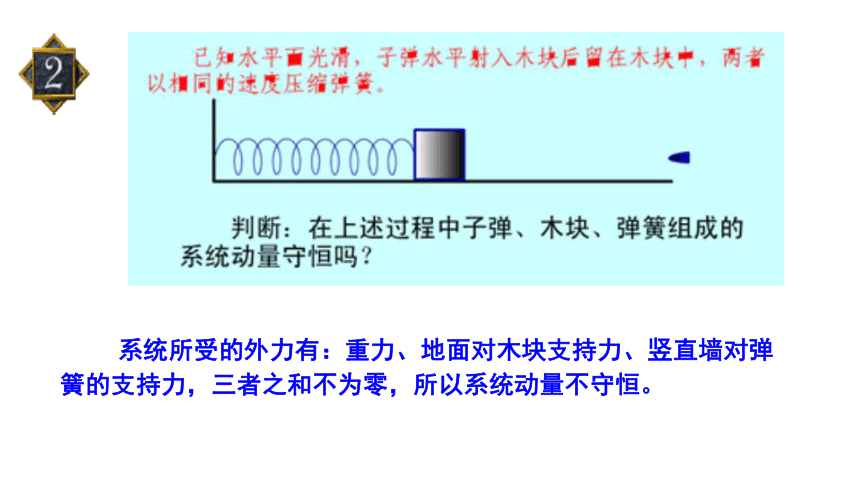
系统所受的外力有:重力、地面对木块支持力、竖直墙对弹簧的支持力,三者之和不为零,所以系统动量不守恒。
在光滑水平面的车上有一辆平板车,一个人站在车上用大锤敲打车的左端.在连续的敲打下,这辆车能持续地向右运动吗 说明理由.
台球的斜碰
货车的接合
正碰:一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心的连线在同一条直线上,碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰,也叫对心碰撞。
斜碰:一个运动的球与一个静止的球碰撞,如果碰撞之前球的运动速度与两球心的连线不在同一条直线上,碰撞之后两球的速度都会偏离原来两球心的连线。这种碰撞称为斜碰,也叫非对心碰撞。
①动量守恒定律
不仅适用于正碰,也适用于斜碰;
不仅适用于碰撞,也适用于任何形式的相互作用;
不仅适用于两个物体组成的系统,也适用于多个物体组成的系统。
4、适用范围:
②定律既适用于宏观物体的相互作用,也适用于微观粒子的相互作用,不管是低速还是高速问题均适用。
适用范围————普遍适用
5、动量守恒定律四性 :
①系统性:描述的对象是由两个以上的物体构成的系统 。
②矢量性 :系统内各物体相互作用前后均在同一直线上运动时,应首先选定正方向 。
③相对性 :表达式中各速度必须是相对同一参考系。一般以地面为参考系。
④同时性 :初态动量的速度都应该是互相作用前同一时刻的瞬时速度,末态动量中的速度都必须是相互作用后同一时刻的瞬时速度。
思考与讨论
木块B与水平桌面的接触是光滑的,子弹A沿水平方向射入木块后,留在木块内,将弹簧压缩到最短。现将子弹、木块和弹簧(质量不可忽略)合在一起作为研究对象(系统),此系统从子弹开始射入到弹簧压缩到最短的整个过程中,动量是否守恒 ?请说明理由。
B
A
N1
木块B与水平桌面的接触是光滑的,子弹A沿水平方向射入木块后,留要木块内,将弹簧压缩到最短,现将子弹、木块和弹簧(质量不可忽略)合在一起作为研究对象(系统),此系统从子弹开始射入到弹簧压缩到最短的整个过程中,动量是否守恒 ?请说明理由。
系统
N2
N4
N5
N6
外力
G
内力
N3
思考与讨论
假如将墙和弹簧去掉,问木块、子弹所组成的系统动量是否守恒 ?请说明理由。
思考与讨论
N1
N2
系统
内力
外力
思考与讨论
G
N3
思考与讨论
假如将墙去掉,而换作另一块木块,问两木块、弹簧和子弹组成的系统动量是否守恒 ?请说明理由。
系统
N1
N2
N4
N7
G
内力
N6
N3
N5
N8
外力
思考与讨论
分析与比较
例题1、在下列几种现象中,动量守恒的是( )
A、在静止的光滑水平面上,车上的人从车头走到车尾
B、水平放置的轻弹簧,一端固定于墙上,另一端与置于光滑水平面上的物体相连,开始时弹簧已有伸长,放手后物体在弹力的作用下运动
C、甲、乙两队进行拔河比赛,甲队获胜
D、汽车拉着拖车在平直的公路上做匀速直线运动,某时刻拖车突然脱钩离开汽车,由于司机没有发觉而保持汽车的驱动力不变,在拖车没有完全停下来的任何一段时间
AD
例题2、如图所示,气球与绳梯的质量为M,气球的绳梯上站着一个质量为m的人,原来整个系统处于静止状态,若空气阻力不计,当人沿绳梯向上爬时,对于整个系统来说动量是否守恒 为什么
人 气球系统合力为0,动量守恒
例题3、在光滑水平面上有甲、乙两小球,它们的质量分别为1kg和4kg,甲球以10m/s的速度向左运动,乙球以5m/s的速度向右运动,两球发生正碰后,乙球以1m/s的速度继续向右运动。求:
(1)甲球碰撞后的速度
(2)甲、乙两球各自受到的冲量
m1=1kg
m2=4kg
v1=10m/s
v2‘=1m/s
v2=5m/s
v1’=
+
解:甲乙两球组成的系统满足动量守恒条件,
设水平向右为正方向
根据动量守恒定律
m1v1+m2v2=m1v1’+m2v2’
矢量方程,注意代符号运算
甲球碰撞后速度大小为6m/s,方向水平向左
例题3、在光滑水平面上有甲、乙两小球,它们的质量分别为1kg和4kg,甲球以10m/s的速度向左运动,乙球以5m/s的速度向右运动,两球发生正碰后,乙球以1m/s的速度继续向右运动。求:
(1)甲球碰撞后的速度
(2)甲、乙两球各自受到的冲量
m1=1kg
m2=4kg
v1=10m/s
v2‘=1m/s
v2=5m/s
v1’=6m/s
+
(2)根据动量定理
甲球:I1 = m1v1’- m1v1 = [1×(-6)-1×10]N·s=-16N·s
乙球:I2 = m2v2’- m2v2 = [4×(-1)-4×(-5)]N·s=16N·s
4、写出动量守恒表达式,求解计算
系统确定
守恒条件确定
状态确定
参考系确定
正方向确定
6、应用动量守恒定律解题的步骤:
1、选取适当的研究对象(系统)
3、选定参考系,并选取正方向。确定初、末状态各物体的动量
2、进行受力分析,判断系统的动量是否守恒
(矢量性)
(相对性)
(同时性)
如图,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以v0/2的速率弹回,而B球以v0/3的速率向右运动,求A、B两球的质量之比
A
B
V0
2/9
关于爆炸,下列说法中正确的是 ( )
A、爆炸时由于物体所受到的合外力不为零,故动量一般认为不守恒
B、爆炸时,由于内力远大于外力,故认为动量守恒
C、爆炸时动能一定会损失
D、爆炸时动能增加,动量也增加
B
项目 动量守恒定律
内容 系统不受外力或所受外力的合力为零,这个系统的动量就保持不变。
公式
应用对象 物体系统
动量守恒 条件 研究的系统不受外力或合外力为零,或满足系统所受外力远小于系统内力。
特点 动量是矢量,式中动量的确定一般取地球为参照物。
小结
1.2 动量守恒定律
前面已经学习了动量定理,下面再来研究两个发生相互作用的物体所组成的物体系统,在不受外力的情况下,二者发生相互作用前后各自的动量发生什么变化,整个物体系统的动量又将如何?
1、静止站在光滑的冰面上,小孩推大人一把,他们各自往相反的方向运动,谁运动得更快一些?他们的总动量是多少?
现象思考
V1
V2
m1
m2
(V2>V1)
设:向左为正方向
碰撞之前总动量:
P=P1+P2=m1v1+m2v2
碰撞之后总动量:
P’=P’1+P’2=m1v1’+m2v2’
理论分析
1
1
1
1
1
v
m
v
m
t
F
-
=
2
2
2
2
2
v
m
v
m
t
F
-
=
∵ F1 = – F2
即
∴
故 p = p'
在碰撞过程中,
N1
G1
N2
G2
F1
F2
系统
内力
外力
3.内力:
一、基本概念
1.系统:
2.外力:
相互作用的物体组成系统。
系统以外物体对系统的作用力
系统内各物体间的相互作用力
结论:
1、系统的内力不改变系统的总动量
2、外力的冲量改变系统的动量
分析得到上述两球碰撞得出的结论的条件:
两球碰撞时除了它们相互间的作用力(系统的内力)外,还受到各自的重力和支持力 (外力)的作用,使它们彼此平衡。所以说m1和m2系统不受外力,或说它们所受的合外力为零。
二、动量守恒定律
1、内容:一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变
2、表达式:
① P= P’
p1+p2=p1′+p2′
m1v1+m2v2=m1v1′+m2v2′
系统相互作用前的总动量等于相互作用后的总动量
②Δp=0
系统总动量增量为0
③Δp1=-Δp2
两物体动量增量大小相等、方向相反
3、守恒条件:
①不受外力或F合=0(严格条件)
(系统不受外力或所受外力的矢量和为零)
F内 》F外(近似条件)eg:爆炸、碰撞
(系统所受外力之和不为零,但系统内物体间相互作用的内力远大于外力,外力相对来说可以忽略不计)
③某方向上外力之和为零,在这个方向上动量守恒
(系统虽受外力,且不能忽略,但在某一方向上所受外力为0,则系统在这一方向上动量守恒)
两小车在运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
思考分析
系统所受的外力有:重力、地面对木块支持力、竖直墙对弹簧的支持力,三者之和不为零,所以系统动量不守恒。
在光滑水平面的车上有一辆平板车,一个人站在车上用大锤敲打车的左端.在连续的敲打下,这辆车能持续地向右运动吗 说明理由.
台球的斜碰
货车的接合
正碰:一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心的连线在同一条直线上,碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰,也叫对心碰撞。
斜碰:一个运动的球与一个静止的球碰撞,如果碰撞之前球的运动速度与两球心的连线不在同一条直线上,碰撞之后两球的速度都会偏离原来两球心的连线。这种碰撞称为斜碰,也叫非对心碰撞。
①动量守恒定律
不仅适用于正碰,也适用于斜碰;
不仅适用于碰撞,也适用于任何形式的相互作用;
不仅适用于两个物体组成的系统,也适用于多个物体组成的系统。
4、适用范围:
②定律既适用于宏观物体的相互作用,也适用于微观粒子的相互作用,不管是低速还是高速问题均适用。
适用范围————普遍适用
5、动量守恒定律四性 :
①系统性:描述的对象是由两个以上的物体构成的系统 。
②矢量性 :系统内各物体相互作用前后均在同一直线上运动时,应首先选定正方向 。
③相对性 :表达式中各速度必须是相对同一参考系。一般以地面为参考系。
④同时性 :初态动量的速度都应该是互相作用前同一时刻的瞬时速度,末态动量中的速度都必须是相互作用后同一时刻的瞬时速度。
思考与讨论
木块B与水平桌面的接触是光滑的,子弹A沿水平方向射入木块后,留在木块内,将弹簧压缩到最短。现将子弹、木块和弹簧(质量不可忽略)合在一起作为研究对象(系统),此系统从子弹开始射入到弹簧压缩到最短的整个过程中,动量是否守恒 ?请说明理由。
B
A
N1
木块B与水平桌面的接触是光滑的,子弹A沿水平方向射入木块后,留要木块内,将弹簧压缩到最短,现将子弹、木块和弹簧(质量不可忽略)合在一起作为研究对象(系统),此系统从子弹开始射入到弹簧压缩到最短的整个过程中,动量是否守恒 ?请说明理由。
系统
N2
N4
N5
N6
外力
G
内力
N3
思考与讨论
假如将墙和弹簧去掉,问木块、子弹所组成的系统动量是否守恒 ?请说明理由。
思考与讨论
N1
N2
系统
内力
外力
思考与讨论
G
N3
思考与讨论
假如将墙去掉,而换作另一块木块,问两木块、弹簧和子弹组成的系统动量是否守恒 ?请说明理由。
系统
N1
N2
N4
N7
G
内力
N6
N3
N5
N8
外力
思考与讨论
分析与比较
例题1、在下列几种现象中,动量守恒的是( )
A、在静止的光滑水平面上,车上的人从车头走到车尾
B、水平放置的轻弹簧,一端固定于墙上,另一端与置于光滑水平面上的物体相连,开始时弹簧已有伸长,放手后物体在弹力的作用下运动
C、甲、乙两队进行拔河比赛,甲队获胜
D、汽车拉着拖车在平直的公路上做匀速直线运动,某时刻拖车突然脱钩离开汽车,由于司机没有发觉而保持汽车的驱动力不变,在拖车没有完全停下来的任何一段时间
AD
例题2、如图所示,气球与绳梯的质量为M,气球的绳梯上站着一个质量为m的人,原来整个系统处于静止状态,若空气阻力不计,当人沿绳梯向上爬时,对于整个系统来说动量是否守恒 为什么
人 气球系统合力为0,动量守恒
例题3、在光滑水平面上有甲、乙两小球,它们的质量分别为1kg和4kg,甲球以10m/s的速度向左运动,乙球以5m/s的速度向右运动,两球发生正碰后,乙球以1m/s的速度继续向右运动。求:
(1)甲球碰撞后的速度
(2)甲、乙两球各自受到的冲量
m1=1kg
m2=4kg
v1=10m/s
v2‘=1m/s
v2=5m/s
v1’=
+
解:甲乙两球组成的系统满足动量守恒条件,
设水平向右为正方向
根据动量守恒定律
m1v1+m2v2=m1v1’+m2v2’
矢量方程,注意代符号运算
甲球碰撞后速度大小为6m/s,方向水平向左
例题3、在光滑水平面上有甲、乙两小球,它们的质量分别为1kg和4kg,甲球以10m/s的速度向左运动,乙球以5m/s的速度向右运动,两球发生正碰后,乙球以1m/s的速度继续向右运动。求:
(1)甲球碰撞后的速度
(2)甲、乙两球各自受到的冲量
m1=1kg
m2=4kg
v1=10m/s
v2‘=1m/s
v2=5m/s
v1’=6m/s
+
(2)根据动量定理
甲球:I1 = m1v1’- m1v1 = [1×(-6)-1×10]N·s=-16N·s
乙球:I2 = m2v2’- m2v2 = [4×(-1)-4×(-5)]N·s=16N·s
4、写出动量守恒表达式,求解计算
系统确定
守恒条件确定
状态确定
参考系确定
正方向确定
6、应用动量守恒定律解题的步骤:
1、选取适当的研究对象(系统)
3、选定参考系,并选取正方向。确定初、末状态各物体的动量
2、进行受力分析,判断系统的动量是否守恒
(矢量性)
(相对性)
(同时性)
如图,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以v0/2的速率弹回,而B球以v0/3的速率向右运动,求A、B两球的质量之比
A
B
V0
2/9
关于爆炸,下列说法中正确的是 ( )
A、爆炸时由于物体所受到的合外力不为零,故动量一般认为不守恒
B、爆炸时,由于内力远大于外力,故认为动量守恒
C、爆炸时动能一定会损失
D、爆炸时动能增加,动量也增加
B
项目 动量守恒定律
内容 系统不受外力或所受外力的合力为零,这个系统的动量就保持不变。
公式
应用对象 物体系统
动量守恒 条件 研究的系统不受外力或合外力为零,或满足系统所受外力远小于系统内力。
特点 动量是矢量,式中动量的确定一般取地球为参照物。
小结
