2013数学总复习第三轮能力训练
图片预览


文档简介
能力训练(1)
1.计算:
2.先化简,再请你用喜爱的数代入求值
3.如图,M为双曲线y=上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.则AD·BC的值为 .
4.如图,在平行四边形ABCD中,AC = 4,BD = 6,P是
BD上的任一点,过P作EF∥AC,与平行四边形的两
条边分别交于点E,F.设BP=x,EF=y,则能大致反
映y与x之间关系的图象为( )
A B C D
5.如图,是反比例函数和()在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若,则的值是( )
A.1 B.2 C.4 D.8
6.如图,在平行四边形ABCD中,E是BC的中点,且∠AEC=∠DCE,
则下列结论不正确的是( )
A.S△AFD=2S△EFB B.BF=DF
C.四边形AECD是等腰梯形 D.∠AEB=∠ADC
7.已知如图,△ABC和△DCE都是等边三角形,若△ABC的边长为1,则△BAE的面积是 .
四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是 .
……
如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
8.如图,,过上到点的距离分别为的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为.
则第一个黑色梯形的面积 ;观察图中的规律,
第n(n为正整数)个黑色梯形的面积 .
9.有3张背面相同的纸牌A,B,C,其正面分别画有三个不同的几何图形(如图).将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.
(1)求出两次摸牌的所有等可能结果(用树状图或列表法求解,纸牌可用A,B,C表示);
(2)求摸出两张牌面图形都是中心对称图形的纸牌的概率.
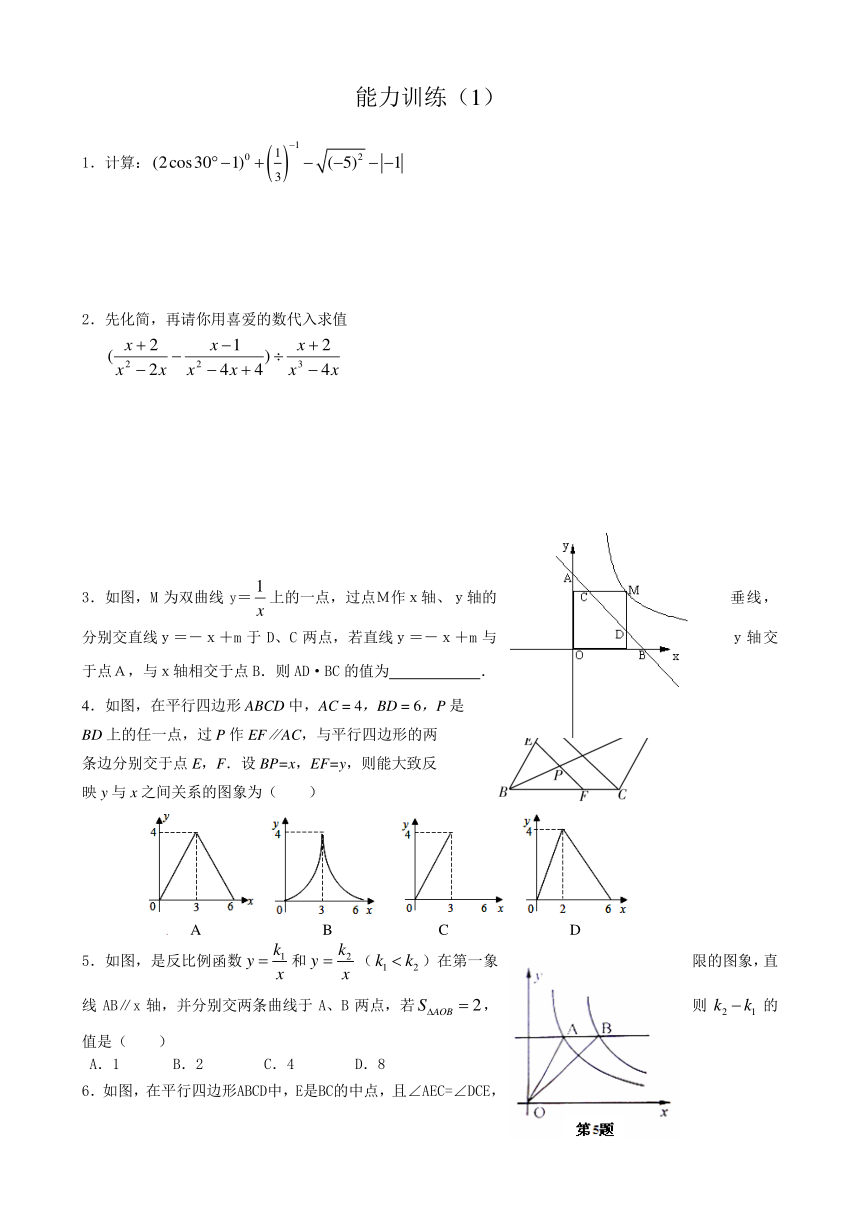
10. 已知:如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证: AC是⊙O的切线;
(2) 如果BC=9, AC=12,,求⊙O的半径r.
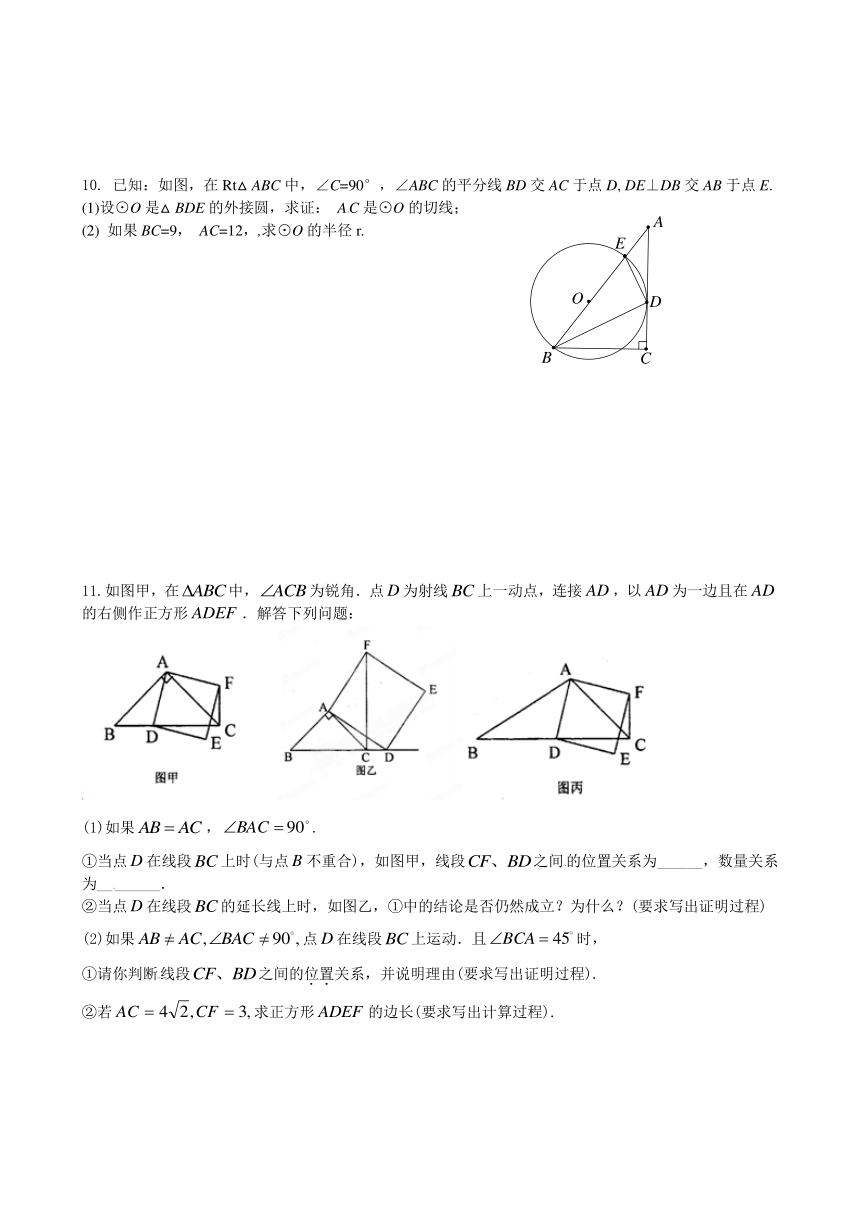
11.如图甲,在中,为锐角.点为射线上一动点,连接,以为一边且在的右侧作正方形.解答下列问题:
(1)如果,.
①当点在线段上时(与点不重合),如图甲,线段之间的位置关系为______,数量关系为________.
②当点在线段的延长线上时,如图乙,①中的结论是否仍然成立?为什么?(要求写出证明过程)
(2)如果点在线段上运动.且时,
①请你判断线段之间的位置关系,并说明理由(要求写出证明过程).
②若求正方形的边长(要求写出计算过程).
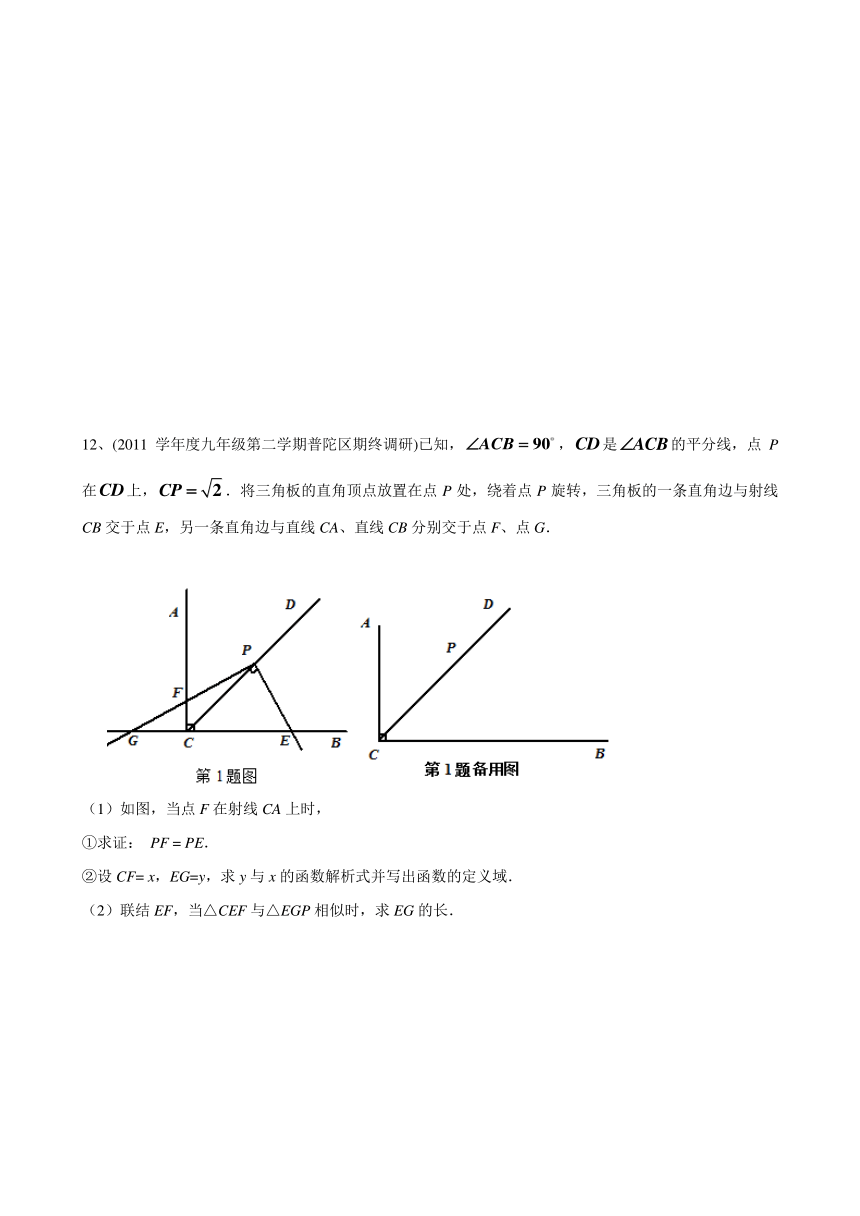
12、(2011学年度九年级第二学期普陀区期终调研)已知,,是的平分线,点P在上,.将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
(1)如图,当点F在射线CA上时,
①求证: PF = PE.
②设CF= x,EG=y,求y与x的函数解析式并写出函数的定义域.
(2)联结EF,当△CEF与△EGP相似时,求EG的长.
13.如图,将边长为a的正方形OABC绕顶点O按顺时针方向旋转角α(0°<α<45°),得到正方形OA1B1C1.设边B1C1与OC的延长线交于点M,边B1A1与OB交于点N,
边B1A1与OA的延长线交于点E,连接MN.
(1)求证:△OC1M≌△OA1E;
(2)试说明:△OMN的边MN上的高为定值;
(3)△MNB1的周长p是否发生变化?若发生变化,试说明理由;若不发生变化,
请给予证明,并求出p的值.
14.在图形的全等变换中,有旋转变换,翻折(轴对称)变换和平移变换.一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.
(1)第一小组的同学发现,在如图1-1的矩形ABCD中,AC、BD相交于点O,Rt△ADC可以由Rt△ABC经过一种变换得到,请你写出这种变换的过程 .
(2)第二小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图2-1);再沿GC折叠,使点B落在EF上的点B'处(如图2-2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.
(3)第三小组的同学,在一个矩形纸片上按照图3-1的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图3-2.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15,请你帮助该小组求出a可能的最大整数值.
(4)探究活动结束后,老师给大家留下了一道探究题:
如图4-1,已知AA'=BB'=CC'=2,∠AOB'=∠BOC'=∠COA'=60°,
请利用图形变换探究S△AOB'+S△BOC'+S△COA'与的大小关系.
基础题训练(1)
1. 据萧山区旅游局统计,2012年春节约有359525人来萧旅游, 将这个旅游人数 (保留三个有效数字)用科学计数法表示为 ( )
A.3.59× B.3.60× C.3.5 × D.3.6 ×
2.下列计算正确的是 ( )
A. B.
C. D.
3.化简的结果是 ( )
A. -x-y B. y-x C. x-y D .x+y
4.小明用一个半径为5,面积为15的扇形纸片,制作成一个圆锥的侧面(接缝处不重叠),那么这个圆锥的底面半径为 ( )
A.3 B.4 C.5 D.15
5. 已知下列命题:①若,则。 ②垂直于弦的直径平分弦。 ③平行四边形的对角线互相平分。 ④反比例函数y=,当k>0时,y随x的增大而减少。⑤在同圆或等圆中,等弧所对的圆周角相等。 其中原命题与逆命题均为真命题的是( ) A.①② B. ③④ C.③⑤ D.②④
6.如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四边形OABC绕点O进行3次旋转变换后形成的.测得AB=BC,OA=OC,∠ABC=40°,则∠OAB的度数是 ( )
A.117° B.116 ° C.115° D.137.5°
7.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,4:10:25 ,则DE:EC= ( )
A.2:3 B. 2:5 C. 3:5 D.3:2
8.抛物线y=x 2-x-与直线y=x-2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为( ).
A. B. C. D.
9.计算: 。
10.我们知道多项式可分解成(x-1)(x-2),所以方程=0有两根。已知多项式有一个因式是x+2,则k= 。
11.若关于x的不等式 的正整数解只有4个,则m的取值范围是 。
12.如图,直三棱柱的侧棱长和底面各边长均为,其主视图是边长为的正方形,则此直三棱柱左视图的面积为 。
13. P(x,y)位于第二象限,并且y,x,y为整数,写出所有符合上述条件的点P的坐标: 。
14. 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线。如上图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3),AB为半圆直径,半圆圆心M(1,0),半径为2,则“蛋圆”的抛物线部分的解析式为__________________。经过点C的“蛋圆”的切线的解析式为__________________。
15. 如图,A,B,C,D四张卡片上分别写有四个实数,从中两张卡片。
(1)请列举出所有可能的结果(用字母A,B,C,D表示);
(2)求取到的两个数都是无理数的概率。
A B C D
基础题训练(2)
1、下列各数中,相反数最大的是( )A.-1 B.0 C.1 D.-
2、我国云南大部分地区滴雨未降,正在经历严峻的干旱形势,云南省气象台为此发布全省干旱“红色预警”,干旱一周导致损失20亿。 截至到六月份,云南全省作物受旱面积1755万亩,因旱饮水困难的有385万人.其中受灾人数用科学记数法表示(保留两个有效数字)正确的是( )
A.0.385×107 B. C. D.
3、视力表对我们来说并不陌生.如图是视力表的一部分,五个不同
方向的“E”之间存在的变换有( )
A.平移、旋转 B.旋转、相似 、平移
C.轴对称、平移、相似 D.相似、平移
4、两个大小不同的球在水平面上靠在一起,组成如图所示的几何
体,则该几何体的左视图是( )
(A)两个外离的圆 (B)两个外切的圆(C)两个相交的圆 (D)两个内切的圆
5、有一个圆形人工湖如图所示,弦是湖上的一座桥,已知桥长100m,测得圆周角,则这个人工湖的直径为( ).
A. B. C. D.
6、在不大于100的自然数中,既不是完全平方数(平方根是整数)也不是完全立方数(立方根是整数)的数的概率有( )
A. B. C. D.
7、如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有( )
A.1个 B.2个 C.3个 D.4个
8、已知:如图,三个半圆彼此相外切,它们的圆心都在x轴的正半轴上并与直线y=x相切,设半圆C1、半圆C2、半圆C3…的半径分别是r1、r2、r3….,则当r1=1时,则=( )
A、 B、 C、 D、
9、-(-4)-1+-2cos30°=_______
10、数据,4,2,5,3的平均数为,且和是方程的两个根,则=
11、已知△ABC中,AB=AC=5,BC=8.⊙O经过B、C两点,且AO=4,则⊙O的半径长是___________
12、先化简再求值:,并从不等式<<tan解中选一个你喜欢的数代入,求原分式的值.
13、某市国际动漫节开幕前,星空动漫公司预测某种动漫玩具能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,动漫公司又用69000元购进第二批这种玩具,所购数量是笫一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司两次共购进这种玩具多少套?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低20%,那么每套售价至少是多少元?
基础题训练(3)
1.-3的相反数是【 】
A.3 B.-3 C. D.
2.中国人民银行决定,从2012年2月24日起,下调存款类金融机构人民币存款准备金率0.5个百分点.本次下调后,央行一次性释放约4 000亿元人民币的资金.请把4 000亿元用科学记数法表示应为【 】
A.元 B.元 C.元 D. 元
3.下列图形中,是中心对称图形而不是轴对称图形的是【 】
A.等边三角形 B.矩形 C.菱形 D.平行四边形
4.下列运算正确的是【 】
A. B. C. D.
职务
经理
副经理
职员
人数
1
2
12
月工资(元)
5 000
2 000
800
5.某个公司有15名工作人员,他们的月工资情况如下表.则该公司所有工作人员的月工资的平均数、中位数和众数分别是【 】
A.520,2 000,2 000 B.2 600, 800,800
C.1 240,2 000,800 D.1 240,800,800
6.如图,AB∥CD,点E在AB上,点F在CD上,且,
,则的度数是【 】
A.25° B.35° C.45° D.55 °
7.一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,求这张卡片与口袋外的两张卡片上的数能构成三角形的概率是【 】
A. B. C. D.1
8.如图,在Rt△ABC中,,,AC=2,
D是AB边上一个动点(不与点A、B重合),E是BC边上
一点,且.设AD=x, BE=y,则下列图象中,
能表示y与x的函数关系的图象大致是【 】
9.分解因式: .
10.如图,用测角仪测得校园的旗杆顶点A的仰角,仪器高米,测角仪底部中心位置D到旗杆根部B的距离米,则旗杆的高是 米
11.计算:.
12.如图,C是⊙O的直径AB延长线上一点,点D在⊙O上,且∠A=30°,∠BDC =.
(1)求证:CD是⊙O的切线;
(2)若OF∥AD分别交BD、CD于E、F,BD =2,求OE及CF的长.
基础题训练(4)
1.的相反数是【 】
A. B. C. D.
2. 2012年第七届原创新春祝福短信微博大赛作品充满了对龙年浓浓的祝福, 主办方共收
到原创祝福短信作品41 430条,将41 430用科学记数法表示应为【 】
A.41.43 ( 103 B.4.143 ( 104 C.0.4143 ( 105 D.4.143( 105
3. 如图, 点A、B、C在⊙上, 若(C=40(, 则(AOB的度数为【 】
A.20( B.40( C.80( D.100(
4.掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面 的点数为偶数的概率为【 】
A. B. C. D.
5.将代数式化为的形式, 正确的是【 】
A. B. C. D.
6.如图,在△ABC中,(C=90(, 点D在CB上,DE(AB于E,若DE=2, CA=4,则 的值为【 】
A. B. C. D.
7. 北京市环保检测中心网站公布的2012年3月31日的PM2.5研究性检测部分数据如下表:
时间
0:00
4:00
8:00
12:00
16:00
20:00
PM2.5(mg/m3)
0.027
0.035
0.032
0.014
0.016
0.032
则该日这6个时刻的PM2.5的众数和中位数分别是【 】
A. 0.032, 0.0295 B. 0.026, 0.0295 C. 0.026, 0.032 D. 0.032, 0.027
8.下列图形中,能通过折叠围成一个三棱柱的是【 】
A B C D
9.函数y=的自变量的取值范围是 .
10.分解因式:x3 - 4x= .
11. 右图是某超市一层到二层滚梯示意图.其中AB、CD分别
表示超市一层、二层滚梯口处地面的水平线, ∠ABC=150°,
BC的长约为12米,则乘滚梯从点B到点C上升的高度h
约为 米.
12. 在平面直角坐标系xOy中, 正方形A1B1C1O、
A2B2C2B1、A3B3C3B2, …,按右图所示的方
式放置. 点A1、A2、A3, …和 B1、B2、B3, …
分别在直线y=kx+b和x轴上. 已知C1(1, -1),
C 2(), 则点A3的坐标是 ;
点An的坐标是 .
三、解答题
13.计算:.14.解不等式组:
15. 如图,AC//FE, 点F、C在BD上,AC=DF, BC=EF.
求证:AB=DE.
16.如图,△ABC内接于⊙O, AD是⊙O直径, E是CB延长线上一点, 且(BAE=(C.
(1)求证:直线AE是⊙O的切线;
(2)若EB=AB , , AE=24,求EB的长及⊙O的半径.
能力训练(2)
1.(2012年江西南昌十五校联考)将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1.在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.2
2.(2012年上海市黄浦二模)如图3,在Rt中,,点在上,且,,若将绕点顺时针旋转得到Rt,且落在的延长线上,联结交的延长线于点,则= .
3.(河南省信阳市二中).如图,在等腰梯形中,,=4=,=45°.直角三角板含45°角的顶点在边上移动,一直角边始终经过点,斜边与交于点.若为等腰三角形,则的长等于
4.(2012年,辽宁省营口市)直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为,则的值是___。
5.(2012年广东模拟)如图,将边长为的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交于点M、N,DFAB,垂足为D,AD=2.设△DBE的面积为,则重叠部分的面积为 .(用含S的式子表示)
6.甲学校到丙学校要经过乙学校. 从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了B1线路的概率是多少?
7.如图,在△ABC中,AB=AC,以AB边的中点O为圆心,线段OA的长为半径作圆,分别交BC、AC边于点D、E,DF⊥AC于点F,延长FD交AB延长线于点G .
(1)求证:FD是⊙O的切线.
(2)若BC=AD=4,求的值.
8.阅读下列材料:
问题:如图1,P为正方形ABCD内一点,且PA∶PB∶PC=1∶2∶3,求∠APB的度数.
小娜同学的想法是:不妨设PA=1, PB=2,PC=3,设法把PA、PB、PC相对集中,于是他将△BCP绕点B顺时针旋转90°得到△BAE(如图2),然后连结PE,问题得以解决.
请你回答:图2中∠APB的度数为 .
请你参考小娜同学的思路,解决下列问题:
如图3,P是等边三角形ABC内一点,已知∠APB=115°,∠BPC=125°.
(1)在图3中画出并指明以PA、PB、PC的长度为三边长的一个三角形(保留画图痕迹);
(2)求出以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于 .
图1 图2 图3
9.(2012山东省德州四模)如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC = 4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
⑴当x为何值时,△APD是等腰三角形?
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
10. 有两张完全重合的矩形纸片,小亮将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连结BD、MF,此时他测得BD=8cm,∠ADB=30°.
(1)在图1中,请你判断直线FM和BD是否垂直?并证明你的结论;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少.
11.24.已知:如图,D为线段AB上一点(不与点A、B重合),CD⊥AB,且CD=AB,AE⊥AB,BF⊥AB,且AE=BD,BF=AD.
(1)如图1,当点D恰是AB的中点时,请你猜想并证明∠ACE与∠BCF的数量关系;
(2)如图2,当点D不是AB的中点时,你在(1)中所得的结论是否发生变化,写出你的猜想并证明;
(3)若∠ACB=,直接写出∠ECF的度数(用含的式子表示).
图1 图2
12.如图,将矩形OABC置于平面直角坐标系xOy中,A(,0),C(0,2).
(1) 抛物线经过点B、C,求该抛物线的解析式;
(2)将矩形OABC绕原点顺时针旋转一个角度(0°<<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标;
(3)如图(2),将矩形OABC绕原点顺时针旋转一个角度(0°<<180°),将得到矩形OA’B’C’,设A’C’的中点为点E,联结CE,当 °时,线段CE的长度最大,最大值为 .
13.如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=,直线y=经过点C,交y轴于点G。
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=上且经过点C、D的抛物线的
解析式;
(3)将(2)中的抛物线沿直线y=平移,平移
后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说明
理由。
如图,△ABC, △DCE,△GEF都是正三角形,且B,C,E,F在同一直线上,A,D,G也在同一直线上, 设△ABC, △DCE,△GEF的面积分别为.当时, _________
18.有依次排列的3个数:2,8,7.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2,6,8,-1,7,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:2,4,6,2,8,-9,-1,8,7;继续依次操作下去……,那么从数串2,8,7开始操作第100次后所产生的那个新数串的所有数之和是 .
8.已知:如图,P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,BC∥OP交⊙O于点C.
(1)判断直线PC与⊙O的位置关系,并证明你的结论;
(2)若BC=2,,求PC的长及点C到PA的距离.
1.计算:
2.先化简,再请你用喜爱的数代入求值
3.如图,M为双曲线y=上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.则AD·BC的值为 .
4.如图,在平行四边形ABCD中,AC = 4,BD = 6,P是
BD上的任一点,过P作EF∥AC,与平行四边形的两
条边分别交于点E,F.设BP=x,EF=y,则能大致反
映y与x之间关系的图象为( )
A B C D
5.如图,是反比例函数和()在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若,则的值是( )
A.1 B.2 C.4 D.8
6.如图,在平行四边形ABCD中,E是BC的中点,且∠AEC=∠DCE,
则下列结论不正确的是( )
A.S△AFD=2S△EFB B.BF=DF
C.四边形AECD是等腰梯形 D.∠AEB=∠ADC
7.已知如图,△ABC和△DCE都是等边三角形,若△ABC的边长为1,则△BAE的面积是 .
四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是 .
……
如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
8.如图,,过上到点的距离分别为的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为.
则第一个黑色梯形的面积 ;观察图中的规律,
第n(n为正整数)个黑色梯形的面积 .
9.有3张背面相同的纸牌A,B,C,其正面分别画有三个不同的几何图形(如图).将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.
(1)求出两次摸牌的所有等可能结果(用树状图或列表法求解,纸牌可用A,B,C表示);
(2)求摸出两张牌面图形都是中心对称图形的纸牌的概率.
10. 已知:如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证: AC是⊙O的切线;
(2) 如果BC=9, AC=12,,求⊙O的半径r.
11.如图甲,在中,为锐角.点为射线上一动点,连接,以为一边且在的右侧作正方形.解答下列问题:
(1)如果,.
①当点在线段上时(与点不重合),如图甲,线段之间的位置关系为______,数量关系为________.
②当点在线段的延长线上时,如图乙,①中的结论是否仍然成立?为什么?(要求写出证明过程)
(2)如果点在线段上运动.且时,
①请你判断线段之间的位置关系,并说明理由(要求写出证明过程).
②若求正方形的边长(要求写出计算过程).
12、(2011学年度九年级第二学期普陀区期终调研)已知,,是的平分线,点P在上,.将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
(1)如图,当点F在射线CA上时,
①求证: PF = PE.
②设CF= x,EG=y,求y与x的函数解析式并写出函数的定义域.
(2)联结EF,当△CEF与△EGP相似时,求EG的长.
13.如图,将边长为a的正方形OABC绕顶点O按顺时针方向旋转角α(0°<α<45°),得到正方形OA1B1C1.设边B1C1与OC的延长线交于点M,边B1A1与OB交于点N,
边B1A1与OA的延长线交于点E,连接MN.
(1)求证:△OC1M≌△OA1E;
(2)试说明:△OMN的边MN上的高为定值;
(3)△MNB1的周长p是否发生变化?若发生变化,试说明理由;若不发生变化,
请给予证明,并求出p的值.
14.在图形的全等变换中,有旋转变换,翻折(轴对称)变换和平移变换.一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.
(1)第一小组的同学发现,在如图1-1的矩形ABCD中,AC、BD相交于点O,Rt△ADC可以由Rt△ABC经过一种变换得到,请你写出这种变换的过程 .
(2)第二小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图2-1);再沿GC折叠,使点B落在EF上的点B'处(如图2-2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.
(3)第三小组的同学,在一个矩形纸片上按照图3-1的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图3-2.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15,请你帮助该小组求出a可能的最大整数值.
(4)探究活动结束后,老师给大家留下了一道探究题:
如图4-1,已知AA'=BB'=CC'=2,∠AOB'=∠BOC'=∠COA'=60°,
请利用图形变换探究S△AOB'+S△BOC'+S△COA'与的大小关系.
基础题训练(1)
1. 据萧山区旅游局统计,2012年春节约有359525人来萧旅游, 将这个旅游人数 (保留三个有效数字)用科学计数法表示为 ( )
A.3.59× B.3.60× C.3.5 × D.3.6 ×
2.下列计算正确的是 ( )
A. B.
C. D.
3.化简的结果是 ( )
A. -x-y B. y-x C. x-y D .x+y
4.小明用一个半径为5,面积为15的扇形纸片,制作成一个圆锥的侧面(接缝处不重叠),那么这个圆锥的底面半径为 ( )
A.3 B.4 C.5 D.15
5. 已知下列命题:①若,则。 ②垂直于弦的直径平分弦。 ③平行四边形的对角线互相平分。 ④反比例函数y=,当k>0时,y随x的增大而减少。⑤在同圆或等圆中,等弧所对的圆周角相等。 其中原命题与逆命题均为真命题的是( ) A.①② B. ③④ C.③⑤ D.②④
6.如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四边形OABC绕点O进行3次旋转变换后形成的.测得AB=BC,OA=OC,∠ABC=40°,则∠OAB的度数是 ( )
A.117° B.116 ° C.115° D.137.5°
7.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,4:10:25 ,则DE:EC= ( )
A.2:3 B. 2:5 C. 3:5 D.3:2
8.抛物线y=x 2-x-与直线y=x-2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为( ).
A. B. C. D.
9.计算: 。
10.我们知道多项式可分解成(x-1)(x-2),所以方程=0有两根。已知多项式有一个因式是x+2,则k= 。
11.若关于x的不等式 的正整数解只有4个,则m的取值范围是 。
12.如图,直三棱柱的侧棱长和底面各边长均为,其主视图是边长为的正方形,则此直三棱柱左视图的面积为 。
13. P(x,y)位于第二象限,并且y,x,y为整数,写出所有符合上述条件的点P的坐标: 。
14. 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线。如上图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3),AB为半圆直径,半圆圆心M(1,0),半径为2,则“蛋圆”的抛物线部分的解析式为__________________。经过点C的“蛋圆”的切线的解析式为__________________。
15. 如图,A,B,C,D四张卡片上分别写有四个实数,从中两张卡片。
(1)请列举出所有可能的结果(用字母A,B,C,D表示);
(2)求取到的两个数都是无理数的概率。
A B C D
基础题训练(2)
1、下列各数中,相反数最大的是( )A.-1 B.0 C.1 D.-
2、我国云南大部分地区滴雨未降,正在经历严峻的干旱形势,云南省气象台为此发布全省干旱“红色预警”,干旱一周导致损失20亿。 截至到六月份,云南全省作物受旱面积1755万亩,因旱饮水困难的有385万人.其中受灾人数用科学记数法表示(保留两个有效数字)正确的是( )
A.0.385×107 B. C. D.
3、视力表对我们来说并不陌生.如图是视力表的一部分,五个不同
方向的“E”之间存在的变换有( )
A.平移、旋转 B.旋转、相似 、平移
C.轴对称、平移、相似 D.相似、平移
4、两个大小不同的球在水平面上靠在一起,组成如图所示的几何
体,则该几何体的左视图是( )
(A)两个外离的圆 (B)两个外切的圆(C)两个相交的圆 (D)两个内切的圆
5、有一个圆形人工湖如图所示,弦是湖上的一座桥,已知桥长100m,测得圆周角,则这个人工湖的直径为( ).
A. B. C. D.
6、在不大于100的自然数中,既不是完全平方数(平方根是整数)也不是完全立方数(立方根是整数)的数的概率有( )
A. B. C. D.
7、如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有( )
A.1个 B.2个 C.3个 D.4个
8、已知:如图,三个半圆彼此相外切,它们的圆心都在x轴的正半轴上并与直线y=x相切,设半圆C1、半圆C2、半圆C3…的半径分别是r1、r2、r3….,则当r1=1时,则=( )
A、 B、 C、 D、
9、-(-4)-1+-2cos30°=_______
10、数据,4,2,5,3的平均数为,且和是方程的两个根,则=
11、已知△ABC中,AB=AC=5,BC=8.⊙O经过B、C两点,且AO=4,则⊙O的半径长是___________
12、先化简再求值:,并从不等式<<tan解中选一个你喜欢的数代入,求原分式的值.
13、某市国际动漫节开幕前,星空动漫公司预测某种动漫玩具能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,动漫公司又用69000元购进第二批这种玩具,所购数量是笫一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司两次共购进这种玩具多少套?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低20%,那么每套售价至少是多少元?
基础题训练(3)
1.-3的相反数是【 】
A.3 B.-3 C. D.
2.中国人民银行决定,从2012年2月24日起,下调存款类金融机构人民币存款准备金率0.5个百分点.本次下调后,央行一次性释放约4 000亿元人民币的资金.请把4 000亿元用科学记数法表示应为【 】
A.元 B.元 C.元 D. 元
3.下列图形中,是中心对称图形而不是轴对称图形的是【 】
A.等边三角形 B.矩形 C.菱形 D.平行四边形
4.下列运算正确的是【 】
A. B. C. D.
职务
经理
副经理
职员
人数
1
2
12
月工资(元)
5 000
2 000
800
5.某个公司有15名工作人员,他们的月工资情况如下表.则该公司所有工作人员的月工资的平均数、中位数和众数分别是【 】
A.520,2 000,2 000 B.2 600, 800,800
C.1 240,2 000,800 D.1 240,800,800
6.如图,AB∥CD,点E在AB上,点F在CD上,且,
,则的度数是【 】
A.25° B.35° C.45° D.55 °
7.一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,求这张卡片与口袋外的两张卡片上的数能构成三角形的概率是【 】
A. B. C. D.1
8.如图,在Rt△ABC中,,,AC=2,
D是AB边上一个动点(不与点A、B重合),E是BC边上
一点,且.设AD=x, BE=y,则下列图象中,
能表示y与x的函数关系的图象大致是【 】
9.分解因式: .
10.如图,用测角仪测得校园的旗杆顶点A的仰角,仪器高米,测角仪底部中心位置D到旗杆根部B的距离米,则旗杆的高是 米
11.计算:.
12.如图,C是⊙O的直径AB延长线上一点,点D在⊙O上,且∠A=30°,∠BDC =.
(1)求证:CD是⊙O的切线;
(2)若OF∥AD分别交BD、CD于E、F,BD =2,求OE及CF的长.
基础题训练(4)
1.的相反数是【 】
A. B. C. D.
2. 2012年第七届原创新春祝福短信微博大赛作品充满了对龙年浓浓的祝福, 主办方共收
到原创祝福短信作品41 430条,将41 430用科学记数法表示应为【 】
A.41.43 ( 103 B.4.143 ( 104 C.0.4143 ( 105 D.4.143( 105
3. 如图, 点A、B、C在⊙上, 若(C=40(, 则(AOB的度数为【 】
A.20( B.40( C.80( D.100(
4.掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面 的点数为偶数的概率为【 】
A. B. C. D.
5.将代数式化为的形式, 正确的是【 】
A. B. C. D.
6.如图,在△ABC中,(C=90(, 点D在CB上,DE(AB于E,若DE=2, CA=4,则 的值为【 】
A. B. C. D.
7. 北京市环保检测中心网站公布的2012年3月31日的PM2.5研究性检测部分数据如下表:
时间
0:00
4:00
8:00
12:00
16:00
20:00
PM2.5(mg/m3)
0.027
0.035
0.032
0.014
0.016
0.032
则该日这6个时刻的PM2.5的众数和中位数分别是【 】
A. 0.032, 0.0295 B. 0.026, 0.0295 C. 0.026, 0.032 D. 0.032, 0.027
8.下列图形中,能通过折叠围成一个三棱柱的是【 】
A B C D
9.函数y=的自变量的取值范围是 .
10.分解因式:x3 - 4x= .
11. 右图是某超市一层到二层滚梯示意图.其中AB、CD分别
表示超市一层、二层滚梯口处地面的水平线, ∠ABC=150°,
BC的长约为12米,则乘滚梯从点B到点C上升的高度h
约为 米.
12. 在平面直角坐标系xOy中, 正方形A1B1C1O、
A2B2C2B1、A3B3C3B2, …,按右图所示的方
式放置. 点A1、A2、A3, …和 B1、B2、B3, …
分别在直线y=kx+b和x轴上. 已知C1(1, -1),
C 2(), 则点A3的坐标是 ;
点An的坐标是 .
三、解答题
13.计算:.14.解不等式组:
15. 如图,AC//FE, 点F、C在BD上,AC=DF, BC=EF.
求证:AB=DE.
16.如图,△ABC内接于⊙O, AD是⊙O直径, E是CB延长线上一点, 且(BAE=(C.
(1)求证:直线AE是⊙O的切线;
(2)若EB=AB , , AE=24,求EB的长及⊙O的半径.
能力训练(2)
1.(2012年江西南昌十五校联考)将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1.在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.2
2.(2012年上海市黄浦二模)如图3,在Rt中,,点在上,且,,若将绕点顺时针旋转得到Rt,且落在的延长线上,联结交的延长线于点,则= .
3.(河南省信阳市二中).如图,在等腰梯形中,,=4=,=45°.直角三角板含45°角的顶点在边上移动,一直角边始终经过点,斜边与交于点.若为等腰三角形,则的长等于
4.(2012年,辽宁省营口市)直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为,则的值是___。
5.(2012年广东模拟)如图,将边长为的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交于点M、N,DFAB,垂足为D,AD=2.设△DBE的面积为,则重叠部分的面积为 .(用含S的式子表示)
6.甲学校到丙学校要经过乙学校. 从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了B1线路的概率是多少?
7.如图,在△ABC中,AB=AC,以AB边的中点O为圆心,线段OA的长为半径作圆,分别交BC、AC边于点D、E,DF⊥AC于点F,延长FD交AB延长线于点G .
(1)求证:FD是⊙O的切线.
(2)若BC=AD=4,求的值.
8.阅读下列材料:
问题:如图1,P为正方形ABCD内一点,且PA∶PB∶PC=1∶2∶3,求∠APB的度数.
小娜同学的想法是:不妨设PA=1, PB=2,PC=3,设法把PA、PB、PC相对集中,于是他将△BCP绕点B顺时针旋转90°得到△BAE(如图2),然后连结PE,问题得以解决.
请你回答:图2中∠APB的度数为 .
请你参考小娜同学的思路,解决下列问题:
如图3,P是等边三角形ABC内一点,已知∠APB=115°,∠BPC=125°.
(1)在图3中画出并指明以PA、PB、PC的长度为三边长的一个三角形(保留画图痕迹);
(2)求出以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于 .
图1 图2 图3
9.(2012山东省德州四模)如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC = 4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
⑴当x为何值时,△APD是等腰三角形?
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
10. 有两张完全重合的矩形纸片,小亮将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连结BD、MF,此时他测得BD=8cm,∠ADB=30°.
(1)在图1中,请你判断直线FM和BD是否垂直?并证明你的结论;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少.
11.24.已知:如图,D为线段AB上一点(不与点A、B重合),CD⊥AB,且CD=AB,AE⊥AB,BF⊥AB,且AE=BD,BF=AD.
(1)如图1,当点D恰是AB的中点时,请你猜想并证明∠ACE与∠BCF的数量关系;
(2)如图2,当点D不是AB的中点时,你在(1)中所得的结论是否发生变化,写出你的猜想并证明;
(3)若∠ACB=,直接写出∠ECF的度数(用含的式子表示).
图1 图2
12.如图,将矩形OABC置于平面直角坐标系xOy中,A(,0),C(0,2).
(1) 抛物线经过点B、C,求该抛物线的解析式;
(2)将矩形OABC绕原点顺时针旋转一个角度(0°<<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标;
(3)如图(2),将矩形OABC绕原点顺时针旋转一个角度(0°<<180°),将得到矩形OA’B’C’,设A’C’的中点为点E,联结CE,当 °时,线段CE的长度最大,最大值为 .
13.如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=,直线y=经过点C,交y轴于点G。
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=上且经过点C、D的抛物线的
解析式;
(3)将(2)中的抛物线沿直线y=平移,平移
后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说明
理由。
如图,△ABC, △DCE,△GEF都是正三角形,且B,C,E,F在同一直线上,A,D,G也在同一直线上, 设△ABC, △DCE,△GEF的面积分别为.当时, _________
18.有依次排列的3个数:2,8,7.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2,6,8,-1,7,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:2,4,6,2,8,-9,-1,8,7;继续依次操作下去……,那么从数串2,8,7开始操作第100次后所产生的那个新数串的所有数之和是 .
8.已知:如图,P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,BC∥OP交⊙O于点C.
(1)判断直线PC与⊙O的位置关系,并证明你的结论;
(2)若BC=2,,求PC的长及点C到PA的距离.
同课章节目录
