北师大版小学六年级数学下册《练习一》习题课件(共15张PPT)
文档属性
| 名称 | 北师大版小学六年级数学下册《练习一》习题课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
练 习 一
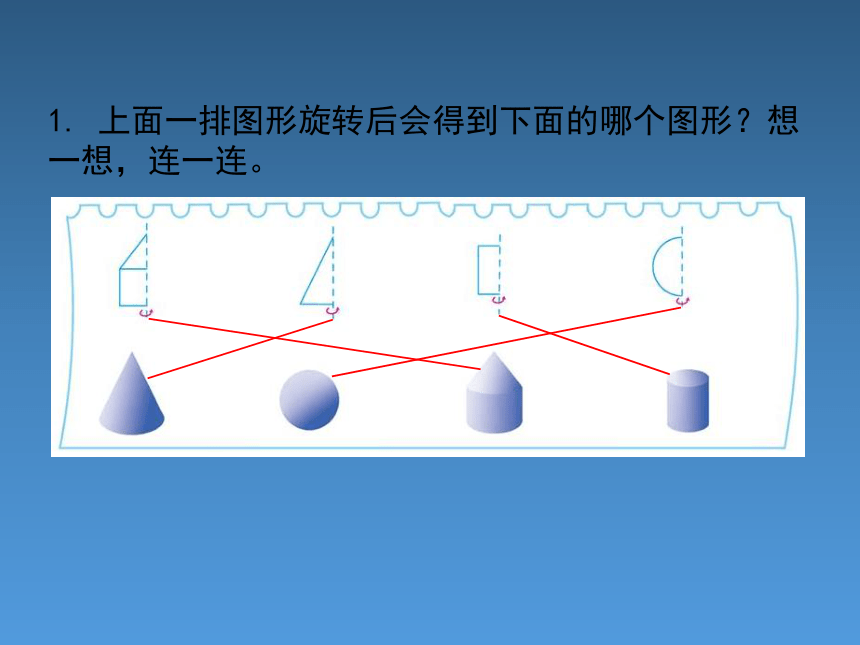
1. 上面一排图形旋转后会得到下面的哪个图形?想一想,连一连。
2. 计算下面图形的体积。
3.14×3 ×6.5=183.69(cm )
×3.14×(8÷2) ×6=100.48(cm )
1
3
8×5×6.5=260(cm )
4×4×4=64(cm )
3.
3.5m =( )dm
3400cm =( )dm
2300dm =( )m
6.5L=( )mL
0.083m =( )dm
4000mL=( )cm =( )dm
350
34
2.3
6500
83
4000
4
4. 一个圆柱形城堡,底面周长是125.6m,高是15m,这个城堡的体积是多少立方米?
125.6÷3.14÷2=20(m)
3.14×20 ×15=18840(m )
答:这个城堡的体积是18840立方米。
5.
(1)包装这个糖果盒的侧面,至少需要多大面积的 纸?
(2)这个糖果盒的体积是多少?
(1)3.14×2×7=43.96(cm )
答:包装这个糖果盒的侧面,至少需要43.96cm 的纸。
(2)3.14×(2÷2) ×7=21.98(cm )
答:这个糖果盒的体积是21.98cm
6. 油桶的表面要刷漆,每平方米需油漆0.6kg。每个油桶的底面直径是40cm,高是60cm,刷100个油桶需要多少油漆?
40cm=0.4m
60cm=0.6m
3.14×(0.4÷2) ×2=0.2512(m )
3.14×0.4×0.6=0.7536(m )
0.2512+0.7536=1.0048(m )
1.0048×100×0.6=60.288(kg)
答:刷100个油桶需要60.288kg油漆。
7. 下面三幅图分别是什么立体图形的展开图?请在括号里填出立体图形的名称,并计算出这个立体图形的表面积。(单位:cm)
长方体
表面积5400cm
正方体
表面积150cm
圆柱体
表面积244.92cm
8. 如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?
甲、乙两个圆柱体的底和高都是相等的,所以甲容器的体积是乙容器的 ,这样甲容器的水注入乙容器后,只注了乙容器的 ,12× =4(cm)。
答:这时乙容器中的水有4厘米高。
1
3
1
3
1
3
9. 如图,圆柱形铁柱有多高?(单位:cm,结果保留整数)
50×20×10=10000(cm )
10000÷(3.14×10 )≈32(cm)
答:圆柱形铁柱高约32厘米。
10. 一个粮仓如右图,如果每立方米粮食的质量为700kg,这个粮仓最多能装多少千克粮食?
圆锥的容积:
1
3
×3.14×(2÷2) ×0.6=0.628(m )
圆柱的容积:3.14×(2÷2) ×1.5=4.71(m )
粮食的质量:(0.628+4.71)×700=3736.5(kg)
答:这个粮仓最多能装3736.5kg粮食。
11. 长方体、正方体和圆柱的体积都可以用“v=sh”计算。想一想,右面两个图形的体积也可以用“v=sh”计算吗?说一说你的想法。
12. 实践活动。
准备六张长16cm、宽4cm的长方形纸。做一做,想一想。
(1)拿出两张长方形纸,一张横着卷成圆柱形,另一张竖着卷成圆柱形。两个圆柱的体积一样大吗?猜一猜,再算一算。(结果保留2位小数)
横着卷成的圆柱的底面半径是2.55cm,体积约是81.67cm ;
竖着卷成的圆柱的底面半径是0.64cm,体积约是20.58cm 。
因此,横着卷成的圆柱体的体积要大。
(2)再拿出两张长方形纸,分别按照下面的步骤做一做。
得到的两个圆柱的体积一样大吗?量一量,算一算。(结果保留2位小数)
图①中卷成底面周长是2cm的圆柱,底面半径是0.32cm,体积约1.29cm ;
图②中卷成底面周长是8cm的圆柱,底面半径是1.27cm,体积约40.52cm 。
因此,得到的两个圆柱体的体积不一样大。
(3)汇总四个圆柱的有关数据,按底面半径从小到大的顺序填入下表中,你发现了什么?
(4)再拿出两张纸,按照不同的方式剪一剪、卷一卷,得到不同的圆柱。想一想,在活动(3)中发现的结论还成立吗?
0.32
2
32
64
10.29
0.64
4
16
64
20.58
64
40.52
81.67
64
8
4
8
16
1.27
2.55
当侧面积一定是,越是细、长的圆柱体积越小,越是粗、矮的圆柱体积越大。
练 习 一
1. 上面一排图形旋转后会得到下面的哪个图形?想一想,连一连。
2. 计算下面图形的体积。
3.14×3 ×6.5=183.69(cm )
×3.14×(8÷2) ×6=100.48(cm )
1
3
8×5×6.5=260(cm )
4×4×4=64(cm )
3.
3.5m =( )dm
3400cm =( )dm
2300dm =( )m
6.5L=( )mL
0.083m =( )dm
4000mL=( )cm =( )dm
350
34
2.3
6500
83
4000
4
4. 一个圆柱形城堡,底面周长是125.6m,高是15m,这个城堡的体积是多少立方米?
125.6÷3.14÷2=20(m)
3.14×20 ×15=18840(m )
答:这个城堡的体积是18840立方米。
5.
(1)包装这个糖果盒的侧面,至少需要多大面积的 纸?
(2)这个糖果盒的体积是多少?
(1)3.14×2×7=43.96(cm )
答:包装这个糖果盒的侧面,至少需要43.96cm 的纸。
(2)3.14×(2÷2) ×7=21.98(cm )
答:这个糖果盒的体积是21.98cm
6. 油桶的表面要刷漆,每平方米需油漆0.6kg。每个油桶的底面直径是40cm,高是60cm,刷100个油桶需要多少油漆?
40cm=0.4m
60cm=0.6m
3.14×(0.4÷2) ×2=0.2512(m )
3.14×0.4×0.6=0.7536(m )
0.2512+0.7536=1.0048(m )
1.0048×100×0.6=60.288(kg)
答:刷100个油桶需要60.288kg油漆。
7. 下面三幅图分别是什么立体图形的展开图?请在括号里填出立体图形的名称,并计算出这个立体图形的表面积。(单位:cm)
长方体
表面积5400cm
正方体
表面积150cm
圆柱体
表面积244.92cm
8. 如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?
甲、乙两个圆柱体的底和高都是相等的,所以甲容器的体积是乙容器的 ,这样甲容器的水注入乙容器后,只注了乙容器的 ,12× =4(cm)。
答:这时乙容器中的水有4厘米高。
1
3
1
3
1
3
9. 如图,圆柱形铁柱有多高?(单位:cm,结果保留整数)
50×20×10=10000(cm )
10000÷(3.14×10 )≈32(cm)
答:圆柱形铁柱高约32厘米。
10. 一个粮仓如右图,如果每立方米粮食的质量为700kg,这个粮仓最多能装多少千克粮食?
圆锥的容积:
1
3
×3.14×(2÷2) ×0.6=0.628(m )
圆柱的容积:3.14×(2÷2) ×1.5=4.71(m )
粮食的质量:(0.628+4.71)×700=3736.5(kg)
答:这个粮仓最多能装3736.5kg粮食。
11. 长方体、正方体和圆柱的体积都可以用“v=sh”计算。想一想,右面两个图形的体积也可以用“v=sh”计算吗?说一说你的想法。
12. 实践活动。
准备六张长16cm、宽4cm的长方形纸。做一做,想一想。
(1)拿出两张长方形纸,一张横着卷成圆柱形,另一张竖着卷成圆柱形。两个圆柱的体积一样大吗?猜一猜,再算一算。(结果保留2位小数)
横着卷成的圆柱的底面半径是2.55cm,体积约是81.67cm ;
竖着卷成的圆柱的底面半径是0.64cm,体积约是20.58cm 。
因此,横着卷成的圆柱体的体积要大。
(2)再拿出两张长方形纸,分别按照下面的步骤做一做。
得到的两个圆柱的体积一样大吗?量一量,算一算。(结果保留2位小数)
图①中卷成底面周长是2cm的圆柱,底面半径是0.32cm,体积约1.29cm ;
图②中卷成底面周长是8cm的圆柱,底面半径是1.27cm,体积约40.52cm 。
因此,得到的两个圆柱体的体积不一样大。
(3)汇总四个圆柱的有关数据,按底面半径从小到大的顺序填入下表中,你发现了什么?
(4)再拿出两张纸,按照不同的方式剪一剪、卷一卷,得到不同的圆柱。想一想,在活动(3)中发现的结论还成立吗?
0.32
2
32
64
10.29
0.64
4
16
64
20.58
64
40.52
81.67
64
8
4
8
16
1.27
2.55
当侧面积一定是,越是细、长的圆柱体积越小,越是粗、矮的圆柱体积越大。
