2021-2022学年苏科版八年级数学下册第七章数据的收集、整理、描述课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册第七章数据的收集、整理、描述课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
2022
第七章 数据的收集、整理、描述
八年级下册
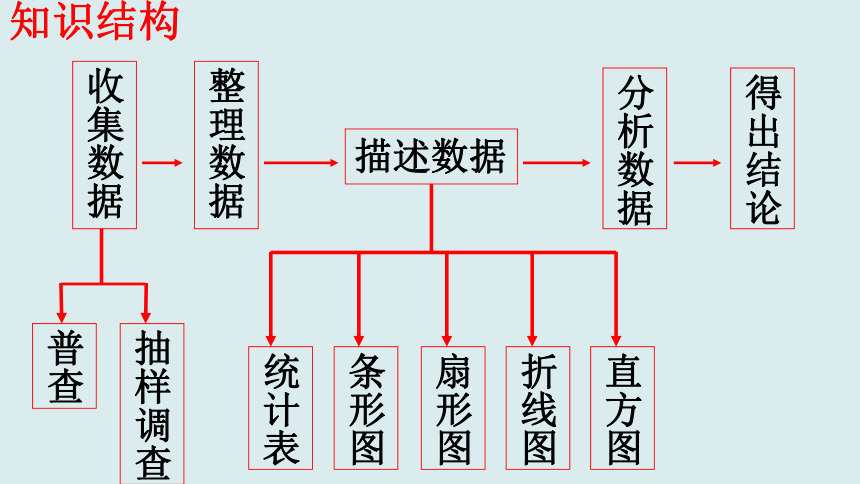
知识结构
收集数据
整理数据
描述数据
条形图
扇形图
折线图
直方图
分析数据
得出结论
统计表
普查
抽样调查
普查:
抽样调查:
为一特定目的而对所有考察对象所做的全面调查。
为一特定目的而对部分考察对象所做的调查
相关概念:总体,个体,样本,样本容量。
(1)普查的调查结果准确,但工作量大,难度大,而且有些调查具有破坏性不宜使用普查。
(2)抽样调查的工作量较小,便于进行;但其调查结果不准确,应注意选取的样本的全面性和代表性。
优缺点:
知识回顾
普查与抽样调查
例 1 下列调查中,调查方式选择更合适的是 ( )
D.为了解一批灯泡的使用寿命,选择抽样调查
A.为了解某公园全年的游客流量,选择普查
B.为了解生产的1 000枚炮弹的杀伤半径,选择普查
C.对“天宫二号”空间实验室零部件的检查,选择抽样调查
D
调查对象多,适合抽样调查
具有破坏性,适合抽样调查
涉及重大安全问题,适合普查
典例分析
关注调查方式的选择
1.要调查下面的问题:
①调查学校营养餐牛奶的质量情况;
②调查你们班学生早餐是否有喝牛奶的习惯;
③调查全国中学生的节水意识;
④调查某校七年级学生的视力情况,
其中适合采用普查的是_______.(填写序号)
②,④
调查对象多,适合抽样调查
具有破坏性,适合抽样调查
巩固小练
关注调查方式的选择
总体、个体、样本、样本容量的理解
典例分析
例2 为了解某校600名八年级学生的身高,随机抽测了100名学生的身高,在这个问题中,
总体是_____________________,
个体是_____________________,
样本是_____________________,
样本容量是________.
该校600名八年级学生
每个八年级学生的身高
从中抽测的100名八年级学生的身高
100
样本容量是数值,无单位
考察对象是指“数”,而不是“物”
×
×
的身高的全体
名
1.为了了解我市2019年40 000名考生的数学中考成绩,从中抽取
了2 000名考生的成绩进行统计,在这个问题中,下列说法:
①这40 000名考生的数学中考成绩的全体是总体;
②每个考生是个体;
③从中抽取的2 000名考生的数学中考成绩是总体的一个样本;
④样本容量是2 000.
其中说法正确的有___________.(填序号)
每个考生的数学中考成绩是个体
√
√
√
①,③,④
总体、个体、样本、样本容量的理解
巩固练习
×
知识回顾
扇形统计图的制作及分析
扇形圆心角度数=该部分百分比×3600
绘制扇形统计图的步骤:
1.算比例;
(计算各部分占总体的百分比)
2.求角度;
(求出各个扇形的圆心角度数)
3.画扇形;
(根据圆心角度数在圆中画出各个扇形)
4.标名称;
(标上相应名称与百分比)
1、某班有50人,其中三好学生10人,优秀学生干部5人,在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是( )
A.720,360 B.1000,500
C.1200,600 D.800,400
2、如图,某校共有学生700人,图中扇形A、B、C、分别表示参加语、数、英三个兴趣小组的人数的百分比,规定每人只能参加一个兴趣小组且每人均参加课外小组,则不参加数学小组的学生有( )
A.441人 B.259人
C.451人 D.249人
A
A
巩固练习
扇形统计图的制作及分析
知识回顾
统计图的特点及选用
条形统计图
能清楚 地表示出每个项目的具体数目。
折线统计图
能清楚 地反映事物的变化情况。
扇形统计图能清楚地表示出各部分在总体中所占的百分比。
1、要清楚地表明一病人的体温变化情况,应选择的统计图是( )
A.扇形统计图 B.条形统计图
C.折线统计图 D.以上都不是
2、某音乐行出售三种音乐CD,即古典音乐、流行音乐、民族音乐,为了表示这三种音乐唱片的销售量的百分比,应该用( )
A.扇形统计图 B.折线统计图
C.条形统计图 D.以上都可以
C
A
巩固练习
统计图的特点及选用
巩固练习
统计图的综合应用
1、某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种乐器),现将收集到的数据绘制成如图所示的两幅不完整的统计图。
(1)这次共抽取 名学生进行调查,扇形统计图中的 x = ;
200
15%
(2)请补全条形统计图:
(3)在扇形统计图中“扬琴”所在扇形的圆心角是 度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有 名.
36
900
60
巩固练习
统计图的综合应用
知识回顾
频数、频率、频数分布直方图
某个对象出现的次数
频数:
频率:
频数与总次数的比值
频率 =
频数
总次数
频数=
总次数×频率
总次数=
频数
频率
各个对象出现的频数之和等于总次数.
各个对象出现的频率之和等于1.
1.算:计算最大值与最小值的差
2.定:决定组距与组数
3.划:利用划记法
得到各组频数
4.列:列出频率分布表
5.绘:绘制出直方图
绘制频数分布直方图的基本步骤:
知识回顾
频数、频率、频数分布直方图
1、已知一个样本:
27,23,25,27,29,31,27,30,32,28,31,28,26,27,29,28,24,26,27,30
那么频数为 8 的范围是( )
A .24.5 ~26.5 B.26.5~28.5
C.28.5~30.5 D.30.5~32.5
2、在1000个数据中,用适当的方法抽取50个作为样本进行统计,频率分布表中54.5~57.5这一组的频率是0. 12,那么估计总体数据落在54.5~57.5 之间的约有( )
A.120个 B.60个
C.12个 D.6个
B
A
巩固练习
频数、频率、频数分布直方图
3、某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
根据以上图表信息,
解答下列问题:
(1)表中的a=_____,
b=______;
(2)请把频数分布直方图
补充完整;
(3)若该校共有1 200名
学生,请估计该校在上学
期参加社区活动 超过6次的学生有多少人?
巩固练习
频数、频率、频数分布直方图
12
0.08
12
672
2022
第七章 数据的收集、整理、描述
八年级下册
知识结构
收集数据
整理数据
描述数据
条形图
扇形图
折线图
直方图
分析数据
得出结论
统计表
普查
抽样调查
普查:
抽样调查:
为一特定目的而对所有考察对象所做的全面调查。
为一特定目的而对部分考察对象所做的调查
相关概念:总体,个体,样本,样本容量。
(1)普查的调查结果准确,但工作量大,难度大,而且有些调查具有破坏性不宜使用普查。
(2)抽样调查的工作量较小,便于进行;但其调查结果不准确,应注意选取的样本的全面性和代表性。
优缺点:
知识回顾
普查与抽样调查
例 1 下列调查中,调查方式选择更合适的是 ( )
D.为了解一批灯泡的使用寿命,选择抽样调查
A.为了解某公园全年的游客流量,选择普查
B.为了解生产的1 000枚炮弹的杀伤半径,选择普查
C.对“天宫二号”空间实验室零部件的检查,选择抽样调查
D
调查对象多,适合抽样调查
具有破坏性,适合抽样调查
涉及重大安全问题,适合普查
典例分析
关注调查方式的选择
1.要调查下面的问题:
①调查学校营养餐牛奶的质量情况;
②调查你们班学生早餐是否有喝牛奶的习惯;
③调查全国中学生的节水意识;
④调查某校七年级学生的视力情况,
其中适合采用普查的是_______.(填写序号)
②,④
调查对象多,适合抽样调查
具有破坏性,适合抽样调查
巩固小练
关注调查方式的选择
总体、个体、样本、样本容量的理解
典例分析
例2 为了解某校600名八年级学生的身高,随机抽测了100名学生的身高,在这个问题中,
总体是_____________________,
个体是_____________________,
样本是_____________________,
样本容量是________.
该校600名八年级学生
每个八年级学生的身高
从中抽测的100名八年级学生的身高
100
样本容量是数值,无单位
考察对象是指“数”,而不是“物”
×
×
的身高的全体
名
1.为了了解我市2019年40 000名考生的数学中考成绩,从中抽取
了2 000名考生的成绩进行统计,在这个问题中,下列说法:
①这40 000名考生的数学中考成绩的全体是总体;
②每个考生是个体;
③从中抽取的2 000名考生的数学中考成绩是总体的一个样本;
④样本容量是2 000.
其中说法正确的有___________.(填序号)
每个考生的数学中考成绩是个体
√
√
√
①,③,④
总体、个体、样本、样本容量的理解
巩固练习
×
知识回顾
扇形统计图的制作及分析
扇形圆心角度数=该部分百分比×3600
绘制扇形统计图的步骤:
1.算比例;
(计算各部分占总体的百分比)
2.求角度;
(求出各个扇形的圆心角度数)
3.画扇形;
(根据圆心角度数在圆中画出各个扇形)
4.标名称;
(标上相应名称与百分比)
1、某班有50人,其中三好学生10人,优秀学生干部5人,在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是( )
A.720,360 B.1000,500
C.1200,600 D.800,400
2、如图,某校共有学生700人,图中扇形A、B、C、分别表示参加语、数、英三个兴趣小组的人数的百分比,规定每人只能参加一个兴趣小组且每人均参加课外小组,则不参加数学小组的学生有( )
A.441人 B.259人
C.451人 D.249人
A
A
巩固练习
扇形统计图的制作及分析
知识回顾
统计图的特点及选用
条形统计图
能清楚 地表示出每个项目的具体数目。
折线统计图
能清楚 地反映事物的变化情况。
扇形统计图能清楚地表示出各部分在总体中所占的百分比。
1、要清楚地表明一病人的体温变化情况,应选择的统计图是( )
A.扇形统计图 B.条形统计图
C.折线统计图 D.以上都不是
2、某音乐行出售三种音乐CD,即古典音乐、流行音乐、民族音乐,为了表示这三种音乐唱片的销售量的百分比,应该用( )
A.扇形统计图 B.折线统计图
C.条形统计图 D.以上都可以
C
A
巩固练习
统计图的特点及选用
巩固练习
统计图的综合应用
1、某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种乐器),现将收集到的数据绘制成如图所示的两幅不完整的统计图。
(1)这次共抽取 名学生进行调查,扇形统计图中的 x = ;
200
15%
(2)请补全条形统计图:
(3)在扇形统计图中“扬琴”所在扇形的圆心角是 度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有 名.
36
900
60
巩固练习
统计图的综合应用
知识回顾
频数、频率、频数分布直方图
某个对象出现的次数
频数:
频率:
频数与总次数的比值
频率 =
频数
总次数
频数=
总次数×频率
总次数=
频数
频率
各个对象出现的频数之和等于总次数.
各个对象出现的频率之和等于1.
1.算:计算最大值与最小值的差
2.定:决定组距与组数
3.划:利用划记法
得到各组频数
4.列:列出频率分布表
5.绘:绘制出直方图
绘制频数分布直方图的基本步骤:
知识回顾
频数、频率、频数分布直方图
1、已知一个样本:
27,23,25,27,29,31,27,30,32,28,31,28,26,27,29,28,24,26,27,30
那么频数为 8 的范围是( )
A .24.5 ~26.5 B.26.5~28.5
C.28.5~30.5 D.30.5~32.5
2、在1000个数据中,用适当的方法抽取50个作为样本进行统计,频率分布表中54.5~57.5这一组的频率是0. 12,那么估计总体数据落在54.5~57.5 之间的约有( )
A.120个 B.60个
C.12个 D.6个
B
A
巩固练习
频数、频率、频数分布直方图
3、某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
根据以上图表信息,
解答下列问题:
(1)表中的a=_____,
b=______;
(2)请把频数分布直方图
补充完整;
(3)若该校共有1 200名
学生,请估计该校在上学
期参加社区活动 超过6次的学生有多少人?
巩固练习
频数、频率、频数分布直方图
12
0.08
12
672
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
