辽宁省沈阳市第二十中学2013届高三高考领航考试(四)数学(文)试题
文档属性
| 名称 | 辽宁省沈阳市第二十中学2013届高三高考领航考试(四)数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 606.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-17 00:00:00 | ||
图片预览




文档简介
沈阳市第二十中学2013届高考领航试卷(4)
出题人: 审题人:
一 、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数,则的大小关系是( )
(A) (B)
(C) (D)
2.过点P(0,-2)的双曲线C的一个焦点与抛物线的焦点相同,则双曲线C的标准方程是( )
(A) (B)
(C) (D)
3.已知函数,则函数的零点个数是( )
(A) 4 (B) 3 (C) 2 (D) 1
4.函数的零点所在的区间为
A. B. C.( D.
5.某人睡午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待时间不多于15分钟的概率为
A. B. C. D.
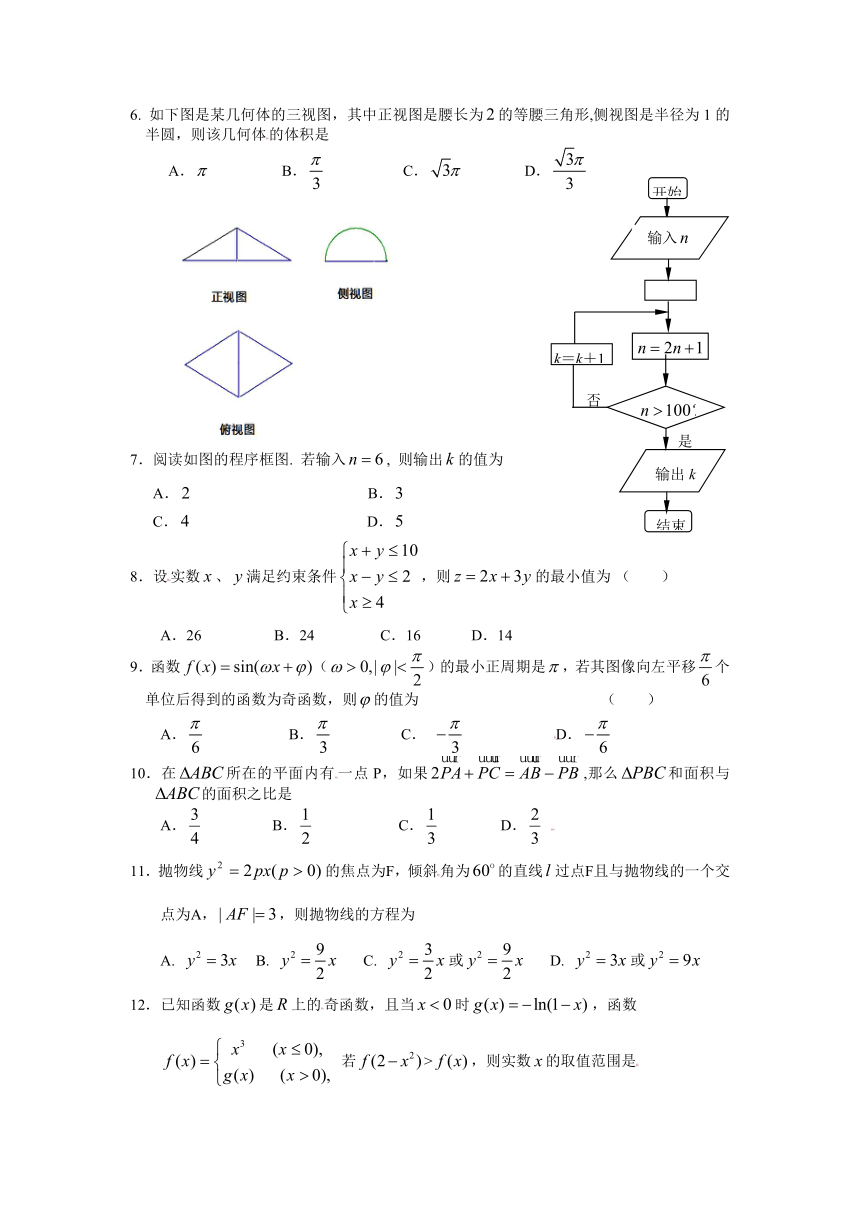
6. 如下图是某几何体的三视图,其中正视图是腰长为的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是
A. B. C. D.
7.阅读如图的程序框图. 若输入, 则输出的值为
A. B.
C. D.
8.设实数、满足约束条件,则的最小值为 ( )
A.26 B.24 C.16 D.14
9.函数()的最小正周期是,若其图像向左平移个单位后得到的函数为奇函数,则的值为 ( )
A. B. C. D.
10.在所在的平面内有一点P,如果,那么和面积与的面积之比是
A. B. C. D.
11.抛物线的焦点为F,倾斜角为的直线过点F且与抛物线的一个交点为A,,则抛物线的方程为
A. B. C. 或 D. 或
12.已知函数是上的奇函数,且当时,函数
若>,则实数的取值范围是
A. B.
C.(1,2) D.
二、填空题:本大题共4个小题,每小题5分,共20分
13.从某地区随机抽取100名高中男生,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从各组内的男生中,用分层抽样的方法选取20人参加一项活动,则从这一组中抽取的人数为 .
14.在中,若,则的面积S= .
15.将边长为2的正沿边上的高折成直二面角,则三棱锥的外接球的表面积为 .
16.已知圆C的圆心在轴上,曲线在点处的切线恰与圆C在点处相切,则圆C的方程为 .
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知正项等差数列的前项和为,且满足,.
(Ⅰ)求数列的通项公式;
(Ⅱ)若数列满足且,求数列的前项和.
18. 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国标准采用世卫组织设定的最宽限值,日均值在35微克/立方米以下空气质量为一级;在35微克/立方米75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2011年全年每天的监测数据中随机抽取6天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这6天的数据中随机抽出2天.
(Ⅰ)求恰有一天空气质量超标的概率;
(Ⅱ)求至多有一天空气质量超标的概率.
19.已知四棱锥的底面为菱形,且,
,为的中点.
(Ⅰ)求证:平面;
(Ⅱ)求点到面的距离.
20.已知椭圆的短轴长等于焦距,椭圆C上的点到右焦点的最短距离为.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点且斜率为的直线与交于、两点,是点关于轴的对称点,证明:三点共线.
21.已知函数
(Ⅰ)当时,求的单调区间;
(Ⅱ)若对任意, 恒成立,求实数的取值范围.
请考生在22, 23,24三题中任选一题作答,如果多做,则按所做的第一题记分,做答时,请写清题号.
22.(本小题满分10分)选修4—1:几何证明选讲
如图所示,已知AB是圆的直径,AC是弦,,垂足为D,AC平分
(Ⅰ)求证:直线CE是圆的切线;
(Ⅱ)求证:
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与轴的正半轴重合.
直线的参数方程为:(t为参数),曲线的极坐标方程为:.
(Ⅰ)写出的直角坐标方程,并指出是什么曲线;
(Ⅱ)设直线与曲线相交于、两点,求值.
24.(本小题满分10分)选修4-5:不等式选讲
已知函数.
(Ⅰ)当时,求函数的定义域;
(Ⅱ)若关于的不等式的解集是,求的取值范围.
沈阳市第二十中学2013届高考领航试卷(文)
参考答案及评分标准
一、选择题: BCACB DBDCA DD[来源:21世纪教育网]
二、填空题 13. 6 14.. 15.. 16..
三、解答题
17.(本小题共12分)21世纪教育网
解:(Ⅰ) 是等差数列且,,
又.…………………………………………………2分
,……………………………4分
,. ………………6分
(Ⅱ),
当时,
,……………………8分
当时,满足上式,
……………………………………………………10分
. ………………………………………………12分
18.(本小题共12分)
解: 由茎叶图知:6天有4天空气质量未超标,有2天空气质量超标. …………2分
记未超标的4天为,超标的两天为.则从6天中抽取2天的所有情况为:,,,,,,,,,,,,,,,基本事件数为15.…………4分[来源:21世纪教育网]
(Ⅰ)记 “6天中抽取2天,恰有1天空气质量超标”为事件,可能结果为:,,,,,,,,基本事件数为.
∴;……………6分
(Ⅱ)记“至多有一天空气质量超标”为事件,
“2天都超标”为事件,其可能结果为,…………………………8分
故,…………………………………………………………10分
∴. …………………………………12分
19.(本小题共12分)(I)证明:连接
为等腰直角三角形
为的中点
……………………2分
又
是等边三角形
,………………………………4分
又
,即21世纪教育网
……………………6分
(II)设点到面的距离为
…………8分
,到面的距离
………………………………10分
点到面的距离为……………………12分
20.(本小题共12分)(I)由题可知: …………2分
解得,
椭圆C的方程为…………………………4分
(II)设直线:,,,,,
由得.…………6分
所以,. ……………………8分
而
,,…………10分
∴三点共线 ……………………………………12分
21.(本小题共12分)(I)当时,
………………………………………………………………2分 由得得
的单调递增区间为,单调递减区间为.………………4分
(II)若对任意, 使得恒成立, 则时,恒成立,
即时,恒成立………………………………6分
设,,则 ,
设, 在上恒成立
在上单调递增
即在上单调递增………………8分
,
在有零点在上单调递减,在上单调递增……………10分
,即,……………………12分
22.(本小题共10分)
证明:(Ⅰ)连接,因为,所以. 2分又因为,所以,
又因为平分,所以, 4分
所以,即,所以是的切线. 6分
(Ⅱ)连接,因为是圆的直径,所以,
因为, 8分
所以△∽△,所以,即. 10分
23.(本小题共10分)
解:(Ⅰ),
,………………………………………………………………2分
由得:
所以曲线的直角坐标方程为,…………………………4分
它是以为圆心,半径为的圆. …………………………………………5分
(Ⅱ)把代入整理得,……7分
设其两根分别为、,则,…………………………8分
……………………………………10分
另解:
化直线参数方程为普通方程,然后求圆心到直线距离,再用垂径定理求得的值.
24.解:(Ⅰ)由题设知:,
不等式的解集是以下不等式组解集的并集:
,或,或………………3分
解得函数的定义域为; ………………………………5分
(Ⅱ)不等式即,21世纪教育网
时,恒有,…………………………8分[来源:21世纪教育网]
不等式解集是R,
的取值范围是. ……………………………10分
出题人: 审题人:
一 、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数,则的大小关系是( )
(A) (B)
(C) (D)
2.过点P(0,-2)的双曲线C的一个焦点与抛物线的焦点相同,则双曲线C的标准方程是( )
(A) (B)
(C) (D)
3.已知函数,则函数的零点个数是( )
(A) 4 (B) 3 (C) 2 (D) 1
4.函数的零点所在的区间为
A. B. C.( D.
5.某人睡午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待时间不多于15分钟的概率为
A. B. C. D.
6. 如下图是某几何体的三视图,其中正视图是腰长为的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是
A. B. C. D.
7.阅读如图的程序框图. 若输入, 则输出的值为
A. B.
C. D.
8.设实数、满足约束条件,则的最小值为 ( )
A.26 B.24 C.16 D.14
9.函数()的最小正周期是,若其图像向左平移个单位后得到的函数为奇函数,则的值为 ( )
A. B. C. D.
10.在所在的平面内有一点P,如果,那么和面积与的面积之比是
A. B. C. D.
11.抛物线的焦点为F,倾斜角为的直线过点F且与抛物线的一个交点为A,,则抛物线的方程为
A. B. C. 或 D. 或
12.已知函数是上的奇函数,且当时,函数
若>,则实数的取值范围是
A. B.
C.(1,2) D.
二、填空题:本大题共4个小题,每小题5分,共20分
13.从某地区随机抽取100名高中男生,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从各组内的男生中,用分层抽样的方法选取20人参加一项活动,则从这一组中抽取的人数为 .
14.在中,若,则的面积S= .
15.将边长为2的正沿边上的高折成直二面角,则三棱锥的外接球的表面积为 .
16.已知圆C的圆心在轴上,曲线在点处的切线恰与圆C在点处相切,则圆C的方程为 .
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知正项等差数列的前项和为,且满足,.
(Ⅰ)求数列的通项公式;
(Ⅱ)若数列满足且,求数列的前项和.
18. 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国标准采用世卫组织设定的最宽限值,日均值在35微克/立方米以下空气质量为一级;在35微克/立方米75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2011年全年每天的监测数据中随机抽取6天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这6天的数据中随机抽出2天.
(Ⅰ)求恰有一天空气质量超标的概率;
(Ⅱ)求至多有一天空气质量超标的概率.
19.已知四棱锥的底面为菱形,且,
,为的中点.
(Ⅰ)求证:平面;
(Ⅱ)求点到面的距离.
20.已知椭圆的短轴长等于焦距,椭圆C上的点到右焦点的最短距离为.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点且斜率为的直线与交于、两点,是点关于轴的对称点,证明:三点共线.
21.已知函数
(Ⅰ)当时,求的单调区间;
(Ⅱ)若对任意, 恒成立,求实数的取值范围.
请考生在22, 23,24三题中任选一题作答,如果多做,则按所做的第一题记分,做答时,请写清题号.
22.(本小题满分10分)选修4—1:几何证明选讲
如图所示,已知AB是圆的直径,AC是弦,,垂足为D,AC平分
(Ⅰ)求证:直线CE是圆的切线;
(Ⅱ)求证:
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与轴的正半轴重合.
直线的参数方程为:(t为参数),曲线的极坐标方程为:.
(Ⅰ)写出的直角坐标方程,并指出是什么曲线;
(Ⅱ)设直线与曲线相交于、两点,求值.
24.(本小题满分10分)选修4-5:不等式选讲
已知函数.
(Ⅰ)当时,求函数的定义域;
(Ⅱ)若关于的不等式的解集是,求的取值范围.
沈阳市第二十中学2013届高考领航试卷(文)
参考答案及评分标准
一、选择题: BCACB DBDCA DD[来源:21世纪教育网]
二、填空题 13. 6 14.. 15.. 16..
三、解答题
17.(本小题共12分)21世纪教育网
解:(Ⅰ) 是等差数列且,,
又.…………………………………………………2分
,……………………………4分
,. ………………6分
(Ⅱ),
当时,
,……………………8分
当时,满足上式,
……………………………………………………10分
. ………………………………………………12分
18.(本小题共12分)
解: 由茎叶图知:6天有4天空气质量未超标,有2天空气质量超标. …………2分
记未超标的4天为,超标的两天为.则从6天中抽取2天的所有情况为:,,,,,,,,,,,,,,,基本事件数为15.…………4分[来源:21世纪教育网]
(Ⅰ)记 “6天中抽取2天,恰有1天空气质量超标”为事件,可能结果为:,,,,,,,,基本事件数为.
∴;……………6分
(Ⅱ)记“至多有一天空气质量超标”为事件,
“2天都超标”为事件,其可能结果为,…………………………8分
故,…………………………………………………………10分
∴. …………………………………12分
19.(本小题共12分)(I)证明:连接
为等腰直角三角形
为的中点
……………………2分
又
是等边三角形
,………………………………4分
又
,即21世纪教育网
……………………6分
(II)设点到面的距离为
…………8分
,到面的距离
………………………………10分
点到面的距离为……………………12分
20.(本小题共12分)(I)由题可知: …………2分
解得,
椭圆C的方程为…………………………4分
(II)设直线:,,,,,
由得.…………6分
所以,. ……………………8分
而
,,…………10分
∴三点共线 ……………………………………12分
21.(本小题共12分)(I)当时,
………………………………………………………………2分 由得得
的单调递增区间为,单调递减区间为.………………4分
(II)若对任意, 使得恒成立, 则时,恒成立,
即时,恒成立………………………………6分
设,,则 ,
设, 在上恒成立
在上单调递增
即在上单调递增………………8分
,
在有零点在上单调递减,在上单调递增……………10分
,即,……………………12分
22.(本小题共10分)
证明:(Ⅰ)连接,因为,所以. 2分又因为,所以,
又因为平分,所以, 4分
所以,即,所以是的切线. 6分
(Ⅱ)连接,因为是圆的直径,所以,
因为, 8分
所以△∽△,所以,即. 10分
23.(本小题共10分)
解:(Ⅰ),
,………………………………………………………………2分
由得:
所以曲线的直角坐标方程为,…………………………4分
它是以为圆心,半径为的圆. …………………………………………5分
(Ⅱ)把代入整理得,……7分
设其两根分别为、,则,…………………………8分
……………………………………10分
另解:
化直线参数方程为普通方程,然后求圆心到直线距离,再用垂径定理求得的值.
24.解:(Ⅰ)由题设知:,
不等式的解集是以下不等式组解集的并集:
,或,或………………3分
解得函数的定义域为; ………………………………5分
(Ⅱ)不等式即,21世纪教育网
时,恒有,…………………………8分[来源:21世纪教育网]
不等式解集是R,
的取值范围是. ……………………………10分
同课章节目录
