第二十九章 投影与视图达标检测卷(含答案)
文档属性
| 名称 | 第二十九章 投影与视图达标检测卷(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级下册数学第二十九章达标检测卷
【检测内容:第二十九章 投影与视图 满分:150分】
一、选择题(本大题共10小题,每小题4分,满分40分)
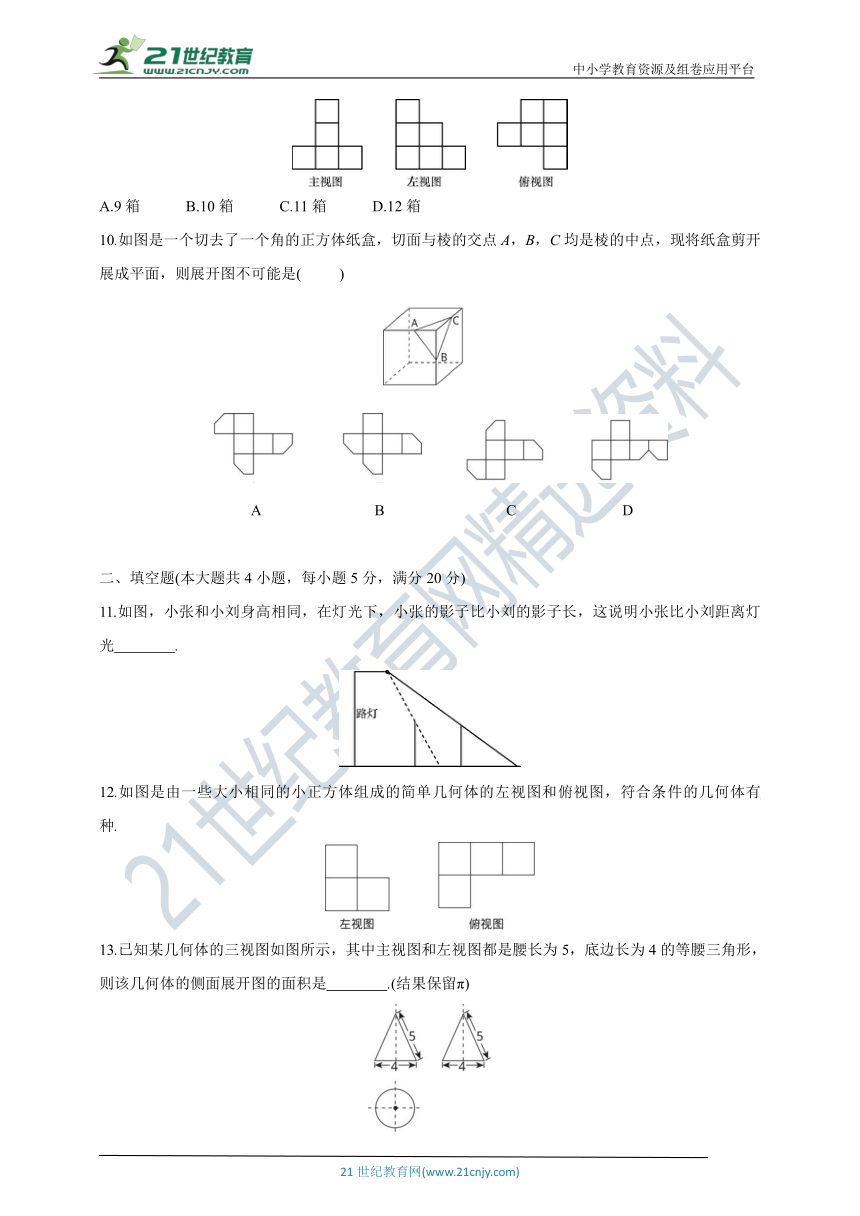
1.球的正投影是( )
A.圆面 B.椭圆面 C.点 D.圆环
2.下图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线 B.灯光光线
C.可能为太阳光线或灯光光线 D.该影子实际不可能存在
3.如图所示的几何体是某一种机械模型,它的主视图是( )
A B C D
4.如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是( )
A B C D
5.如图是由若干个大小相同的正方体组成的几何体的左视图和俯视图,则它的主视图不可能是( )
A B C D
6.如图是某几何体的三视图及相关数据,则下列判断正确的是( )
A.a>c B.b>c C.a2+4b2=c2 D.a2+b2=c2
7.如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
A.主视图会发生改变 B.俯视图会发生改变
C.左视图会发生改变 D.三种视图都会发生改变
8.如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
A B C D
9.在仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有( )
A.9箱 B.10箱 C.11箱 D.12箱
10.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,小张和小刘身高相同,在灯光下,小张的影子比小刘的影子长,这说明小张比小刘距离灯光 .
12.如图是由一些大小相同的小正方体组成的简单几何体的左视图和俯视图,符合条件的几何体有 种.
13.已知某几何体的三视图如图所示,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形,则该几何体的侧面展开图的面积是 .(结果保留π)
14.如图是由几个相同的小正方体搭成的几何体,则
(1)搭成这个几何体需要 个小正方体;
(2)在保持主视图和左视图不变的情况下,最多可以拿掉 个小正方体.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,AB和DE是直立在地面上的两根立柱,AB=4 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8 m,请你计算DE的长.
16.如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)图2是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图.
(2)已知h=4,求a的值和该几何体的表面积.
四、(本大题共2小题,每小题8分,满分16分)
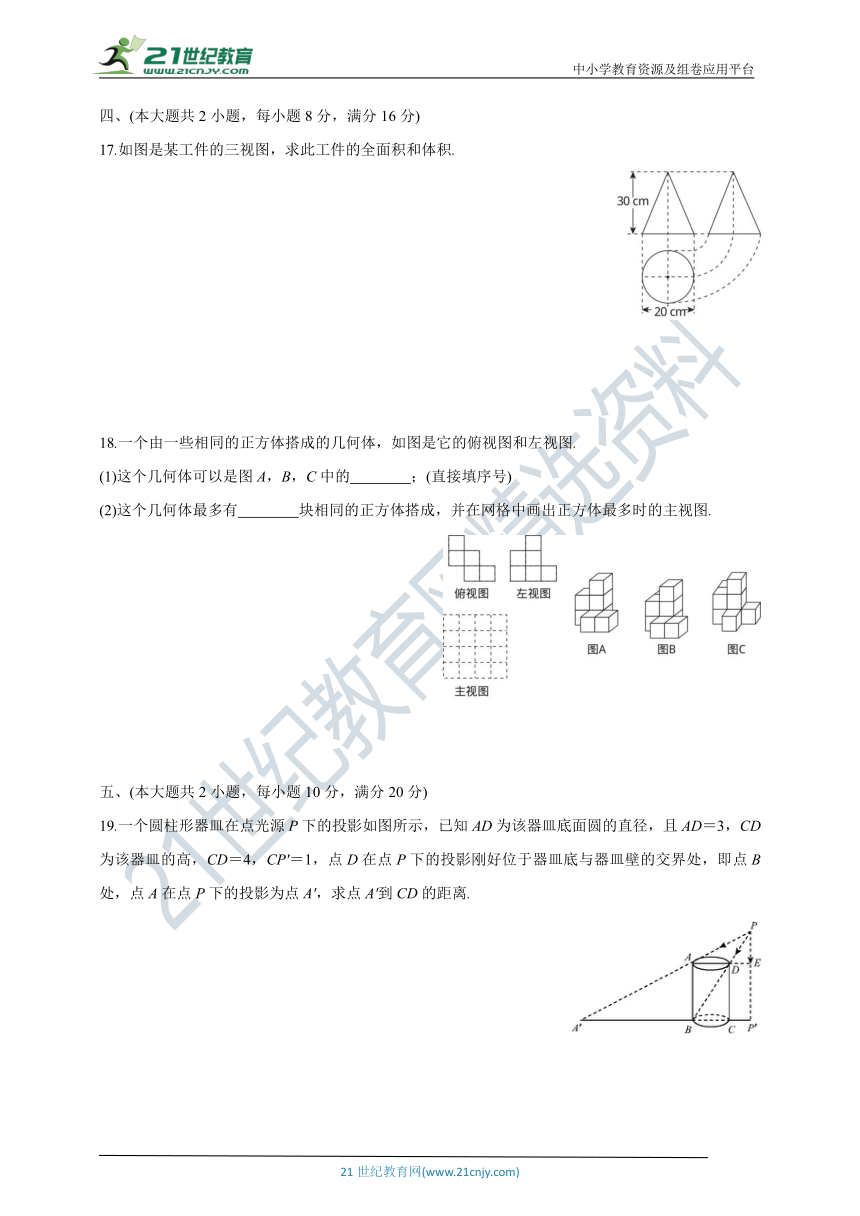
17.如图是某工件的三视图,求此工件的全面积和体积.
18.一个由一些相同的正方体搭成的几何体,如图是它的俯视图和左视图.
(1)这个几何体可以是图A,B,C中的 ;(直接填序号)
(2)这个几何体最多有 块相同的正方体搭成,并在网格中画出正方体最多时的主视图.
五、(本大题共2小题,每小题10分,满分20分)
19.一个圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP'=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为点A',求点A'到CD的距离.
20.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
六、(本题满分12分)
21.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 碟子的高度/cm
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x个碟子时,请写出此时碟子的高度;(用含x的式子表示)
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
七、(本题满分12分)
22.如图,A,B在一条直线上,小明从点A出发沿AB方向匀速前进,4秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到达点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后到达点H,此时他(GH)处于灯光正下方.
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明沿AB方向匀速前进的速度.
八、(本题满分14分)
23.把棱长为1 cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面).
(1)该几何体中有多少个小正方体
(2)画出主视图.
(3)求出涂上颜色部分的总面积.
参 考 答 案
1.A 2.B 3.C 4.D 5.B 6.D 7.A 8.C 9.A 10.B
11.远 12.7 13.10π 14.(1)10 (2)1
15.解:(1)如图,连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE在阳光下的投影.
(2)由(1)知AC∥DF,∴∠ACB=∠DFE.又∵∠ABC=∠DEF=90°,∴△ABC∽△DEF,∴AB∶DE=BC∶EF,即4∶DE=3∶8,解得DE= m.
16.解:(1)如图所示.
(2)根据俯视图和主视图可知a2+a2=h2=42,解得a=2.几何体的表面积为2ah+ah+a2×2=16+24.
17.解:由三视图可知,该工件为底面半径为10 cm,高为30 cm的圆锥体,这圆锥的母线长为=10(cm),圆锥的侧面积为s=πrl=×20π×10=100π(cm2),圆锥的底面积为102π=100π(cm2),圆锥的全面积为100π+100π=100(1+)π(cm2),圆锥的体积为×π×(20÷2)2×30=1000 π(cm3).故此工件的全面积是100(1+)π cm2,体积是1000π cm3.
18.解:(1)B
(2)10 图略.
19.解:根据题意,易证得△APD∽△A'PB,△PDE∽△PBP',∴==.又∵DE=CP'=1,AD=BC=3,将各线段长度代入得=,解得A'B=12,∴点A'到CD的距离为A'B+BC=12+3=15.
20.解:连接CD.由题易知∠B=90°,∠DOE=90°,点O,D,C共线.∵OD=0.8 m,OE=0.8 m,∴∠DEB=45°.∵∠B=90°,∴∠BAE=45°,∴AB=BE,设AB=EB=x m.∵∠B=∠DOE=90°,∴AB∥CO,∴△ABF∽△COF,∴=,即=,解得x=4.4.经检验x=4.4是原方程的解.答:围墙AB的高度是4.4 m.
21.解:(1)2+1.5(x-1)=(1.5x+0.5)m.
(2)由三视图可知共有12个碟子,∴叠成一摞后的高度为1.5×12+0.5=18.5(cm).
22.解:(1)如图所示,FM即为所求.
(2)设速度为x米/秒.根据题意得CG∥AH,∴△COG∽△AOH,∴=,即==.又∵CG∥AH,∴△EOG∽△MOH,∴=,即=,解得x=.答:小明沿AB方向匀速前进的速度为米/秒.
23.解:(1)该几何体中正方体的个数为9+4+1=14.
(2)如图所示.
(3)先算侧面:底层12个小面,中层8个,上层4个,再算上面:上层1个,中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,∴中层是3个),底层是9-4=5(个),总共有33个小面,∴涂上颜色部分的总面积是1×1×33=33(cm2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级下册数学第二十九章达标检测卷
【检测内容:第二十九章 投影与视图 满分:150分】
一、选择题(本大题共10小题,每小题4分,满分40分)
1.球的正投影是( )
A.圆面 B.椭圆面 C.点 D.圆环
2.下图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线 B.灯光光线
C.可能为太阳光线或灯光光线 D.该影子实际不可能存在
3.如图所示的几何体是某一种机械模型,它的主视图是( )
A B C D
4.如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是( )
A B C D
5.如图是由若干个大小相同的正方体组成的几何体的左视图和俯视图,则它的主视图不可能是( )
A B C D
6.如图是某几何体的三视图及相关数据,则下列判断正确的是( )
A.a>c B.b>c C.a2+4b2=c2 D.a2+b2=c2
7.如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
A.主视图会发生改变 B.俯视图会发生改变
C.左视图会发生改变 D.三种视图都会发生改变
8.如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
A B C D
9.在仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有( )
A.9箱 B.10箱 C.11箱 D.12箱
10.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,小张和小刘身高相同,在灯光下,小张的影子比小刘的影子长,这说明小张比小刘距离灯光 .
12.如图是由一些大小相同的小正方体组成的简单几何体的左视图和俯视图,符合条件的几何体有 种.
13.已知某几何体的三视图如图所示,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形,则该几何体的侧面展开图的面积是 .(结果保留π)
14.如图是由几个相同的小正方体搭成的几何体,则
(1)搭成这个几何体需要 个小正方体;
(2)在保持主视图和左视图不变的情况下,最多可以拿掉 个小正方体.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,AB和DE是直立在地面上的两根立柱,AB=4 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8 m,请你计算DE的长.
16.如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)图2是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图.
(2)已知h=4,求a的值和该几何体的表面积.
四、(本大题共2小题,每小题8分,满分16分)
17.如图是某工件的三视图,求此工件的全面积和体积.
18.一个由一些相同的正方体搭成的几何体,如图是它的俯视图和左视图.
(1)这个几何体可以是图A,B,C中的 ;(直接填序号)
(2)这个几何体最多有 块相同的正方体搭成,并在网格中画出正方体最多时的主视图.
五、(本大题共2小题,每小题10分,满分20分)
19.一个圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP'=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为点A',求点A'到CD的距离.
20.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
六、(本题满分12分)
21.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 碟子的高度/cm
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x个碟子时,请写出此时碟子的高度;(用含x的式子表示)
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
七、(本题满分12分)
22.如图,A,B在一条直线上,小明从点A出发沿AB方向匀速前进,4秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到达点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后到达点H,此时他(GH)处于灯光正下方.
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明沿AB方向匀速前进的速度.
八、(本题满分14分)
23.把棱长为1 cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面).
(1)该几何体中有多少个小正方体
(2)画出主视图.
(3)求出涂上颜色部分的总面积.
参 考 答 案
1.A 2.B 3.C 4.D 5.B 6.D 7.A 8.C 9.A 10.B
11.远 12.7 13.10π 14.(1)10 (2)1
15.解:(1)如图,连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE在阳光下的投影.
(2)由(1)知AC∥DF,∴∠ACB=∠DFE.又∵∠ABC=∠DEF=90°,∴△ABC∽△DEF,∴AB∶DE=BC∶EF,即4∶DE=3∶8,解得DE= m.
16.解:(1)如图所示.
(2)根据俯视图和主视图可知a2+a2=h2=42,解得a=2.几何体的表面积为2ah+ah+a2×2=16+24.
17.解:由三视图可知,该工件为底面半径为10 cm,高为30 cm的圆锥体,这圆锥的母线长为=10(cm),圆锥的侧面积为s=πrl=×20π×10=100π(cm2),圆锥的底面积为102π=100π(cm2),圆锥的全面积为100π+100π=100(1+)π(cm2),圆锥的体积为×π×(20÷2)2×30=1000 π(cm3).故此工件的全面积是100(1+)π cm2,体积是1000π cm3.
18.解:(1)B
(2)10 图略.
19.解:根据题意,易证得△APD∽△A'PB,△PDE∽△PBP',∴==.又∵DE=CP'=1,AD=BC=3,将各线段长度代入得=,解得A'B=12,∴点A'到CD的距离为A'B+BC=12+3=15.
20.解:连接CD.由题易知∠B=90°,∠DOE=90°,点O,D,C共线.∵OD=0.8 m,OE=0.8 m,∴∠DEB=45°.∵∠B=90°,∴∠BAE=45°,∴AB=BE,设AB=EB=x m.∵∠B=∠DOE=90°,∴AB∥CO,∴△ABF∽△COF,∴=,即=,解得x=4.4.经检验x=4.4是原方程的解.答:围墙AB的高度是4.4 m.
21.解:(1)2+1.5(x-1)=(1.5x+0.5)m.
(2)由三视图可知共有12个碟子,∴叠成一摞后的高度为1.5×12+0.5=18.5(cm).
22.解:(1)如图所示,FM即为所求.
(2)设速度为x米/秒.根据题意得CG∥AH,∴△COG∽△AOH,∴=,即==.又∵CG∥AH,∴△EOG∽△MOH,∴=,即=,解得x=.答:小明沿AB方向匀速前进的速度为米/秒.
23.解:(1)该几何体中正方体的个数为9+4+1=14.
(2)如图所示.
(3)先算侧面:底层12个小面,中层8个,上层4个,再算上面:上层1个,中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,∴中层是3个),底层是9-4=5(个),总共有33个小面,∴涂上颜色部分的总面积是1×1×33=33(cm2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
