辽宁省沈阳市第二十中学2013届高三高考领航考试(三)数学(文)试题
文档属性
| 名称 | 辽宁省沈阳市第二十中学2013届高三高考领航考试(三)数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 717.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-17 00:00:00 | ||
图片预览




文档简介
沈阳市第二十中学2013届高考领航试卷(3)
出题人: 审题人:
一、选择题:
1.设集合,则满足的集合B的个数为( )
A.1 B.3 C.4 D.8
2.已知,其中是实数,是虚数单位,则( )
A. B. C. D.
3.已知,且,则( )
A. B. C. D.
4.设函数,则( )
A.在区间内均有零点
B.在区间内均无零点
C.在区间内有零点,在区间内无零点
D.在区间内无零点,在区间内有零点
5.实数满足,则的值为( )
A.8 B. C.0 D.10
6.设函数为定义在R上的奇函数,当时,(为常数),则( )
A.3 B.1 C. D.
7.如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数①;②;③;④ 其中“互为生成函数”的是( )
A.①② B.①③ C.③④ D.②④
8.在内,内角的对边分别是,若,,则A=( )
A. B. C. D.
9.已知是实数,则函数的图象不可能是( )
10.设命题非零向量是的充要条件;命题“”是“”的充要条件,则( )
A.为真命题 B.为假命题
C.为假命题 D.为真命题
11.已知二次函数,满足:对任意实数,都有,且当时,有成立,又,则为( )
A.1 B. C.2 D.0
12.若,且,则下面结论正确的是( )
A. B. C. D.
二、填空题:本大题共4个小题,每小题4分,共16分。(将答案填在答题纸上)
13.设曲线在点处的切线与直线平行,则 .
14.如果,那么= .
15.在中,,则 .
16.O是平面上一点,点是平面上不共线的三点。平面内的动点P满足,若,则·的值等于 .
三、解答题:
17.已知函数
(1)求函数的最小正周期和单调增区间;
(2)作出函数在一个周期内的图象。
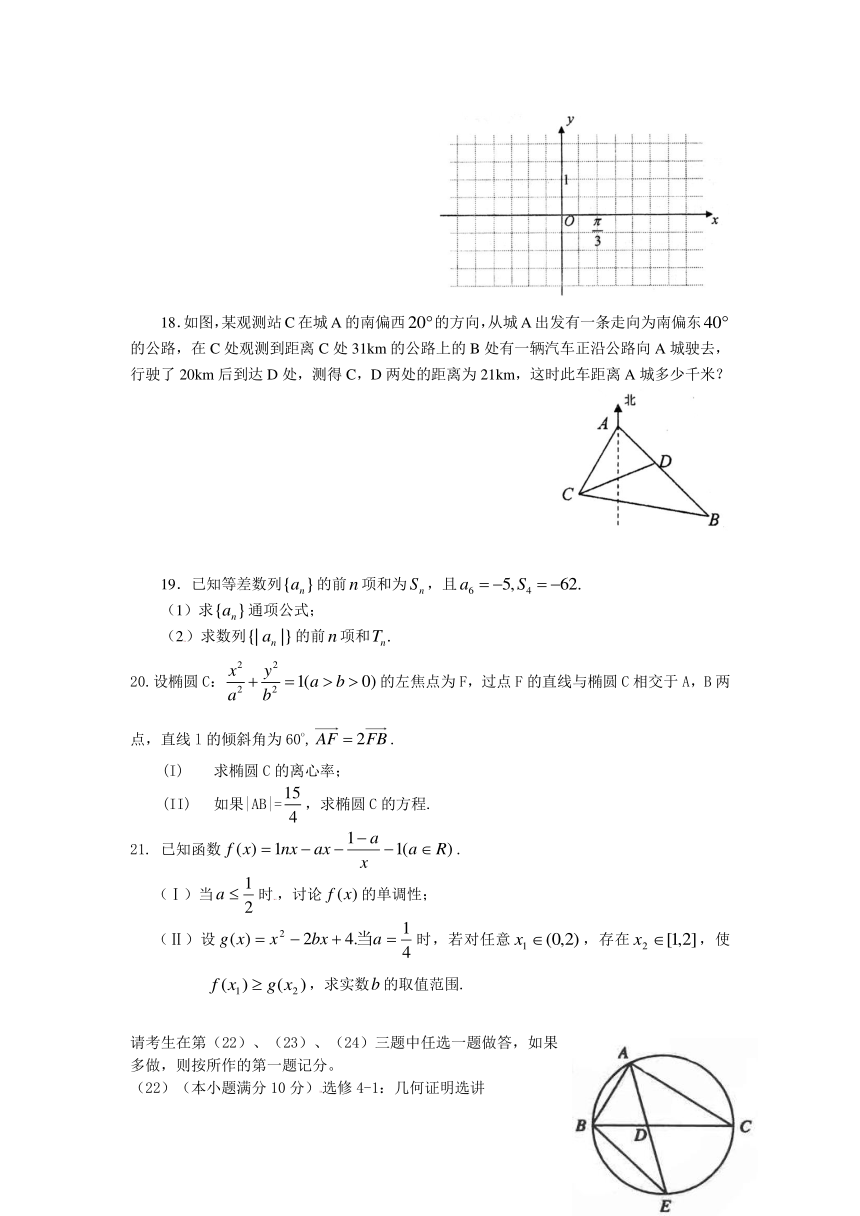
18.如图,某观测站C在城A的南偏西的方向,从城A出发有一条走向为南偏东的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
19.已知等差数列的前项和为,且
(1)求通项公式;
(2)求数列的前项和
20.设椭圆C:的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,.
求椭圆C的离心率;
如果|AB|=,求椭圆C的方程.
21. 已知函数.
(Ⅰ)当时,讨论的单调性;
(Ⅱ)设时,若对任意,存在,使,求实数的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所作的第一题记分。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,的角平分线AD的延长线交它的外接圆于点E
(I)证明:
(II)若的面积,求的大小。
(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知P为半圆C:(为参数,)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧的长度均为。
(I)以O为极点,轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(II)求直线AM的参数方程。
(24)(本小题满分10分)选修4-5:不等式选讲
已知均为正数,证明:,并确定为何值时,等号成立。
沈阳市第二十中学2013届高考领航试卷(文)
参 考 答 案
一、选择题
1.C 2.C 3.D 4.D 5.A 6.A 7.B 8.A
9.D 10.C 11.B 12.D
二、填空题
13.1 14. 15.3 16.0
三、解答题
17.解:(1)……2分
…………………………………………………………3分
∴最小正周期为 …………………………………………………………………4分
令,则,
所以函数的单调递增区间是…………………………6分
(2)列表
0
0
1
0
0
…………………………………………………………………………………………9分
画图略…………………………………………………………………………………12分
18.解:在中,,由余弦定理
,…………………3分
所以,…………………………………………5分
在中,由条件知,
所以………………8分
由正弦定理
所以 ………………………………………………………11分
故这时此车距离A城15千米……………………………………………………12分
19.解:(1)设等差数列的公差为,则由条件得
, ………………………………………………………………3分
解得, ………………………………………………………………5分
所以通项公式,则………………………6分
(2)令,则,
所以,当时,,当时,. ………………………………8分
所以,当时,
当时,
所以………………………………………………12分
(20)解:
设,由题意知<0,>0.
(Ⅰ)直线l的方程为 ,其中.
联立得
解得
因为,所以.
即
得离心率 . ……6分
(Ⅱ)因为,所以.
由得.所以,得a=3,.
椭圆C的方程为. ……12
(21)解:(Ⅰ)因为
所以
令
(1)当
所以,当,函数单调递减;
当时,,此时单调递
(2)当
即,解得
①当时,恒成立,
此时,函数在(0,+∞)上单调递减;
②当
时,单调递减;
时,单调递增;
,此时,函数单调递减;
③当时,由于
时,,此时,函数单调递减;
时,,此时,函数单调递增。
综上所述:
当时,函数在(0,1)上单调递减;
函数在(1,+∞)上单调递增;
当时,函数在(0,+∞)上单调递减;
当时,函数在(0, 1)上单调递减;
函数在上单调递增;
函数上单调递减,
(Ⅱ)因为,由(Ⅰ)知,
,当,
函数单调递减;当时,
函数单调递增,所以在(0,2)上的最小值为
由于“对任意,存在,使”等价于
“在[1,2]上的最小值不大于在(0,2)上的最小值” (*)
又,所以
①当时,因为,此时与(*)矛盾;
②当时,因为,同样与(*)矛盾;
③当时,因为
解不等式,可得
综上,的取值范围是
(22)证明:
(Ⅰ)由已知条件,可得
因为是同弧上的圆周角,所以
故△ABE∽△ADC. ……5分
(Ⅱ)因为△ABE∽△ADC,所以,即AB·AC=AD·AE.
又S=AB·ACsin,且S=AD·AE,故AB·ACsin= AD·AE.则sin=1,又为三角形内角,
所以=90°. ……10分
(23)解:
(Ⅰ)由已知,M点的极角为,且M点的极径等于,
故点M的极坐标为(,). ……5分
(Ⅱ)M点的直角坐标为(),A(0,1),故直线AM的参数方程为
(t为参数) ……10分
(24)证明:(证法一)
因为a,b,c均为正数,由平均值不等式得
①所以 ② ……6分
故.
又 ③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立。当且仅当时,③式等号成立。即当且仅当a=b=c=时,原式等号成立。 ……10分
(证法二)因为a,b,c均为正数,由基本不等式得
所以 ①
同理 ② ……6分
故
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,时,③式等号成立。
即当且仅当a=b=c=时,原式等号成立。 ……10分
沈阳市第二十中学2013届高考领航试卷(3)
出题人: 审题人:
一、选择题:
1.设集合,则满足的集合B的个数为( )
A.1 B.3 C.4 D.8
2.已知,其中是实数,是虚数单位,则( )
A. B. C. D.
3.已知,且,则( )
A. B. C. D.
4.设函数,则( )
A.在区间内均有零点
B.在区间内均无零点
C.在区间内有零点,在区间内无零点
D.在区间内无零点,在区间内有零点
5.实数满足,则的值为( )
A.8 B. C.0 D.10
6.设函数为定义在R上的奇函数,当时,(为常数),则( )
A.3 B.1 C. D.
7.如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数①;②;③;④ 其中“互为生成函数”的是( )
A.①② B.①③ C.③④ D.②④
8.在内,内角的对边分别是,若,,则A=( )
A. B. C. D.
9.已知是实数,则函数的图象不可能是( )
10.设命题非零向量是的充要条件;命题“”是“”的充要条件,则( )
A.为真命题 B.为假命题
C.为假命题 D.为真命题
11.已知二次函数,满足:对任意实数,都有,且当时,有成立,又,则为( )
A.1 B. C.2 D.0
12.若,且,则下面结论正确的是( )
A. B. C. D.
二、填空题:本大题共4个小题,每小题4分,共16分。(将答案填在答题纸上)
13.设曲线在点处的切线与直线平行,则 .
14.如果,那么= .
15.在中,,则 .
16.O是平面上一点,点是平面上不共线的三点。平面内的动点P满足,若,则·的值等于 .
三、解答题:
17.已知函数
(1)求函数的最小正周期和单调增区间;
(2)作出函数在一个周期内的图象。
18.如图,某观测站C在城A的南偏西的方向,从城A出发有一条走向为南偏东的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
19.已知等差数列的前项和为,且
(1)求通项公式;
(2)求数列的前项和
20.设椭圆C:的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,.
求椭圆C的离心率;
如果|AB|=,求椭圆C的方程.
21. 已知函数.
(Ⅰ)当时,讨论的单调性;
(Ⅱ)设时,若对任意,存在,使,求实数的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所作的第一题记分。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,的角平分线AD的延长线交它的外接圆于点E
(I)证明:
(II)若的面积,求的大小。
(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知P为半圆C:(为参数,)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧的长度均为。
(I)以O为极点,轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(II)求直线AM的参数方程。
(24)(本小题满分10分)选修4-5:不等式选讲
已知均为正数,证明:,并确定为何值时,等号成立。
沈阳市第二十中学2013届高考领航试卷(文)
参 考 答 案
一、选择题
1.C 2.C 3.D 4.D 5.A 6.A 7.B 8.A
9.D 10.C 11.B 12.D
二、填空题
13.1 14. 15.3 16.0
三、解答题
17.解:(1)……2分
…………………………………………………………3分
∴最小正周期为 …………………………………………………………………4分
令,则,
所以函数的单调递增区间是…………………………6分
(2)列表
0
0
1
0
0
…………………………………………………………………………………………9分
画图略…………………………………………………………………………………12分
18.解:在中,,由余弦定理
,…………………3分
所以,…………………………………………5分
在中,由条件知,
所以………………8分
由正弦定理
所以 ………………………………………………………11分
故这时此车距离A城15千米……………………………………………………12分
19.解:(1)设等差数列的公差为,则由条件得
, ………………………………………………………………3分
解得, ………………………………………………………………5分
所以通项公式,则………………………6分
(2)令,则,
所以,当时,,当时,. ………………………………8分
所以,当时,
当时,
所以………………………………………………12分
(20)解:
设,由题意知<0,>0.
(Ⅰ)直线l的方程为 ,其中.
联立得
解得
因为,所以.
即
得离心率 . ……6分
(Ⅱ)因为,所以.
由得.所以,得a=3,.
椭圆C的方程为. ……12
(21)解:(Ⅰ)因为
所以
令
(1)当
所以,当,函数单调递减;
当时,,此时单调递
(2)当
即,解得
①当时,恒成立,
此时,函数在(0,+∞)上单调递减;
②当
时,单调递减;
时,单调递增;
,此时,函数单调递减;
③当时,由于
时,,此时,函数单调递减;
时,,此时,函数单调递增。
综上所述:
当时,函数在(0,1)上单调递减;
函数在(1,+∞)上单调递增;
当时,函数在(0,+∞)上单调递减;
当时,函数在(0, 1)上单调递减;
函数在上单调递增;
函数上单调递减,
(Ⅱ)因为,由(Ⅰ)知,
,当,
函数单调递减;当时,
函数单调递增,所以在(0,2)上的最小值为
由于“对任意,存在,使”等价于
“在[1,2]上的最小值不大于在(0,2)上的最小值” (*)
又,所以
①当时,因为,此时与(*)矛盾;
②当时,因为,同样与(*)矛盾;
③当时,因为
解不等式,可得
综上,的取值范围是
(22)证明:
(Ⅰ)由已知条件,可得
因为是同弧上的圆周角,所以
故△ABE∽△ADC. ……5分
(Ⅱ)因为△ABE∽△ADC,所以,即AB·AC=AD·AE.
又S=AB·ACsin,且S=AD·AE,故AB·ACsin= AD·AE.则sin=1,又为三角形内角,
所以=90°. ……10分
(23)解:
(Ⅰ)由已知,M点的极角为,且M点的极径等于,
故点M的极坐标为(,). ……5分
(Ⅱ)M点的直角坐标为(),A(0,1),故直线AM的参数方程为
(t为参数) ……10分
(24)证明:(证法一)
因为a,b,c均为正数,由平均值不等式得
①所以 ② ……6分
故.
又 ③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立。当且仅当时,③式等号成立。即当且仅当a=b=c=时,原式等号成立。 ……10分
(证法二)因为a,b,c均为正数,由基本不等式得
所以 ①
同理 ② ……6分
故
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,时,③式等号成立。
即当且仅当a=b=c=时,原式等号成立。 ……10分
出题人: 审题人:
一、选择题:
1.设集合,则满足的集合B的个数为( )
A.1 B.3 C.4 D.8
2.已知,其中是实数,是虚数单位,则( )
A. B. C. D.
3.已知,且,则( )
A. B. C. D.
4.设函数,则( )
A.在区间内均有零点
B.在区间内均无零点
C.在区间内有零点,在区间内无零点
D.在区间内无零点,在区间内有零点
5.实数满足,则的值为( )
A.8 B. C.0 D.10
6.设函数为定义在R上的奇函数,当时,(为常数),则( )
A.3 B.1 C. D.
7.如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数①;②;③;④ 其中“互为生成函数”的是( )
A.①② B.①③ C.③④ D.②④
8.在内,内角的对边分别是,若,,则A=( )
A. B. C. D.
9.已知是实数,则函数的图象不可能是( )
10.设命题非零向量是的充要条件;命题“”是“”的充要条件,则( )
A.为真命题 B.为假命题
C.为假命题 D.为真命题
11.已知二次函数,满足:对任意实数,都有,且当时,有成立,又,则为( )
A.1 B. C.2 D.0
12.若,且,则下面结论正确的是( )
A. B. C. D.
二、填空题:本大题共4个小题,每小题4分,共16分。(将答案填在答题纸上)
13.设曲线在点处的切线与直线平行,则 .
14.如果,那么= .
15.在中,,则 .
16.O是平面上一点,点是平面上不共线的三点。平面内的动点P满足,若,则·的值等于 .
三、解答题:
17.已知函数
(1)求函数的最小正周期和单调增区间;
(2)作出函数在一个周期内的图象。
18.如图,某观测站C在城A的南偏西的方向,从城A出发有一条走向为南偏东的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
19.已知等差数列的前项和为,且
(1)求通项公式;
(2)求数列的前项和
20.设椭圆C:的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,.
求椭圆C的离心率;
如果|AB|=,求椭圆C的方程.
21. 已知函数.
(Ⅰ)当时,讨论的单调性;
(Ⅱ)设时,若对任意,存在,使,求实数的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所作的第一题记分。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,的角平分线AD的延长线交它的外接圆于点E
(I)证明:
(II)若的面积,求的大小。
(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知P为半圆C:(为参数,)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧的长度均为。
(I)以O为极点,轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(II)求直线AM的参数方程。
(24)(本小题满分10分)选修4-5:不等式选讲
已知均为正数,证明:,并确定为何值时,等号成立。
沈阳市第二十中学2013届高考领航试卷(文)
参 考 答 案
一、选择题
1.C 2.C 3.D 4.D 5.A 6.A 7.B 8.A
9.D 10.C 11.B 12.D
二、填空题
13.1 14. 15.3 16.0
三、解答题
17.解:(1)……2分
…………………………………………………………3分
∴最小正周期为 …………………………………………………………………4分
令,则,
所以函数的单调递增区间是…………………………6分
(2)列表
0
0
1
0
0
…………………………………………………………………………………………9分
画图略…………………………………………………………………………………12分
18.解:在中,,由余弦定理
,…………………3分
所以,…………………………………………5分
在中,由条件知,
所以………………8分
由正弦定理
所以 ………………………………………………………11分
故这时此车距离A城15千米……………………………………………………12分
19.解:(1)设等差数列的公差为,则由条件得
, ………………………………………………………………3分
解得, ………………………………………………………………5分
所以通项公式,则………………………6分
(2)令,则,
所以,当时,,当时,. ………………………………8分
所以,当时,
当时,
所以………………………………………………12分
(20)解:
设,由题意知<0,>0.
(Ⅰ)直线l的方程为 ,其中.
联立得
解得
因为,所以.
即
得离心率 . ……6分
(Ⅱ)因为,所以.
由得.所以,得a=3,.
椭圆C的方程为. ……12
(21)解:(Ⅰ)因为
所以
令
(1)当
所以,当,函数单调递减;
当时,,此时单调递
(2)当
即,解得
①当时,恒成立,
此时,函数在(0,+∞)上单调递减;
②当
时,单调递减;
时,单调递增;
,此时,函数单调递减;
③当时,由于
时,,此时,函数单调递减;
时,,此时,函数单调递增。
综上所述:
当时,函数在(0,1)上单调递减;
函数在(1,+∞)上单调递增;
当时,函数在(0,+∞)上单调递减;
当时,函数在(0, 1)上单调递减;
函数在上单调递增;
函数上单调递减,
(Ⅱ)因为,由(Ⅰ)知,
,当,
函数单调递减;当时,
函数单调递增,所以在(0,2)上的最小值为
由于“对任意,存在,使”等价于
“在[1,2]上的最小值不大于在(0,2)上的最小值” (*)
又,所以
①当时,因为,此时与(*)矛盾;
②当时,因为,同样与(*)矛盾;
③当时,因为
解不等式,可得
综上,的取值范围是
(22)证明:
(Ⅰ)由已知条件,可得
因为是同弧上的圆周角,所以
故△ABE∽△ADC. ……5分
(Ⅱ)因为△ABE∽△ADC,所以,即AB·AC=AD·AE.
又S=AB·ACsin,且S=AD·AE,故AB·ACsin= AD·AE.则sin=1,又为三角形内角,
所以=90°. ……10分
(23)解:
(Ⅰ)由已知,M点的极角为,且M点的极径等于,
故点M的极坐标为(,). ……5分
(Ⅱ)M点的直角坐标为(),A(0,1),故直线AM的参数方程为
(t为参数) ……10分
(24)证明:(证法一)
因为a,b,c均为正数,由平均值不等式得
①所以 ② ……6分
故.
又 ③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立。当且仅当时,③式等号成立。即当且仅当a=b=c=时,原式等号成立。 ……10分
(证法二)因为a,b,c均为正数,由基本不等式得
所以 ①
同理 ② ……6分
故
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,时,③式等号成立。
即当且仅当a=b=c=时,原式等号成立。 ……10分
沈阳市第二十中学2013届高考领航试卷(3)
出题人: 审题人:
一、选择题:
1.设集合,则满足的集合B的个数为( )
A.1 B.3 C.4 D.8
2.已知,其中是实数,是虚数单位,则( )
A. B. C. D.
3.已知,且,则( )
A. B. C. D.
4.设函数,则( )
A.在区间内均有零点
B.在区间内均无零点
C.在区间内有零点,在区间内无零点
D.在区间内无零点,在区间内有零点
5.实数满足,则的值为( )
A.8 B. C.0 D.10
6.设函数为定义在R上的奇函数,当时,(为常数),则( )
A.3 B.1 C. D.
7.如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数①;②;③;④ 其中“互为生成函数”的是( )
A.①② B.①③ C.③④ D.②④
8.在内,内角的对边分别是,若,,则A=( )
A. B. C. D.
9.已知是实数,则函数的图象不可能是( )
10.设命题非零向量是的充要条件;命题“”是“”的充要条件,则( )
A.为真命题 B.为假命题
C.为假命题 D.为真命题
11.已知二次函数,满足:对任意实数,都有,且当时,有成立,又,则为( )
A.1 B. C.2 D.0
12.若,且,则下面结论正确的是( )
A. B. C. D.
二、填空题:本大题共4个小题,每小题4分,共16分。(将答案填在答题纸上)
13.设曲线在点处的切线与直线平行,则 .
14.如果,那么= .
15.在中,,则 .
16.O是平面上一点,点是平面上不共线的三点。平面内的动点P满足,若,则·的值等于 .
三、解答题:
17.已知函数
(1)求函数的最小正周期和单调增区间;
(2)作出函数在一个周期内的图象。
18.如图,某观测站C在城A的南偏西的方向,从城A出发有一条走向为南偏东的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
19.已知等差数列的前项和为,且
(1)求通项公式;
(2)求数列的前项和
20.设椭圆C:的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,.
求椭圆C的离心率;
如果|AB|=,求椭圆C的方程.
21. 已知函数.
(Ⅰ)当时,讨论的单调性;
(Ⅱ)设时,若对任意,存在,使,求实数的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所作的第一题记分。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,的角平分线AD的延长线交它的外接圆于点E
(I)证明:
(II)若的面积,求的大小。
(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知P为半圆C:(为参数,)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧的长度均为。
(I)以O为极点,轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(II)求直线AM的参数方程。
(24)(本小题满分10分)选修4-5:不等式选讲
已知均为正数,证明:,并确定为何值时,等号成立。
沈阳市第二十中学2013届高考领航试卷(文)
参 考 答 案
一、选择题
1.C 2.C 3.D 4.D 5.A 6.A 7.B 8.A
9.D 10.C 11.B 12.D
二、填空题
13.1 14. 15.3 16.0
三、解答题
17.解:(1)……2分
…………………………………………………………3分
∴最小正周期为 …………………………………………………………………4分
令,则,
所以函数的单调递增区间是…………………………6分
(2)列表
0
0
1
0
0
…………………………………………………………………………………………9分
画图略…………………………………………………………………………………12分
18.解:在中,,由余弦定理
,…………………3分
所以,…………………………………………5分
在中,由条件知,
所以………………8分
由正弦定理
所以 ………………………………………………………11分
故这时此车距离A城15千米……………………………………………………12分
19.解:(1)设等差数列的公差为,则由条件得
, ………………………………………………………………3分
解得, ………………………………………………………………5分
所以通项公式,则………………………6分
(2)令,则,
所以,当时,,当时,. ………………………………8分
所以,当时,
当时,
所以………………………………………………12分
(20)解:
设,由题意知<0,>0.
(Ⅰ)直线l的方程为 ,其中.
联立得
解得
因为,所以.
即
得离心率 . ……6分
(Ⅱ)因为,所以.
由得.所以,得a=3,.
椭圆C的方程为. ……12
(21)解:(Ⅰ)因为
所以
令
(1)当
所以,当,函数单调递减;
当时,,此时单调递
(2)当
即,解得
①当时,恒成立,
此时,函数在(0,+∞)上单调递减;
②当
时,单调递减;
时,单调递增;
,此时,函数单调递减;
③当时,由于
时,,此时,函数单调递减;
时,,此时,函数单调递增。
综上所述:
当时,函数在(0,1)上单调递减;
函数在(1,+∞)上单调递增;
当时,函数在(0,+∞)上单调递减;
当时,函数在(0, 1)上单调递减;
函数在上单调递增;
函数上单调递减,
(Ⅱ)因为,由(Ⅰ)知,
,当,
函数单调递减;当时,
函数单调递增,所以在(0,2)上的最小值为
由于“对任意,存在,使”等价于
“在[1,2]上的最小值不大于在(0,2)上的最小值” (*)
又,所以
①当时,因为,此时与(*)矛盾;
②当时,因为,同样与(*)矛盾;
③当时,因为
解不等式,可得
综上,的取值范围是
(22)证明:
(Ⅰ)由已知条件,可得
因为是同弧上的圆周角,所以
故△ABE∽△ADC. ……5分
(Ⅱ)因为△ABE∽△ADC,所以,即AB·AC=AD·AE.
又S=AB·ACsin,且S=AD·AE,故AB·ACsin= AD·AE.则sin=1,又为三角形内角,
所以=90°. ……10分
(23)解:
(Ⅰ)由已知,M点的极角为,且M点的极径等于,
故点M的极坐标为(,). ……5分
(Ⅱ)M点的直角坐标为(),A(0,1),故直线AM的参数方程为
(t为参数) ……10分
(24)证明:(证法一)
因为a,b,c均为正数,由平均值不等式得
①所以 ② ……6分
故.
又 ③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立。当且仅当时,③式等号成立。即当且仅当a=b=c=时,原式等号成立。 ……10分
(证法二)因为a,b,c均为正数,由基本不等式得
所以 ①
同理 ② ……6分
故
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,时,③式等号成立。
即当且仅当a=b=c=时,原式等号成立。 ……10分
同课章节目录
