北师大版九年级数学《圆》单元测试一 有答案
文档属性
| 名称 | 北师大版九年级数学《圆》单元测试一 有答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 441.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-17 00:00:00 | ||
图片预览



文档简介
北师大版九年级数学《圆》单元测试一
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,C是⊙O上一点,O是圆心.若∠AOB=80°,则∠ACB的度数为( )
A、800 B、1000 C、1600 D、400
2.下列命题中,正确的是( )
A.任意三点确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.垂直弦的直线必过圆心
3.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m,母线长为3m,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是( )
A. B. C. D.
4.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
5.如图,一块三角形绿化园地,三个角都做有半径为R的圆形喷水池,则这三个喷水池占去的绿化园地(即阴影部分)的面积为
A. B. C. D. 不能确定
6.扇形的圆心角是600 ,则扇形的面积是所在圆面积的( )
A. B. C. D.
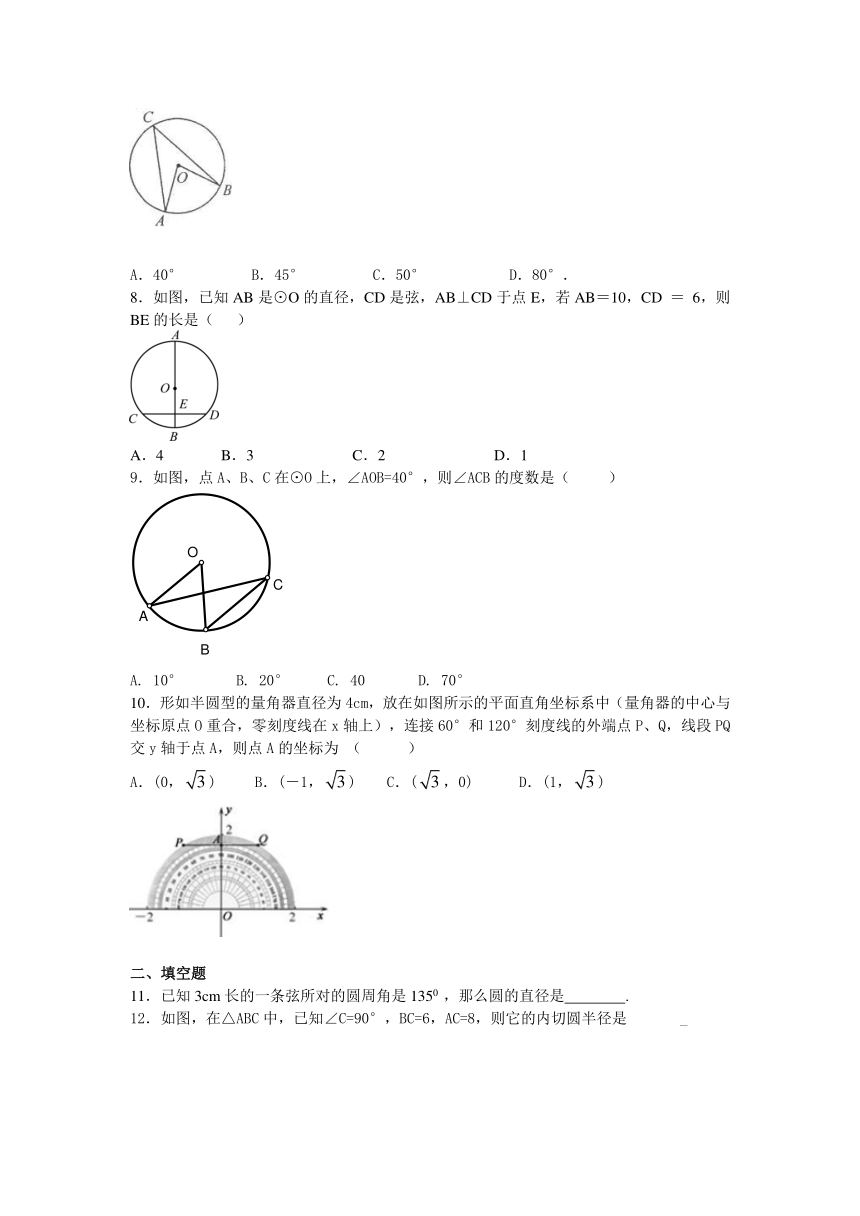
7.如图,∠AOB是⊙O的圆心角,∠AOB=90°,则弧所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°.
8.如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD = 6,则BE的长是( )
A.4 B.3 C.2 D.1
9.如图,点A、B、C在⊙O上,∠AOB=40°,则∠ACB的度数是( )
A. 10° B. 20° C. 40 D. 70°
10.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的外端点P、Q,线段PQ交y轴于点A,则点A的坐标为 ( )
A.(0,) B.(-1,) C.(,0) D.(1,)
二、填空题
11.已知3cm长的一条弦所对的圆周角是1350 ,那么圆的直径是 .
12.如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是 _
13.如图,PA、PB、DE分别切⊙O于A、B、C,如果ΔPDE的周长为8,那么PA=_______
14.如图,AD是△ABC的外接圆直径,AD=,∠B=∠DAC,则AC的值为 .
15.圆锥的底面半径为3cm,母线长为4cm,那么这个圆锥的侧面积是 cm2.
16.若圆锥的底面周长为3π,侧面展开后所得扇形的圆心角为180°,则圆锥的侧面积为 .
三、计算题
17.
又PE⊥CB于E,若BC=10,且CE∶EB=3∶2,求AB的长.
18.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
四、解答题
19.(本题6分)如图(第18题①),是日全食的初亏阶段,请用直尺和圆规作图,把图(第18题②)中的太阳补充完整.不写作法,但保留作图痕迹.
20.如图,扇形OAB的圆心角为120°,半径为6cm.⑴请用尺规作出扇形的对称轴(不写做法,保留作图痕迹).⑵若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面积.
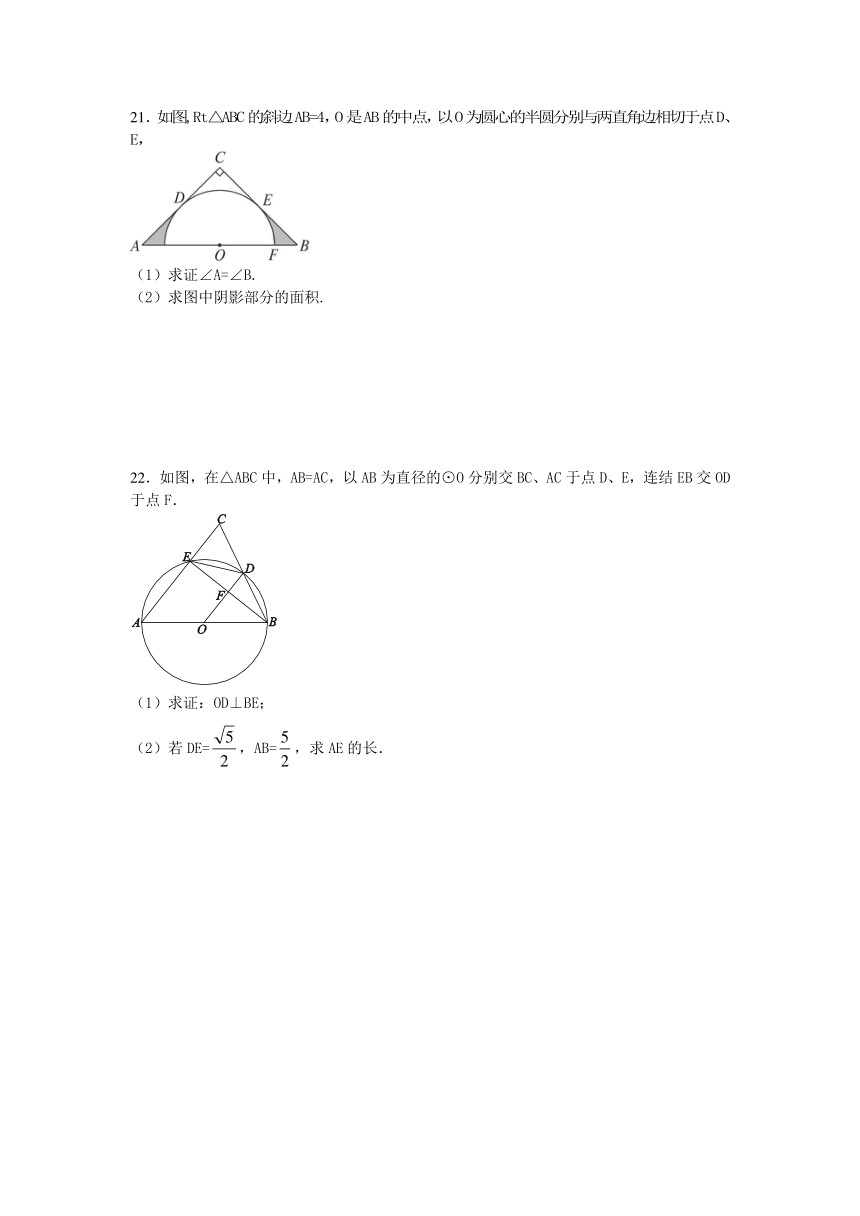
21.如图,Rt△ABC的斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两直角边相切于点D、E,
(1)求证∠A=∠B.
(2)求图中阴影部分的面积.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,连结EB交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=,求AE的长.
23.如图,在⊙O中,∠ACB=∠BDC=60°,AC=,
(1)判断△ABC的形状并证明你的结论;
(2)求⊙O的周长
24.如图,在等边△ABC中,AD⊥BC于点D,一个直径与AD相等的圆与BC相切于点E,与AB相切于点F,连接EF。
(1)判断EF与AC的位置关系(不必说明理由);;
(2)如图(2),过E作BC的垂线,交圆于G,连接AG,判断四边形ADEG的形状,并说明理由。
(3)求证:AC与GE的交点O为此圆的圆心.
25.如图,点A、B、D、在⊙O上,弦AE、BD的延长线相交于点C.。若AB是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,△ABC还需满足什么条件,点E才一定是AC的中点?(直接写出结论)
26.已知OA、OB是⊙O的两条半径,且OA⊥BC,C为OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD,交OC过于点E。
(1)求证:CD=CE;
(2)若将图1中的半径OB所在的直线向上平行移动,交⊙O于,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
参考答案
1.D
2.C
3.B
4.B
5.B
6.B
7.B
8.D
9.B
10.A
11.
12.2
13.4
14. 1
15. 15π
16.
17.
∴CD⊥AB
又∵BC=10
CE∶EB=3∶2
∴EC=6,BE=4
又∵PE⊥BC
∴Rt△BEP∽Rt△BPC
18.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
19.略
20.(1)略(2)
21.2-
22
.
23.(1)
24.(1)EF∥AC;(2)四边形ADEG为矩形。
25.(1)AB=AC;(2)△ABC为正三角形,或AB=BC,或AC=BC,或∠A=∠B,或∠A=∠C.
26.
北师大版九年级数学《圆》单元测试一
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,C是⊙O上一点,O是圆心.若∠AOB=80°,则∠ACB的度数为( )
A、800 B、1000 C、1600 D、400
2.下列命题中,正确的是( )
A.任意三点确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.垂直弦的直线必过圆心
3.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m,母线长为3m,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是( )
A. B. C. D.
4.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
5.如图,一块三角形绿化园地,三个角都做有半径为R的圆形喷水池,则这三个喷水池占去的绿化园地(即阴影部分)的面积为
A. B. C. D. 不能确定
6.扇形的圆心角是600 ,则扇形的面积是所在圆面积的( )
A. B. C. D.
7.如图,∠AOB是⊙O的圆心角,∠AOB=90°,则弧所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°.
8.如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD = 6,则BE的长是( )
A.4 B.3 C.2 D.1
9.如图,点A、B、C在⊙O上,∠AOB=40°,则∠ACB的度数是( )
A. 10° B. 20° C. 40 D. 70°
10.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的外端点P、Q,线段PQ交y轴于点A,则点A的坐标为 ( )
A.(0,) B.(-1,) C.(,0) D.(1,)
二、填空题
11.已知3cm长的一条弦所对的圆周角是1350 ,那么圆的直径是 .
12.如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是 _
13.如图,PA、PB、DE分别切⊙O于A、B、C,如果ΔPDE的周长为8,那么PA=_______
14.如图,AD是△ABC的外接圆直径,AD=,∠B=∠DAC,则AC的值为 .
15.圆锥的底面半径为3cm,母线长为4cm,那么这个圆锥的侧面积是 cm2.
16.若圆锥的底面周长为3π,侧面展开后所得扇形的圆心角为180°,则圆锥的侧面积为 .
三、计算题
17.
又PE⊥CB于E,若BC=10,且CE∶EB=3∶2,求AB的长.
18.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
四、解答题
19.(本题6分)如图(第18题①),是日全食的初亏阶段,请用直尺和圆规作图,把图(第18题②)中的太阳补充完整.不写作法,但保留作图痕迹.
20.如图,扇形OAB的圆心角为120°,半径为6cm.⑴请用尺规作出扇形的对称轴(不写做法,保留作图痕迹).⑵若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面积.
21.如图,Rt△ABC的斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两直角边相切于点D、E,
(1)求证∠A=∠B.
(2)求图中阴影部分的面积.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,连结EB交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=,求AE的长.
23.如图,在⊙O中,∠ACB=∠BDC=60°,AC=,
(1)判断△ABC的形状并证明你的结论;
(2)求⊙O的周长
24.如图,在等边△ABC中,AD⊥BC于点D,一个直径与AD相等的圆与BC相切于点E,与AB相切于点F,连接EF。
(1)判断EF与AC的位置关系(不必说明理由);;
(2)如图(2),过E作BC的垂线,交圆于G,连接AG,判断四边形ADEG的形状,并说明理由。
(3)求证:AC与GE的交点O为此圆的圆心.
25.如图,点A、B、D、在⊙O上,弦AE、BD的延长线相交于点C.。若AB是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,△ABC还需满足什么条件,点E才一定是AC的中点?(直接写出结论)
26.已知OA、OB是⊙O的两条半径,且OA⊥BC,C为OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD,交OC过于点E。
(1)求证:CD=CE;
(2)若将图1中的半径OB所在的直线向上平行移动,交⊙O于,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
参考答案
1.D
2.C
3.B
4.B
5.B
6.B
7.B
8.D
9.B
10.A
11.
12.2
13.4
14. 1
15. 15π
16.
17.
∴CD⊥AB
又∵BC=10
CE∶EB=3∶2
∴EC=6,BE=4
又∵PE⊥BC
∴Rt△BEP∽Rt△BPC
18.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
19.略
20.(1)略(2)
21.2-
22
.
23.(1)
24.(1)EF∥AC;(2)四边形ADEG为矩形。
25.(1)AB=AC;(2)△ABC为正三角形,或AB=BC,或AC=BC,或∠A=∠B,或∠A=∠C.
26.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,C是⊙O上一点,O是圆心.若∠AOB=80°,则∠ACB的度数为( )
A、800 B、1000 C、1600 D、400
2.下列命题中,正确的是( )
A.任意三点确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.垂直弦的直线必过圆心
3.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m,母线长为3m,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是( )
A. B. C. D.
4.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
5.如图,一块三角形绿化园地,三个角都做有半径为R的圆形喷水池,则这三个喷水池占去的绿化园地(即阴影部分)的面积为
A. B. C. D. 不能确定
6.扇形的圆心角是600 ,则扇形的面积是所在圆面积的( )
A. B. C. D.
7.如图,∠AOB是⊙O的圆心角,∠AOB=90°,则弧所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°.
8.如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD = 6,则BE的长是( )
A.4 B.3 C.2 D.1
9.如图,点A、B、C在⊙O上,∠AOB=40°,则∠ACB的度数是( )
A. 10° B. 20° C. 40 D. 70°
10.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的外端点P、Q,线段PQ交y轴于点A,则点A的坐标为 ( )
A.(0,) B.(-1,) C.(,0) D.(1,)
二、填空题
11.已知3cm长的一条弦所对的圆周角是1350 ,那么圆的直径是 .
12.如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是 _
13.如图,PA、PB、DE分别切⊙O于A、B、C,如果ΔPDE的周长为8,那么PA=_______
14.如图,AD是△ABC的外接圆直径,AD=,∠B=∠DAC,则AC的值为 .
15.圆锥的底面半径为3cm,母线长为4cm,那么这个圆锥的侧面积是 cm2.
16.若圆锥的底面周长为3π,侧面展开后所得扇形的圆心角为180°,则圆锥的侧面积为 .
三、计算题
17.
又PE⊥CB于E,若BC=10,且CE∶EB=3∶2,求AB的长.
18.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
四、解答题
19.(本题6分)如图(第18题①),是日全食的初亏阶段,请用直尺和圆规作图,把图(第18题②)中的太阳补充完整.不写作法,但保留作图痕迹.
20.如图,扇形OAB的圆心角为120°,半径为6cm.⑴请用尺规作出扇形的对称轴(不写做法,保留作图痕迹).⑵若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面积.
21.如图,Rt△ABC的斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两直角边相切于点D、E,
(1)求证∠A=∠B.
(2)求图中阴影部分的面积.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,连结EB交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=,求AE的长.
23.如图,在⊙O中,∠ACB=∠BDC=60°,AC=,
(1)判断△ABC的形状并证明你的结论;
(2)求⊙O的周长
24.如图,在等边△ABC中,AD⊥BC于点D,一个直径与AD相等的圆与BC相切于点E,与AB相切于点F,连接EF。
(1)判断EF与AC的位置关系(不必说明理由);;
(2)如图(2),过E作BC的垂线,交圆于G,连接AG,判断四边形ADEG的形状,并说明理由。
(3)求证:AC与GE的交点O为此圆的圆心.
25.如图,点A、B、D、在⊙O上,弦AE、BD的延长线相交于点C.。若AB是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,△ABC还需满足什么条件,点E才一定是AC的中点?(直接写出结论)
26.已知OA、OB是⊙O的两条半径,且OA⊥BC,C为OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD,交OC过于点E。
(1)求证:CD=CE;
(2)若将图1中的半径OB所在的直线向上平行移动,交⊙O于,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
参考答案
1.D
2.C
3.B
4.B
5.B
6.B
7.B
8.D
9.B
10.A
11.
12.2
13.4
14. 1
15. 15π
16.
17.
∴CD⊥AB
又∵BC=10
CE∶EB=3∶2
∴EC=6,BE=4
又∵PE⊥BC
∴Rt△BEP∽Rt△BPC
18.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
19.略
20.(1)略(2)
21.2-
22
.
23.(1)
24.(1)EF∥AC;(2)四边形ADEG为矩形。
25.(1)AB=AC;(2)△ABC为正三角形,或AB=BC,或AC=BC,或∠A=∠B,或∠A=∠C.
26.
北师大版九年级数学《圆》单元测试一
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,C是⊙O上一点,O是圆心.若∠AOB=80°,则∠ACB的度数为( )
A、800 B、1000 C、1600 D、400
2.下列命题中,正确的是( )
A.任意三点确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.垂直弦的直线必过圆心
3.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m,母线长为3m,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是( )
A. B. C. D.
4.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
5.如图,一块三角形绿化园地,三个角都做有半径为R的圆形喷水池,则这三个喷水池占去的绿化园地(即阴影部分)的面积为
A. B. C. D. 不能确定
6.扇形的圆心角是600 ,则扇形的面积是所在圆面积的( )
A. B. C. D.
7.如图,∠AOB是⊙O的圆心角,∠AOB=90°,则弧所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°.
8.如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD = 6,则BE的长是( )
A.4 B.3 C.2 D.1
9.如图,点A、B、C在⊙O上,∠AOB=40°,则∠ACB的度数是( )
A. 10° B. 20° C. 40 D. 70°
10.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的外端点P、Q,线段PQ交y轴于点A,则点A的坐标为 ( )
A.(0,) B.(-1,) C.(,0) D.(1,)
二、填空题
11.已知3cm长的一条弦所对的圆周角是1350 ,那么圆的直径是 .
12.如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是 _
13.如图,PA、PB、DE分别切⊙O于A、B、C,如果ΔPDE的周长为8,那么PA=_______
14.如图,AD是△ABC的外接圆直径,AD=,∠B=∠DAC,则AC的值为 .
15.圆锥的底面半径为3cm,母线长为4cm,那么这个圆锥的侧面积是 cm2.
16.若圆锥的底面周长为3π,侧面展开后所得扇形的圆心角为180°,则圆锥的侧面积为 .
三、计算题
17.
又PE⊥CB于E,若BC=10,且CE∶EB=3∶2,求AB的长.
18.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
四、解答题
19.(本题6分)如图(第18题①),是日全食的初亏阶段,请用直尺和圆规作图,把图(第18题②)中的太阳补充完整.不写作法,但保留作图痕迹.
20.如图,扇形OAB的圆心角为120°,半径为6cm.⑴请用尺规作出扇形的对称轴(不写做法,保留作图痕迹).⑵若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面积.
21.如图,Rt△ABC的斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两直角边相切于点D、E,
(1)求证∠A=∠B.
(2)求图中阴影部分的面积.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,连结EB交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=,求AE的长.
23.如图,在⊙O中,∠ACB=∠BDC=60°,AC=,
(1)判断△ABC的形状并证明你的结论;
(2)求⊙O的周长
24.如图,在等边△ABC中,AD⊥BC于点D,一个直径与AD相等的圆与BC相切于点E,与AB相切于点F,连接EF。
(1)判断EF与AC的位置关系(不必说明理由);;
(2)如图(2),过E作BC的垂线,交圆于G,连接AG,判断四边形ADEG的形状,并说明理由。
(3)求证:AC与GE的交点O为此圆的圆心.
25.如图,点A、B、D、在⊙O上,弦AE、BD的延长线相交于点C.。若AB是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,△ABC还需满足什么条件,点E才一定是AC的中点?(直接写出结论)
26.已知OA、OB是⊙O的两条半径,且OA⊥BC,C为OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD,交OC过于点E。
(1)求证:CD=CE;
(2)若将图1中的半径OB所在的直线向上平行移动,交⊙O于,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
参考答案
1.D
2.C
3.B
4.B
5.B
6.B
7.B
8.D
9.B
10.A
11.
12.2
13.4
14. 1
15. 15π
16.
17.
∴CD⊥AB
又∵BC=10
CE∶EB=3∶2
∴EC=6,BE=4
又∵PE⊥BC
∴Rt△BEP∽Rt△BPC
18.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
19.略
20.(1)略(2)
21.2-
22
.
23.(1)
24.(1)EF∥AC;(2)四边形ADEG为矩形。
25.(1)AB=AC;(2)△ABC为正三角形,或AB=BC,或AC=BC,或∠A=∠B,或∠A=∠C.
26.
