4.2全反射同步练习(word版含答案)
文档属性
| 名称 | 4.2全反射同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-30 06:18:29 | ||
图片预览



文档简介
人教版(2019)选择性必修一 4.2 全反射 同步练习
一、单选题
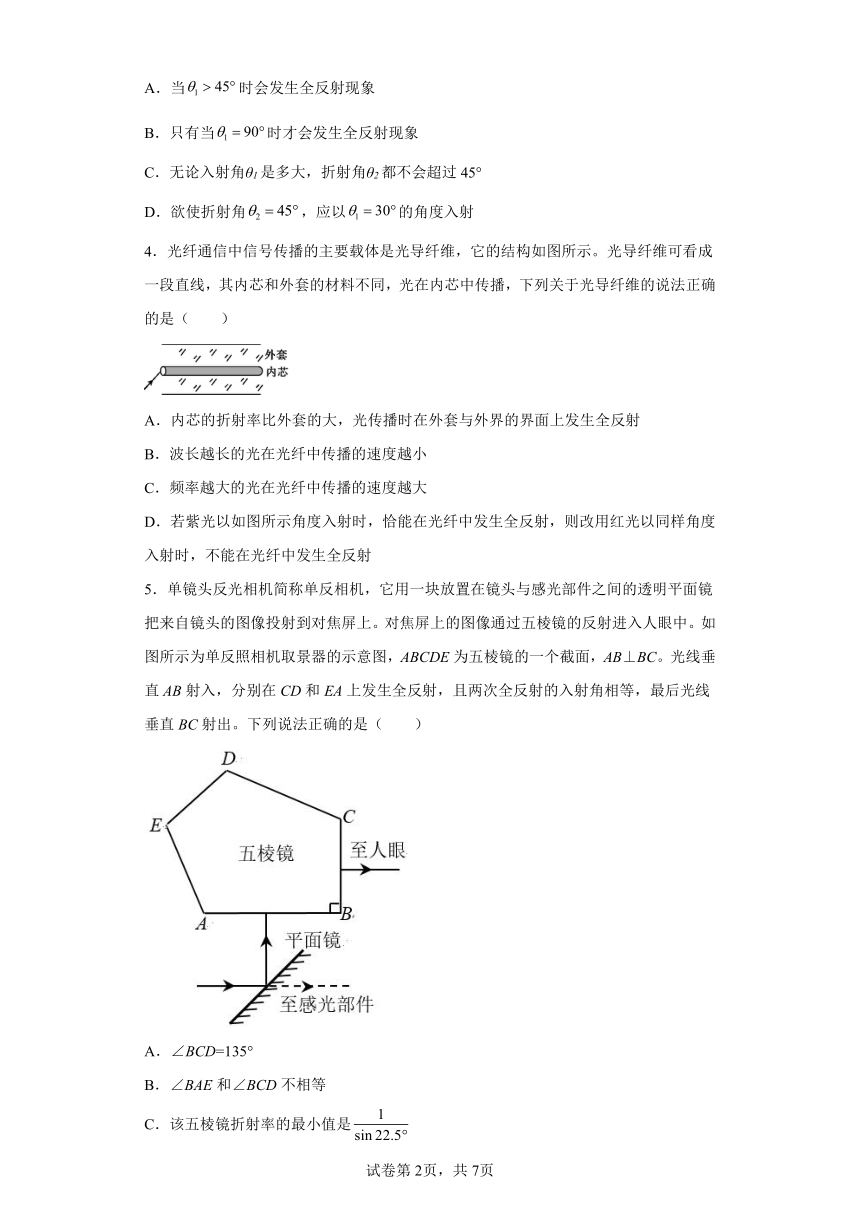
1.如图所示,一透明半圆柱体折射率为n = 2,半径为 R、长为 L。一平行光束从半圆柱体的矩形表面垂直射入,有光线从部分柱面射出。则该部分柱面的面积为( )
A. B. C. D.
2.如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合。一束白光沿着半圆柱形玻璃砖的半径从圆弧面垂直BD射到圆心O点上。使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动。在玻璃砖转动过程中,以下说法正确的是( )
A.在弧形屏上可以观察到反射光的色散现象
B.红光在玻璃砖中传播速度最小
C.折射光斑在弧形屏上沿顺时针方向移动
D.玻璃砖旋转过程中弧形屏上最先消失的一定是红光
3.如图所示,一束光从空气中射向折射率为的某种玻璃的表面,θ1表示入射角,则下列说法正确的是( )
A.当时会发生全反射现象
B.只有当时才会发生全反射现象
C.无论入射角θ1是多大,折射角θ2都不会超过45°
D.欲使折射角,应以的角度入射
4.光纤通信中信号传播的主要载体是光导纤维,它的结构如图所示。光导纤维可看成一段直线,其内芯和外套的材料不同,光在内芯中传播,下列关于光导纤维的说法正确的是( )
A.内芯的折射率比外套的大,光传播时在外套与外界的界面上发生全反射
B.波长越长的光在光纤中传播的速度越小
C.频率越大的光在光纤中传播的速度越大
D.若紫光以如图所示角度入射时,恰能在光纤中发生全反射,则改用红光以同样角度入射时,不能在光纤中发生全反射
5.单镜头反光相机简称单反相机,它用一块放置在镜头与感光部件之间的透明平面镜把来自镜头的图像投射到对焦屏上。对焦屏上的图像通过五棱镜的反射进入人眼中。如图所示为单反照相机取景器的示意图,ABCDE为五棱镜的一个截面,AB⊥BC。光线垂直AB射入,分别在CD和EA上发生全反射,且两次全反射的入射角相等,最后光线垂直BC射出。下列说法正确的是( )
A.∠BCD=135°
B.∠BAE和∠BCD不相等
C.该五棱镜折射率的最小值是
D.该五棱镜折射率的最小值是
6.如图所示,扇形AOB为透明柱状介质的横截面,圆心角∠AOB=60°。一束平行于角平分线OM的单色光由OA射入介质,经OA折射的光线恰平行于OB,以下对介质的折射率值及折射光线中恰好射到M点的光线能不能发生全反射的说法正确的是( )
A.,不能发生全反射 B.,能发生全反射
C.,不能发生全反射 D.,能发生全反射
7.如图所示,一光导纤维内芯的折射率为n1,外套的折射率为n2,一束光信号与界面夹角为α由内芯射向外套,要在界面发生全反射,必须满足的条件是 ( )
A.n1>n2,α小于某一值 B.n1C.n1>n2,α大于某一值 D.n18.一束单色光从空气进入水中,下列说法正确的是( )
A.光的频率不变
B.光的传播速度变大
C.折射角大于入射角
D.入射角增大到某一角度时将会发生全反射
9.打磨某剖面如图所示的宝石时,必须将OP、OQ边与轴线的夹角θ切磨在θ1<θ<θ2的范围内,才能使从MN边垂直入射的光线,在OP边和OQ边都发生全反射(仅考虑如图所示的光线第一次射到OP边并反射到OQ边后射向MN边的情况),则下列判断正确的是( )
A.若θ>θ2,光线一定在OP边发生全反射
B.若θ>θ2,光线会从OQ边射出
C.若θ>θ1,光线会从OP边射出
D.若θ<θ1,光线会在OP边发生全反射
10.一束包含各频率成分的激光同时进入光导纤维传播,下列说法正确的是( )
A.传播激光信号的光导纤维内芯折射率比外套的低
B.各频率成分的激光束通过光导纤维后频率会降低
C.各频率成分的激光束在光导纤维传播过程中前端部分频率更高
D.各频率成分的激光束在光导纤维传播过程中前端部分波长更长
11.在桌面上有一倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示。有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为1.5,则光束在桌面上形成的光斑半径为( )
A.0.5r B.r C.1.5r D.2.0r
12.如图所示,平静的湖面上漂浮着一圆形荷叶,O为荷叶圆心,O点的正下方A处有一条小鱼(可视为质点),已知O到A的距离,荷叶的半径,水的折射率,则( )
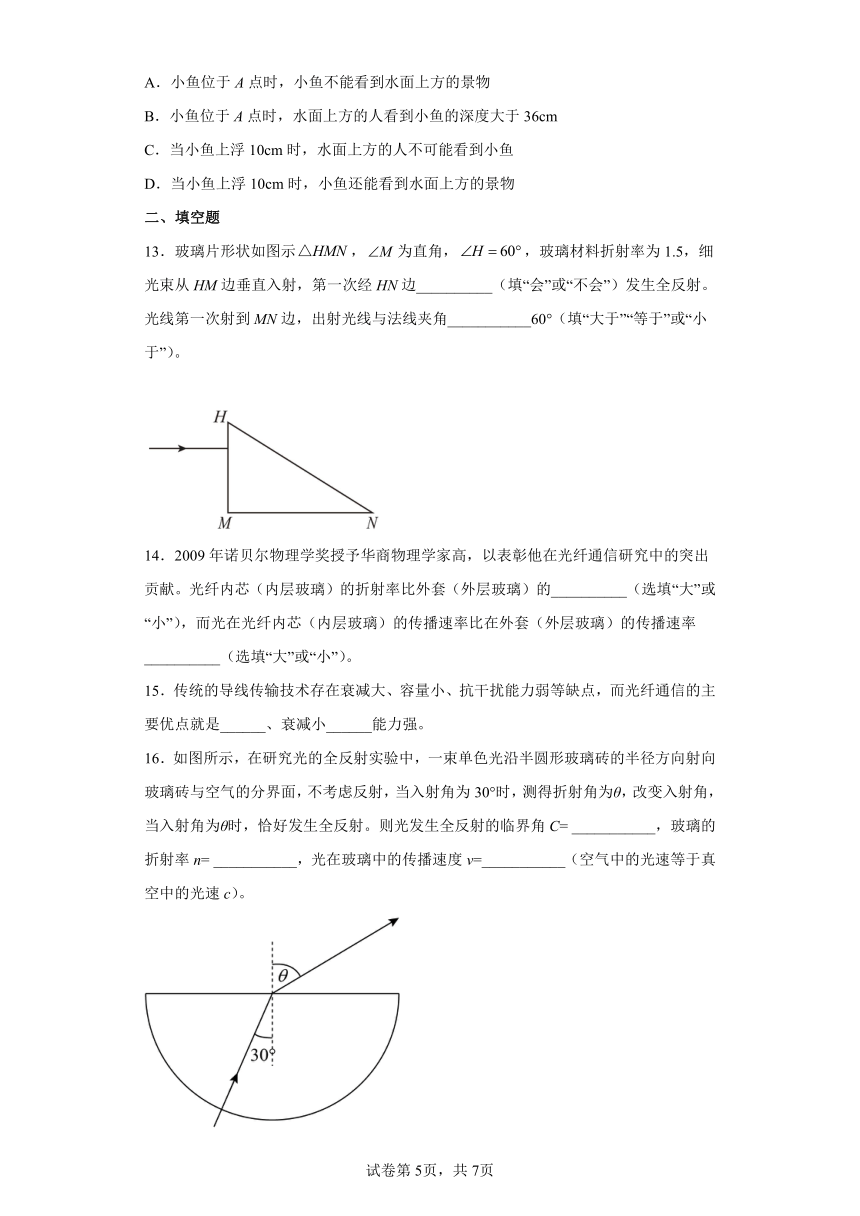
A.小鱼位于A点时,小鱼不能看到水面上方的景物
B.小鱼位于A点时,水面上方的人看到小鱼的深度大于36cm
C.当小鱼上浮10cm时,水面上方的人不可能看到小鱼
D.当小鱼上浮10cm时,小鱼还能看到水面上方的景物
二、填空题
13.玻璃片形状如图示,为直角,,玻璃材料折射率为1.5,细光束从HM边垂直入射,第一次经HN边__________(填“会”或“不会”)发生全反射。光线第一次射到MN边,出射光线与法线夹角___________60°(填“大于”“等于”或“小于”)。
14.2009年诺贝尔物理学奖授予华商物理学家高,以表彰他在光纤通信研究中的突出贡献。光纤内芯(内层玻璃)的折射率比外套(外层玻璃)的__________(选填“大”或“小”),而光在光纤内芯(内层玻璃)的传播速率比在外套(外层玻璃)的传播速率__________(选填“大”或“小”)。
15.传统的导线传输技术存在衰减大、容量小、抗干扰能力弱等缺点,而光纤通信的主要优点就是______、衰减小______能力强。
16.如图所示,在研究光的全反射实验中,一束单色光沿半圆形玻璃砖的半径方向射向玻璃砖与空气的分界面,不考虑反射,当入射角为30°时,测得折射角为θ,改变入射角,当入射角为θ时,恰好发生全反射。则光发生全反射的临界角C= ___________,玻璃的折射率n= ___________,光在玻璃中的传播速度v=___________(空气中的光速等于真空中的光速c)。
17.如图所示,一束平行的绿光从半圆形玻璃砖的平面垂直入射,OC为中心线,已知在半圆弧上的入射点是A的入射光线经折射后与OC的交点为点B,∠AOB=30°,∠ABC=15°,则绿光在该玻璃中的折射率为_________,圆形玻璃砖中有光从半圆面透射区域的圆心角为________;若将入射光改为红光,则光从半圆面透射区域的圆心角将________(选填“变小”、“不变”或“变大”).
三、解答题
18.如图所示,一个是够大的容器中盛满某种透明液体。MN为该液体与空气的水平分界面,其上有一以A点为圆心,半径为d=m的圆形不透光薄片,已知分界面上A点正下方h=3m深处有一点光源O,该点光源发出的光线经不透光薄片的边缘B点处射入空气时,其折射光线与反射光线恰好垂直。
(1)求该透明液体对该光的折射率n;
(2)若在点光源O正下方也为h=3m的P处水平放置一足够大的平面镜,试计算点光源O在分界面MN上照亮区域的面积(取π=3)。
19.光导纤维的工作原理是什么?它是如何传导文字和图像的?
20.如图所示,截面为扇形AOB的玻璃砖固定在水平面上,,在水平面上的C点沿与水平面成30°的方向射出一束光线,照射到AO面上的D点,折射光线水平,刚好照射到AB弧的中点E,已知,光在直空中的传播速度为c,求:
①玻璃砖对光的折射率;
②光从C点传播到E点所用的时间。
21.如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线)。已知玻璃的折射率为。现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线)。求:
(1)从球面射出的光线对应的入射光线与光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离。
22.某公园人工湖畔的夜晚灯光五彩缤纷。如图平静湖面下有一盏灯S(视为点光源),灯S安装在一轨道装置上,且在M点的正下方,游客眼睛恰好位于岸边水面P点正上方1.8m的高度处,水面上Q点处有一浮标(点状物),Q点是水面上PM两点连线的中点,PM两点间距4.8m,此时游客发现灯光刚好被浮标挡住,已知水的折射率。(sin37° = 0.6,sin53° = 0.8)
(1)求灯S离水面的深度h;
(2)如果让灯S沿轨道缓慢向右移动,要使灯发出的光恰好无法从水面P、Q间射出,求该灯应向右移动的距离。(取)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【详解】
半圆柱体的横截面如图所示,OO′为半径,设从A点入射的光线在B点处恰好满足全反射条件,入射角恰好等于临界角C,则由折射定律得
得
C=30°
由几何关系得
∠OO′B=C
则有光线从柱面射出的柱面面积
故选A。
2.C
【解析】
【分析】
【详解】
A.反射光线过圆心,射出时与圆形玻璃砖面垂直,不会发生色散现象,A错误;
B.根据光在玻璃中的传播的速度,红光频率最小,折射率最小,红光在玻璃砖中传播速度最大,B错误;
C.玻璃砖绕O点逆时针缓慢地转过角度θ的过程中,相当于玻璃砖不动,入射光线顺时针转动,折射光线随入射光线顺时针转动,折射光斑沿顺时针方向移动,C正确;
D.由临界角公式可知,紫光折射率最大,临界角最小,玻璃砖旋转过程中弧形屏上最先消失的一定是紫光,D错误。
故选C。
3.C
【解析】
【分析】
【详解】
AB.光从光疏介质射向光密介质时不会发生全反射,AB错误;
C.当入射角最大时,折射角最大,根据折射定律
解得
C正确;
D.根据折射定律
解得
D错误。
故选C。
4.D
【解析】
【详解】
A.当内芯的折射率比外套的大时,光传播时在内芯与外套的界面上才能发生全反射,A错误;
BC.波长越长的光,频率越小,介质对它的折射率n越小,根据公式v=可知,折射率越小的光在光纤中传播的速度越大,BC错误;
D.根据sinC=知,折射率越大,全反射临界角越小,红光的折射率小,则全反射临界角大,若紫光恰能发生全反射,则红光不能发生全反射,D正确。
故选D。
5.C
【解析】
【详解】
AB.由题意画出光路图如图所示,设光线在CD面上的入射角为
根据光路图和反射定律可知
得
由四边形内角和为360°和角度关系可得
∠BCD=∠BAE =90°+=112.5°
故AB错误;
CD.光线在CD和AE界面上恰好发生全反射时,对应着五棱镜折射率的最小值,则
解得
故C正确,D错误。
故选C。
6.A
【解析】
【分析】
【详解】
画出光路图,并根据几何关系标出角度,如图所示
由图可知,介质的折射率
因为
所以折射光线中恰好射到M点的光线不能发生全反射,故A正确,BCD错误。
故选A。
7.A
【解析】
【详解】
要使光信号在内芯和外套的界面发生全反射,则内芯的折射率n1应大于外套的折射率n2,且入射角要大于或等于临界角,所以α应小于某一值,故A正确,BCD错误。
故选A。
8.A
【解析】
【分析】
【详解】
A.频率由波源决定,一束单色光从空气进入水中,光的频率不变,A正确;
B.根据可知,水的折射率较空气大,所以光进入水后的传播速度变小,B错误;
C.光从空气进入水中时,光从光疏进入光密,故折射角小于入射角,C错误;
D.当光从光密介质射入光疏介质时,才会发生全反射现象,而现在是光从空气进入水中,即从光疏进入光密,故不会发生全反射,D错误。
故选A。
9.D
【解析】
【详解】
AB.光线发生全反射的条件是光从光密介质进入光疏介质时,入射角i大于临界角C。光线从图示位置入射,到达OP边时入射角
θ越小,i1越大,发生全反射的可能性越大。根据题意,要在OP边上发生全反射,应满足θ<θ2的条件,故AB错误。
CD.若光线在OP上发生全反射后到达OQ边,入射角
θ越大,i2越大,发生全反射的可能性越大。根据题意,要在OQ边上发生全反射,应满足θ>θ1的条件,故C错误,D正确。
故选D。
10.C
【解析】
【详解】
A.光纤通信的原理是光的全发射,光导纤维内芯的折射率比外套的大,A错误;
B.光从一种介质射入另一种介质时,频率不变,各频率成分的激光束通过光导纤维后频率不变,B错误;
C.各频率成分的激光束在光导纤维传播中折射率大的偏折程度大,对应的频率大的激光出现在前端部分,C正确;
D.频率大的激光出现在前端部分,其波长短,D错误。
故选C。
11.D
【解析】
【详解】
全反射的临界角
故光线在玻璃中会发生全反射,光路图如图所示,
由图中几何关系可得
解得
选项D正确,ABC错误;
故选D。
12.C
【解析】
【详解】
A.临界角为
又因为
所以,不发生全反射,小鱼能看到水面上方的景物,A错误;
B. 根据折射定律,小鱼位于A点时,水面上方的人看到小鱼的深度小于36cm,B错误;
C. 当小鱼上浮10cm时
所以
发生全反射,水面上方的人不可能看到小鱼,小鱼也不能看到水面上方的景物,C正确,D错误。
故选C。
13. 会
【解析】
【详解】
根据题意可知
由图可知
因为
所以会发生全反射,根据几何关系及反射规律可得光线第一次射到MN边,出射光线与法线夹角
14. 大 小
【解析】
【分析】
【详解】
[1]光纤通信是利用了光的全反射原理,全反射的条件是光从光密介质进入光疏介质,入射角大于等于临界角,所以内芯的折射率大于外套的折射率。
[2]由可知,在折射率越大的介质中,光的传播速度越小,所以光在光纤内芯(内层玻璃)的传播速率比在外套(外层玻璃)的传播速率小。
15. 容量大 抗干扰
【解析】
【分析】
【详解】
[1][2]光纤通信的主要优点就是容量大、衰减小、抗干扰能力强。
16. 45°
【解析】
【详解】
[1][2]根据折射定律
解得全反射的临界角
折射率
[3]光在玻璃中的传播速度
17. 1.41 90° 变大
【解析】
【详解】
在A点,由几何知识可得 入射角 i=∠AOB=30°
折射角 r=∠AOB+∠ABC=45°
则介质的折射率为
设光线恰好射到半圆面上D点时发生全反射,其入射角等于临界角C,由sinC=得 C=45°
在D点以下有光从半圆面透射而出,则由对称性可知,圆形玻璃砖中有光从半圆面透射区域的圆心角为90°.
红光的折射率小于绿光,临界角大于绿光,则若将入射光改为红光,则发生全反射的临界点向边缘移动,即光从半圆面透射区域的圆心角将变大.
点睛:作出光路图,运用几何知识求入射角和折射角是解决本题的关键,还要掌握全反射的条件和临界角公式,并能熟练运用.
18.(1);(2)112.5m2
【解析】
【详解】
(1)光线在透明液体中的光路如图所示
由几何关系有
tan i=
解得
i=30°
又
i+r=90°
解得
r=60°
故该透明液体对该光的折射率
(2)设经平面镜反射后射向分界面MN的光线在D点发生全反射,则有
则
设A、D两点间的距离为R,由几何关系可知
所以点光源在分界面MN上照亮的面积为
19.见解析
【解析】
【详解】
光导纤维是由两种或两种以上折射率不同的透明材料通过特殊复合技术制成的复合纤维。光能够在玻璃纤维或塑料纤维中传递是利用光在折射率不同的两种物质的交界面处产生“全反射”作用的原理。由于包层的折射率比芯线折射率小,这样进入芯线的光线在芯线与包层的界面上作多次全反射而曲折前进,不会透过界面,仿佛光线被包层紧紧地封闭在芯线内,使光线只能沿着芯线传送,就好象自来水只能在水管里流动一样;光也有波的特性,因此可以等同于声波,电磁波一样传递信号。用特殊的接受仪器,加上纤维导管的传递作用,就完成了光导纤维的整个工作。
20.①;②
【解析】
【详解】
①由题意知
则
因此光在AO面的入射角
由于DE水平,因此
则光在AO面的折射角
则折射率
②由题意知,OE为的角平分线,则为等腰三角形,则
解得
由几何关系可知,四边形CDEO为平行四边形,因此
光从C点传播到E点所用时间
21.(1);(2)
【解析】
【详解】
(1)如图
从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角时,对应入射光线到光轴的距离最大,设最大距离为l,设n是玻璃的折射率,由全反射临界角的定义有
由几何关系得
联立可得
(2)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为和,由折射定律有
设折射光线与光轴的交点为C,在中,由正弦定理有
由几何关系有
由题意,结合几何关系可得
则有
22.(1)3.2m;(2)1.2m
【解析】
【详解】
(1)根据题意作出如下光路图
根据折射定律有
nsini1= sini2
根据几何关系有
,
计算得
i2= 53°,i1= 37°,h = 3.2m
(2)如果让灯S沿轨道缓慢向右移动,要使灯发出的光恰好无法从水面P、Q间射出,则说明光发生全反射,有
设灯应向右移动的距离为x,根据几何关系有
计算得
x = 1.2m
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,一透明半圆柱体折射率为n = 2,半径为 R、长为 L。一平行光束从半圆柱体的矩形表面垂直射入,有光线从部分柱面射出。则该部分柱面的面积为( )
A. B. C. D.
2.如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合。一束白光沿着半圆柱形玻璃砖的半径从圆弧面垂直BD射到圆心O点上。使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动。在玻璃砖转动过程中,以下说法正确的是( )
A.在弧形屏上可以观察到反射光的色散现象
B.红光在玻璃砖中传播速度最小
C.折射光斑在弧形屏上沿顺时针方向移动
D.玻璃砖旋转过程中弧形屏上最先消失的一定是红光
3.如图所示,一束光从空气中射向折射率为的某种玻璃的表面,θ1表示入射角,则下列说法正确的是( )
A.当时会发生全反射现象
B.只有当时才会发生全反射现象
C.无论入射角θ1是多大,折射角θ2都不会超过45°
D.欲使折射角,应以的角度入射
4.光纤通信中信号传播的主要载体是光导纤维,它的结构如图所示。光导纤维可看成一段直线,其内芯和外套的材料不同,光在内芯中传播,下列关于光导纤维的说法正确的是( )
A.内芯的折射率比外套的大,光传播时在外套与外界的界面上发生全反射
B.波长越长的光在光纤中传播的速度越小
C.频率越大的光在光纤中传播的速度越大
D.若紫光以如图所示角度入射时,恰能在光纤中发生全反射,则改用红光以同样角度入射时,不能在光纤中发生全反射
5.单镜头反光相机简称单反相机,它用一块放置在镜头与感光部件之间的透明平面镜把来自镜头的图像投射到对焦屏上。对焦屏上的图像通过五棱镜的反射进入人眼中。如图所示为单反照相机取景器的示意图,ABCDE为五棱镜的一个截面,AB⊥BC。光线垂直AB射入,分别在CD和EA上发生全反射,且两次全反射的入射角相等,最后光线垂直BC射出。下列说法正确的是( )
A.∠BCD=135°
B.∠BAE和∠BCD不相等
C.该五棱镜折射率的最小值是
D.该五棱镜折射率的最小值是
6.如图所示,扇形AOB为透明柱状介质的横截面,圆心角∠AOB=60°。一束平行于角平分线OM的单色光由OA射入介质,经OA折射的光线恰平行于OB,以下对介质的折射率值及折射光线中恰好射到M点的光线能不能发生全反射的说法正确的是( )
A.,不能发生全反射 B.,能发生全反射
C.,不能发生全反射 D.,能发生全反射
7.如图所示,一光导纤维内芯的折射率为n1,外套的折射率为n2,一束光信号与界面夹角为α由内芯射向外套,要在界面发生全反射,必须满足的条件是 ( )
A.n1>n2,α小于某一值 B.n1
A.光的频率不变
B.光的传播速度变大
C.折射角大于入射角
D.入射角增大到某一角度时将会发生全反射
9.打磨某剖面如图所示的宝石时,必须将OP、OQ边与轴线的夹角θ切磨在θ1<θ<θ2的范围内,才能使从MN边垂直入射的光线,在OP边和OQ边都发生全反射(仅考虑如图所示的光线第一次射到OP边并反射到OQ边后射向MN边的情况),则下列判断正确的是( )
A.若θ>θ2,光线一定在OP边发生全反射
B.若θ>θ2,光线会从OQ边射出
C.若θ>θ1,光线会从OP边射出
D.若θ<θ1,光线会在OP边发生全反射
10.一束包含各频率成分的激光同时进入光导纤维传播,下列说法正确的是( )
A.传播激光信号的光导纤维内芯折射率比外套的低
B.各频率成分的激光束通过光导纤维后频率会降低
C.各频率成分的激光束在光导纤维传播过程中前端部分频率更高
D.各频率成分的激光束在光导纤维传播过程中前端部分波长更长
11.在桌面上有一倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示。有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为1.5,则光束在桌面上形成的光斑半径为( )
A.0.5r B.r C.1.5r D.2.0r
12.如图所示,平静的湖面上漂浮着一圆形荷叶,O为荷叶圆心,O点的正下方A处有一条小鱼(可视为质点),已知O到A的距离,荷叶的半径,水的折射率,则( )
A.小鱼位于A点时,小鱼不能看到水面上方的景物
B.小鱼位于A点时,水面上方的人看到小鱼的深度大于36cm
C.当小鱼上浮10cm时,水面上方的人不可能看到小鱼
D.当小鱼上浮10cm时,小鱼还能看到水面上方的景物
二、填空题
13.玻璃片形状如图示,为直角,,玻璃材料折射率为1.5,细光束从HM边垂直入射,第一次经HN边__________(填“会”或“不会”)发生全反射。光线第一次射到MN边,出射光线与法线夹角___________60°(填“大于”“等于”或“小于”)。
14.2009年诺贝尔物理学奖授予华商物理学家高,以表彰他在光纤通信研究中的突出贡献。光纤内芯(内层玻璃)的折射率比外套(外层玻璃)的__________(选填“大”或“小”),而光在光纤内芯(内层玻璃)的传播速率比在外套(外层玻璃)的传播速率__________(选填“大”或“小”)。
15.传统的导线传输技术存在衰减大、容量小、抗干扰能力弱等缺点,而光纤通信的主要优点就是______、衰减小______能力强。
16.如图所示,在研究光的全反射实验中,一束单色光沿半圆形玻璃砖的半径方向射向玻璃砖与空气的分界面,不考虑反射,当入射角为30°时,测得折射角为θ,改变入射角,当入射角为θ时,恰好发生全反射。则光发生全反射的临界角C= ___________,玻璃的折射率n= ___________,光在玻璃中的传播速度v=___________(空气中的光速等于真空中的光速c)。
17.如图所示,一束平行的绿光从半圆形玻璃砖的平面垂直入射,OC为中心线,已知在半圆弧上的入射点是A的入射光线经折射后与OC的交点为点B,∠AOB=30°,∠ABC=15°,则绿光在该玻璃中的折射率为_________,圆形玻璃砖中有光从半圆面透射区域的圆心角为________;若将入射光改为红光,则光从半圆面透射区域的圆心角将________(选填“变小”、“不变”或“变大”).
三、解答题
18.如图所示,一个是够大的容器中盛满某种透明液体。MN为该液体与空气的水平分界面,其上有一以A点为圆心,半径为d=m的圆形不透光薄片,已知分界面上A点正下方h=3m深处有一点光源O,该点光源发出的光线经不透光薄片的边缘B点处射入空气时,其折射光线与反射光线恰好垂直。
(1)求该透明液体对该光的折射率n;
(2)若在点光源O正下方也为h=3m的P处水平放置一足够大的平面镜,试计算点光源O在分界面MN上照亮区域的面积(取π=3)。
19.光导纤维的工作原理是什么?它是如何传导文字和图像的?
20.如图所示,截面为扇形AOB的玻璃砖固定在水平面上,,在水平面上的C点沿与水平面成30°的方向射出一束光线,照射到AO面上的D点,折射光线水平,刚好照射到AB弧的中点E,已知,光在直空中的传播速度为c,求:
①玻璃砖对光的折射率;
②光从C点传播到E点所用的时间。
21.如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线)。已知玻璃的折射率为。现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线)。求:
(1)从球面射出的光线对应的入射光线与光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离。
22.某公园人工湖畔的夜晚灯光五彩缤纷。如图平静湖面下有一盏灯S(视为点光源),灯S安装在一轨道装置上,且在M点的正下方,游客眼睛恰好位于岸边水面P点正上方1.8m的高度处,水面上Q点处有一浮标(点状物),Q点是水面上PM两点连线的中点,PM两点间距4.8m,此时游客发现灯光刚好被浮标挡住,已知水的折射率。(sin37° = 0.6,sin53° = 0.8)
(1)求灯S离水面的深度h;
(2)如果让灯S沿轨道缓慢向右移动,要使灯发出的光恰好无法从水面P、Q间射出,求该灯应向右移动的距离。(取)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【详解】
半圆柱体的横截面如图所示,OO′为半径,设从A点入射的光线在B点处恰好满足全反射条件,入射角恰好等于临界角C,则由折射定律得
得
C=30°
由几何关系得
∠OO′B=C
则有光线从柱面射出的柱面面积
故选A。
2.C
【解析】
【分析】
【详解】
A.反射光线过圆心,射出时与圆形玻璃砖面垂直,不会发生色散现象,A错误;
B.根据光在玻璃中的传播的速度,红光频率最小,折射率最小,红光在玻璃砖中传播速度最大,B错误;
C.玻璃砖绕O点逆时针缓慢地转过角度θ的过程中,相当于玻璃砖不动,入射光线顺时针转动,折射光线随入射光线顺时针转动,折射光斑沿顺时针方向移动,C正确;
D.由临界角公式可知,紫光折射率最大,临界角最小,玻璃砖旋转过程中弧形屏上最先消失的一定是紫光,D错误。
故选C。
3.C
【解析】
【分析】
【详解】
AB.光从光疏介质射向光密介质时不会发生全反射,AB错误;
C.当入射角最大时,折射角最大,根据折射定律
解得
C正确;
D.根据折射定律
解得
D错误。
故选C。
4.D
【解析】
【详解】
A.当内芯的折射率比外套的大时,光传播时在内芯与外套的界面上才能发生全反射,A错误;
BC.波长越长的光,频率越小,介质对它的折射率n越小,根据公式v=可知,折射率越小的光在光纤中传播的速度越大,BC错误;
D.根据sinC=知,折射率越大,全反射临界角越小,红光的折射率小,则全反射临界角大,若紫光恰能发生全反射,则红光不能发生全反射,D正确。
故选D。
5.C
【解析】
【详解】
AB.由题意画出光路图如图所示,设光线在CD面上的入射角为
根据光路图和反射定律可知
得
由四边形内角和为360°和角度关系可得
∠BCD=∠BAE =90°+=112.5°
故AB错误;
CD.光线在CD和AE界面上恰好发生全反射时,对应着五棱镜折射率的最小值,则
解得
故C正确,D错误。
故选C。
6.A
【解析】
【分析】
【详解】
画出光路图,并根据几何关系标出角度,如图所示
由图可知,介质的折射率
因为
所以折射光线中恰好射到M点的光线不能发生全反射,故A正确,BCD错误。
故选A。
7.A
【解析】
【详解】
要使光信号在内芯和外套的界面发生全反射,则内芯的折射率n1应大于外套的折射率n2,且入射角要大于或等于临界角,所以α应小于某一值,故A正确,BCD错误。
故选A。
8.A
【解析】
【分析】
【详解】
A.频率由波源决定,一束单色光从空气进入水中,光的频率不变,A正确;
B.根据可知,水的折射率较空气大,所以光进入水后的传播速度变小,B错误;
C.光从空气进入水中时,光从光疏进入光密,故折射角小于入射角,C错误;
D.当光从光密介质射入光疏介质时,才会发生全反射现象,而现在是光从空气进入水中,即从光疏进入光密,故不会发生全反射,D错误。
故选A。
9.D
【解析】
【详解】
AB.光线发生全反射的条件是光从光密介质进入光疏介质时,入射角i大于临界角C。光线从图示位置入射,到达OP边时入射角
θ越小,i1越大,发生全反射的可能性越大。根据题意,要在OP边上发生全反射,应满足θ<θ2的条件,故AB错误。
CD.若光线在OP上发生全反射后到达OQ边,入射角
θ越大,i2越大,发生全反射的可能性越大。根据题意,要在OQ边上发生全反射,应满足θ>θ1的条件,故C错误,D正确。
故选D。
10.C
【解析】
【详解】
A.光纤通信的原理是光的全发射,光导纤维内芯的折射率比外套的大,A错误;
B.光从一种介质射入另一种介质时,频率不变,各频率成分的激光束通过光导纤维后频率不变,B错误;
C.各频率成分的激光束在光导纤维传播中折射率大的偏折程度大,对应的频率大的激光出现在前端部分,C正确;
D.频率大的激光出现在前端部分,其波长短,D错误。
故选C。
11.D
【解析】
【详解】
全反射的临界角
故光线在玻璃中会发生全反射,光路图如图所示,
由图中几何关系可得
解得
选项D正确,ABC错误;
故选D。
12.C
【解析】
【详解】
A.临界角为
又因为
所以,不发生全反射,小鱼能看到水面上方的景物,A错误;
B. 根据折射定律,小鱼位于A点时,水面上方的人看到小鱼的深度小于36cm,B错误;
C. 当小鱼上浮10cm时
所以
发生全反射,水面上方的人不可能看到小鱼,小鱼也不能看到水面上方的景物,C正确,D错误。
故选C。
13. 会
【解析】
【详解】
根据题意可知
由图可知
因为
所以会发生全反射,根据几何关系及反射规律可得光线第一次射到MN边,出射光线与法线夹角
14. 大 小
【解析】
【分析】
【详解】
[1]光纤通信是利用了光的全反射原理,全反射的条件是光从光密介质进入光疏介质,入射角大于等于临界角,所以内芯的折射率大于外套的折射率。
[2]由可知,在折射率越大的介质中,光的传播速度越小,所以光在光纤内芯(内层玻璃)的传播速率比在外套(外层玻璃)的传播速率小。
15. 容量大 抗干扰
【解析】
【分析】
【详解】
[1][2]光纤通信的主要优点就是容量大、衰减小、抗干扰能力强。
16. 45°
【解析】
【详解】
[1][2]根据折射定律
解得全反射的临界角
折射率
[3]光在玻璃中的传播速度
17. 1.41 90° 变大
【解析】
【详解】
在A点,由几何知识可得 入射角 i=∠AOB=30°
折射角 r=∠AOB+∠ABC=45°
则介质的折射率为
设光线恰好射到半圆面上D点时发生全反射,其入射角等于临界角C,由sinC=得 C=45°
在D点以下有光从半圆面透射而出,则由对称性可知,圆形玻璃砖中有光从半圆面透射区域的圆心角为90°.
红光的折射率小于绿光,临界角大于绿光,则若将入射光改为红光,则发生全反射的临界点向边缘移动,即光从半圆面透射区域的圆心角将变大.
点睛:作出光路图,运用几何知识求入射角和折射角是解决本题的关键,还要掌握全反射的条件和临界角公式,并能熟练运用.
18.(1);(2)112.5m2
【解析】
【详解】
(1)光线在透明液体中的光路如图所示
由几何关系有
tan i=
解得
i=30°
又
i+r=90°
解得
r=60°
故该透明液体对该光的折射率
(2)设经平面镜反射后射向分界面MN的光线在D点发生全反射,则有
则
设A、D两点间的距离为R,由几何关系可知
所以点光源在分界面MN上照亮的面积为
19.见解析
【解析】
【详解】
光导纤维是由两种或两种以上折射率不同的透明材料通过特殊复合技术制成的复合纤维。光能够在玻璃纤维或塑料纤维中传递是利用光在折射率不同的两种物质的交界面处产生“全反射”作用的原理。由于包层的折射率比芯线折射率小,这样进入芯线的光线在芯线与包层的界面上作多次全反射而曲折前进,不会透过界面,仿佛光线被包层紧紧地封闭在芯线内,使光线只能沿着芯线传送,就好象自来水只能在水管里流动一样;光也有波的特性,因此可以等同于声波,电磁波一样传递信号。用特殊的接受仪器,加上纤维导管的传递作用,就完成了光导纤维的整个工作。
20.①;②
【解析】
【详解】
①由题意知
则
因此光在AO面的入射角
由于DE水平,因此
则光在AO面的折射角
则折射率
②由题意知,OE为的角平分线,则为等腰三角形,则
解得
由几何关系可知,四边形CDEO为平行四边形,因此
光从C点传播到E点所用时间
21.(1);(2)
【解析】
【详解】
(1)如图
从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角时,对应入射光线到光轴的距离最大,设最大距离为l,设n是玻璃的折射率,由全反射临界角的定义有
由几何关系得
联立可得
(2)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为和,由折射定律有
设折射光线与光轴的交点为C,在中,由正弦定理有
由几何关系有
由题意,结合几何关系可得
则有
22.(1)3.2m;(2)1.2m
【解析】
【详解】
(1)根据题意作出如下光路图
根据折射定律有
nsini1= sini2
根据几何关系有
,
计算得
i2= 53°,i1= 37°,h = 3.2m
(2)如果让灯S沿轨道缓慢向右移动,要使灯发出的光恰好无法从水面P、Q间射出,则说明光发生全反射,有
设灯应向右移动的距离为x,根据几何关系有
计算得
x = 1.2m
答案第1页,共2页
答案第1页,共2页
