北师大版九年级下册数学第三章圆单元测试五(附答案)
文档属性
| 名称 | 北师大版九年级下册数学第三章圆单元测试五(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 317.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-17 00:00:00 | ||
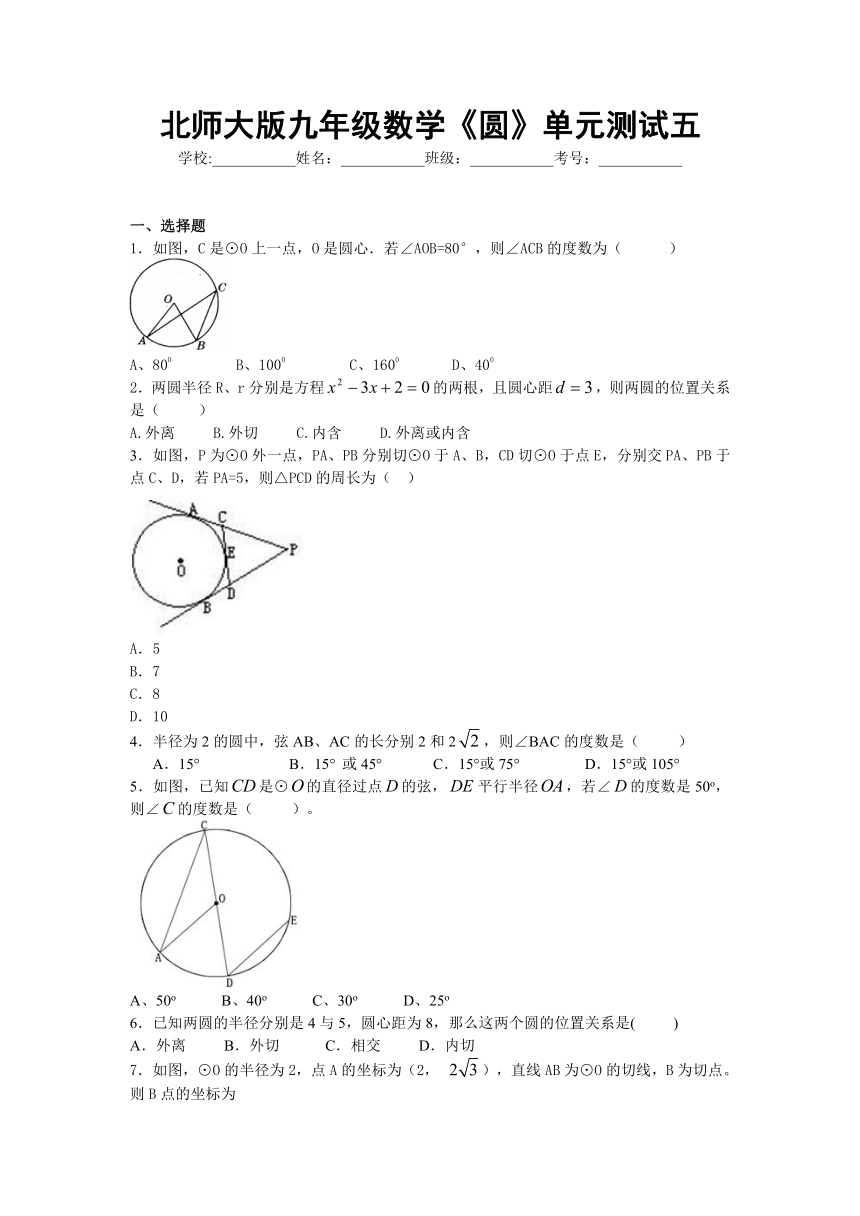
图片预览



文档简介
北师大版九年级数学《圆》单元测试五
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,C是⊙O上一点,O是圆心.若∠AOB=80°,则∠ACB的度数为( )
A、800 B、1000 C、1600 D、400
2.两圆半径R、r分别是方程的两根,且圆心距,则两圆的位置关系是( )
A.外离 B.外切 C.内含 D.外离或内含
3.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为( )
A.5
B.7
C.8
D.10
4.半径为2的圆中,弦AB、AC的长分别2和2,则∠BAC的度数是( )
A.15° B.15° 或45° C.15°或75° D.15°或105°
5.如图,已知是⊙的直径过点的弦,平行半径,若∠的度数是50o,则∠的度数是( )。
A、50o B、40o C、30o D、25o
6.已知两圆的半径分别是4与5,圆心距为8,那么这两个圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
7.如图,⊙O的半径为2,点A的坐标为(2, ),直线AB为⊙O的切线,B为切点。则B点的坐标为
A.() B.()
C.() D.()
8.如图,弦和相交于点,,,则的度数为( )
A.20° B.50° C.70° D.110°
9.已知⊙O的半径为13,AB、CD是⊙O的弦,AB∥CD且AB=10,CD=24,则AB、CD之间的距离为( )
A、7 B、12 C、17 D、7或17
10.如图,以O为圆心,半径为2的圆与反比例函数y=(x>0)的图象交于A、B两点,则的长度为 ( )
A.π B.π C.π D. π
二、填空题
11.如图,将弧BC 沿弦BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是 .
12.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为 .
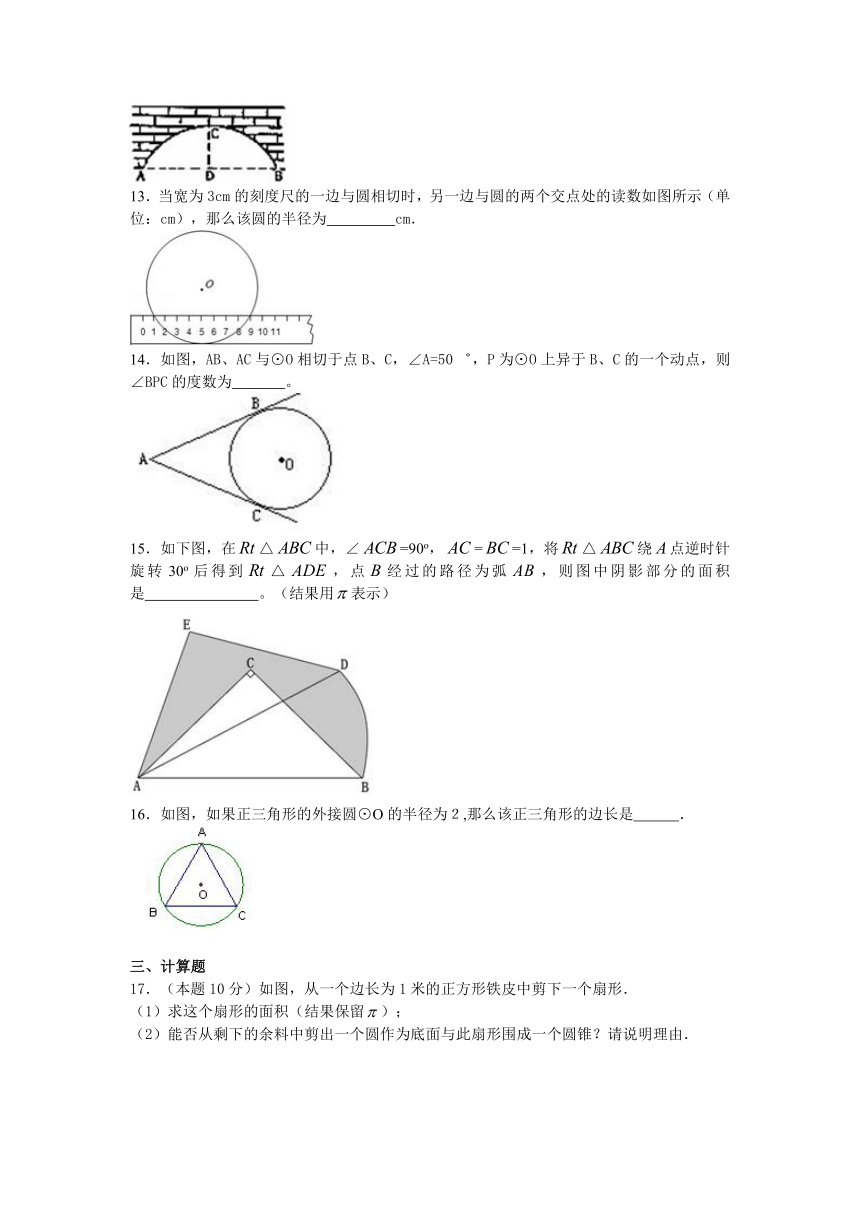
13.当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 cm.
14.如图,AB、AC与⊙O相切于点B、C,∠A=50゜,P为⊙O上异于B、C的一个动点,则∠BPC的度数为 。
15.如下图,在△中,∠=90o,==1,将△绕点逆时针旋转30o后得到△,点经过的路径为弧,则图中阴影部分的面积是 。(结果用表示)
16.如图,如果正三角形的外接圆⊙O的半径为2,那么该正三角形的边长是 .
三、计算题
17.(本题10分)如图,从一个边长为1米的正方形铁皮中剪下一个扇形.
(1)求这个扇形的面积(结果保留);
(2)能否从剩下的余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.
18.如图,点A、B在直线MN上,AB=11cm,⊙A、⊙B的半径为1cm. ⊙A以每秒2cm的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)当t=1时,AB= cm;当t=6时,AB= cm;
(2)问点A出发后多少秒两圆相切?
四、解答题
19.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)判断线段AC与AE是否相等,并说明理由;
(2)求过A、C、D三点的圆的直径.
20.问题:如图1,在正方形ABCD内有一点
P,PA=,PB=,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
请你参考小明同学的思路,解决下列问题:
(1) 图2中∠BPC的度数为 ;
(2) 如图3,若在正六边形ABCDEF内有一点P,且PA=,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
21.已知OA、OB是⊙O的两条半径,且OA⊥BC,C为OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD,交OC过于点E。
(1)求证:CD=CE;
(2)若将图1中的半径OB所在的直线向上平行移动,交⊙O于,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
22.(1)已知:如图1,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.求证:DE=DF.
(2)如图2,已知△ABC内接于⊙O,AC是⊙O的直径,D是弧AB的中点,过点D作直线BC的垂线,分别交CB,CA的延长线于E,F,求证:EF是⊙O的切线.
23.已知: 如图, AB是⊙O的直径,⊙O过AC的中点D, DE切⊙O于点D, 交BC于点E.
(1)求证: DE⊥BC;
(2)如果CD=4,CE=3,求⊙O的半径.
24.如图,⊙O的直径AB平分弦CD, CD =10cm, AP: PB=1 : 5.求⊙O的半径.
25.如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)若AD2=AC·AE,求证:BC=CD.
参考答案
1.D2.B3.D4.D5.D 6.C7.D8.B9.D10.C11.12.6.5米13.
14.65゜或115゜15. 16.17.(1)(2)不能18.(1)9;1;(2)3秒、秒、11秒、13秒19.(1)AC=AE;(2)20.(1)135° (2) 120°
21.
22.
23.证明:(1)连结OD
∵DE切⊙O于点D
∴DE⊥OD, ∴∠ODE=900 又∵AD=DC, AO=OB
∴OD//BC
∴∠DEC=∠ODE=900, ∴DE⊥BC
(2)连结BD.
∵AB是⊙O的直径, ∴∠ADB=900
∴BD⊥AC, ∴∠BDC=900
又∵DE⊥BC, △RtCDB∽△RtCED
∴, ∴BC=
又∵OD=BC
∴OD=, 即⊙O的半径为
24.连接CO,设圆的半径为r,
∵直径AB平分弦CD
∴AB垂直CD
∵AP:PB=1 : 5 ∴PO=r
∴r2=52+(r)2 得r=3
25.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,C是⊙O上一点,O是圆心.若∠AOB=80°,则∠ACB的度数为( )
A、800 B、1000 C、1600 D、400
2.两圆半径R、r分别是方程的两根,且圆心距,则两圆的位置关系是( )
A.外离 B.外切 C.内含 D.外离或内含
3.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为( )
A.5
B.7
C.8
D.10
4.半径为2的圆中,弦AB、AC的长分别2和2,则∠BAC的度数是( )
A.15° B.15° 或45° C.15°或75° D.15°或105°
5.如图,已知是⊙的直径过点的弦,平行半径,若∠的度数是50o,则∠的度数是( )。
A、50o B、40o C、30o D、25o
6.已知两圆的半径分别是4与5,圆心距为8,那么这两个圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
7.如图,⊙O的半径为2,点A的坐标为(2, ),直线AB为⊙O的切线,B为切点。则B点的坐标为
A.() B.()
C.() D.()
8.如图,弦和相交于点,,,则的度数为( )
A.20° B.50° C.70° D.110°
9.已知⊙O的半径为13,AB、CD是⊙O的弦,AB∥CD且AB=10,CD=24,则AB、CD之间的距离为( )
A、7 B、12 C、17 D、7或17
10.如图,以O为圆心,半径为2的圆与反比例函数y=(x>0)的图象交于A、B两点,则的长度为 ( )
A.π B.π C.π D. π
二、填空题
11.如图,将弧BC 沿弦BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是 .
12.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为 .
13.当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 cm.
14.如图,AB、AC与⊙O相切于点B、C,∠A=50゜,P为⊙O上异于B、C的一个动点,则∠BPC的度数为 。
15.如下图,在△中,∠=90o,==1,将△绕点逆时针旋转30o后得到△,点经过的路径为弧,则图中阴影部分的面积是 。(结果用表示)
16.如图,如果正三角形的外接圆⊙O的半径为2,那么该正三角形的边长是 .
三、计算题
17.(本题10分)如图,从一个边长为1米的正方形铁皮中剪下一个扇形.
(1)求这个扇形的面积(结果保留);
(2)能否从剩下的余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.
18.如图,点A、B在直线MN上,AB=11cm,⊙A、⊙B的半径为1cm. ⊙A以每秒2cm的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)当t=1时,AB= cm;当t=6时,AB= cm;
(2)问点A出发后多少秒两圆相切?
四、解答题
19.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)判断线段AC与AE是否相等,并说明理由;
(2)求过A、C、D三点的圆的直径.
20.问题:如图1,在正方形ABCD内有一点
P,PA=,PB=,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
请你参考小明同学的思路,解决下列问题:
(1) 图2中∠BPC的度数为 ;
(2) 如图3,若在正六边形ABCDEF内有一点P,且PA=,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
21.已知OA、OB是⊙O的两条半径,且OA⊥BC,C为OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD,交OC过于点E。
(1)求证:CD=CE;
(2)若将图1中的半径OB所在的直线向上平行移动,交⊙O于,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
22.(1)已知:如图1,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.求证:DE=DF.
(2)如图2,已知△ABC内接于⊙O,AC是⊙O的直径,D是弧AB的中点,过点D作直线BC的垂线,分别交CB,CA的延长线于E,F,求证:EF是⊙O的切线.
23.已知: 如图, AB是⊙O的直径,⊙O过AC的中点D, DE切⊙O于点D, 交BC于点E.
(1)求证: DE⊥BC;
(2)如果CD=4,CE=3,求⊙O的半径.
24.如图,⊙O的直径AB平分弦CD, CD =10cm, AP: PB=1 : 5.求⊙O的半径.
25.如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)若AD2=AC·AE,求证:BC=CD.
参考答案
1.D2.B3.D4.D5.D 6.C7.D8.B9.D10.C11.12.6.5米13.
14.65゜或115゜15. 16.17.(1)(2)不能18.(1)9;1;(2)3秒、秒、11秒、13秒19.(1)AC=AE;(2)20.(1)135° (2) 120°
21.
22.
23.证明:(1)连结OD
∵DE切⊙O于点D
∴DE⊥OD, ∴∠ODE=900 又∵AD=DC, AO=OB
∴OD//BC
∴∠DEC=∠ODE=900, ∴DE⊥BC
(2)连结BD.
∵AB是⊙O的直径, ∴∠ADB=900
∴BD⊥AC, ∴∠BDC=900
又∵DE⊥BC, △RtCDB∽△RtCED
∴, ∴BC=
又∵OD=BC
∴OD=, 即⊙O的半径为
24.连接CO,设圆的半径为r,
∵直径AB平分弦CD
∴AB垂直CD
∵AP:PB=1 : 5 ∴PO=r
∴r2=52+(r)2 得r=3
25.
