北师大版九年级数学《圆》单元测试三(有答案)
文档属性
| 名称 | 北师大版九年级数学《圆》单元测试三(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 196.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-17 00:00:00 | ||
图片预览



文档简介
北师大版九年级数学《圆》单元测试三
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知⊙O中,弦AB的长等于半径,P为弦AB所对的弧上一动点,则∠APB的度数为( )
A. 30o B. 150o C. 30o或150o D. 60o或120o
2.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
3.下列说法错误的是( )
A、直径是弦 B、最长的弦是直径
C、垂直弦的直径平分弦 D、任意三个点确定一个圆
4.如图,A、B、C三点是⊙O上的点,∠ABO=55°,则∠BCA的度数是
A.55°
B.70°
C.35°
D.27.5°
5.如下图所示,在⊙内有折线,其中=8,,=12,∠=∠=60o,则的长为( )。
A、19 B、16 C、18 D、20
6.下列语句中不正确的有( )
①长度相等的两条弧是等弧 ②平分弦的直径垂直于弦 ③直径所对的圆周角是直角④一条弧所对的圆心角等于它所对圆周角的2倍
A.3个 B.2个 C.1个 D.以上都不对
7.如图,⊙O的半径为1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是( )
A.
B.
C.
D.
8.如图是一个“众志成城,奉献爱心”的图标,图标中两圆的位置关系是 ( )
A.外离 B.外切 C.相交 D.内切
9.如图,平面直角坐标系中,⊙P经过平面直角坐标系的原点O,且分别交x轴、y轴于A、B两点。C为弧ACB的中点,A(6,0)、AC=5,则点B的坐标是( )
A、(0,7) B、(0,6)
C、(0,8) D、(0,6)
10.如图,当半径为30cm的转动轮转过120°圆心角时,传送带上的物体A平移的距离为( )
A. 900лcm B.300лcm
C. 60лcm D.20лcm
二、填空题
11.如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=24o,则∠EFG= .
12.一个圆锥的底面半径为3,高为4,则圆锥的侧面积是 。
13.如图,以点P为圆心的圆弧与X轴交于A,B两点,点P的坐标为(4,2)点A的坐标(2,0)则点B的坐标为 .
14.如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB = 20°,则∠OCD = _____ ________.
15.一个圆的直径增加( )厘米后,它的周长就增加π厘米。
16.如图,点C、D在以AB为直径的⊙O上,若∠BDC=28°,则∠ABC= .
三、计算题
17.(8分)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
请完成下列填空:
①请在图中确定并点出该圆弧所在圆心D点的位置,圆心D 坐标 ;
②⊙D的半径= (结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,求圆锥的侧面积
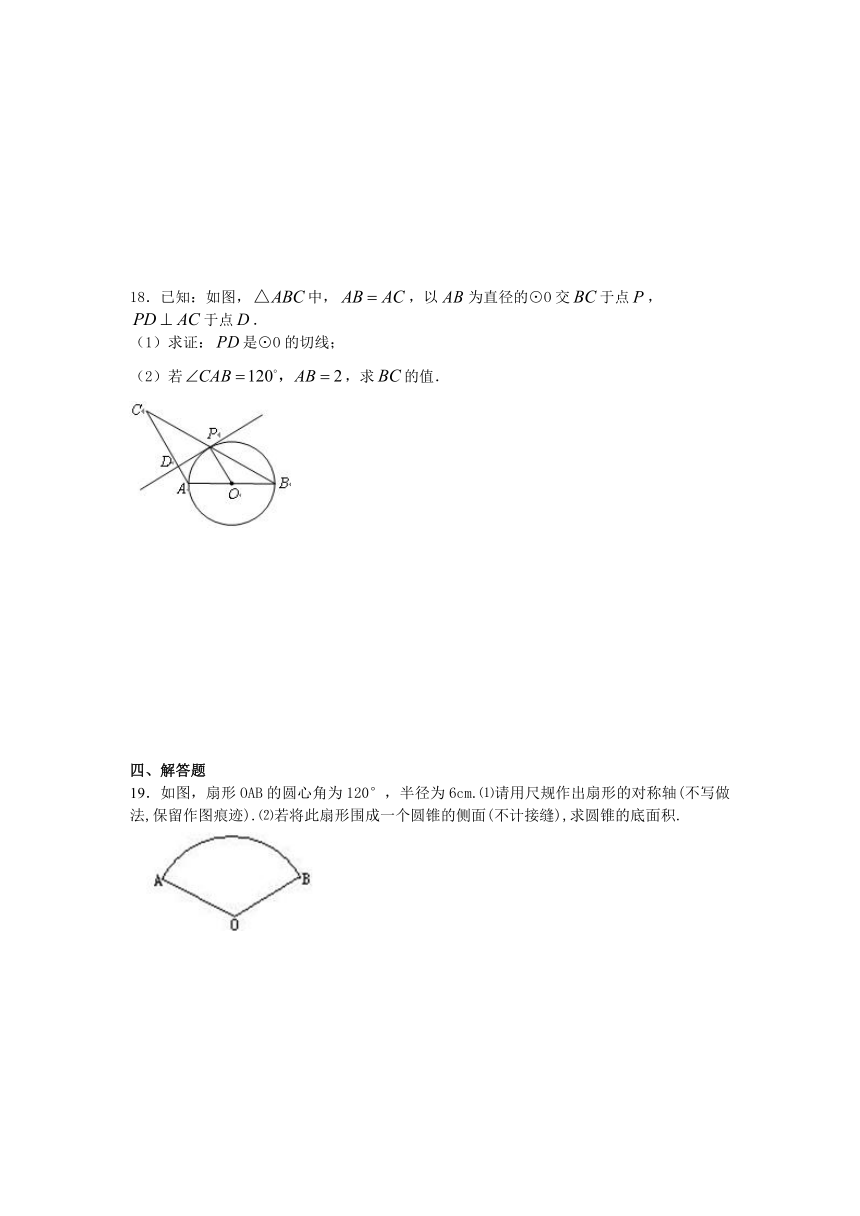
18.已知:如图,中,,以为直径的⊙O交于点,
于点.
(1)求证:是⊙O的切线;
(2)若,求的值.
四、解答题
19.如图,扇形OAB的圆心角为120°,半径为6cm.⑴请用尺规作出扇形的对称轴(不写做法,保留作图痕迹).⑵若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面积.
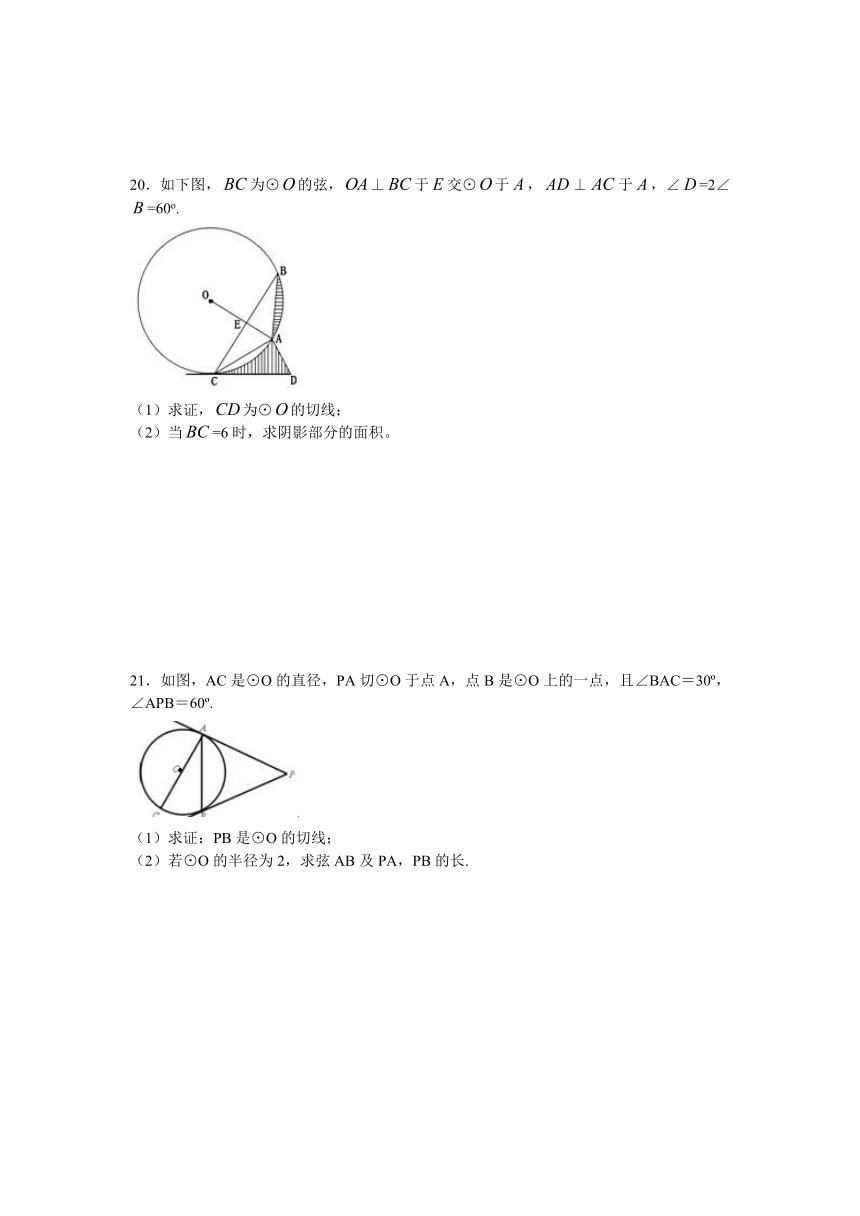
20.如下图,为⊙的弦,⊥于交⊙于,⊥于,∠=2∠=60o.
(1)求证,为⊙的切线;
(2)当=6时,求阴影部分的面积。
21.如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30o,∠APB=60o.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求弦AB及PA,PB的长.
22.如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
23.如图,AB是⊙的直径,弦CD与AB交于点E,过点作⊙的切线与的延长线交于点,如果,,为的中点.
(1)求证:;
(2)求AB的长.
24.已知:如图,∠PAC=30o,在射线AC上顺次截取AD=3 cm,DB=10 cm,以DB为直径作⊙O,交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
25.如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,.
(1)求证:直线PB是⊙O的切线;
(2)求cos∠BCA的值.
参考答案
1.C
2.B
3.D
4.C
5.D
6.B
7.B
8.B
9.C
10.D
11.36o
12.15π
13.(6,0)
14.65°
15.1
16.62°
17.(1)D(2,0)(2)(3)5π
18.(1)略;(2)
19.(1)略(2)
20.(1)略;(2)
21.(1)略;(2)2
22. (1)略
(2) AB=.
(3)直线FA与⊙O相切.
23.解:(1)联结
∵为的切线
∴⊥即=
∵为的中点, ∴
∴
∵为的直径,
∴
∵=
∴
∴
(2) 作
∵⊥,∴
∵,,∴
可得
∵∴
中,
∴=:
在中,
∴
24.4厘米,6厘米
25.解:(1)证明:连接OB、OP
∵ 且∠D=∠D
∴ △BDC∽△PDO
∴ ∠DBC=∠DPO ∴ BC∥OP
∴ ∠BCO=∠POA ∠CBO=∠BOP
∵ OB=OC ∴ ∠OCB=∠CBO ∴ ∠BOP=∠POA
又∵ OB=OA OP=OP ∴ △BOP≌△AOP ∴ ∠PBO=∠PAO
又∵ PA⊥AC ∴ ∠PBO=90° ∴ 直线PB是⊙O的切线
(2)由(1)知∠BCO=∠POA 设PB,则
又∵ ∴
又∵ BC∥OP ∴ ∴
∴ ∴ ∴ cos∠BCA=cos∠POA=
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知⊙O中,弦AB的长等于半径,P为弦AB所对的弧上一动点,则∠APB的度数为( )
A. 30o B. 150o C. 30o或150o D. 60o或120o
2.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
3.下列说法错误的是( )
A、直径是弦 B、最长的弦是直径
C、垂直弦的直径平分弦 D、任意三个点确定一个圆
4.如图,A、B、C三点是⊙O上的点,∠ABO=55°,则∠BCA的度数是
A.55°
B.70°
C.35°
D.27.5°
5.如下图所示,在⊙内有折线,其中=8,,=12,∠=∠=60o,则的长为( )。
A、19 B、16 C、18 D、20
6.下列语句中不正确的有( )
①长度相等的两条弧是等弧 ②平分弦的直径垂直于弦 ③直径所对的圆周角是直角④一条弧所对的圆心角等于它所对圆周角的2倍
A.3个 B.2个 C.1个 D.以上都不对
7.如图,⊙O的半径为1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是( )
A.
B.
C.
D.
8.如图是一个“众志成城,奉献爱心”的图标,图标中两圆的位置关系是 ( )
A.外离 B.外切 C.相交 D.内切
9.如图,平面直角坐标系中,⊙P经过平面直角坐标系的原点O,且分别交x轴、y轴于A、B两点。C为弧ACB的中点,A(6,0)、AC=5,则点B的坐标是( )
A、(0,7) B、(0,6)
C、(0,8) D、(0,6)
10.如图,当半径为30cm的转动轮转过120°圆心角时,传送带上的物体A平移的距离为( )
A. 900лcm B.300лcm
C. 60лcm D.20лcm
二、填空题
11.如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=24o,则∠EFG= .
12.一个圆锥的底面半径为3,高为4,则圆锥的侧面积是 。
13.如图,以点P为圆心的圆弧与X轴交于A,B两点,点P的坐标为(4,2)点A的坐标(2,0)则点B的坐标为 .
14.如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB = 20°,则∠OCD = _____ ________.
15.一个圆的直径增加( )厘米后,它的周长就增加π厘米。
16.如图,点C、D在以AB为直径的⊙O上,若∠BDC=28°,则∠ABC= .
三、计算题
17.(8分)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
请完成下列填空:
①请在图中确定并点出该圆弧所在圆心D点的位置,圆心D 坐标 ;
②⊙D的半径= (结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,求圆锥的侧面积
18.已知:如图,中,,以为直径的⊙O交于点,
于点.
(1)求证:是⊙O的切线;
(2)若,求的值.
四、解答题
19.如图,扇形OAB的圆心角为120°,半径为6cm.⑴请用尺规作出扇形的对称轴(不写做法,保留作图痕迹).⑵若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面积.
20.如下图,为⊙的弦,⊥于交⊙于,⊥于,∠=2∠=60o.
(1)求证,为⊙的切线;
(2)当=6时,求阴影部分的面积。
21.如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30o,∠APB=60o.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求弦AB及PA,PB的长.
22.如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
23.如图,AB是⊙的直径,弦CD与AB交于点E,过点作⊙的切线与的延长线交于点,如果,,为的中点.
(1)求证:;
(2)求AB的长.
24.已知:如图,∠PAC=30o,在射线AC上顺次截取AD=3 cm,DB=10 cm,以DB为直径作⊙O,交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
25.如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,.
(1)求证:直线PB是⊙O的切线;
(2)求cos∠BCA的值.
参考答案
1.C
2.B
3.D
4.C
5.D
6.B
7.B
8.B
9.C
10.D
11.36o
12.15π
13.(6,0)
14.65°
15.1
16.62°
17.(1)D(2,0)(2)(3)5π
18.(1)略;(2)
19.(1)略(2)
20.(1)略;(2)
21.(1)略;(2)2
22. (1)略
(2) AB=.
(3)直线FA与⊙O相切.
23.解:(1)联结
∵为的切线
∴⊥即=
∵为的中点, ∴
∴
∵为的直径,
∴
∵=
∴
∴
(2) 作
∵⊥,∴
∵,,∴
可得
∵∴
中,
∴=:
在中,
∴
24.4厘米,6厘米
25.解:(1)证明:连接OB、OP
∵ 且∠D=∠D
∴ △BDC∽△PDO
∴ ∠DBC=∠DPO ∴ BC∥OP
∴ ∠BCO=∠POA ∠CBO=∠BOP
∵ OB=OC ∴ ∠OCB=∠CBO ∴ ∠BOP=∠POA
又∵ OB=OA OP=OP ∴ △BOP≌△AOP ∴ ∠PBO=∠PAO
又∵ PA⊥AC ∴ ∠PBO=90° ∴ 直线PB是⊙O的切线
(2)由(1)知∠BCO=∠POA 设PB,则
又∵ ∴
又∵ BC∥OP ∴ ∴
∴ ∴ ∴ cos∠BCA=cos∠POA=
