2.5受迫振动共振练习(word版含答案)
文档属性
| 名称 | 2.5受迫振动共振练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览




文档简介
粤教版(2019)选择性必修一 2.5 受迫振动 共振
一、单选题
1.正在运转的机器,当其飞轮以角速度匀速转动时,机器的振动不强烈,切断电源,飞轮的转动逐渐慢下来,在某一小段时间内机器却发生了强烈的振动,此后飞轮转速继续变慢,机器的振动也随之减弱,在机器停下来之后若重新启动机器,使飞轮转动的角速度从0较缓慢地增大到,在这一过程中( )
A.机器一定不会发生强烈的振动
B.机器不一定还会发生强烈的振动
C.若机器发生强烈振动,强烈振动可能发生在飞轮角速度为时
D.若机器发生强烈振动,强烈振动时飞轮的角速度肯定不为
2.下列说法正确的是( )
A.在同一地点,单摆做简谐振动的周期与其摆长成正比
B.弹簧振子做简谐振动时,振动系统的势能与动能之和逐渐减少
C.弹簧振子做简谐振动时,弹簧的劲度系数越大,单摆做简谐振动的周期越大
D.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率
3.如图所示为CCTV10“我爱发明”节目中介绍的松果采摘机,松果采摘机利用机械臂抱紧树干,通过采摘振动头振动而摇动树干,使得松果脱落。下列说法正确是( )
A.工作中,树干的振动频率小于采摘振动头的振动频率
B.采摘振动头振动频率越高,采摘落果的效果一定越好
C.采摘振动头振动频率减小,树干的振动幅度可能增大
D.若采摘振动头停止振动,树干的振动频率会逐渐减小
4.松子以其独特的香味、丰富的植物脂肪含量,成为了坚果界的宠儿。在我国东北地区,为了提高采摘效率,工程技术人员发明了振动器,将振动器固定在树干上,如图所示,机车带动振动器振动,使松果落下。则( )
A.针对不同树干,落果效果最好时的振动频率相同
B.随着振动器频率的增加,树干振动的幅度一定增大
C.振动器正常工作时,不同树干的振动频率始终与振动器的振动频率相同
D.振动器对不同树干作用结束后,树干的自由振动频率相同
5.自由摆动的秋千摆动幅度越来越小,下列说法正确的是( )
A.机械能守恒 B.能量正在消失
C.只有动能和势能相互转化 D.减少的机械能转化为内能
6.部队经过桥梁时,规定不许齐步走,登山运动员登雪山时,不许高声叫喊,主要原因是( )
A.减轻对桥的压力,避免产生回声
B.减少对桥、雪山的冲击力
C.避免使桥发生共振和使雪山发生共振
D.使桥受到的压力更不均匀,使登山运动员耗散能量
7.为了交通安全,常在公路上设置如图所示的减速带,减速带使路面稍微拱起以达到使车辆减速的目的。一排等间距设置的减速带,可有效降低车速。如果某路面上的减速带间距为2m,一辆固有频率为4Hz的汽车匀速驶过这排减速带,下列说法正确的是( )
A.汽车速度越大,颠簸一定越厉害
B.汽车以约8m/s的速度行驶时颠簸最厉害
C.汽车以约8m/s的速度行驶时颠簸最轻
D.汽车以10m/s的速度行驶时,其振动频率为4Hz
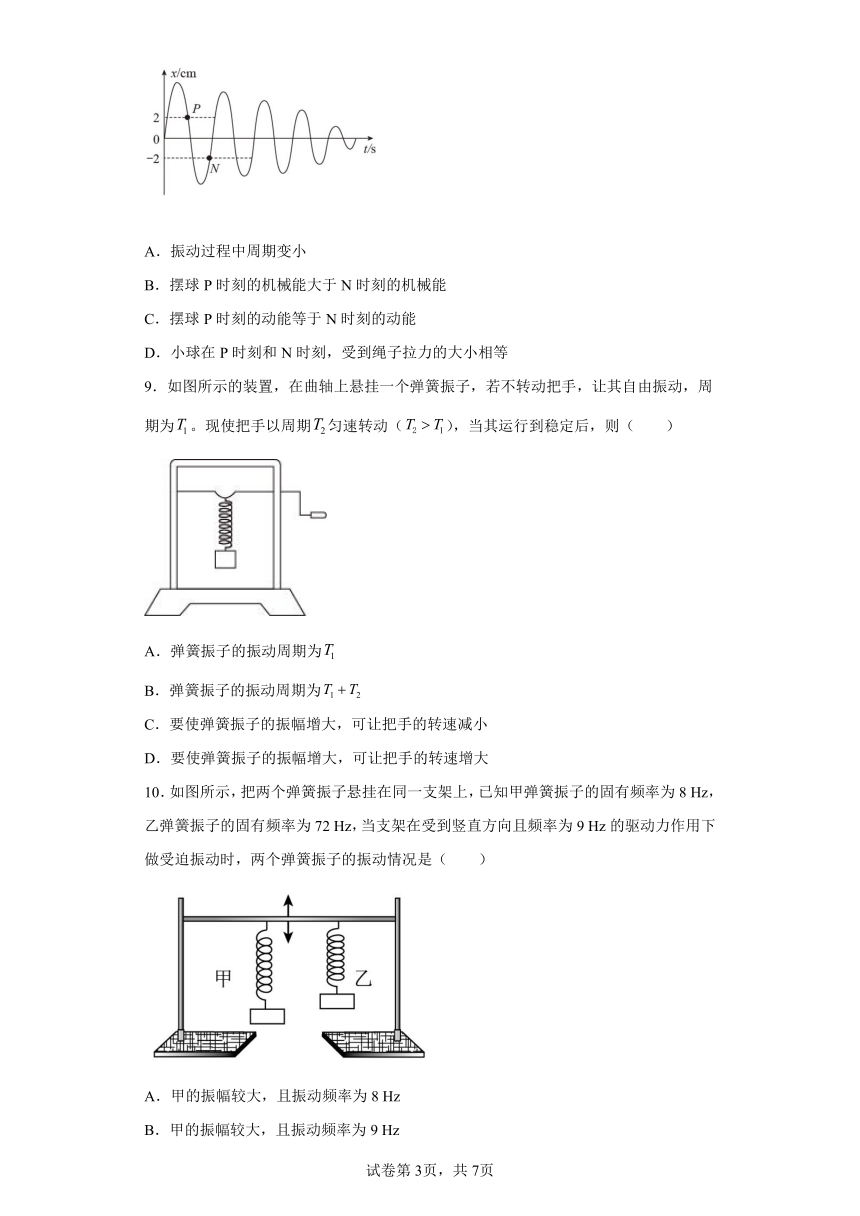
8.如图所示是某单摆做阻尼振动的振动图线,下列说法正确的是( )
A.振动过程中周期变小
B.摆球P时刻的机械能大于N时刻的机械能
C.摆球P时刻的动能等于N时刻的动能
D.小球在P时刻和N时刻,受到绳子拉力的大小相等
9.如图所示的装置,在曲轴上悬挂一个弹簧振子,若不转动把手,让其自由振动,周期为。现使把手以周期匀速转动(),当其运行到稳定后,则( )
A.弹簧振子的振动周期为
B.弹簧振子的振动周期为
C.要使弹簧振子的振幅增大,可让把手的转速减小
D.要使弹簧振子的振幅增大,可让把手的转速增大
10.如图所示,把两个弹簧振子悬挂在同一支架上,已知甲弹簧振子的固有频率为8 Hz,乙弹簧振子的固有频率为72 Hz,当支架在受到竖直方向且频率为9 Hz的驱动力作用下做受迫振动时,两个弹簧振子的振动情况是( )
A.甲的振幅较大,且振动频率为8 Hz
B.甲的振幅较大,且振动频率为9 Hz
C.乙的振幅较大,且振动频率为9 Hz
D.乙的振幅较大,且振动频率为72 Hz
11.高压输电线路塔杆较高,杆距较大,当输电线受到风吹动时,会发生较强烈的振动,输电线会因周期性的弯折发生破坏,为此,需要在靠近塔杆悬点处加挂一个小锤,如图所示。下列说法正确的是( )
A.小锤的作用是防雷电
B.小锤的作用是为了减弱输电线振动的幅度
C.小锤的振动与输电线振动是同步的
D.小锤的规格与杆距无关
12.在敲响古刹里的大钟时,有的同学发现,停止对大钟的撞击后,大钟仍“余音未绝”,分析其原因是( )
A.大钟的回声 B.大钟在继续振动
C.人的听觉发生“暂留”的缘故 D.大钟虽停止振动,但空气仍在振动
13.在喜剧电影《功夫》中,包租婆的“狮子吼”可以将酒杯震碎。若我们用手指轻弹同样的酒杯,听到清脆的声音,并测得该声音的频率为500,已知空气中的声速为340,则包租婆的“狮子吼”声波的波长约为( )
A.0.68m B.1.32m C.1.47m D.2.94m
14.下列说法不正确的是( )
A.弹簧振子做简谐振动时,振动系统的势能与动能之和保持不变
B.在同一地点,当摆长不变时,摆球质量越大,单摆做简谐振动的周期不变
C.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率
D.已知弹簧振子初始时刻的位置及其振动周期,就可知振子在任意时刻运动速度的方向
15.如图所示的装置,弹簧振子的固有频率是。现匀速转动把手,给弹簧振子以周期性的驱动力,测得弹簧振子振动达到稳定时的频率为,则把手转动的频率逐渐缓慢增大时,下列说法中正确的是( )
A.弹簧振子的振动越来越剧烈
B.弹簧振子的振动越来越弱
C.弹簧振子的振动先越来越剧烈再越来越弱
D.弹簧振子的振动先越来越弱再越来越剧烈
二、填空题
16.如图所示是用来测量各种发动机转速的转速计原理图。在同一铁支架上焊有固有频率依次为、80Hz、60Hz、40Hz的四个钢片将端与正在转动的电动机接触,发现钢片振幅最大,则此时振动频率为____________,电动机转速为___________。
17.如图所示,一个竖直圆盘转动时,固定在圆盘上的小圆柱带动一个T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球组成的振动系统,小球浸没在水中;当圆盘转动一会静止后,小球做____振动(选填“阻尼”,“自由”,“受迫”);若弹簧和小球构成的系统振动频率约为3Hz,现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定,小球的振动频率为_____Hz;逐渐改变圆盘的转动周期,当小球振动的振幅达到最大时,此时圆盘的周期为____s。
18.判断该说法的正误:
物体做受迫振动时,其振动频率与固有频率无关。( )
三、解答题
19.如图所示,在曲轴A上悬挂一个弹簧振子,如果转动把手,曲轴可以带动弹簧振子上下振动。问:
(1)开始时不转动把手,而用手往下拉振子,然后放手让振子上下振动,测得振子在10 s内完成20次全振动,振子做什么振动?其固有周期和固有频率各是多少?若考虑摩擦和空气阻力,振子做什么振动?
(2)在振子正常振动过程中,以转速4r/s匀速转动把手,振子的振动稳定后,振子做什么运动?其周期是多少?
(3)若要振子振动的振幅最大,把手的转速应多大?为什么?
20.上海中心大厦高632m,上面安装有重达1000t的风阻尼器。请查阅相关资料,了解它的作用及工作原理。
21.如图所示是一个单摆的共振曲线。
(1)试估计此单摆的摆长;(g取)
(2)若摆长增大,共振曲线的峰将怎样移动?
22.汽车的车身是装在弹簧上的,如果这个系统的固有周期是1.5 s,汽车在一条起伏不平的路上行驶,路上各凸起处大约都相隔8 m,汽车以多大速度行驶时,车身上下颠簸得最剧烈?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
【详解】
当驱动力频率等于系统的固有频率时会产生共振,飞轮在转速逐渐减小的过程中,机器出现强烈的振动,说明发生共振现象,此时飞轮转动的频率等于机器本身的固有频率;当机器重新启动时,飞轮转速缓慢增大的过程中,一旦达到共振条件,机器一定还会发生强烈的振动.由题意可知,发生强烈共振时,飞轮的角速度一定小于ω0。
故选D。
2.D
【解析】
【分析】
【详解】
A.根据单摆的周期公式
分析知,在同一地点,单摆做简谐振动的周期的平方与其摆长成正比,A错误;
B.弹簧振子做简谐振动时,只有重力或弹簧的弹力做功,振动系统的势能与动能之和保持不变,B错误;
C.根据弹簧振子的周期公式
可知弹簧的劲度系数越大,弹簧振子做简谐振动的周期越小,C错误;
D.根据受迫振动的特点可知,系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,D正确。
故选D。
3.C
【解析】
【详解】
A.受迫振动的频率等于驱动力频率,工作中,树干的振动频率等于采摘振动头的振动频率,故A错误;
BC.当采摘振动头振动频率等于树干的固有频率时,将发生共振现象,此时树干的振幅最大,采摘落果的效果最好,若开始时采摘振动头振动频率大于树干的固有频率,则增大频率后,树干的振幅反而减小,采摘落果的效果更差,而此时若减小采摘振动头振动频率,则树干的振幅会增大,故B错误,C正确;
D.若采摘振动头停止振动,树干的振动频率不变,振幅逐渐减小,故D错误。
故选C。
4.C
【解析】
【详解】
A.不同的树干,固有频率可能不同,根据共振的产生条件,针对不同树干,落果效果最好时的振动频率可能不相同,故A错误;
B.只有振动器的频率与树干的固有频率相同时,树干振动的幅度最大,所以随着振动器频率的增加,树干振动的幅度不一定增大,故B错误;
C.树干在振动器的振动下,做受迫振动,所以振动器正常工作时,不同树干的振动频率始终与振动器的振动频率相同,故C正确;
D.振动器对不同树干作用结束后,树干振动频率为其固有频率,所以树干的自由振动频率不一定相同,故D错误。
故选C。
5.D
【解析】
【分析】
【详解】
A.自由摆动的秋千摆动幅度越来越小,说明秋千的机械能越来越小,机械能不守恒。故A错误;
BD.秋千的机械能越来越小,减小的机械能转化为内能。能量并没有消失。故B错误,D正确;
C.秋千的机械能越来越小,减小的机械能转化为内能,并不仅仅是动能与重力势能之间的转化。故C错误。
故选D。
6.C
【解析】
【分析】
【详解】
部队过桥时如齐步走,给桥梁施加周期性外力,容易使桥的振动幅度增加,即发生共振,造成桥梁倒塌;登山运动员登高山时高声叫喊,声波容易引发雪山共振而发生雪崩,所以C正确;ABD错误;
故选C。
7.B
【解析】
【详解】
A.驱动力的频率越接近汽车的固有频率,颠簸越厉害,A错误;
BCD.汽车以约8m/s的速度行驶时,驱动力的周期为
驱动力的频率为
汽车做受迫振动的振动频率为4Hz,恰好等于汽车的固有频率,汽车发生共振,振幅最大,颠簸最厉害,B正确,CD错误。
故选B。
8.B
【解析】
【分析】
【详解】
A.阻尼振动的周期不变,振幅减小,故A错误;
BC.由于阻力影响,单摆要克服阻力做功,在运动过程中机械能一直逐渐减小,故P时刻的机械能大于N时刻的机械能,而两点重力势能相等,则P时刻的动能大于N时刻的动能,故B正确,C错误;
D.因为PN两时刻位置关于平衡位置对称,但是速度不等,则两时刻受到绳子的拉力大小不相等,故D错误;
故选B。
9.D
【解析】
【分析】
【详解】
AB.受迫振动的频率与驱动力的周期相同,所以弹簧振子的振动周期为,则AB错误;
CD.发生共振时,物体振动的振幅最大,共振的条件是驱动力的频率等于物体的固有频率,根据
所以要使弹簧振子的振幅增大,可让把手的转速增大,则C错误;D正确;
故选D。
10.B
【解析】
【分析】
【详解】
支架在受到竖直方向且频率为9 Hz的驱动力作用下做受迫振动时,频率越接近则振幅越大,所以甲的振幅较大。受迫振动的频率取决于驱动力的频率即振动频率为9 Hz。
故选B。
11.B
【解析】
【分析】
【详解】
在靠近塔杆悬点处加挂一个小锤,是为了减弱输电线振动的幅度,减缓输电线因周期性的弯折发生破坏。
故选B。
12.B
【解析】
【分析】
【详解】
停止对大钟的撞击后,大钟的振动不会立即停止,振动的能量不会凭空消失,它会再振动一段时间然后因为阻尼而停止,因此还会在空气中形成声波,这就是余音未绝的原因。
故选B。
13.A
【解析】
【分析】
【详解】
发生共振的条件是驱动力的频率等于物体的固有频率,而酒杯的固有频率为500;可知“狮子吼”的频率接近500,所以“狮子吼”的波长
故选A。
14.D
【解析】
【详解】
A.弹簧振子做简谐振动时,振动系统的机械能守恒,势能和动能之和保持不变,故A正确;
B.单摆做简谐振动的周期与摆球质量无关,所以质量增大后周期不变,故B正确;
C.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,故C正确;
D.弹簧振子的振动方程为
只要知道A、ω和这三个物理量我们便可以确定振子在任意时刻的位置以及速度的方向,而振子初始时刻的位置对应于,周期对应于ω,由于仅根据无法确定A和,所以已知弹簧振子初始时刻的位置及其振动周期,无法确定振子在任意时刻运动速度的方向,故D错误。
故选D。
15.C
【解析】
【分析】
【详解】
当驱动力的频率等于弹簧振子的故有频率时,振幅最大,所以当把手转动的频率逐渐缓慢增大时,当频率达到4Hz时,振幅最大,大于4Hz后再增大,振幅又减小,即弹簧振子的振动先越来越剧烈再越来越弱。
故选C。
16. 80 4800
【解析】
【分析】
【详解】
[1]当驱动力的频率等于钢片的固有频率时,将发生共振,振幅最大,所以发动机的转动的频率等于钢片的振动频率,即
[2]所以发动机的转速
17. 阻尼振动 0.25 0.33
【解析】
【分析】
【详解】
[1]当圆盘转动一会静止后,小球受阻力作用而做阻尼振动;
[2]若弹簧和小球构成的系统振动频率约为3Hz,现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定,小球的振动频率等于驱动力的频率,即为;
[3]逐渐改变圆盘的转动周期,当小球振动的振幅达到最大时,此时圆盘的周期等于小球的固有周期,即为。
18.正确
【解析】
【分析】
【详解】
物体做受迫振动时,其振动频率等于驱动力的频率,与固有频率无关
19.(1)简谐运动,0.5s,2Hz,阻尼振动;(2)受迫振动,0.25 s;(3)2 r/s,见解析
【解析】
【分析】
【详解】
(1)用手往下拉振子使振子获得一定能量,放手后,振子因所受回复力与位移成正比,方向与位移方向相反(F=-kx),所以做简谐运动,其周期和频率是由它本身的结构性质决定的,称固有周期(T固)和固有频率(f固),根据题意
T固==s=0.5 s
f固==Hz=2 Hz
由于摩擦力和空气阻力的存在,振子克服摩擦力和阻力做功消耗能量,使其振幅越来越小,故振动为阻尼振动。
(2)由于把手转动的转速为4 r/s,它给弹簧振子的驱动力频率为f驱=4 Hz,周期T驱=0.25 s,故振子做受迫振动。振动达稳定状态后,其频率(或周期)等于驱动力的频率(或周期),而跟固有频率(或周期)无关。即f=f驱=4 Hz,T=T驱=0.25 s。
(3)要使弹簧振子的振幅最大,处于共振状态,必须使其驱动力的频率f驱等于它的固有频率f固,即f驱=f固=2 Hz,故把手的转速应为n=2 r/s。
20.见解析
【解析】
【分析】
【详解】
高层建筑在大风中摇晃这是比较正常的现象,建筑物越高,迎风面积越大,那么其在大风中摇晃的程度就会越高。总高达632m的上海中心也不能避免,但它在多方面的设计都考虑了地震和大风导致的摆动,做了相应的抗震与抗风设计,将这个晃动效应减到了最低;
这个主阻尼器的总质量达到了1000吨。安装位置是在距离地面584米,位于126层的大楼顶部,上千吨的物体在大楼顶部会头重脚轻吗?其实这样理解就错了,第一跟大楼的质量相比,这1000吨并不是什么严重问题,因为设计时就已经考虑,另一层面,减轻晃动,放在大楼底部,左侧无重物阻尼时晃动是难以控制的,而右侧有重物阻尼晃动明显减轻,并且还是主动阻尼。
21.(1)1.58m;(2)左移
【解析】
【详解】
(1)由图可知,当驱动力的频率等于0.4Hz时,单摆达到共振,此时该摆的周期为T=2.5s;
则根据周期公式可知
代入数据解得
l=1.58m
(2)若摆长变大,则周期变大,固有频率减小,则共振曲线的峰值将左移。
22.5.33m/s
【解析】
【详解】
汽车做受迫振动,经过相邻的凸起所用的时间为受迫振动的周期,根据共振的条件
T固=T驱=1.5 s
时振动最剧烈,所以汽车速度为
答案第1页,共2页
答案第1页,共2页
一、单选题
1.正在运转的机器,当其飞轮以角速度匀速转动时,机器的振动不强烈,切断电源,飞轮的转动逐渐慢下来,在某一小段时间内机器却发生了强烈的振动,此后飞轮转速继续变慢,机器的振动也随之减弱,在机器停下来之后若重新启动机器,使飞轮转动的角速度从0较缓慢地增大到,在这一过程中( )
A.机器一定不会发生强烈的振动
B.机器不一定还会发生强烈的振动
C.若机器发生强烈振动,强烈振动可能发生在飞轮角速度为时
D.若机器发生强烈振动,强烈振动时飞轮的角速度肯定不为
2.下列说法正确的是( )
A.在同一地点,单摆做简谐振动的周期与其摆长成正比
B.弹簧振子做简谐振动时,振动系统的势能与动能之和逐渐减少
C.弹簧振子做简谐振动时,弹簧的劲度系数越大,单摆做简谐振动的周期越大
D.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率
3.如图所示为CCTV10“我爱发明”节目中介绍的松果采摘机,松果采摘机利用机械臂抱紧树干,通过采摘振动头振动而摇动树干,使得松果脱落。下列说法正确是( )
A.工作中,树干的振动频率小于采摘振动头的振动频率
B.采摘振动头振动频率越高,采摘落果的效果一定越好
C.采摘振动头振动频率减小,树干的振动幅度可能增大
D.若采摘振动头停止振动,树干的振动频率会逐渐减小
4.松子以其独特的香味、丰富的植物脂肪含量,成为了坚果界的宠儿。在我国东北地区,为了提高采摘效率,工程技术人员发明了振动器,将振动器固定在树干上,如图所示,机车带动振动器振动,使松果落下。则( )
A.针对不同树干,落果效果最好时的振动频率相同
B.随着振动器频率的增加,树干振动的幅度一定增大
C.振动器正常工作时,不同树干的振动频率始终与振动器的振动频率相同
D.振动器对不同树干作用结束后,树干的自由振动频率相同
5.自由摆动的秋千摆动幅度越来越小,下列说法正确的是( )
A.机械能守恒 B.能量正在消失
C.只有动能和势能相互转化 D.减少的机械能转化为内能
6.部队经过桥梁时,规定不许齐步走,登山运动员登雪山时,不许高声叫喊,主要原因是( )
A.减轻对桥的压力,避免产生回声
B.减少对桥、雪山的冲击力
C.避免使桥发生共振和使雪山发生共振
D.使桥受到的压力更不均匀,使登山运动员耗散能量
7.为了交通安全,常在公路上设置如图所示的减速带,减速带使路面稍微拱起以达到使车辆减速的目的。一排等间距设置的减速带,可有效降低车速。如果某路面上的减速带间距为2m,一辆固有频率为4Hz的汽车匀速驶过这排减速带,下列说法正确的是( )
A.汽车速度越大,颠簸一定越厉害
B.汽车以约8m/s的速度行驶时颠簸最厉害
C.汽车以约8m/s的速度行驶时颠簸最轻
D.汽车以10m/s的速度行驶时,其振动频率为4Hz
8.如图所示是某单摆做阻尼振动的振动图线,下列说法正确的是( )
A.振动过程中周期变小
B.摆球P时刻的机械能大于N时刻的机械能
C.摆球P时刻的动能等于N时刻的动能
D.小球在P时刻和N时刻,受到绳子拉力的大小相等
9.如图所示的装置,在曲轴上悬挂一个弹簧振子,若不转动把手,让其自由振动,周期为。现使把手以周期匀速转动(),当其运行到稳定后,则( )
A.弹簧振子的振动周期为
B.弹簧振子的振动周期为
C.要使弹簧振子的振幅增大,可让把手的转速减小
D.要使弹簧振子的振幅增大,可让把手的转速增大
10.如图所示,把两个弹簧振子悬挂在同一支架上,已知甲弹簧振子的固有频率为8 Hz,乙弹簧振子的固有频率为72 Hz,当支架在受到竖直方向且频率为9 Hz的驱动力作用下做受迫振动时,两个弹簧振子的振动情况是( )
A.甲的振幅较大,且振动频率为8 Hz
B.甲的振幅较大,且振动频率为9 Hz
C.乙的振幅较大,且振动频率为9 Hz
D.乙的振幅较大,且振动频率为72 Hz
11.高压输电线路塔杆较高,杆距较大,当输电线受到风吹动时,会发生较强烈的振动,输电线会因周期性的弯折发生破坏,为此,需要在靠近塔杆悬点处加挂一个小锤,如图所示。下列说法正确的是( )
A.小锤的作用是防雷电
B.小锤的作用是为了减弱输电线振动的幅度
C.小锤的振动与输电线振动是同步的
D.小锤的规格与杆距无关
12.在敲响古刹里的大钟时,有的同学发现,停止对大钟的撞击后,大钟仍“余音未绝”,分析其原因是( )
A.大钟的回声 B.大钟在继续振动
C.人的听觉发生“暂留”的缘故 D.大钟虽停止振动,但空气仍在振动
13.在喜剧电影《功夫》中,包租婆的“狮子吼”可以将酒杯震碎。若我们用手指轻弹同样的酒杯,听到清脆的声音,并测得该声音的频率为500,已知空气中的声速为340,则包租婆的“狮子吼”声波的波长约为( )
A.0.68m B.1.32m C.1.47m D.2.94m
14.下列说法不正确的是( )
A.弹簧振子做简谐振动时,振动系统的势能与动能之和保持不变
B.在同一地点,当摆长不变时,摆球质量越大,单摆做简谐振动的周期不变
C.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率
D.已知弹簧振子初始时刻的位置及其振动周期,就可知振子在任意时刻运动速度的方向
15.如图所示的装置,弹簧振子的固有频率是。现匀速转动把手,给弹簧振子以周期性的驱动力,测得弹簧振子振动达到稳定时的频率为,则把手转动的频率逐渐缓慢增大时,下列说法中正确的是( )
A.弹簧振子的振动越来越剧烈
B.弹簧振子的振动越来越弱
C.弹簧振子的振动先越来越剧烈再越来越弱
D.弹簧振子的振动先越来越弱再越来越剧烈
二、填空题
16.如图所示是用来测量各种发动机转速的转速计原理图。在同一铁支架上焊有固有频率依次为、80Hz、60Hz、40Hz的四个钢片将端与正在转动的电动机接触,发现钢片振幅最大,则此时振动频率为____________,电动机转速为___________。
17.如图所示,一个竖直圆盘转动时,固定在圆盘上的小圆柱带动一个T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球组成的振动系统,小球浸没在水中;当圆盘转动一会静止后,小球做____振动(选填“阻尼”,“自由”,“受迫”);若弹簧和小球构成的系统振动频率约为3Hz,现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定,小球的振动频率为_____Hz;逐渐改变圆盘的转动周期,当小球振动的振幅达到最大时,此时圆盘的周期为____s。
18.判断该说法的正误:
物体做受迫振动时,其振动频率与固有频率无关。( )
三、解答题
19.如图所示,在曲轴A上悬挂一个弹簧振子,如果转动把手,曲轴可以带动弹簧振子上下振动。问:
(1)开始时不转动把手,而用手往下拉振子,然后放手让振子上下振动,测得振子在10 s内完成20次全振动,振子做什么振动?其固有周期和固有频率各是多少?若考虑摩擦和空气阻力,振子做什么振动?
(2)在振子正常振动过程中,以转速4r/s匀速转动把手,振子的振动稳定后,振子做什么运动?其周期是多少?
(3)若要振子振动的振幅最大,把手的转速应多大?为什么?
20.上海中心大厦高632m,上面安装有重达1000t的风阻尼器。请查阅相关资料,了解它的作用及工作原理。
21.如图所示是一个单摆的共振曲线。
(1)试估计此单摆的摆长;(g取)
(2)若摆长增大,共振曲线的峰将怎样移动?
22.汽车的车身是装在弹簧上的,如果这个系统的固有周期是1.5 s,汽车在一条起伏不平的路上行驶,路上各凸起处大约都相隔8 m,汽车以多大速度行驶时,车身上下颠簸得最剧烈?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
【详解】
当驱动力频率等于系统的固有频率时会产生共振,飞轮在转速逐渐减小的过程中,机器出现强烈的振动,说明发生共振现象,此时飞轮转动的频率等于机器本身的固有频率;当机器重新启动时,飞轮转速缓慢增大的过程中,一旦达到共振条件,机器一定还会发生强烈的振动.由题意可知,发生强烈共振时,飞轮的角速度一定小于ω0。
故选D。
2.D
【解析】
【分析】
【详解】
A.根据单摆的周期公式
分析知,在同一地点,单摆做简谐振动的周期的平方与其摆长成正比,A错误;
B.弹簧振子做简谐振动时,只有重力或弹簧的弹力做功,振动系统的势能与动能之和保持不变,B错误;
C.根据弹簧振子的周期公式
可知弹簧的劲度系数越大,弹簧振子做简谐振动的周期越小,C错误;
D.根据受迫振动的特点可知,系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,D正确。
故选D。
3.C
【解析】
【详解】
A.受迫振动的频率等于驱动力频率,工作中,树干的振动频率等于采摘振动头的振动频率,故A错误;
BC.当采摘振动头振动频率等于树干的固有频率时,将发生共振现象,此时树干的振幅最大,采摘落果的效果最好,若开始时采摘振动头振动频率大于树干的固有频率,则增大频率后,树干的振幅反而减小,采摘落果的效果更差,而此时若减小采摘振动头振动频率,则树干的振幅会增大,故B错误,C正确;
D.若采摘振动头停止振动,树干的振动频率不变,振幅逐渐减小,故D错误。
故选C。
4.C
【解析】
【详解】
A.不同的树干,固有频率可能不同,根据共振的产生条件,针对不同树干,落果效果最好时的振动频率可能不相同,故A错误;
B.只有振动器的频率与树干的固有频率相同时,树干振动的幅度最大,所以随着振动器频率的增加,树干振动的幅度不一定增大,故B错误;
C.树干在振动器的振动下,做受迫振动,所以振动器正常工作时,不同树干的振动频率始终与振动器的振动频率相同,故C正确;
D.振动器对不同树干作用结束后,树干振动频率为其固有频率,所以树干的自由振动频率不一定相同,故D错误。
故选C。
5.D
【解析】
【分析】
【详解】
A.自由摆动的秋千摆动幅度越来越小,说明秋千的机械能越来越小,机械能不守恒。故A错误;
BD.秋千的机械能越来越小,减小的机械能转化为内能。能量并没有消失。故B错误,D正确;
C.秋千的机械能越来越小,减小的机械能转化为内能,并不仅仅是动能与重力势能之间的转化。故C错误。
故选D。
6.C
【解析】
【分析】
【详解】
部队过桥时如齐步走,给桥梁施加周期性外力,容易使桥的振动幅度增加,即发生共振,造成桥梁倒塌;登山运动员登高山时高声叫喊,声波容易引发雪山共振而发生雪崩,所以C正确;ABD错误;
故选C。
7.B
【解析】
【详解】
A.驱动力的频率越接近汽车的固有频率,颠簸越厉害,A错误;
BCD.汽车以约8m/s的速度行驶时,驱动力的周期为
驱动力的频率为
汽车做受迫振动的振动频率为4Hz,恰好等于汽车的固有频率,汽车发生共振,振幅最大,颠簸最厉害,B正确,CD错误。
故选B。
8.B
【解析】
【分析】
【详解】
A.阻尼振动的周期不变,振幅减小,故A错误;
BC.由于阻力影响,单摆要克服阻力做功,在运动过程中机械能一直逐渐减小,故P时刻的机械能大于N时刻的机械能,而两点重力势能相等,则P时刻的动能大于N时刻的动能,故B正确,C错误;
D.因为PN两时刻位置关于平衡位置对称,但是速度不等,则两时刻受到绳子的拉力大小不相等,故D错误;
故选B。
9.D
【解析】
【分析】
【详解】
AB.受迫振动的频率与驱动力的周期相同,所以弹簧振子的振动周期为,则AB错误;
CD.发生共振时,物体振动的振幅最大,共振的条件是驱动力的频率等于物体的固有频率,根据
所以要使弹簧振子的振幅增大,可让把手的转速增大,则C错误;D正确;
故选D。
10.B
【解析】
【分析】
【详解】
支架在受到竖直方向且频率为9 Hz的驱动力作用下做受迫振动时,频率越接近则振幅越大,所以甲的振幅较大。受迫振动的频率取决于驱动力的频率即振动频率为9 Hz。
故选B。
11.B
【解析】
【分析】
【详解】
在靠近塔杆悬点处加挂一个小锤,是为了减弱输电线振动的幅度,减缓输电线因周期性的弯折发生破坏。
故选B。
12.B
【解析】
【分析】
【详解】
停止对大钟的撞击后,大钟的振动不会立即停止,振动的能量不会凭空消失,它会再振动一段时间然后因为阻尼而停止,因此还会在空气中形成声波,这就是余音未绝的原因。
故选B。
13.A
【解析】
【分析】
【详解】
发生共振的条件是驱动力的频率等于物体的固有频率,而酒杯的固有频率为500;可知“狮子吼”的频率接近500,所以“狮子吼”的波长
故选A。
14.D
【解析】
【详解】
A.弹簧振子做简谐振动时,振动系统的机械能守恒,势能和动能之和保持不变,故A正确;
B.单摆做简谐振动的周期与摆球质量无关,所以质量增大后周期不变,故B正确;
C.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,故C正确;
D.弹簧振子的振动方程为
只要知道A、ω和这三个物理量我们便可以确定振子在任意时刻的位置以及速度的方向,而振子初始时刻的位置对应于,周期对应于ω,由于仅根据无法确定A和,所以已知弹簧振子初始时刻的位置及其振动周期,无法确定振子在任意时刻运动速度的方向,故D错误。
故选D。
15.C
【解析】
【分析】
【详解】
当驱动力的频率等于弹簧振子的故有频率时,振幅最大,所以当把手转动的频率逐渐缓慢增大时,当频率达到4Hz时,振幅最大,大于4Hz后再增大,振幅又减小,即弹簧振子的振动先越来越剧烈再越来越弱。
故选C。
16. 80 4800
【解析】
【分析】
【详解】
[1]当驱动力的频率等于钢片的固有频率时,将发生共振,振幅最大,所以发动机的转动的频率等于钢片的振动频率,即
[2]所以发动机的转速
17. 阻尼振动 0.25 0.33
【解析】
【分析】
【详解】
[1]当圆盘转动一会静止后,小球受阻力作用而做阻尼振动;
[2]若弹簧和小球构成的系统振动频率约为3Hz,现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定,小球的振动频率等于驱动力的频率,即为;
[3]逐渐改变圆盘的转动周期,当小球振动的振幅达到最大时,此时圆盘的周期等于小球的固有周期,即为。
18.正确
【解析】
【分析】
【详解】
物体做受迫振动时,其振动频率等于驱动力的频率,与固有频率无关
19.(1)简谐运动,0.5s,2Hz,阻尼振动;(2)受迫振动,0.25 s;(3)2 r/s,见解析
【解析】
【分析】
【详解】
(1)用手往下拉振子使振子获得一定能量,放手后,振子因所受回复力与位移成正比,方向与位移方向相反(F=-kx),所以做简谐运动,其周期和频率是由它本身的结构性质决定的,称固有周期(T固)和固有频率(f固),根据题意
T固==s=0.5 s
f固==Hz=2 Hz
由于摩擦力和空气阻力的存在,振子克服摩擦力和阻力做功消耗能量,使其振幅越来越小,故振动为阻尼振动。
(2)由于把手转动的转速为4 r/s,它给弹簧振子的驱动力频率为f驱=4 Hz,周期T驱=0.25 s,故振子做受迫振动。振动达稳定状态后,其频率(或周期)等于驱动力的频率(或周期),而跟固有频率(或周期)无关。即f=f驱=4 Hz,T=T驱=0.25 s。
(3)要使弹簧振子的振幅最大,处于共振状态,必须使其驱动力的频率f驱等于它的固有频率f固,即f驱=f固=2 Hz,故把手的转速应为n=2 r/s。
20.见解析
【解析】
【分析】
【详解】
高层建筑在大风中摇晃这是比较正常的现象,建筑物越高,迎风面积越大,那么其在大风中摇晃的程度就会越高。总高达632m的上海中心也不能避免,但它在多方面的设计都考虑了地震和大风导致的摆动,做了相应的抗震与抗风设计,将这个晃动效应减到了最低;
这个主阻尼器的总质量达到了1000吨。安装位置是在距离地面584米,位于126层的大楼顶部,上千吨的物体在大楼顶部会头重脚轻吗?其实这样理解就错了,第一跟大楼的质量相比,这1000吨并不是什么严重问题,因为设计时就已经考虑,另一层面,减轻晃动,放在大楼底部,左侧无重物阻尼时晃动是难以控制的,而右侧有重物阻尼晃动明显减轻,并且还是主动阻尼。
21.(1)1.58m;(2)左移
【解析】
【详解】
(1)由图可知,当驱动力的频率等于0.4Hz时,单摆达到共振,此时该摆的周期为T=2.5s;
则根据周期公式可知
代入数据解得
l=1.58m
(2)若摆长变大,则周期变大,固有频率减小,则共振曲线的峰值将左移。
22.5.33m/s
【解析】
【详解】
汽车做受迫振动,经过相邻的凸起所用的时间为受迫振动的周期,根据共振的条件
T固=T驱=1.5 s
时振动最剧烈,所以汽车速度为
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
