第二章 整式的加减的复习
图片预览






文档简介
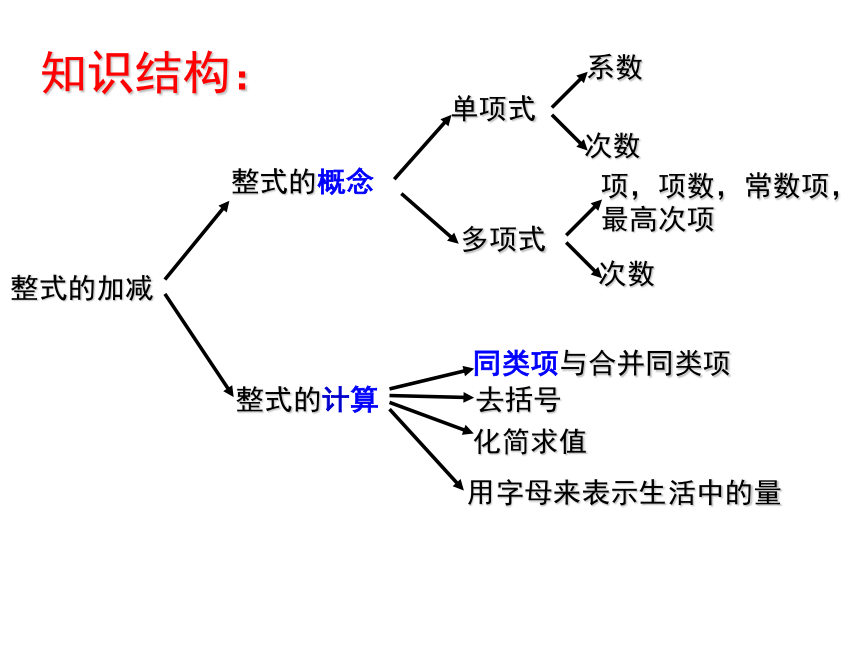
课件20张PPT。第二章 整式的加减复习南门学校 七年(3)(4)青春的美好并不在于年轻、时尚、好玩,而在于青春充满希望。知识结构:整式的加减整式的概念整式的计算单项式多项式系数次数项,项数,常数项,最高次项次数同类项与合并同类项去括号化简求值用字母来表示生活中的量定义:单项式中的_________。次数:1.当单项式的系数是1或-1时,“1”通常省略不写。单项式:系数:数字或字母的乘积由_________________组成的式子。
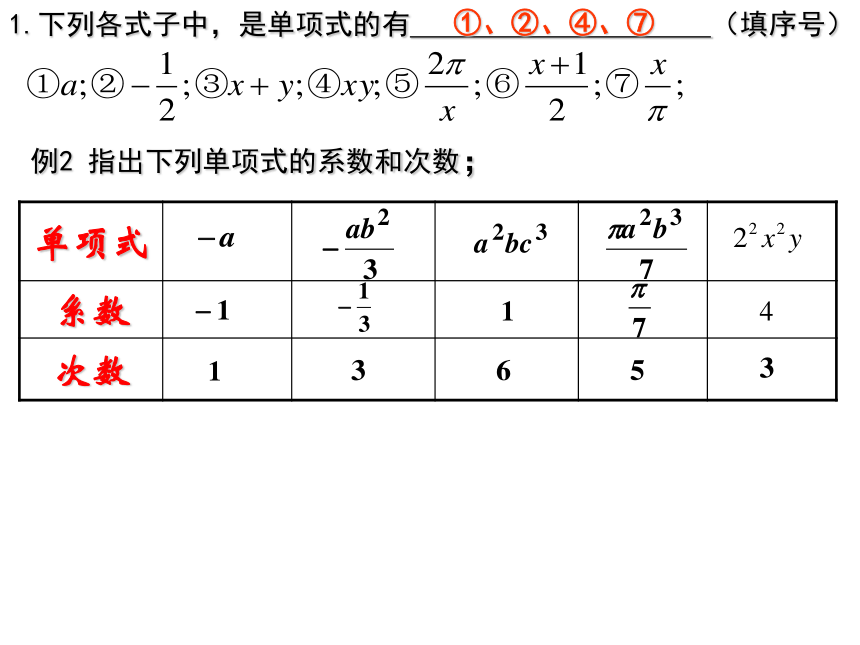
单独的______或________也是单项式。单项式中的__________________.数字因数所有字母的指数和一个数一个字母注意的问题:2.当式子分母中出现字母时不是单项式。3.圆周率π是常数,不要看成字母。4.当单项式的系数是带分数时,通常写成假分数。5.单项式的系数应包括它前面的性质符号。6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。7.单独的数字不含字母, 规定它的次数是零次.1.下列各式子中,是单项式的有 (填序号)①、②、④、⑦例2 指出下列单项式的系数和次数;定义:几个__________.常数项:多项式中_______________.多项式的次数:_________________________.
项: 组成多项式中的_____________.
有几项,就叫做_________.1.在确定多项式的项时,要连同它前面的符号,
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。多项式单项式的和每一个单项式几项式不含字母的项多项式中次数最高的项的次数。注意的问题:1.下列多项式次数为3的是( )C2.请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;注意(1)多项式的次数不是所有项的次数的和,而是它的最高 次项次数;
(2)多项式的每一项都包含它前面的符号;
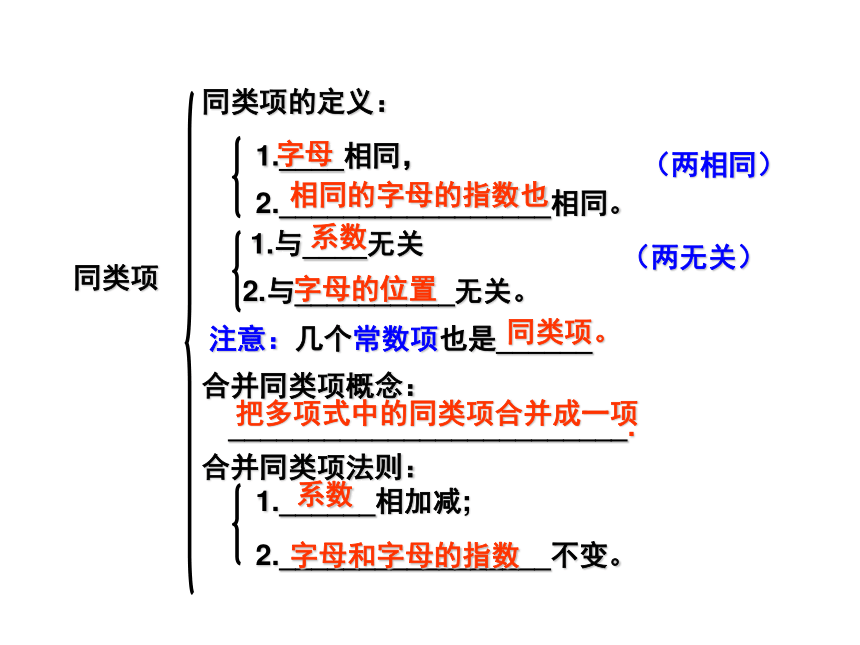
(3)再强调一次, “π”当作数字,而不是字母同类项的定义:(两相同)合并同类项概念:_________________________.合并同类项法则:2._________________不变。2._________________相同。1.____相同,字母相同的字母的指数也1.______相加减;字母和字母的指数系数同类项注意:几个常数项也是______同类项。(两无关)2.与__________无关。1.与____无关系数 字母的位置把多项式中的同类项合并成一项⑤ 与 ④ 与 ③ 与 ② 与 ① 与 2.若 与 是同类项,则m+n=___. 1.下列各式中,是同类项的是:_ _ ⑥-125 与4. 判断下列各题是否正确,对打√,错打×
(1)2x+5y=7y ( ) (2)6ab-ab=6 ( )
(3)8x3y-9xy3=x3y ( ) (4) m3-2m3= ( )
(5)5ab+4c=9abc ( ) (6)3x3+2x2=5x5 ( )
(7)4x2+x2=5x2 ( ) (8)3a2b-7ab2=-4ab ( )6.化简: 6x2y+2xy-3x2y2-7x-5yx-4y2x2-6x2y ③ ⑤ ⑥5×××××××√解原式=-3xy-7x2y2-7x3.若 与 的和是一个单项式,则 =___.45.若 ,则m+n-p=______-4-16整式的加减混合运算步骤(有括号先去括号)1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.利用乘法分配律计算结果。
4.按要求按“升”或“降”幂排列。找放算排1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去括号,看符号。是‘+’号,不变号,是‘-’号,全变号”一:去括号二:计算(按照先小括号,再中括号,最后大括号的顺序)1.判断下列各式是否正确:√××( )( )( )×( )2. 下列各个式子中,书写格式正确的是( )1、代数式中用到乘法时,若是数字与数字乘,要用“×” 若是数字与字母乘,乘号通常写成”.”或省略不写,如 3×y应写成3·y或3y,且数字与字母相乘时,字母与字母相乘,乘号通常写成“·”或省略不写。
2、带分数与字母相乘,要写成假分数.
3、代数式中出现除法运算时,一般用分数写,即用分数线代替除号。
4、系数一般写在字母的前面,且系数“1”往往会省略;F例3 合并同类项:小明的解法:(1)错在把所有项都当作同类项了;正确的解法:小明的解法:(2)错在把结合同类项时弄错了符号;正确的解法:总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。1.去掉下列各式中的括号。(1)8m-(3n+5)(2)n-4(3-2m)(3)2(a-2b)-3(2m-n)=8m-3n-5=n-12+8m=2a-4b-6m+3n2.化简:-(3x-2y+z)-[5x-(x-2y+z)-3x]-4x3.求当x= 时,多项式的值。解:原式===把x= 带入 中,得 ∴ 原式=54.当x=1时, 则当x=-1时,解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7=-5-2解:原式====6.如果关于x,y的多项式 的差
不含有二次项,求 的值。解:原式=由题意知,则: m-3=0
2+2n=07、化简下列各式: 9、把下列各式填入相应的集合中: 单项式集合{ …};
多项式集合{ …};
整式集合{ … }.B11.已知a2+ab=-3,ab+b2=7,试求a2+2ab+b2;a2-b2的值。12. 评析:对含有两个或两个以上字母的多项式重新排列,先要确定是按哪个字母升(降)幂排列,再将常数项或不含这个字母的项按照升幂排在第一项,降幂排在最后一项。(1)按x的升幂排列;(2)按y的降幂排列。解:(1)按x的升幂排列:(2)按y的降幂排列:13.当a = -2,b = -1,c = 0.5时,
求:2abc -{a2b -[3abc -(4ab2 -a2b)]}的值.14.多项式 如果的次数为4次,则m为多少?如果多项式只有二项,则m为多少?15.已知x2+x+3=8,求3x2+3x-6的值
变式:已知x2+x+3=8,求-x2-x+8的值, 10x2+10x-10的值,你会变式?
16.已知:当x=-2时,多项式ax5+bx3+cx-1的值为5. 求当x=2时,这个多项式的值.17.如果A是5次多项式,B也是5次多项式,那么A+B一定是( )(A)10次多项式。(B)次数不低于5次的多项式。(C)5次多项式。(D)次数不高于5次的整式。18.关于x的多项式
的值与x无关.
(1)求ab的值;
(2)求代数式 的值.计算:(1)
(2)
(3)
(4)整 式 的 加 减 单项式:多项式:去括号:同类项:合并同类项:整式的加减:定义、系数、次数定义、项、次数、常数项定义、“两相同、两无关”定义、法则法 则整 式步 骤重点结 束 寄 语不经历风雨,怎能见彩虹!再 见
单独的______或________也是单项式。单项式中的__________________.数字因数所有字母的指数和一个数一个字母注意的问题:2.当式子分母中出现字母时不是单项式。3.圆周率π是常数,不要看成字母。4.当单项式的系数是带分数时,通常写成假分数。5.单项式的系数应包括它前面的性质符号。6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。7.单独的数字不含字母, 规定它的次数是零次.1.下列各式子中,是单项式的有 (填序号)①、②、④、⑦例2 指出下列单项式的系数和次数;定义:几个__________.常数项:多项式中_______________.多项式的次数:_________________________.
项: 组成多项式中的_____________.
有几项,就叫做_________.1.在确定多项式的项时,要连同它前面的符号,
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。多项式单项式的和每一个单项式几项式不含字母的项多项式中次数最高的项的次数。注意的问题:1.下列多项式次数为3的是( )C2.请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;注意(1)多项式的次数不是所有项的次数的和,而是它的最高 次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母同类项的定义:(两相同)合并同类项概念:_________________________.合并同类项法则:2._________________不变。2._________________相同。1.____相同,字母相同的字母的指数也1.______相加减;字母和字母的指数系数同类项注意:几个常数项也是______同类项。(两无关)2.与__________无关。1.与____无关系数 字母的位置把多项式中的同类项合并成一项⑤ 与 ④ 与 ③ 与 ② 与 ① 与 2.若 与 是同类项,则m+n=___. 1.下列各式中,是同类项的是:_ _ ⑥-125 与4. 判断下列各题是否正确,对打√,错打×
(1)2x+5y=7y ( ) (2)6ab-ab=6 ( )
(3)8x3y-9xy3=x3y ( ) (4) m3-2m3= ( )
(5)5ab+4c=9abc ( ) (6)3x3+2x2=5x5 ( )
(7)4x2+x2=5x2 ( ) (8)3a2b-7ab2=-4ab ( )6.化简: 6x2y+2xy-3x2y2-7x-5yx-4y2x2-6x2y ③ ⑤ ⑥5×××××××√解原式=-3xy-7x2y2-7x3.若 与 的和是一个单项式,则 =___.45.若 ,则m+n-p=______-4-16整式的加减混合运算步骤(有括号先去括号)1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.利用乘法分配律计算结果。
4.按要求按“升”或“降”幂排列。找放算排1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去括号,看符号。是‘+’号,不变号,是‘-’号,全变号”一:去括号二:计算(按照先小括号,再中括号,最后大括号的顺序)1.判断下列各式是否正确:√××( )( )( )×( )2. 下列各个式子中,书写格式正确的是( )1、代数式中用到乘法时,若是数字与数字乘,要用“×” 若是数字与字母乘,乘号通常写成”.”或省略不写,如 3×y应写成3·y或3y,且数字与字母相乘时,字母与字母相乘,乘号通常写成“·”或省略不写。
2、带分数与字母相乘,要写成假分数.
3、代数式中出现除法运算时,一般用分数写,即用分数线代替除号。
4、系数一般写在字母的前面,且系数“1”往往会省略;F例3 合并同类项:小明的解法:(1)错在把所有项都当作同类项了;正确的解法:小明的解法:(2)错在把结合同类项时弄错了符号;正确的解法:总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。1.去掉下列各式中的括号。(1)8m-(3n+5)(2)n-4(3-2m)(3)2(a-2b)-3(2m-n)=8m-3n-5=n-12+8m=2a-4b-6m+3n2.化简:-(3x-2y+z)-[5x-(x-2y+z)-3x]-4x3.求当x= 时,多项式的值。解:原式===把x= 带入 中,得 ∴ 原式=54.当x=1时, 则当x=-1时,解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7=-5-2解:原式====6.如果关于x,y的多项式 的差
不含有二次项,求 的值。解:原式=由题意知,则: m-3=0
2+2n=07、化简下列各式: 9、把下列各式填入相应的集合中: 单项式集合{ …};
多项式集合{ …};
整式集合{ … }.B11.已知a2+ab=-3,ab+b2=7,试求a2+2ab+b2;a2-b2的值。12. 评析:对含有两个或两个以上字母的多项式重新排列,先要确定是按哪个字母升(降)幂排列,再将常数项或不含这个字母的项按照升幂排在第一项,降幂排在最后一项。(1)按x的升幂排列;(2)按y的降幂排列。解:(1)按x的升幂排列:(2)按y的降幂排列:13.当a = -2,b = -1,c = 0.5时,
求:2abc -{a2b -[3abc -(4ab2 -a2b)]}的值.14.多项式 如果的次数为4次,则m为多少?如果多项式只有二项,则m为多少?15.已知x2+x+3=8,求3x2+3x-6的值
变式:已知x2+x+3=8,求-x2-x+8的值, 10x2+10x-10的值,你会变式?
16.已知:当x=-2时,多项式ax5+bx3+cx-1的值为5. 求当x=2时,这个多项式的值.17.如果A是5次多项式,B也是5次多项式,那么A+B一定是( )(A)10次多项式。(B)次数不低于5次的多项式。(C)5次多项式。(D)次数不高于5次的整式。18.关于x的多项式
的值与x无关.
(1)求ab的值;
(2)求代数式 的值.计算:(1)
(2)
(3)
(4)整 式 的 加 减 单项式:多项式:去括号:同类项:合并同类项:整式的加减:定义、系数、次数定义、项、次数、常数项定义、“两相同、两无关”定义、法则法 则整 式步 骤重点结 束 寄 语不经历风雨,怎能见彩虹!再 见
