圆心角与圆周角的关系(1)
图片预览




文档简介
课件20张PPT。第三节 圆周角和圆心角的关系(一)第三章 圆回顾与思考
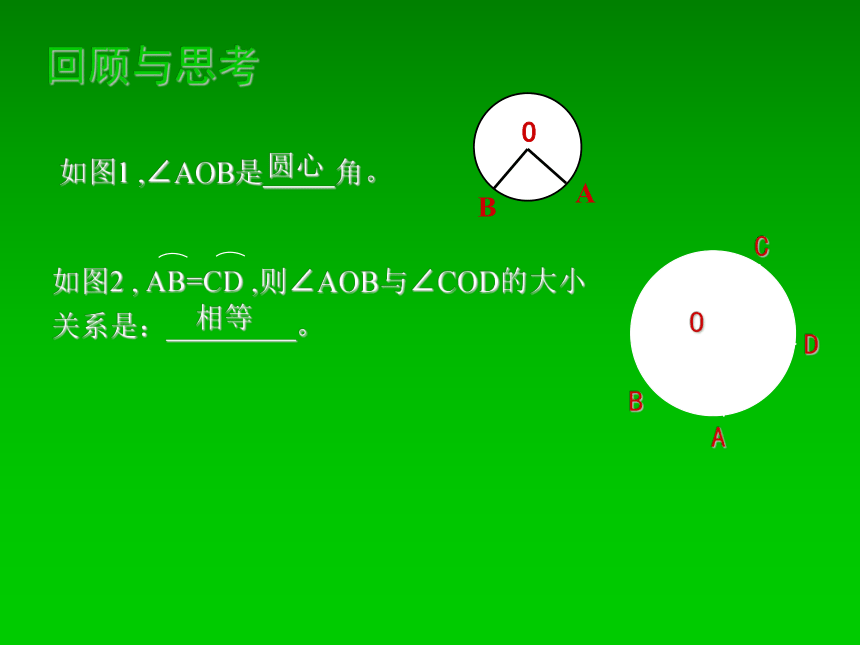
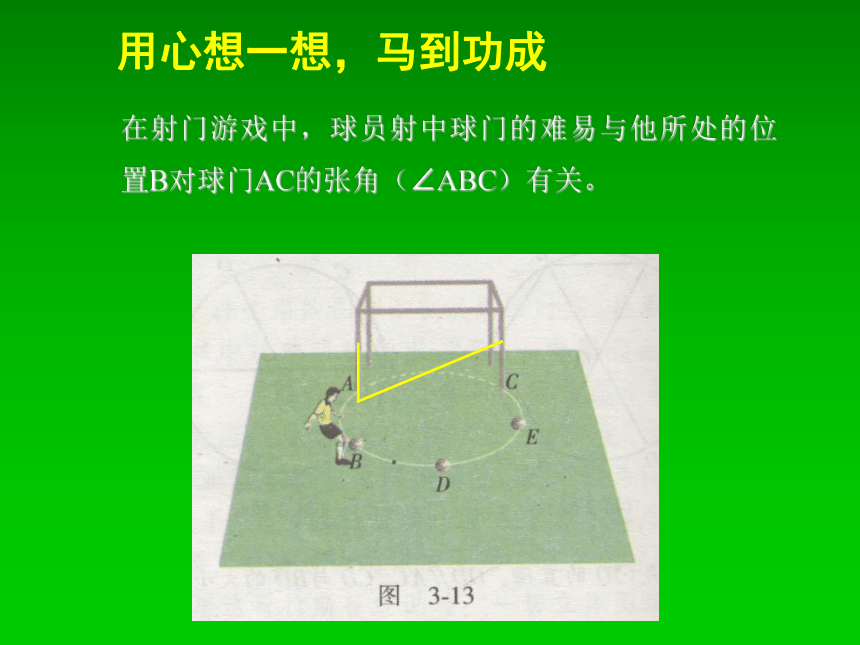
如图1 ,∠AOB是 角。如图2 , AB=CD ,则∠AOB与∠COD的大小关系是: 。BAOCD圆心相等用心想一想,马到功成在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角(∠ABC)有关。
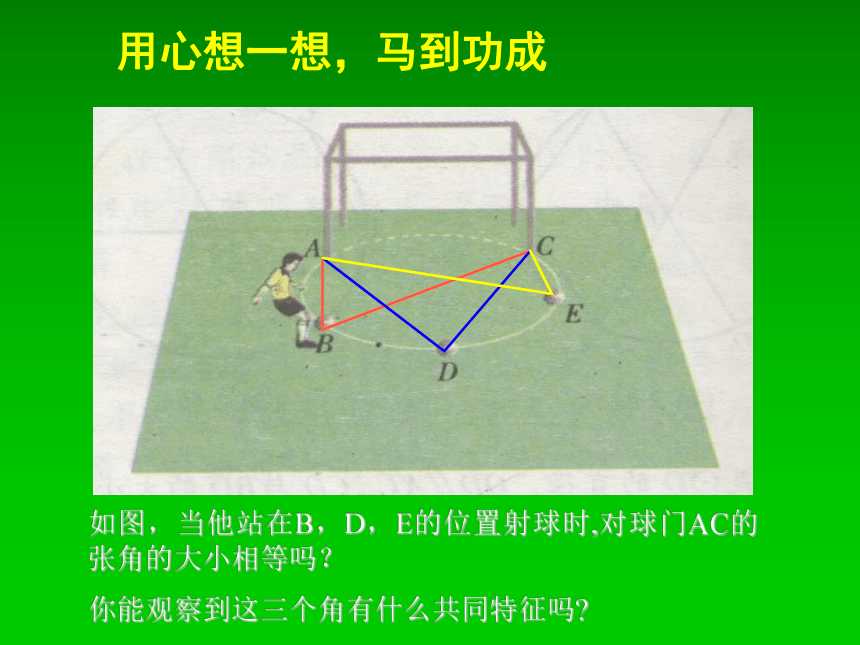
用心想一想,马到功成如图,当他站在B,D,E的位置射球时,对球门AC的张角的大小相等吗?你能观察到这三个角有什么共同特征吗?用心想一想,马到功成为解决这个问题我们先来研究一种角。
观察图中的∠ABC,顶点在什么位置?角的两边有什么特点?用心想一想,马到功成观察图中的∠ABC,可以发现,它的顶点在圆上,它的两边分别与圆还有另一个交点。像这样的角,叫做圆周角。请同学们思考:如果一个角是圆周角,这个角有何特点?圆周角有两个特征:
①角的顶点在圆上;
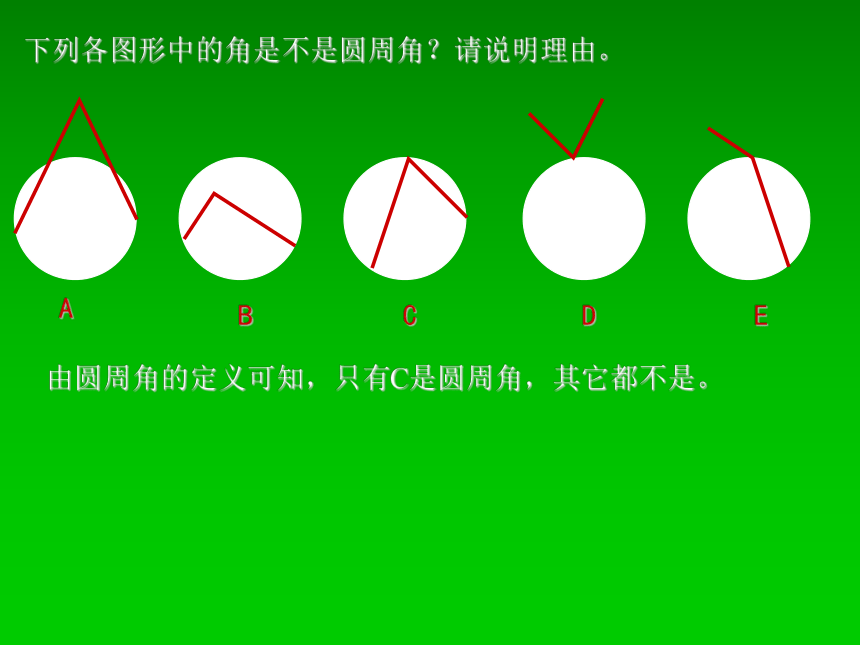
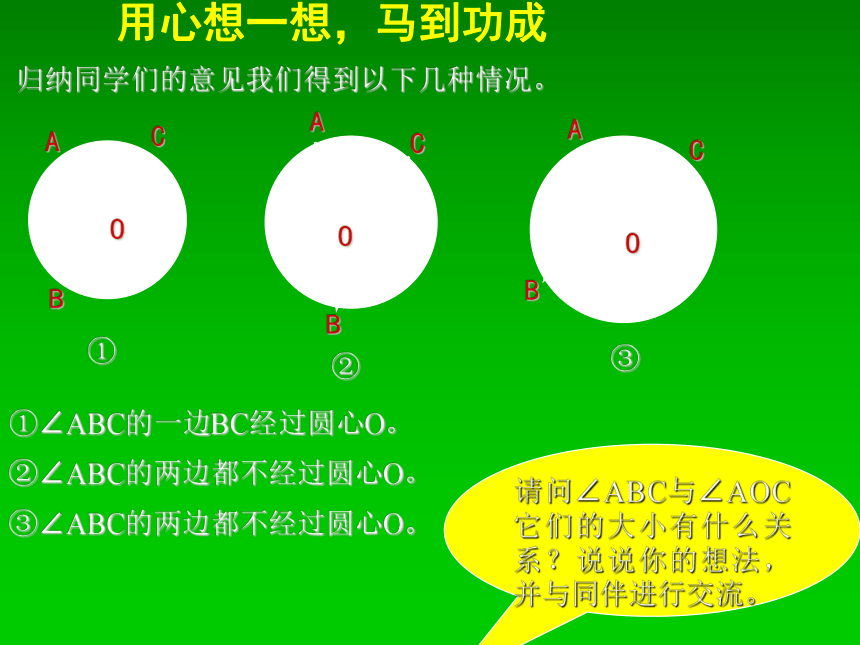
②两边在圆内的部分是圆的两条弦。下列各图形中的角是不是圆周角?请说明理由。ABCDE由圆周角的定义可知,只有C是圆周角,其它都不是。用心想一想,马到功成我们再来研究圆周角的性质。为了解决这个问题,我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系。请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。用心想一想,马到功成归纳同学们的意见我们得到以下几种情况。①∠ABC的一边BC经过圆心O。②∠ABC的两边都不经过圆心O。③∠ABC的两边都不经过圆心O。请问∠ABC与∠AOC它们的大小有什么关系?说说你的想法,并与同伴进行交流。下面我们首先考虑同学们列举的一种特殊情况,即∠ABC的一边BC经过圆心O。∵ ∠AOC是△ABO的外角,∴ ∠AOC=∠ABO+∠BAO。∵ OA=OB,∴ ∠ABO=∠BAO。∴ ∠AOC=2∠ABO,如图,我们可以观察到∠AOC是△ABO的外角,∠ABC是△ABO的一个内角,它们两者存在一定关系.
下面我们首先考虑同学们列举的一种特殊情况,即∠ABC的一边BC经过圆心O。∵ ∠AOC是△ABO的外角,∴ ∠AOC=∠ABO+∠BAO。∵ OA=OB,∴ ∠ABO=∠BAO。∴ ∠AOC=2∠ABO,那么当∠ABC的两边都不经过圆心O时,∠ABC与∠AOC又有怎样的大小关系呢?我们可以考虑把这两种情况分别转化成刚才的特殊情形来考虑。也就是借用直径,连接BO并延长,与圆相交于点D。D(此时我们得到与图①同样的情形)如图,连接BO并延长,与圆相交于点D。(此时我们得到与图①同样的情形)D如图,连接BO并延长,与相交于点D。(此时我们得到与图①同样的情形)D如图,连接BO并延长,与相交于点D。(此时我们得到与图①同样的情形)D认真观察,探求结果通过对三种情形的证明,同学们再认真观察图形,你会得到什么结果?一条弧所对的圆周角等于它所对的圆心角的 。一半一题多变如图,在⊙O中,∠BOC=50°,
则∠BAC= 。25° 一题多变如图,在⊙O中,∠BOC=50°,
则∠BAC= 。变化题2:如图,∠BAC=40°,则∠OBC= 。变化题1:如图,点A,B,C是⊙O上的三点, ∠BAC=40°,则∠BOC= 。 25° 50° 80° 由∠BAC=40°可得∠BOC=80°,再由△BOC是等腰三角形可求得∠OBC。课内拓展延伸1.到目前为止,我们学习到和圆有关的角有几个?它们各有什么特点?相互之间有什么关系?答:和圆有关的角有圆心角和圆周角.圆心角顶点在圆心;圆周角顶点在圆上,角的两边和圆相交。一条弧所对的圆周角等于它所对的圆心角的一半。谢谢合作!
如图1 ,∠AOB是 角。如图2 , AB=CD ,则∠AOB与∠COD的大小关系是: 。BAOCD圆心相等用心想一想,马到功成在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角(∠ABC)有关。
用心想一想,马到功成如图,当他站在B,D,E的位置射球时,对球门AC的张角的大小相等吗?你能观察到这三个角有什么共同特征吗?用心想一想,马到功成为解决这个问题我们先来研究一种角。
观察图中的∠ABC,顶点在什么位置?角的两边有什么特点?用心想一想,马到功成观察图中的∠ABC,可以发现,它的顶点在圆上,它的两边分别与圆还有另一个交点。像这样的角,叫做圆周角。请同学们思考:如果一个角是圆周角,这个角有何特点?圆周角有两个特征:
①角的顶点在圆上;
②两边在圆内的部分是圆的两条弦。下列各图形中的角是不是圆周角?请说明理由。ABCDE由圆周角的定义可知,只有C是圆周角,其它都不是。用心想一想,马到功成我们再来研究圆周角的性质。为了解决这个问题,我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系。请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。用心想一想,马到功成归纳同学们的意见我们得到以下几种情况。①∠ABC的一边BC经过圆心O。②∠ABC的两边都不经过圆心O。③∠ABC的两边都不经过圆心O。请问∠ABC与∠AOC它们的大小有什么关系?说说你的想法,并与同伴进行交流。下面我们首先考虑同学们列举的一种特殊情况,即∠ABC的一边BC经过圆心O。∵ ∠AOC是△ABO的外角,∴ ∠AOC=∠ABO+∠BAO。∵ OA=OB,∴ ∠ABO=∠BAO。∴ ∠AOC=2∠ABO,如图,我们可以观察到∠AOC是△ABO的外角,∠ABC是△ABO的一个内角,它们两者存在一定关系.
下面我们首先考虑同学们列举的一种特殊情况,即∠ABC的一边BC经过圆心O。∵ ∠AOC是△ABO的外角,∴ ∠AOC=∠ABO+∠BAO。∵ OA=OB,∴ ∠ABO=∠BAO。∴ ∠AOC=2∠ABO,那么当∠ABC的两边都不经过圆心O时,∠ABC与∠AOC又有怎样的大小关系呢?我们可以考虑把这两种情况分别转化成刚才的特殊情形来考虑。也就是借用直径,连接BO并延长,与圆相交于点D。D(此时我们得到与图①同样的情形)如图,连接BO并延长,与圆相交于点D。(此时我们得到与图①同样的情形)D如图,连接BO并延长,与相交于点D。(此时我们得到与图①同样的情形)D如图,连接BO并延长,与相交于点D。(此时我们得到与图①同样的情形)D认真观察,探求结果通过对三种情形的证明,同学们再认真观察图形,你会得到什么结果?一条弧所对的圆周角等于它所对的圆心角的 。一半一题多变如图,在⊙O中,∠BOC=50°,
则∠BAC= 。25° 一题多变如图,在⊙O中,∠BOC=50°,
则∠BAC= 。变化题2:如图,∠BAC=40°,则∠OBC= 。变化题1:如图,点A,B,C是⊙O上的三点, ∠BAC=40°,则∠BOC= 。 25° 50° 80° 由∠BAC=40°可得∠BOC=80°,再由△BOC是等腰三角形可求得∠OBC。课内拓展延伸1.到目前为止,我们学习到和圆有关的角有几个?它们各有什么特点?相互之间有什么关系?答:和圆有关的角有圆心角和圆周角.圆心角顶点在圆心;圆周角顶点在圆上,角的两边和圆相交。一条弧所对的圆周角等于它所对的圆心角的一半。谢谢合作!
