沪科版八年级下册19.4 综合与实践 多边形的镶嵌 教案
文档属性
| 名称 | 沪科版八年级下册19.4 综合与实践 多边形的镶嵌 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 617.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览



文档简介
沪科版 19.4 综合与实践 多边形的镶嵌
教学设计
教学目标
1.了解平面图形镶嵌的含义,掌握哪些平面图形可以镶嵌,镶嵌的理由及简单的镶嵌设计.
2.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌,并能运用这几种图形进行简单的设计.
3.经历探索多边形镶嵌的过程,进一步发展学生的合情推理能力,开发、培养学生创造性思维.培养学生动手操作,自主探索,合作学习的能力.
4.使学生进一步体会平面图形在现实生活中的广泛应用,体会数学与现实生活的密切联系,认识数学的应用价值.
内容分析
从数学的角度看,用形状和大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺:通常把这类问题画做用多边形的平面镶嵌.平面图形的镶嵌内容安排在本章的最后,在此之前,学生已经学习了三角形的内角和,多边形的内角和等知识.通过这个课题的学习,学生可以经历从实际问题抽象出数学问题,建立数学模型,综合应用已有知识解决问题的过程,从而加深对相关知识的理解,提高思维能力,获得分析问题的方法,对于今后的学习具有重要的意义.
教学重点难点
教学重点
探索正多边形能够镶嵌的条件.
教学难点
通过数学实验发现用正多边形进行镶嵌的规律.
数学思考
1.通过用一种正多边形进行镶嵌的实验,探究平面镶嵌的条件.
2.探究用哪两种不同的正多边形可以进行组合镶嵌.
3.用三角形与四边形能否进行平面镶嵌.
问题解决
获得一些研究问题的方法和经验,发展思维能力,加深理解相关的数学知识.
教学过程
一、情境引入 赏镶嵌之美
1.图形欣赏.
多媒体出示一组图片,让学生观察欣赏,
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
引导学生思考:这些图案都是由哪些基本的平面图形构成的?这些图形拼成一个平面有什么共同特征?
说明:图案中的平面图形有的规则,有的不规则;有的用多边形拼成,有的用多种多边形拼成.各图形之间没有空隙,边也没有重叠.
设计意图:一方面让学生直观感受各种图形,特别是蜂窝的图学生都比较熟悉,体现了自然中、游戏中都蕴含着美妙的数学知识,激发学生学习的兴趣,另一方面使学生体会镶嵌的直观形象,进而明确其含义.
2.感知概念
平面镶嵌的定义
用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
二、动手操作 合作学习
1.提出问题.
(1)怎样铺设可以不留空隙,也不相互重叠?
(2)可以用哪些图形?
(3)用前面所学的正多边形能否拼成一个平面图形?
(4)哪些正多边形可以镶嵌成一个平面,哪些不能?
设计意图:恰当设计问题,使学生的认识由感性上升到理性,培养学生的合情推理能力,领会镶嵌的原理,进一步培养学生的思维能力,发挥教师的引导者和合作者的作用.
2.操作发现 寻镶嵌之理
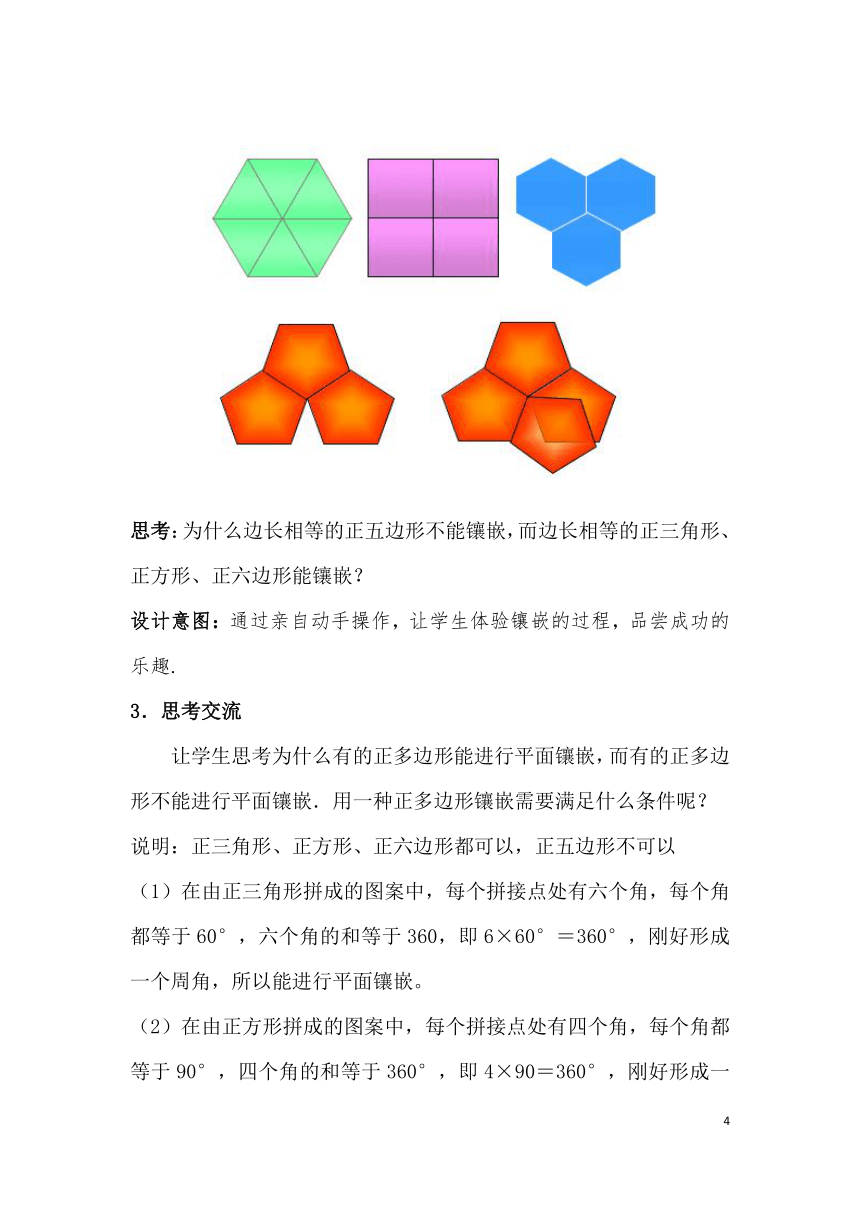
让学生先用课前准备好的若干正三角形、正方形、正五边形、正六边形进行拼图游戏.教师巡视,观察学生的活动,共同展示交流.
思考:为什么边长相等的正五边形不能镶嵌,而边长相等的正三角形、正方形、正六边形能镶嵌?
设计意图:通过亲自动手操作,让学生体验镶嵌的过程,品尝成功的乐趣.
3.思考交流
让学生思考为什么有的正多边形能进行平面镶嵌,而有的正多边形不能进行平面镶嵌.用一种正多边形镶嵌需要满足什么条件呢?
说明:正三角形、正方形、正六边形都可以,正五边形不可以
(1)在由正三角形拼成的图案中,每个拼接点处有六个角,每个角都等于60°,六个角的和等于360,即6×60°=360°,刚好形成一个周角,所以能进行平面镶嵌。
(2)在由正方形拼成的图案中,每个拼接点处有四个角,每个角都等于90°,四个角的和等于360°,即4×90=360°,刚好形成一个周角,所以能进行平面镶嵌。
(3)在由正六边形拼成的图案中,每个拼接点处有三个角每个角都等于120°,三个角的和等于360°,即3×120=360°,刚好形成一个周角,所以能进行平面镶嵌。
(4)在由正五边形拼成的图案中,每个拼接点处有三个角,每个角都等于108°,三个角的和等于324°,即3×108=324°,不能形成一个周角,所以不能进行平面镶嵌。
4.得出结论
操作发现
实验结果 正n边形 拼图 每个内角的度数 多边形个 数 结果
n=3
n=4
n=6
n=5
你得到的结论是:_________________________
(1)正三角形、正方形、正六边形能够用来作平面镶嵌,正五边形不能用来作平面镶嵌.
(2)用一种正多边形进行平面镶嵌,则这个正多边形的内角度数能整除360°.
(3)除了正三角形、正方形、正六边形之外,其他任意的正多边形都不能用来作平面镶嵌,这是因为其他任意正多边形在顶点处的几个内角都不能拼成一个周角.
5.延伸拓展
思考:如果用一种多边形进行平面镶嵌时不采用正多边形而改为任意多边形,有没有这样的多边形?为什么?
学生思考,尝试.教师注意适时引导.
结论:除了上面几种正多边形可以用来作平面镶嵌外,任意的三角形和四边形也可以用来作平面镶嵌.但若想实现连续铺设,还应将相等的边重合在一起.
理由:三角形、四边形的内角和均能整除360°.
三、拓展探究 创设美丽镶嵌图案
思考:你能同时应用两种正多边形进行平面镶嵌吗?
学生思考操作,教师引导,最后展示交流,明确镶嵌的原理.
设计意图:用理论作为依据,训练学生分析回题、解决问题,自主探究学习的能力.探究多种组合,体会理论来源于实践,用理论又能指导实践的研究问题的方法.
四、牛刀小试
现有边长相等的正三角形、正方形和正六边形纸片若干张,下列拼法中不能镶嵌成一个平面图案的是( )
A.正三角形和正六边形
B.正三角形和正方形
C正方形和正六边形
D.正三角形、正方形和正六边形
四、课堂小结
通过本节课的学习你学到了哪些知识?你最大的收获是什么?
平面镶嵌的条件:
(1)当围绕一点的几个正多边形的内角和为360°时,就能拼成一个平面图形.
(2)用同一种正多边形镶嵌平面的条件是:当正多边形的内角的正整数倍是360°时,这种正多边形可以覆盖平面,只有正三角形、正方形和正六边形三种.
(3)用两种边长相等的正多边形镶嵌平面的条件是:拼接在同一个点的各个角的和恰好等于360°(周角).
(4)在一般的多边形中,只有三角形和四边形可以覆盖平面.
设计意图:通过交流总结让学生用数学知识来解释生活现象,体会数学的奇妙,再次激发学生学习数学的热情.
五、布置作业 用美见证收获
1.请你分别按下列要求设计一个多边形的镶嵌图案
(1)只用一种正多边形;
(2)同时用两种正多边形;
(3)用一种非正多边形.
2.某校要用地砖镶嵌艺术教室的地面,可以选择的方案有许多种,请你为其设计:
(1) 如果在以下形状的地传中选取一种镶嵌地面,可以选择的有_________.(填
序号)
①正方形;
②正五边形;
③正六边形;
④正八边形;
⑤任意三角形;
⑥任意四边形.
(2)如果在正三角形、正方形、正八边形这三形状的地砖中,任意选取其中的两种,有儿种可行的方案
(3)如果在正三角形、正方形、正六边形、正二边形这四种形状的地砖中,任意选取其中的三种,有几种可行的方案
板书设计
19.4 多边形的镶嵌
1.平面镶嵌的定义;
2.平面镶嵌的条件;
3.生活中的平面镶嵌.‘
教学反思:
1. 学生动手操作与交流活动,符合学生的认知规律.明白了密铺原理
此节课,学生动手环节一步一个脚印,难度逐步上升,符合学生的认知规律.首先选择一种形状、大小完全相同的正多边形进行密铺,展示作品后让学生思考、交流,归纳出平面镶嵌的原理:若选择同一种正多边形进行密铺,在一个拼接点处有n个角,这些角的和应为360°,之后从边长相等的等边三角形、正方形、正六边形和正八边形中选出两种合适的正多边形进行密铺,从一种图形上升到两种图形,难度上升,从特殊到一般,将结论进行推广:若平面图形能够进行密铺,则在一个拼接点处的所有角的和应为360°,最后更为一般,用形状大小完全相同的任意三角形或任意四边形进行密,再一次验证了密铺的原理.此活动虽为老师设计,但仍然可以让学生体会到研究问题从特殊到一般、从易到难的研究过程,学生在动手操作的同时,归纳结论,动脑思考,自己归纳出相应的结论,效果比老师讲授的知识要印象深刻的多,这样的数学实践课应该属高效课堂.
2. 欣赏经典的密铺图案,体会了数学的文化价值
平面镶嵌是数学之美中典型的例子、体现了直观之美。此环节老师若再增加一些生活中的图片,以及世界各国数学家对某些多边形密铺的研究,让学生感受浓厚的的数学文化色移,则能更加激发学生学学习数学的热情.
3.学生自主参与、积极主动,才能有更生动的课堂
我们知道,课堂上,民主的教学氮围,教师鼓励学生的自主性,容许学生在自行探索中去发现知识,容许学生表达不同意见,学习活动较为自由,这种教育环境,有利于培养学生的创造性,本节课的做法正符合这些要求,值得推崇.若该数学实验课上,学生能更多的自主参与,积极而主动,将会极大地提高课堂的效率.在教学过程中,课堂教学形式生动,学生作为活动的主体,手脑并用,以“做”为支架的活动方式,有利于发现数学结论,理解数学知识,验证数学猜想.
4.触发学生火热的思考,走出教室,仍然面对问号,怀抱好奇
荷兰数学家弗赖登塔尔提出:学习数学唯一正确的方法是实行“再创造”,也就是由学生本人把要学的东西自己发现或创造出来.数学实践课堂上,学生虽然真正地“动”了起来、学习热情高涨,但时间相当有限,往往发现的都是较为浅显的结论,并不能通过45分钟发现更深的结论,所以要兼顾实际情况,在课后让学生积极探索,继续研究,触发学生火热的思考,这样学生学习数学的兴趣也会大大提升,渐渐进人一个良性循环的状态.
2
教学设计
教学目标
1.了解平面图形镶嵌的含义,掌握哪些平面图形可以镶嵌,镶嵌的理由及简单的镶嵌设计.
2.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌,并能运用这几种图形进行简单的设计.
3.经历探索多边形镶嵌的过程,进一步发展学生的合情推理能力,开发、培养学生创造性思维.培养学生动手操作,自主探索,合作学习的能力.
4.使学生进一步体会平面图形在现实生活中的广泛应用,体会数学与现实生活的密切联系,认识数学的应用价值.
内容分析
从数学的角度看,用形状和大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺:通常把这类问题画做用多边形的平面镶嵌.平面图形的镶嵌内容安排在本章的最后,在此之前,学生已经学习了三角形的内角和,多边形的内角和等知识.通过这个课题的学习,学生可以经历从实际问题抽象出数学问题,建立数学模型,综合应用已有知识解决问题的过程,从而加深对相关知识的理解,提高思维能力,获得分析问题的方法,对于今后的学习具有重要的意义.
教学重点难点
教学重点
探索正多边形能够镶嵌的条件.
教学难点
通过数学实验发现用正多边形进行镶嵌的规律.
数学思考
1.通过用一种正多边形进行镶嵌的实验,探究平面镶嵌的条件.
2.探究用哪两种不同的正多边形可以进行组合镶嵌.
3.用三角形与四边形能否进行平面镶嵌.
问题解决
获得一些研究问题的方法和经验,发展思维能力,加深理解相关的数学知识.
教学过程
一、情境引入 赏镶嵌之美
1.图形欣赏.
多媒体出示一组图片,让学生观察欣赏,
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
引导学生思考:这些图案都是由哪些基本的平面图形构成的?这些图形拼成一个平面有什么共同特征?
说明:图案中的平面图形有的规则,有的不规则;有的用多边形拼成,有的用多种多边形拼成.各图形之间没有空隙,边也没有重叠.
设计意图:一方面让学生直观感受各种图形,特别是蜂窝的图学生都比较熟悉,体现了自然中、游戏中都蕴含着美妙的数学知识,激发学生学习的兴趣,另一方面使学生体会镶嵌的直观形象,进而明确其含义.
2.感知概念
平面镶嵌的定义
用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
二、动手操作 合作学习
1.提出问题.
(1)怎样铺设可以不留空隙,也不相互重叠?
(2)可以用哪些图形?
(3)用前面所学的正多边形能否拼成一个平面图形?
(4)哪些正多边形可以镶嵌成一个平面,哪些不能?
设计意图:恰当设计问题,使学生的认识由感性上升到理性,培养学生的合情推理能力,领会镶嵌的原理,进一步培养学生的思维能力,发挥教师的引导者和合作者的作用.
2.操作发现 寻镶嵌之理
让学生先用课前准备好的若干正三角形、正方形、正五边形、正六边形进行拼图游戏.教师巡视,观察学生的活动,共同展示交流.
思考:为什么边长相等的正五边形不能镶嵌,而边长相等的正三角形、正方形、正六边形能镶嵌?
设计意图:通过亲自动手操作,让学生体验镶嵌的过程,品尝成功的乐趣.
3.思考交流
让学生思考为什么有的正多边形能进行平面镶嵌,而有的正多边形不能进行平面镶嵌.用一种正多边形镶嵌需要满足什么条件呢?
说明:正三角形、正方形、正六边形都可以,正五边形不可以
(1)在由正三角形拼成的图案中,每个拼接点处有六个角,每个角都等于60°,六个角的和等于360,即6×60°=360°,刚好形成一个周角,所以能进行平面镶嵌。
(2)在由正方形拼成的图案中,每个拼接点处有四个角,每个角都等于90°,四个角的和等于360°,即4×90=360°,刚好形成一个周角,所以能进行平面镶嵌。
(3)在由正六边形拼成的图案中,每个拼接点处有三个角每个角都等于120°,三个角的和等于360°,即3×120=360°,刚好形成一个周角,所以能进行平面镶嵌。
(4)在由正五边形拼成的图案中,每个拼接点处有三个角,每个角都等于108°,三个角的和等于324°,即3×108=324°,不能形成一个周角,所以不能进行平面镶嵌。
4.得出结论
操作发现
实验结果 正n边形 拼图 每个内角的度数 多边形个 数 结果
n=3
n=4
n=6
n=5
你得到的结论是:_________________________
(1)正三角形、正方形、正六边形能够用来作平面镶嵌,正五边形不能用来作平面镶嵌.
(2)用一种正多边形进行平面镶嵌,则这个正多边形的内角度数能整除360°.
(3)除了正三角形、正方形、正六边形之外,其他任意的正多边形都不能用来作平面镶嵌,这是因为其他任意正多边形在顶点处的几个内角都不能拼成一个周角.
5.延伸拓展
思考:如果用一种多边形进行平面镶嵌时不采用正多边形而改为任意多边形,有没有这样的多边形?为什么?
学生思考,尝试.教师注意适时引导.
结论:除了上面几种正多边形可以用来作平面镶嵌外,任意的三角形和四边形也可以用来作平面镶嵌.但若想实现连续铺设,还应将相等的边重合在一起.
理由:三角形、四边形的内角和均能整除360°.
三、拓展探究 创设美丽镶嵌图案
思考:你能同时应用两种正多边形进行平面镶嵌吗?
学生思考操作,教师引导,最后展示交流,明确镶嵌的原理.
设计意图:用理论作为依据,训练学生分析回题、解决问题,自主探究学习的能力.探究多种组合,体会理论来源于实践,用理论又能指导实践的研究问题的方法.
四、牛刀小试
现有边长相等的正三角形、正方形和正六边形纸片若干张,下列拼法中不能镶嵌成一个平面图案的是( )
A.正三角形和正六边形
B.正三角形和正方形
C正方形和正六边形
D.正三角形、正方形和正六边形
四、课堂小结
通过本节课的学习你学到了哪些知识?你最大的收获是什么?
平面镶嵌的条件:
(1)当围绕一点的几个正多边形的内角和为360°时,就能拼成一个平面图形.
(2)用同一种正多边形镶嵌平面的条件是:当正多边形的内角的正整数倍是360°时,这种正多边形可以覆盖平面,只有正三角形、正方形和正六边形三种.
(3)用两种边长相等的正多边形镶嵌平面的条件是:拼接在同一个点的各个角的和恰好等于360°(周角).
(4)在一般的多边形中,只有三角形和四边形可以覆盖平面.
设计意图:通过交流总结让学生用数学知识来解释生活现象,体会数学的奇妙,再次激发学生学习数学的热情.
五、布置作业 用美见证收获
1.请你分别按下列要求设计一个多边形的镶嵌图案
(1)只用一种正多边形;
(2)同时用两种正多边形;
(3)用一种非正多边形.
2.某校要用地砖镶嵌艺术教室的地面,可以选择的方案有许多种,请你为其设计:
(1) 如果在以下形状的地传中选取一种镶嵌地面,可以选择的有_________.(填
序号)
①正方形;
②正五边形;
③正六边形;
④正八边形;
⑤任意三角形;
⑥任意四边形.
(2)如果在正三角形、正方形、正八边形这三形状的地砖中,任意选取其中的两种,有儿种可行的方案
(3)如果在正三角形、正方形、正六边形、正二边形这四种形状的地砖中,任意选取其中的三种,有几种可行的方案
板书设计
19.4 多边形的镶嵌
1.平面镶嵌的定义;
2.平面镶嵌的条件;
3.生活中的平面镶嵌.‘
教学反思:
1. 学生动手操作与交流活动,符合学生的认知规律.明白了密铺原理
此节课,学生动手环节一步一个脚印,难度逐步上升,符合学生的认知规律.首先选择一种形状、大小完全相同的正多边形进行密铺,展示作品后让学生思考、交流,归纳出平面镶嵌的原理:若选择同一种正多边形进行密铺,在一个拼接点处有n个角,这些角的和应为360°,之后从边长相等的等边三角形、正方形、正六边形和正八边形中选出两种合适的正多边形进行密铺,从一种图形上升到两种图形,难度上升,从特殊到一般,将结论进行推广:若平面图形能够进行密铺,则在一个拼接点处的所有角的和应为360°,最后更为一般,用形状大小完全相同的任意三角形或任意四边形进行密,再一次验证了密铺的原理.此活动虽为老师设计,但仍然可以让学生体会到研究问题从特殊到一般、从易到难的研究过程,学生在动手操作的同时,归纳结论,动脑思考,自己归纳出相应的结论,效果比老师讲授的知识要印象深刻的多,这样的数学实践课应该属高效课堂.
2. 欣赏经典的密铺图案,体会了数学的文化价值
平面镶嵌是数学之美中典型的例子、体现了直观之美。此环节老师若再增加一些生活中的图片,以及世界各国数学家对某些多边形密铺的研究,让学生感受浓厚的的数学文化色移,则能更加激发学生学学习数学的热情.
3.学生自主参与、积极主动,才能有更生动的课堂
我们知道,课堂上,民主的教学氮围,教师鼓励学生的自主性,容许学生在自行探索中去发现知识,容许学生表达不同意见,学习活动较为自由,这种教育环境,有利于培养学生的创造性,本节课的做法正符合这些要求,值得推崇.若该数学实验课上,学生能更多的自主参与,积极而主动,将会极大地提高课堂的效率.在教学过程中,课堂教学形式生动,学生作为活动的主体,手脑并用,以“做”为支架的活动方式,有利于发现数学结论,理解数学知识,验证数学猜想.
4.触发学生火热的思考,走出教室,仍然面对问号,怀抱好奇
荷兰数学家弗赖登塔尔提出:学习数学唯一正确的方法是实行“再创造”,也就是由学生本人把要学的东西自己发现或创造出来.数学实践课堂上,学生虽然真正地“动”了起来、学习热情高涨,但时间相当有限,往往发现的都是较为浅显的结论,并不能通过45分钟发现更深的结论,所以要兼顾实际情况,在课后让学生积极探索,继续研究,触发学生火热的思考,这样学生学习数学的兴趣也会大大提升,渐渐进人一个良性循环的状态.
2
