沪科版八年级下册20.2.1数据的集中趋势与离散程度-平均数教案
文档属性
| 名称 | 沪科版八年级下册20.2.1数据的集中趋势与离散程度-平均数教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 42.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览



文档简介
《20.2数据的集中趋势与离散程度》教学设计
第一课时 平均数
教材分析
平均数是在七年级学生学习了数据的收集与整理的基础上开展的。主要学习分析数据的集中趋势的常用方法,是数据处理与运用的进一步研究,是前面所学内容的深化。教材首先从学校空气含尘量这个熟悉的情景入手,提出平均数的概念和计算公式,通过例1感受平均数受极端值影响较大,并尝试解决方法。
教学目标
1.理解平均数是一组数据集中趋势的代表;
2.感受极端值对平均数的影响并积极寻求解决的策略;
3.学生经历运用平均数解决实际问题的过程,体验统计与生活的联系,养成用数据说话的习惯和实事求是的科学态度。
4.从学生对小学平均数的感性认识入手,到中学将平均数公式化的探究,在充满探索性的数学活动中感受知识螺旋上升带来的喜悦的同时渗透由特殊到一般的数学思想。
教学重难点
重点:灵活运用平均数解决实际问题。
难点:理解平均数为什么能作为一组数据集中趋势的代表。
教学过程
一、情境引入
展示空气污染的图片(PPT显示)
【设计意图】通过图片引入,激发学生的学习兴趣,同时向学生宣传环保意识,为下面引入空气含尘量的相关数据作铺垫.
二、探索新知
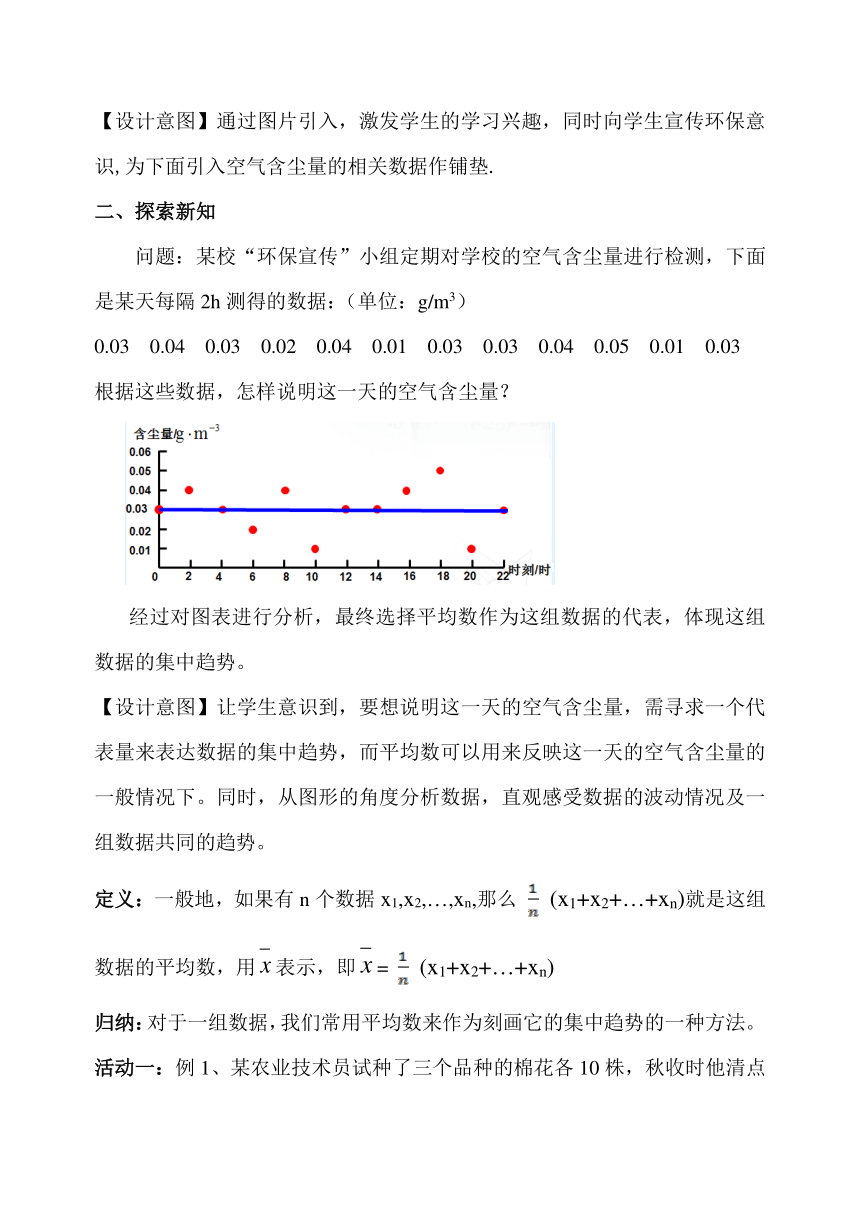
问题:某校“环保宣传”小组定期对学校的空气含尘量进行检测,下面是某天每隔2h测得的数据:(单位:g/m3)
0.03 0.04 0.03 0.02 0.04 0.01 0.03 0.03 0.04 0.05 0.01 0.03
根据这些数据,怎样说明这一天的空气含尘量?
经过对图表进行分析,最终选择平均数作为这组数据的代表,体现这组数据的集中趋势。
【设计意图】让学生意识到,要想说明这一天的空气含尘量,需寻求一个代表量来表达数据的集中趋势,而平均数可以用来反映这一天的空气含尘量的一般情况下。同时,从图形的角度分析数据,直观感受数据的波动情况及一组数据共同的趋势。
定义:一般地,如果有n个数据x1,x2,…,xn,那么 (x1+x2+…+xn)就是这组数据的平均数,用表示,即= (x1+x2+…+xn)
归纳:对于一组数据,我们常用平均数来作为刻画它的集中趋势的一种方法。
活动一:例1、某农业技术员试种了三个品种的棉花各10株,秋收时他清点了这30株棉花的结桃数如下表,请问哪个品种较好
甲种棉花 84,79,81,84,85,82,83,86,87,81
乙种棉花 85,84,89,79,81,91,79,76,82,84
丙种棉花 83,85,87,78,80,75,82,83,81,86
(1)想一想怎么样比较好
(比较这三种棉花的平均桃数就可能确定! )
(2)为什么比较平均桃数就能确定
(平均数可作为一组数据的数值的代表,要比较某些对象时,往往把这些对象有关数据的平均值进行比较.)
解:设甲、乙、丙三种棉花的平均数分别为:x甲 、x乙、x丙。
x甲=(84+79+81+84+85+82+83+86+87+81)
=83.5(个)
x乙=(85+84+89+79+81+91+79+76+82+84)
=83.0(个)
x丙=(83+85+87+78+80+75+82+83+81+86)
=82.0(个)
由于甲种棉花的平均结桃数高于其他两个品种棉花的结桃数,所以甲品种棉花较好。
思考:通过对上题的解决,你能说出平均数的大小与什么有关吗?
你能说出平均数的作用和特点吗?(学生交流回答,教师点评)
归纳:平均数的大小与一组数据的每个数据都有关系,如果这组数据中的一个数据变大,其平均数将变大;若这组数据中的一个数据变小,平均数将变小。平均数是一组数据的数值大小的集中代表值,它刻画了这组数据整体的平均状态,体现了这组数据的整体性质,对于这组数据的个体性质不能作出什么结论。
活动二:我们来解例2、例3
例2:在一次网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
1号 2号 3号 4号 5号 6号 7号 8号
甲 9.0 9.0 9.2 9.8 8.8 9.2 9.5 9.2
乙 9.4 9.6 9.2 8.0 9.5 9.0 9.2 9.4
你认为哪位选手会胜出?
分析:确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分;二是将评委评分中的一个最高分与一个最低分去掉后的平均数作为最后得分.哪种方案更可取?
解: 按方案一计算甲、乙的最后得分为:
x甲=(8.8+9.0×2+9.2×3+9.5+9.8)
≈9.21(分)
x乙=(8.0+9.0+9.2×2+9.4×2+9.6+9.5)
≈9.16(分)
这时候甲的成绩比乙高
按方案二计算甲、乙的最后得分
y甲=(9.0×2+9.2×3+9.5)
≈9.18(分)
y乙=(9.0+9.2×2+9.4×2+9.5)
≈9.28(分)
这时候乙的成绩比甲高。
结论:将上面的得分与表中的数据相比较,我们发现有5位评委对甲的评分不高于乙,这表明多数人认为乙的成绩比较好。方案二的结果表明乙的成绩比甲的高,与大多数评委的观点相符。因此,方案二评定选手的最后得分比较可取。
例3、个体户张某经营一家餐馆,下面是该餐馆所有工作人员2010年10月份的工资:
张某: 4000元; 会计: 700元; 厨师甲:1000元
厨师乙: 900元; 杂工甲:580元; 杂工乙:560元
服务员甲:620元;服务员乙:600元;服务员丙:580元
(1)计算他们的平均工资,这个平均工资能否反映餐馆员工在这个月收入的一般水平?
(2)不计张某的工资,再求餐馆员工的月平均工资,这个平均工资能代表一般水平吗?
解:(1)设餐馆全体员工的月平均工资为 x1 ,则:
x1=(4000+700+1000+900+580+560+620+600+580)
=1060(元)
(2)设8位员工的月平均工资为 x2 ,则:
x2=(700+1000+900+580+560+620+600+580)
=692.5(元)
结论:1060元不能代表餐馆员工在这个月的月收入的一般水平,因为员工中工资最高的厨师甲的月收入1000元也小于这个平均数。692.5元能代表餐馆员工在这个月的月收入的一般水平。
思考:通过这个问题,你能说出平均数有什么缺点吗?(学生回答,教师点评)
归纳:平均数的缺点:平均数的缺点是容易受个别特殊数据的影响。
想一想:怎样避免这个缺点?(学生讨论,教师点评)
为了消除这个缺点,当出现这种情形时,可以将特殊数据去掉。如某些评奖比赛的计分,通常去掉一个最高分和一个最低分。
三、课堂练习:
试一试:1、小明班上同学的平均身高是1.4米,小强班上同学的平均身高是1.45米,小明一定比小强矮吗?(指名学生回答)
(小明不一定比小强矮,平均数不能对个体特征作出描述。)
2、小王在学校举行的演讲比赛中,10位评委教师所打的分如下:9.6 , 9.5, 9.2 , 9.0,9.4,9.5 ,9.2, 9.3, 8.4, 9.7
你认为怎样计算小王的得分最合理?并求出你认为合理的分数?
学生活动:学生交流,解决,教师点评。(指名学生板演)
练一练:
1、一组数据:40、37、x、64的平均数是53,则x的值是( )
A、67 B、69 C、71 D、72
2、甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲 种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每 斤( )
A、3.88元 B、4.3元 C、8.7元 D、8.8元
3、某次考试A、B、C、D、E五名学生平均分为62分,除 A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、70 D、无法确定
4、某市的7月下旬最高气温统计如下:
气温 35度 34度 33度 32度 28度
天数 2 3 2 2 1
该市7月中旬最高气温的平均数是_____。
5、小明所在班级的男同学的平均体重是45kg,小亮所在班级的男同学的平均体重是42kg,则下列判断正确的是( )
A、小明体重是45kg B、小明比小亮重3kg
C、小明体重不能确定 D、小明与小亮体重相等
四、课堂小结
这节课我们学均数及平均数的计算公式,知道了平均数的计算公式和平均数的作用与特点及平均数的缺点 ,这对我们解决一些与平均数有关的问题将有所帮助。
五、课后作业:课本p135习题20.2 第1、2题
六、板书设计
(
2
0.2
数据的集中趋势与离散程度
――数据的集中趋势(第1课时)
1
、
一般地,如果有n个数据x
1
,x
2
,
…
,x
n
,,那么,
=
(x
1
+x
2
+
…
+x
n
)
2、意义:
3、极端值的影响
:
)
教学反思:
通过这节课的教学,我觉得学生对平均数的计算方法比较容易掌握,所以主要让学生理解过大或过小数据对平均数的影响。
第一课时 平均数
教材分析
平均数是在七年级学生学习了数据的收集与整理的基础上开展的。主要学习分析数据的集中趋势的常用方法,是数据处理与运用的进一步研究,是前面所学内容的深化。教材首先从学校空气含尘量这个熟悉的情景入手,提出平均数的概念和计算公式,通过例1感受平均数受极端值影响较大,并尝试解决方法。
教学目标
1.理解平均数是一组数据集中趋势的代表;
2.感受极端值对平均数的影响并积极寻求解决的策略;
3.学生经历运用平均数解决实际问题的过程,体验统计与生活的联系,养成用数据说话的习惯和实事求是的科学态度。
4.从学生对小学平均数的感性认识入手,到中学将平均数公式化的探究,在充满探索性的数学活动中感受知识螺旋上升带来的喜悦的同时渗透由特殊到一般的数学思想。
教学重难点
重点:灵活运用平均数解决实际问题。
难点:理解平均数为什么能作为一组数据集中趋势的代表。
教学过程
一、情境引入
展示空气污染的图片(PPT显示)
【设计意图】通过图片引入,激发学生的学习兴趣,同时向学生宣传环保意识,为下面引入空气含尘量的相关数据作铺垫.
二、探索新知
问题:某校“环保宣传”小组定期对学校的空气含尘量进行检测,下面是某天每隔2h测得的数据:(单位:g/m3)
0.03 0.04 0.03 0.02 0.04 0.01 0.03 0.03 0.04 0.05 0.01 0.03
根据这些数据,怎样说明这一天的空气含尘量?
经过对图表进行分析,最终选择平均数作为这组数据的代表,体现这组数据的集中趋势。
【设计意图】让学生意识到,要想说明这一天的空气含尘量,需寻求一个代表量来表达数据的集中趋势,而平均数可以用来反映这一天的空气含尘量的一般情况下。同时,从图形的角度分析数据,直观感受数据的波动情况及一组数据共同的趋势。
定义:一般地,如果有n个数据x1,x2,…,xn,那么 (x1+x2+…+xn)就是这组数据的平均数,用表示,即= (x1+x2+…+xn)
归纳:对于一组数据,我们常用平均数来作为刻画它的集中趋势的一种方法。
活动一:例1、某农业技术员试种了三个品种的棉花各10株,秋收时他清点了这30株棉花的结桃数如下表,请问哪个品种较好
甲种棉花 84,79,81,84,85,82,83,86,87,81
乙种棉花 85,84,89,79,81,91,79,76,82,84
丙种棉花 83,85,87,78,80,75,82,83,81,86
(1)想一想怎么样比较好
(比较这三种棉花的平均桃数就可能确定! )
(2)为什么比较平均桃数就能确定
(平均数可作为一组数据的数值的代表,要比较某些对象时,往往把这些对象有关数据的平均值进行比较.)
解:设甲、乙、丙三种棉花的平均数分别为:x甲 、x乙、x丙。
x甲=(84+79+81+84+85+82+83+86+87+81)
=83.5(个)
x乙=(85+84+89+79+81+91+79+76+82+84)
=83.0(个)
x丙=(83+85+87+78+80+75+82+83+81+86)
=82.0(个)
由于甲种棉花的平均结桃数高于其他两个品种棉花的结桃数,所以甲品种棉花较好。
思考:通过对上题的解决,你能说出平均数的大小与什么有关吗?
你能说出平均数的作用和特点吗?(学生交流回答,教师点评)
归纳:平均数的大小与一组数据的每个数据都有关系,如果这组数据中的一个数据变大,其平均数将变大;若这组数据中的一个数据变小,平均数将变小。平均数是一组数据的数值大小的集中代表值,它刻画了这组数据整体的平均状态,体现了这组数据的整体性质,对于这组数据的个体性质不能作出什么结论。
活动二:我们来解例2、例3
例2:在一次网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
1号 2号 3号 4号 5号 6号 7号 8号
甲 9.0 9.0 9.2 9.8 8.8 9.2 9.5 9.2
乙 9.4 9.6 9.2 8.0 9.5 9.0 9.2 9.4
你认为哪位选手会胜出?
分析:确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分;二是将评委评分中的一个最高分与一个最低分去掉后的平均数作为最后得分.哪种方案更可取?
解: 按方案一计算甲、乙的最后得分为:
x甲=(8.8+9.0×2+9.2×3+9.5+9.8)
≈9.21(分)
x乙=(8.0+9.0+9.2×2+9.4×2+9.6+9.5)
≈9.16(分)
这时候甲的成绩比乙高
按方案二计算甲、乙的最后得分
y甲=(9.0×2+9.2×3+9.5)
≈9.18(分)
y乙=(9.0+9.2×2+9.4×2+9.5)
≈9.28(分)
这时候乙的成绩比甲高。
结论:将上面的得分与表中的数据相比较,我们发现有5位评委对甲的评分不高于乙,这表明多数人认为乙的成绩比较好。方案二的结果表明乙的成绩比甲的高,与大多数评委的观点相符。因此,方案二评定选手的最后得分比较可取。
例3、个体户张某经营一家餐馆,下面是该餐馆所有工作人员2010年10月份的工资:
张某: 4000元; 会计: 700元; 厨师甲:1000元
厨师乙: 900元; 杂工甲:580元; 杂工乙:560元
服务员甲:620元;服务员乙:600元;服务员丙:580元
(1)计算他们的平均工资,这个平均工资能否反映餐馆员工在这个月收入的一般水平?
(2)不计张某的工资,再求餐馆员工的月平均工资,这个平均工资能代表一般水平吗?
解:(1)设餐馆全体员工的月平均工资为 x1 ,则:
x1=(4000+700+1000+900+580+560+620+600+580)
=1060(元)
(2)设8位员工的月平均工资为 x2 ,则:
x2=(700+1000+900+580+560+620+600+580)
=692.5(元)
结论:1060元不能代表餐馆员工在这个月的月收入的一般水平,因为员工中工资最高的厨师甲的月收入1000元也小于这个平均数。692.5元能代表餐馆员工在这个月的月收入的一般水平。
思考:通过这个问题,你能说出平均数有什么缺点吗?(学生回答,教师点评)
归纳:平均数的缺点:平均数的缺点是容易受个别特殊数据的影响。
想一想:怎样避免这个缺点?(学生讨论,教师点评)
为了消除这个缺点,当出现这种情形时,可以将特殊数据去掉。如某些评奖比赛的计分,通常去掉一个最高分和一个最低分。
三、课堂练习:
试一试:1、小明班上同学的平均身高是1.4米,小强班上同学的平均身高是1.45米,小明一定比小强矮吗?(指名学生回答)
(小明不一定比小强矮,平均数不能对个体特征作出描述。)
2、小王在学校举行的演讲比赛中,10位评委教师所打的分如下:9.6 , 9.5, 9.2 , 9.0,9.4,9.5 ,9.2, 9.3, 8.4, 9.7
你认为怎样计算小王的得分最合理?并求出你认为合理的分数?
学生活动:学生交流,解决,教师点评。(指名学生板演)
练一练:
1、一组数据:40、37、x、64的平均数是53,则x的值是( )
A、67 B、69 C、71 D、72
2、甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲 种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每 斤( )
A、3.88元 B、4.3元 C、8.7元 D、8.8元
3、某次考试A、B、C、D、E五名学生平均分为62分,除 A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、70 D、无法确定
4、某市的7月下旬最高气温统计如下:
气温 35度 34度 33度 32度 28度
天数 2 3 2 2 1
该市7月中旬最高气温的平均数是_____。
5、小明所在班级的男同学的平均体重是45kg,小亮所在班级的男同学的平均体重是42kg,则下列判断正确的是( )
A、小明体重是45kg B、小明比小亮重3kg
C、小明体重不能确定 D、小明与小亮体重相等
四、课堂小结
这节课我们学均数及平均数的计算公式,知道了平均数的计算公式和平均数的作用与特点及平均数的缺点 ,这对我们解决一些与平均数有关的问题将有所帮助。
五、课后作业:课本p135习题20.2 第1、2题
六、板书设计
(
2
0.2
数据的集中趋势与离散程度
――数据的集中趋势(第1课时)
1
、
一般地,如果有n个数据x
1
,x
2
,
…
,x
n
,,那么,
=
(x
1
+x
2
+
…
+x
n
)
2、意义:
3、极端值的影响
:
)
教学反思:
通过这节课的教学,我觉得学生对平均数的计算方法比较容易掌握,所以主要让学生理解过大或过小数据对平均数的影响。
