六年级数学下册课件-7.2.7立体图形的体积 练习 - 苏教版(共17张PPT)
文档属性
| 名称 | 六年级数学下册课件-7.2.7立体图形的体积 练习 - 苏教版(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 10:40:34 | ||
图片预览





文档简介
(共17张PPT)
六年级数学下册
学习目标:
1、进一步熟悉立体图形体积的计算公式,理解这些体积公式的推导过程,会运用公式解决实际问题;
2、能力目标:经历运用公式解决实际问题的过程,培养应用数学知识的意识,发展实践能力;
3、情感目标:在学习中获得成功的体验,对学好数学充满自信心。
长 a
宽 b
高h
棱 长 a
长方体
正方体
圆 锥
圆 柱
高
h
高
h
底面半径 r
底面半径 r
我们学过哪些立体图形
物体所占空间的大小叫做它的体积.
体积的定义?
旧知回顾
长方体的体积 = 长 × 宽 × 高
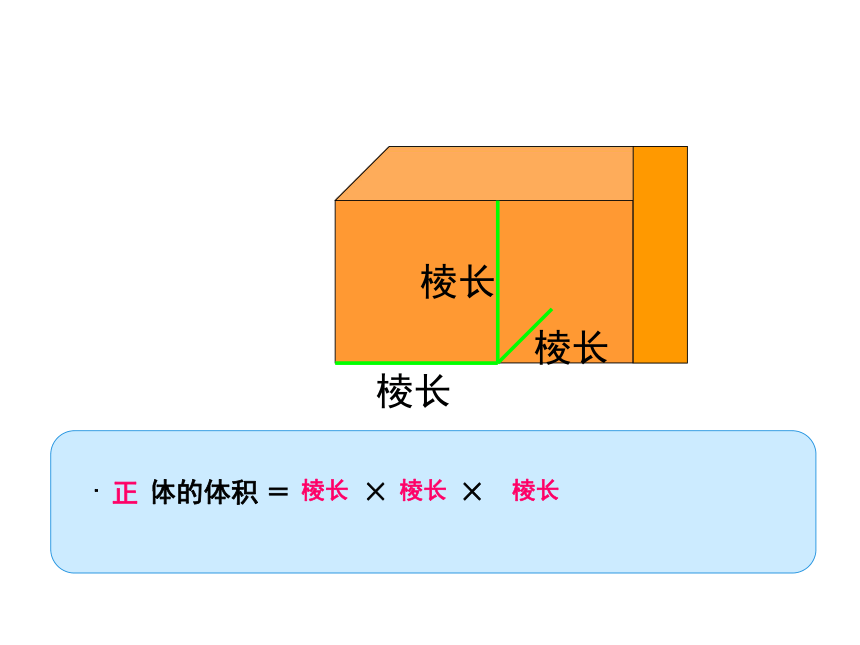
棱长
棱长
棱长
棱长
棱长
棱长
正
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
h
b
a
上
右
前
长方体的体积
=长×宽×高
用字母表示:
V=abh
用字母怎样表示呢
a
a
a
正方体的体积
=棱长×棱长×棱长
=棱长3
用字母表示:
V=a3
用字母怎样表示呢
h
o
o
r
·
圆柱的体积=底面积×高
用字母表示:
V=sh= r2·h
怎样用字母表示呢
圆锥的体积=底面积×高×
h
r
o
·
用字母表示:
V= sh= r2h
怎样用字母表示呢
V=
V=
V=
V=
abh
a
3
sh
1
3
sh
V = sh
长方体、正方体和圆柱的体积计算公式之间有什么联系?
h
a
b
a
a
a
s
h
s
h
动画
知识小结
1、一个长方体沙坑,长5米,宽1.8米,要填40厘米厚的沙,每立方米沙重1.7吨。这个沙坑大约要填多少沙?
40厘米=0.4米
5×1.8×0.4×1.7
=3.6×1.7
=6.12(吨)
答:这个沙坑大约要填6.12吨沙。
巩固提升
2、一个近似于圆锥的沙堆,测得底面直径是4米,高是1.5米。每立方米沙约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)
3.14×(4÷2)2 ×1.5× ×1.7
=6.28×1.7
=10.676(吨)
≈11(吨)
答:这堆沙约重11吨。
巩固提升
3、一根圆柱形木材长20分米,把它截成4个相等的圆柱体. 表面积增加了18平方分米.截后每段圆柱体积是( ).
15立方分米
(18÷6)×(20÷4)
=15(立方分米)
巩固提升
反思提升
将一个底面半径是4分米,高6分米的圆柱体零件熔铸成一个底面直径为4分米的圆锥形零件,求圆锥零件的高是多少分米?
圆柱的体积:3.14×42×6
=50.24×6
=301.44(dm3)
圆锥的高:3.14×(4÷2)2 =12.56(dm 2)
301.44÷1/3÷ 12.56
=904.32÷12.56
=72(dm)
答:圆锥零件的高是72分米。
六年级数学下册
学习目标:
1、进一步熟悉立体图形体积的计算公式,理解这些体积公式的推导过程,会运用公式解决实际问题;
2、能力目标:经历运用公式解决实际问题的过程,培养应用数学知识的意识,发展实践能力;
3、情感目标:在学习中获得成功的体验,对学好数学充满自信心。
长 a
宽 b
高h
棱 长 a
长方体
正方体
圆 锥
圆 柱
高
h
高
h
底面半径 r
底面半径 r
我们学过哪些立体图形
物体所占空间的大小叫做它的体积.
体积的定义?
旧知回顾
长方体的体积 = 长 × 宽 × 高
棱长
棱长
棱长
棱长
棱长
棱长
正
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
h
b
a
上
右
前
长方体的体积
=长×宽×高
用字母表示:
V=abh
用字母怎样表示呢
a
a
a
正方体的体积
=棱长×棱长×棱长
=棱长3
用字母表示:
V=a3
用字母怎样表示呢
h
o
o
r
·
圆柱的体积=底面积×高
用字母表示:
V=sh= r2·h
怎样用字母表示呢
圆锥的体积=底面积×高×
h
r
o
·
用字母表示:
V= sh= r2h
怎样用字母表示呢
V=
V=
V=
V=
abh
a
3
sh
1
3
sh
V = sh
长方体、正方体和圆柱的体积计算公式之间有什么联系?
h
a
b
a
a
a
s
h
s
h
动画
知识小结
1、一个长方体沙坑,长5米,宽1.8米,要填40厘米厚的沙,每立方米沙重1.7吨。这个沙坑大约要填多少沙?
40厘米=0.4米
5×1.8×0.4×1.7
=3.6×1.7
=6.12(吨)
答:这个沙坑大约要填6.12吨沙。
巩固提升
2、一个近似于圆锥的沙堆,测得底面直径是4米,高是1.5米。每立方米沙约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)
3.14×(4÷2)2 ×1.5× ×1.7
=6.28×1.7
=10.676(吨)
≈11(吨)
答:这堆沙约重11吨。
巩固提升
3、一根圆柱形木材长20分米,把它截成4个相等的圆柱体. 表面积增加了18平方分米.截后每段圆柱体积是( ).
15立方分米
(18÷6)×(20÷4)
=15(立方分米)
巩固提升
反思提升
将一个底面半径是4分米,高6分米的圆柱体零件熔铸成一个底面直径为4分米的圆锥形零件,求圆锥零件的高是多少分米?
圆柱的体积:3.14×42×6
=50.24×6
=301.44(dm3)
圆锥的高:3.14×(4÷2)2 =12.56(dm 2)
301.44÷1/3÷ 12.56
=904.32÷12.56
=72(dm)
答:圆锥零件的高是72分米。
