2021-2022学年人教版八年级数学下册17.2勾股定理的逆定理 题型分类训练(Word,带答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.2勾股定理的逆定理 题型分类训练(Word,带答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 296.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览

文档简介
2021-2022学年人教版八年级数学下册《17-2勾股定理的逆定理》题型分类训练(附答案)
一.勾股定理的逆定理
1.下列几组数中,不能作为直角三角形三边长的是( )
A.5,12,13 B.9,40,41
C.0.5,1.2,1.3 D.2,3,4
2.下列条件中,不能判定△ABC是直角三角形的是( )
A.∠A=∠B+∠C B.a:b:c=5:12:13
C.a2=(b+c)(b﹣c) D.∠A:∠B:∠C=3:4:5
3.适合下列条件的△ABC中,是直角三角形的个数为( )
①a:b:c=3:4:5
②∠A=32°,∠B=58°
③a=5,b=12,c=13
④a=7,b=24,c=25
⑤a=2,b=2,c=4
⑥∠A:∠B:∠C=1:2:3
A.2个 B.3个 C.4个 D.5个
4.已知a,b,c分别为△ABC的三边长,则符合下列条件的△ABC中,直角三角形有( )
(1)a=,b=,c=;(2)a2=(b+c)(b﹣c);(3)∠A:∠B:∠C=3:4:5;(4)a=7,b=24,c=25; (5)a=2,b=2,c=4.
A.2个 B.3个 C.4个 D.5个
5.△ABC的三边为a、b、c,且(a+b)(a﹣b)=c2,则( )
A.△ABC是锐角三角形 B.c边的对角是直角
C.△ABC是钝角三角形 D.a边的对角是直角
6.三角形的三边长有下列关系:(a﹣b)2=c2﹣2ab,则这个三角形是( )
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
7.已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )
A.等边三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
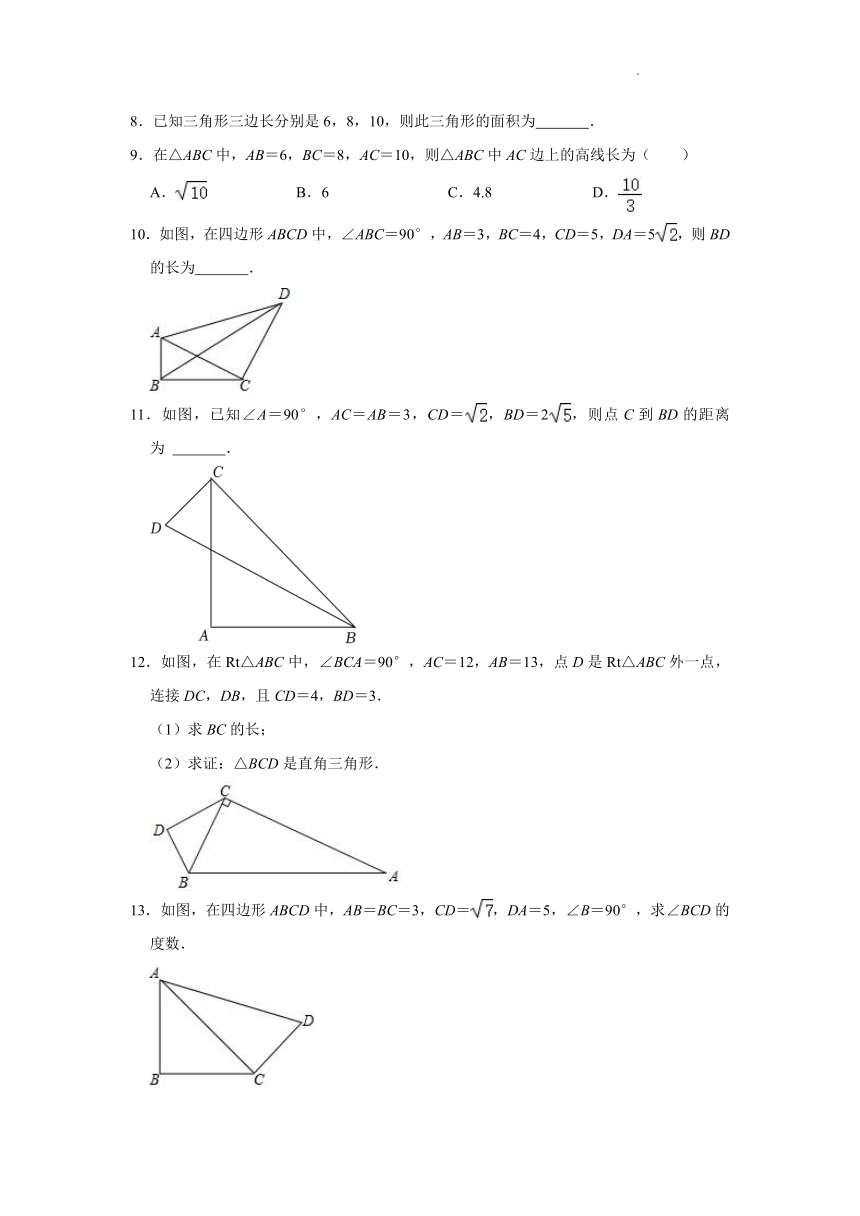
8.已知三角形三边长分别是6,8,10,则此三角形的面积为 .
9.在△ABC中,AB=6,BC=8,AC=10,则△ABC中AC边上的高线长为( )
A. B.6 C.4.8 D.
10.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5,则BD的长为 .
11.如图,已知∠A=90°,AC=AB=3,CD=,BD=2,则点C到BD的距离为 .
12.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.
(1)求BC的长;
(2)求证:△BCD是直角三角形.
13.如图,在四边形ABCD中,AB=BC=3,CD=,DA=5,∠B=90°,求∠BCD的度数.
14.已知:如图,△ABC中,CD⊥AB,AB=2,BC=2,AC=4.
(1)求证:△ABC是直角三角形;
(2)求CD的长.
15.如图,点C是线段BD上的一点,∠B=∠D=90°,AB=3,BC=2,CD=6,DE=4,AE=,求证:∠ACE=90°.
二.勾股数
16.在下列各组数中,是勾股数的是( )
A.1、2、3 B.2、3、4 C.3、4、5 D.4、5、6
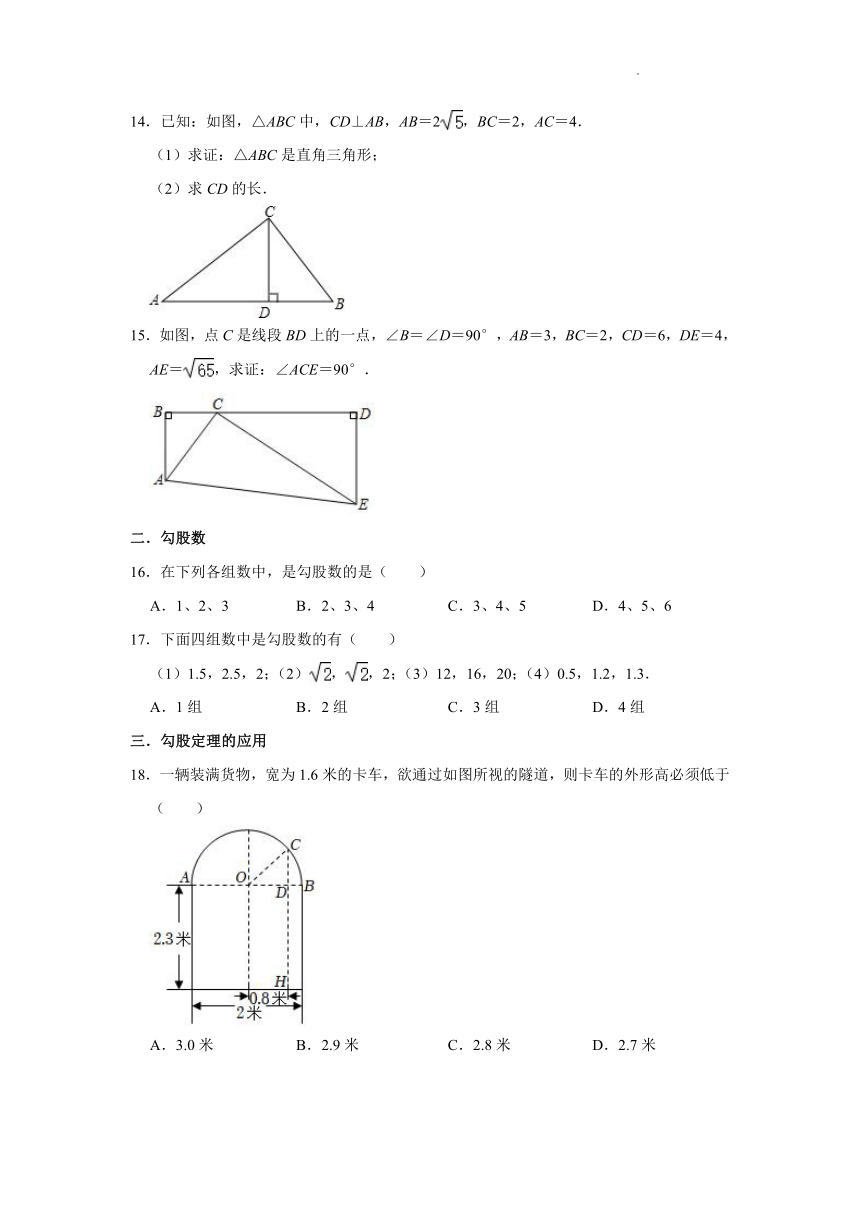
17.下面四组数中是勾股数的有( )
(1)1.5,2.5,2;(2),,2;(3)12,16,20;(4)0.5,1.2,1.3.
A.1组 B.2组 C.3组 D.4组
三.勾股定理的应用
18.一辆装满货物,宽为1.6米的卡车,欲通过如图所视的隧道,则卡车的外形高必须低于( )
A.3.0米 B.2.9米 C.2.8米 D.2.7米
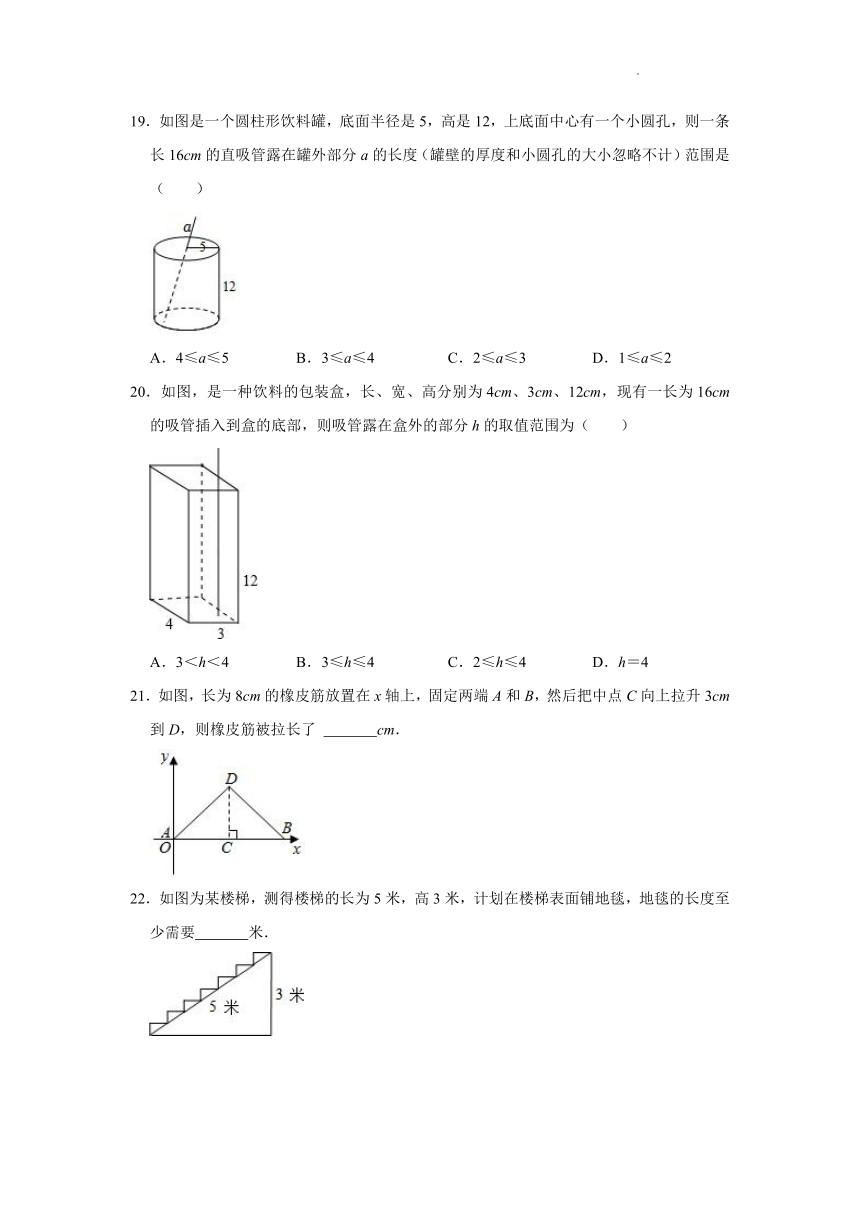
19.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条长16cm的直吸管露在罐外部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.4≤a≤5 B.3≤a≤4 C.2≤a≤3 D.1≤a≤2
20.如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为( )
A.3<h<4 B.3≤h≤4 C.2≤h≤4 D.h=4
21.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm到D,则橡皮筋被拉长了 cm.
22.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米.
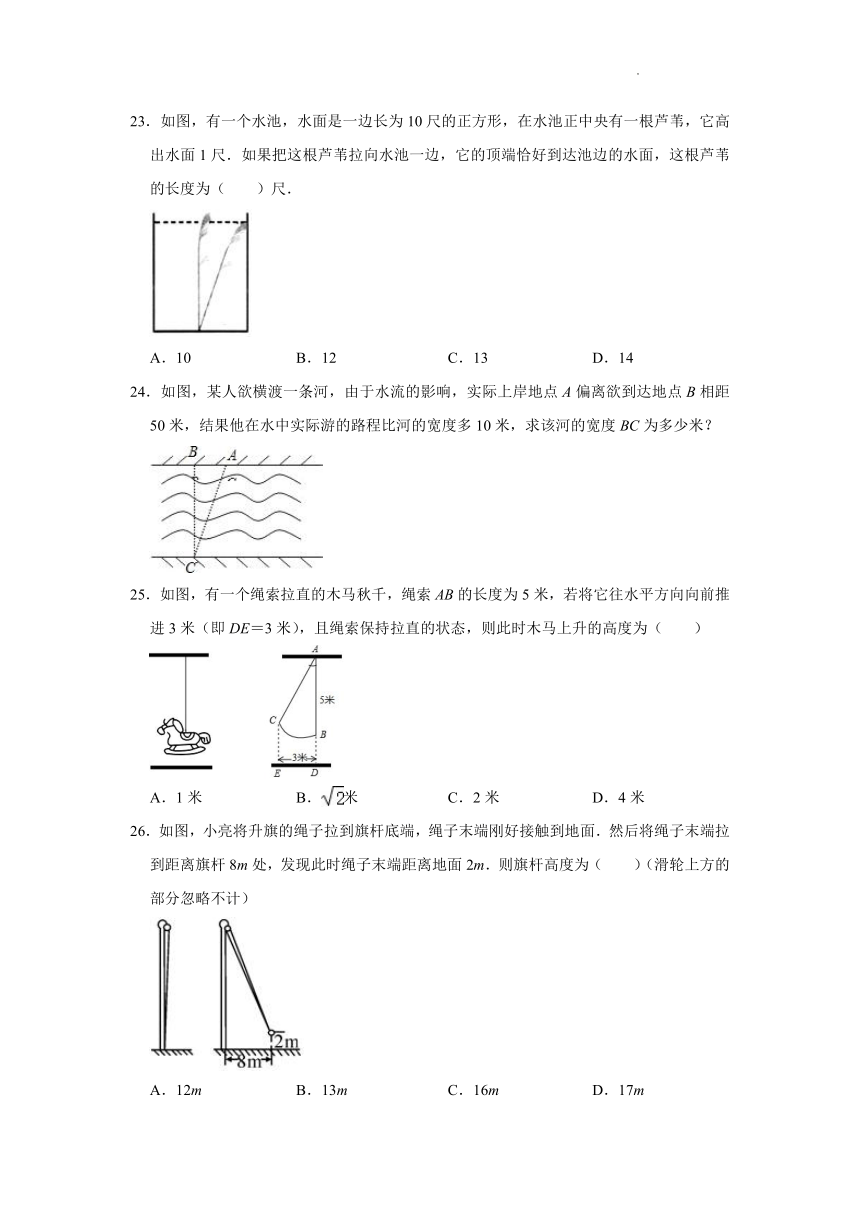
23.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.10 B.12 C.13 D.14
24.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点A偏离欲到达地点B相距50米,结果他在水中实际游的路程比河的宽度多10米,求该河的宽度BC为多少米?
25.如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( )
A.1米 B.米 C.2米 D.4米
26.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面.然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m.则旗杆高度为( )(滑轮上方的部分忽略不计)
A.12m B.13m C.16m D.17m
27.如图所示,在一棵树的10米高的B处有两只猴子,一只猴子爬下树走到离树20米的A处.另一只猴子爬到树顶D处后顺绳子滑到A处,如果两只猴子所经过的距离相等,则这棵树高 米.
28.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
29.如图,高速公路上有A、B两点相距25km,C、D为两村庄,已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则AE的长是( )km.
A.5 B.10 C.15 D.25
30.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.2.2米 B.2.3米 C.2.4米 D.2.5米
31.如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
32.如图,淇淇在离水面高度为5m的岸边C处,用绳子拉船靠岸,开始时绳子BC的长为13m.
(1)开始时,船距岸A的距离是 m;
(2)若淇淇收绳5m后,船到达D处,则船向岸A移动 m.
33.如图,在一条绷紧的绳索一端系着一艘小船.河岸上一男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,且绳长始终保持不变.回答下列问题:
(1)根据题意可知:AC BC+CE(填“>”、“<”、“=”).
(2)若CF=5米,AF=12米,AB=9米,求小男孩需向右移动的距离.(结果保留根号)
34.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30米C处,过了2秒后,小汽车行驶到B处,测得小汽车与车速检测仪间距离为50米,
(1)求BC的长;
(2)这辆小汽车超速了吗?
35.在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?请通过计算进行说明.
36.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A,B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)求∠ACB的度数;
(2)海港C受台风影响吗?为什么?
(3)若台风的速度为20千米/小时,当台风运动到点E处时,海港C刚好受到影响,当台风运动到点F时,海港C刚好不受影响,即CE=CF=250km,则台风影响该海港持续的时间有多长?
37.如图,现对校园中的一块空地进行美化施工,已知AB=3米,BC=4米,∠ABC=90°,AD=12米,CD=13米,学校欲在此空地上铺草坪,已知草坪每平方米80元,试问用该草坪铺满这块空地共需花费多少元?
38.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米80元,试问铺满这块空地共需花费多少元?
39.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,在A处有一所中学,AP=120米,此时有一辆消防车在公路MN上沿PN方向以每秒5米的速度行驶,假设消防车行驶时周围100米以内有噪音影响.
(1)学校是否会受到影响?请说明理由.
(2)如果受到影响,则影响时间是多长?
40.如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
参考答案
一.勾股定理的逆定理
1.解:A、52+122=132,能作为直角三角形的三边长,故本选项不符合题意.
B、92+402=412,能作为直角三角形的三边长,故本选项不符合题意.
C、0.52+1.22=1.32,能作为直角三角形的三边长,故本选项不符合题意.
D、22+32≠42,不能作为直角三角形的三边长,故本选项符合题意.
故选:D.
2.解:A、∵∠A=∠B+∠C,∠A+∠B+∠C=180°,
∴∠A=90°,
∴△ABC为直角三角形,故此选项不合题意;
B、∵52+122=132,
∴能构成直角三角形,故此选项不符合题意;
C、∵a2=(b+c)(b﹣c),即a2=b2﹣c2,
∴b2=a2+c2,
∴能构成直角三角形,故此选项不符合题意;
D、设∠A=3x°,∠B=4x°,∠C=5x°,
3x+4x+5x=180,
解得:x=15,
则5x°=75°,
△ABC不是直角三角形,故此选项符合题意.
故选:D.
3.解:①∵a:b:c=3:4:5,
∴设a=3x,则b=4x,c=5x,
∴(3x)2+(4x)2=25x2,c2=(5x)2,
∴a2+b2=c2,
∴△ABC为直角三角形;
②∵∠A=32°,∠B=58°,
∴∠C=180°﹣32°﹣58°=90°,
∴△ABC为直角三角形;
③∵a2+b2=52+122=169,c2=132=169,
∴a2+b2=c2,
∴△ABC为直角三角形;
④∵a2+b2=72+242=625,c2=252=625,
∴a2+b2=c2,
∴△ABC为直角三角形;
⑤∵a2+b2=22+22=8,c2=42=16,
∴a2+b2≠c2,
∴△ABC不是直角三角形;
⑥设∠A=x,∠B=2x,∠C=3x,
∴x+2x+3x=180°,
解得x=30°,
∴∠C=90°,
∴△ABC为直角三角形.
故选:D.
4.解:(1)由a=,b=,c=可得,a2≠b2+c2,故△ABC不是直角三角形;
(2)由a2=(b+c)(b﹣c)可得,a2+c2=b2,故△ABC是直角三角形;
(3)由∠A:∠B:∠C=3:4:5可得,∠C=180°×=75°<90°,故△ABC不是直角三角形;
(4)由a=7,b=24,c=25可得,c2=a2+b2,故△ABC为直角三角形;
(5)由a=2,b=2,c=4可得,a+b=c,故不能构成三角形.
故选:A.
5.解:∵(a+b)(a﹣b)=c2,
∴a2=b2+c2,
∴△ABC是直角三角形,a为斜边,
∴a边的对角是直角.
故选:D.
6.解:∵(a﹣b)2=c2﹣2ab,
∴a2﹣2ab+b2=c2﹣2ab,
∴a2+b2=c2,
∴这个三角形是直角三角形.
故选:C.
7.解:∵(a﹣b)(a2+b2﹣c2)=0,
∴a﹣b=0,或a2+b2﹣c2=0,
即a=b或a2+b2=c2,
∴△ABC的形状为等腰三角形或直角三角形.
故选:D.
8.解:∵62+82=102,
∴此三角形为直角三角形,
∴此三角形的面积为:×6×8=24.
故答案为:24.
9.解:设AC边上的高线为h,
∵△ABC中,AB=6,BC=8,AC=10,
∴62+82=102,即AB2+BC2=AC2,
∴△ABC是直角三角形,
∴S△ABC=AB BC=
即×6×8=
h=4.8.
故选:C.
10.解:作DM⊥BC,交BC延长线于M,如图所示:
则∠M=90°,
∴∠DCM+∠CDM=90°,
∵∠ABC=90°,AB=3,BC=4,
∴AC2=AB2+BC2=25,
∴AC=5,
∵AD=5,CD=5,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠CDM,
∵∠ABC=∠M=90°,
在△ABC和△CMD中
∴△ABC≌△CMD,
∴CM=AB=3,DM=BC=4,
∴BM=BC+CM=7,
∴BD===,
故答案为:.
11.解:∵∠A=90°,AC=AB=3,
∴BC===3,
∵CD=,BD=2,
()2+(3)2=(2)2,
∴△BCD是直角三角形,
∴点C到BD的距离为×3÷2×2÷2=.
故答案为:.
12.(1)解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC===5;
(2)证明:∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=42+32=52=BC2,
∴△BCD是直角三角形.
13.解:∵在Rt△ABC中,AB=BC=3,∠B=90°,
∴由勾股定理得:AC2=AB2+BC2=32+32=18,
∵CD=,DA=5,
∴CD2+AC2=DA2,
∴∠ACD=90°,
∵在Rt△ABC中,AB=BC,
∴∠BAC=∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=45°+90°=135°.
14.证明:(1)∵AB=2,BC=2,AC=4.
∵AC2+BC2=20=AB2,
∴△ABC是直角三角形;
(2)∵△ABC是直角三角形,
∴CD=.
15.证明:在Rt△ABC中,∠B=90°,AB=3,BC=2,
∴AC===.
在Rt△EDC中,∠D=90°,CD=6,DE=4,
∴CE===2,
∵AC2=13,CE2=52,AE2=65,
∴AE2=AC2+CE2,
∴△ACE是直角三角形,AE是斜边,
∴∠ACE=90°.
二.勾股数
16.解:A、12+22=5≠32,不是勾股数,故本选项不符合题意.
B、22+32=13≠42,不是勾股数,故本选项不符合题意.
C、32+42=52,是勾股数,故本选项符合题意.
D、42+52=41≠62,不是勾股数,故本选项不符合题意.
故选:C.
17.解:(1)1.52+22=2.52,但不是正整数,故错误;
(2)()2+()2=22,能构成直角三角形,但不是整数,故错误;
(3)122+162=202,三边是整数,同时能构成直角三角形,故正确;
(4)0.52+1.22=1.32,但不是正整数,故错误.
故选:A.
三.勾股定理的应用
18.解:∵车宽1.6米,
∴欲通过如图的隧道,只要比较距隧道中线0.8米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===0.6(米),
∴CH=CD+DH=0.6+2.3=2.9(米),
∴卡车的外形高必须低于2.9米.
故选:B.
19.解:如图,
当吸管底部在地面圆心时吸管在罐内部分b最短,
此时b就是圆柱形的高,
即b=12cm;
∴a=16﹣12=4(cm),
当吸管底部在饮料罐的壁底时吸管在罐内部分b最长,
b==13(cm),
∴此时a=3,
所以3≤a≤4.
故选:B.
20.解:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16﹣12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线直径为5cm,高为12cm,
由勾股定理可得杯里面管长为=13cm,则露在杯口外的长度最长为16﹣13=3cm;
则可得露在杯口外的长度在3cm和4cm范围变化.
故选:B.
21.解:Rt△ACD中,AC=AB=4cm,CD=3cm;
根据勾股定理,得:AD==5cm;
∴AD+BD﹣AB=2AD﹣AB=10﹣8=2cm;
故橡皮筋被拉长了2cm.
22.解:由勾股定理得:
楼梯的水平宽度==4,
∵地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故答案为7.
23.解:设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+()2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺),
答:芦苇长13尺.
故选:C.
24.解:根据题意可知AB=50米,AC=BC+10米,
设BC=x,由勾股定理得AC2=AB2+BC2,
即(x+10)2=502+x2,解得x=120.
答:该河的宽度BC为120米.
25.解:过点C作CF⊥AB于点F,
根据题意得:AB=AC=5,CF=DE=3,
由勾股定理可得AF2+CF2=AC2,
∴AF=,
∴BF=AB﹣AF=5﹣4=1,
∴此时木马上升的高度为1米,
故选:A.
26.解:设旗杆高度为x,则AC=AD=x,AB=(x﹣2)m,BC=8m,
在Rt△ABC中,AB2+BC2=AC2,即(x﹣2)2+82=x2,
解得:x=17,
即旗杆的高度为17米.
故选:D.
27.解:由题意得,CD=x+10,AC=20米,
在Rt△ADC中,AD==,
∵两只猴子所经过的距离相等,
∴BC+CA=BD+DA,即10+20=x+,
解得:x=5,即树高10+5=15米.
故答案为:15.
28.解:Rt△ABC中,∠B=90°,
设BC=a(m),AC=b(m),AD=x(m)
则10+a=x+b=15(m).
∴a=5(m),b=15﹣x(m)
又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2,
∴(10+x)2+52=(15﹣x)2,
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米.
29.解:设AE=x,则BE=25﹣x,
由勾股定理得:
在Rt△ADE中,
DE2=AD2+AE2=102+x2,
在Rt△BCE中,
CE2=BC2+BE2=152+(25﹣x)2,
由题意可知:DE=CE,
所以:102+x2=152+(25﹣x)2,
解得:x=15km.
所以,E应建在距A点15km处.
故选:C.
30.解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.
在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B2,
∴BD2+22=6.25,
∴BD2=2.25,
∵BD>0,
∴BD=1.5米,
∴CD=BC+BD=0.7+1.5=2.2米.
故选:A.
31.解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,即BC=CA,设AC为x,则OC=45﹣x,
由勾股定理可知OB2+OC2=BC2,
又∵OA=45,OB=15,
把它代入关系式152+(45﹣x)2=x2,
解方程得出x=25(cm).
答:如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是25cm.
32.解:(1)在Rt△ABC中,∠CAB=90°,BC=13m,AC=5m,
∴(m),
故答案为:12;
(2)∵淇淇收绳5m后,船到达D处,
∴CD=8(m),
∴AD=(m),
∴BD=AB﹣AD=(12﹣)m.
故答案为:(12﹣).
33.解:(1)∵AC的长度是男孩未拽之前的绳子长,(BC+CE)的长度是男孩拽之后的绳子长,绳长始终保持不变,
∴AC=BC+CE,
故答案为:=;
(2)连接AB,如图所示:
则点A、B、F三点共线,
在Rt△CFA中,由勾股定理得:AC===13(米),
∵BF=AF﹣AB=12﹣9=3(米),
在Rt△CFB中,由勾股定理得:BC===(米),
由(1)得:AC=BC+CE,
∴CE=AC﹣BC=(13﹣)(米),
∴小男孩需向右移动的距离为(13﹣)米.
34.解:(1)在直角△ABC中,已知AC=30米,AB=50米,
且AB为斜边,则BC==40米.
答:小汽车在2秒内行驶的距离BC为40米;
(2)小汽车在2秒内行驶了40米,所以平均速度为20米/秒,
20米/秒=72千米/时,
因为72>70,
所以这辆小汽车超速了.
答:这辆小汽车的平均速度大于70千米/时,故这辆小汽车超速了.
35.解:公路AB需要暂时封锁.
理由如下:如图,过C作CD⊥AB于D.
因为BC=400米,AC=300米,∠ACB=90°,
所以根据勾股定理有AB=500米.
因为S△ABC=AB CD=BC AC
所以CD===240米.
由于240米<250米,故有危险,
因此AB段公路需要暂时封锁.
36.解:(1)∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)海港C受台风影响,
理由:过点C作CD⊥AB,
∵△ABC是直角三角形,
∴AC×BC=CD×AB,
∴300×400=500×CD,
∴CD=240(km),
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受台风影响;
(3)当EC=250km,FC=250km时,正好影响C港口,
∵ED==70(km),
∴EF=140km,
∵台风的速度为20千米/小时,
∴140÷20=7(小时).
答:台风影响该海港持续的时间为7小时.
37.解:连接AC,在Rt△ABC中,AB=3米,BC=4米,
∵AC2=AB2+BC2=32+42=25,
∴AC=5,
∵AC2+AD2=52+122=169,CD2=132=169,
∴AC2+AD2=CD2,
∴∠DAC=90°,
该区域面积=S△ACD﹣S△ABC=30﹣6=24(平方米),
铺满这块空地共需花费=24×80=1920(元).
答:用该草坪铺满这块空地共需花费1920元.
38.解:(1)如图,连接AC,
在Rt△ABC中,∵AB=3m,BC=4m,∠B=90°,AB2+CB2=AC2
∴AC=5cm,
在△ACD中,AC=5cmCD=12m,DA=13m,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°;
(2)∵S△ABC=×3×4=6,S△ACD=×5×12=30,
∴S四边形ABCD=6+30=36,
费用=36×80=2880(元).
答:铺满这块空地共需花费2880元.
39.解:(1)学校受到噪音影响.理由如下:
作AB⊥MN于B,如图1,
∵PA=120m,∠QPN=30°,
∴AB=PA=60m,
而60m<100m,
∴消防车在公路MN上沿PN方向行驶时,学校受到噪音影响;
(2)以点A为圆心,100m为半径作⊙A交MN于C、D,如图,
∵AB⊥CD,
∴CB=BD,
在Rt△ABC中,AC=100m,AB=60m,
CB==80m,
∴CD=2BC=160m,
∵消防车的速度5m/s,
∴消防车在线段CD上行驶所需要的时间=160÷5=32(秒),
∴学校受影响的时间为32秒.
40.解:∵甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行,
∴AO⊥BO,
∵甲以20海里/时的速度向南偏东45°方向航行,
∴OB=20×2=40(海里),
∵AB=50海里,
在Rt△AOB中,,
∴乙轮船平均每小时航行30÷2=15海里.
一.勾股定理的逆定理
1.下列几组数中,不能作为直角三角形三边长的是( )
A.5,12,13 B.9,40,41
C.0.5,1.2,1.3 D.2,3,4
2.下列条件中,不能判定△ABC是直角三角形的是( )
A.∠A=∠B+∠C B.a:b:c=5:12:13
C.a2=(b+c)(b﹣c) D.∠A:∠B:∠C=3:4:5
3.适合下列条件的△ABC中,是直角三角形的个数为( )
①a:b:c=3:4:5
②∠A=32°,∠B=58°
③a=5,b=12,c=13
④a=7,b=24,c=25
⑤a=2,b=2,c=4
⑥∠A:∠B:∠C=1:2:3
A.2个 B.3个 C.4个 D.5个
4.已知a,b,c分别为△ABC的三边长,则符合下列条件的△ABC中,直角三角形有( )
(1)a=,b=,c=;(2)a2=(b+c)(b﹣c);(3)∠A:∠B:∠C=3:4:5;(4)a=7,b=24,c=25; (5)a=2,b=2,c=4.
A.2个 B.3个 C.4个 D.5个
5.△ABC的三边为a、b、c,且(a+b)(a﹣b)=c2,则( )
A.△ABC是锐角三角形 B.c边的对角是直角
C.△ABC是钝角三角形 D.a边的对角是直角
6.三角形的三边长有下列关系:(a﹣b)2=c2﹣2ab,则这个三角形是( )
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
7.已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )
A.等边三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
8.已知三角形三边长分别是6,8,10,则此三角形的面积为 .
9.在△ABC中,AB=6,BC=8,AC=10,则△ABC中AC边上的高线长为( )
A. B.6 C.4.8 D.
10.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5,则BD的长为 .
11.如图,已知∠A=90°,AC=AB=3,CD=,BD=2,则点C到BD的距离为 .
12.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.
(1)求BC的长;
(2)求证:△BCD是直角三角形.
13.如图,在四边形ABCD中,AB=BC=3,CD=,DA=5,∠B=90°,求∠BCD的度数.
14.已知:如图,△ABC中,CD⊥AB,AB=2,BC=2,AC=4.
(1)求证:△ABC是直角三角形;
(2)求CD的长.
15.如图,点C是线段BD上的一点,∠B=∠D=90°,AB=3,BC=2,CD=6,DE=4,AE=,求证:∠ACE=90°.
二.勾股数
16.在下列各组数中,是勾股数的是( )
A.1、2、3 B.2、3、4 C.3、4、5 D.4、5、6
17.下面四组数中是勾股数的有( )
(1)1.5,2.5,2;(2),,2;(3)12,16,20;(4)0.5,1.2,1.3.
A.1组 B.2组 C.3组 D.4组
三.勾股定理的应用
18.一辆装满货物,宽为1.6米的卡车,欲通过如图所视的隧道,则卡车的外形高必须低于( )
A.3.0米 B.2.9米 C.2.8米 D.2.7米
19.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条长16cm的直吸管露在罐外部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.4≤a≤5 B.3≤a≤4 C.2≤a≤3 D.1≤a≤2
20.如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为( )
A.3<h<4 B.3≤h≤4 C.2≤h≤4 D.h=4
21.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm到D,则橡皮筋被拉长了 cm.
22.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米.
23.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.10 B.12 C.13 D.14
24.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点A偏离欲到达地点B相距50米,结果他在水中实际游的路程比河的宽度多10米,求该河的宽度BC为多少米?
25.如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( )
A.1米 B.米 C.2米 D.4米
26.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面.然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m.则旗杆高度为( )(滑轮上方的部分忽略不计)
A.12m B.13m C.16m D.17m
27.如图所示,在一棵树的10米高的B处有两只猴子,一只猴子爬下树走到离树20米的A处.另一只猴子爬到树顶D处后顺绳子滑到A处,如果两只猴子所经过的距离相等,则这棵树高 米.
28.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
29.如图,高速公路上有A、B两点相距25km,C、D为两村庄,已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则AE的长是( )km.
A.5 B.10 C.15 D.25
30.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.2.2米 B.2.3米 C.2.4米 D.2.5米
31.如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
32.如图,淇淇在离水面高度为5m的岸边C处,用绳子拉船靠岸,开始时绳子BC的长为13m.
(1)开始时,船距岸A的距离是 m;
(2)若淇淇收绳5m后,船到达D处,则船向岸A移动 m.
33.如图,在一条绷紧的绳索一端系着一艘小船.河岸上一男孩拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,且绳长始终保持不变.回答下列问题:
(1)根据题意可知:AC BC+CE(填“>”、“<”、“=”).
(2)若CF=5米,AF=12米,AB=9米,求小男孩需向右移动的距离.(结果保留根号)
34.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30米C处,过了2秒后,小汽车行驶到B处,测得小汽车与车速检测仪间距离为50米,
(1)求BC的长;
(2)这辆小汽车超速了吗?
35.在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?请通过计算进行说明.
36.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A,B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)求∠ACB的度数;
(2)海港C受台风影响吗?为什么?
(3)若台风的速度为20千米/小时,当台风运动到点E处时,海港C刚好受到影响,当台风运动到点F时,海港C刚好不受影响,即CE=CF=250km,则台风影响该海港持续的时间有多长?
37.如图,现对校园中的一块空地进行美化施工,已知AB=3米,BC=4米,∠ABC=90°,AD=12米,CD=13米,学校欲在此空地上铺草坪,已知草坪每平方米80元,试问用该草坪铺满这块空地共需花费多少元?
38.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米80元,试问铺满这块空地共需花费多少元?
39.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,在A处有一所中学,AP=120米,此时有一辆消防车在公路MN上沿PN方向以每秒5米的速度行驶,假设消防车行驶时周围100米以内有噪音影响.
(1)学校是否会受到影响?请说明理由.
(2)如果受到影响,则影响时间是多长?
40.如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
参考答案
一.勾股定理的逆定理
1.解:A、52+122=132,能作为直角三角形的三边长,故本选项不符合题意.
B、92+402=412,能作为直角三角形的三边长,故本选项不符合题意.
C、0.52+1.22=1.32,能作为直角三角形的三边长,故本选项不符合题意.
D、22+32≠42,不能作为直角三角形的三边长,故本选项符合题意.
故选:D.
2.解:A、∵∠A=∠B+∠C,∠A+∠B+∠C=180°,
∴∠A=90°,
∴△ABC为直角三角形,故此选项不合题意;
B、∵52+122=132,
∴能构成直角三角形,故此选项不符合题意;
C、∵a2=(b+c)(b﹣c),即a2=b2﹣c2,
∴b2=a2+c2,
∴能构成直角三角形,故此选项不符合题意;
D、设∠A=3x°,∠B=4x°,∠C=5x°,
3x+4x+5x=180,
解得:x=15,
则5x°=75°,
△ABC不是直角三角形,故此选项符合题意.
故选:D.
3.解:①∵a:b:c=3:4:5,
∴设a=3x,则b=4x,c=5x,
∴(3x)2+(4x)2=25x2,c2=(5x)2,
∴a2+b2=c2,
∴△ABC为直角三角形;
②∵∠A=32°,∠B=58°,
∴∠C=180°﹣32°﹣58°=90°,
∴△ABC为直角三角形;
③∵a2+b2=52+122=169,c2=132=169,
∴a2+b2=c2,
∴△ABC为直角三角形;
④∵a2+b2=72+242=625,c2=252=625,
∴a2+b2=c2,
∴△ABC为直角三角形;
⑤∵a2+b2=22+22=8,c2=42=16,
∴a2+b2≠c2,
∴△ABC不是直角三角形;
⑥设∠A=x,∠B=2x,∠C=3x,
∴x+2x+3x=180°,
解得x=30°,
∴∠C=90°,
∴△ABC为直角三角形.
故选:D.
4.解:(1)由a=,b=,c=可得,a2≠b2+c2,故△ABC不是直角三角形;
(2)由a2=(b+c)(b﹣c)可得,a2+c2=b2,故△ABC是直角三角形;
(3)由∠A:∠B:∠C=3:4:5可得,∠C=180°×=75°<90°,故△ABC不是直角三角形;
(4)由a=7,b=24,c=25可得,c2=a2+b2,故△ABC为直角三角形;
(5)由a=2,b=2,c=4可得,a+b=c,故不能构成三角形.
故选:A.
5.解:∵(a+b)(a﹣b)=c2,
∴a2=b2+c2,
∴△ABC是直角三角形,a为斜边,
∴a边的对角是直角.
故选:D.
6.解:∵(a﹣b)2=c2﹣2ab,
∴a2﹣2ab+b2=c2﹣2ab,
∴a2+b2=c2,
∴这个三角形是直角三角形.
故选:C.
7.解:∵(a﹣b)(a2+b2﹣c2)=0,
∴a﹣b=0,或a2+b2﹣c2=0,
即a=b或a2+b2=c2,
∴△ABC的形状为等腰三角形或直角三角形.
故选:D.
8.解:∵62+82=102,
∴此三角形为直角三角形,
∴此三角形的面积为:×6×8=24.
故答案为:24.
9.解:设AC边上的高线为h,
∵△ABC中,AB=6,BC=8,AC=10,
∴62+82=102,即AB2+BC2=AC2,
∴△ABC是直角三角形,
∴S△ABC=AB BC=
即×6×8=
h=4.8.
故选:C.
10.解:作DM⊥BC,交BC延长线于M,如图所示:
则∠M=90°,
∴∠DCM+∠CDM=90°,
∵∠ABC=90°,AB=3,BC=4,
∴AC2=AB2+BC2=25,
∴AC=5,
∵AD=5,CD=5,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠CDM,
∵∠ABC=∠M=90°,
在△ABC和△CMD中
∴△ABC≌△CMD,
∴CM=AB=3,DM=BC=4,
∴BM=BC+CM=7,
∴BD===,
故答案为:.
11.解:∵∠A=90°,AC=AB=3,
∴BC===3,
∵CD=,BD=2,
()2+(3)2=(2)2,
∴△BCD是直角三角形,
∴点C到BD的距离为×3÷2×2÷2=.
故答案为:.
12.(1)解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC===5;
(2)证明:∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=42+32=52=BC2,
∴△BCD是直角三角形.
13.解:∵在Rt△ABC中,AB=BC=3,∠B=90°,
∴由勾股定理得:AC2=AB2+BC2=32+32=18,
∵CD=,DA=5,
∴CD2+AC2=DA2,
∴∠ACD=90°,
∵在Rt△ABC中,AB=BC,
∴∠BAC=∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=45°+90°=135°.
14.证明:(1)∵AB=2,BC=2,AC=4.
∵AC2+BC2=20=AB2,
∴△ABC是直角三角形;
(2)∵△ABC是直角三角形,
∴CD=.
15.证明:在Rt△ABC中,∠B=90°,AB=3,BC=2,
∴AC===.
在Rt△EDC中,∠D=90°,CD=6,DE=4,
∴CE===2,
∵AC2=13,CE2=52,AE2=65,
∴AE2=AC2+CE2,
∴△ACE是直角三角形,AE是斜边,
∴∠ACE=90°.
二.勾股数
16.解:A、12+22=5≠32,不是勾股数,故本选项不符合题意.
B、22+32=13≠42,不是勾股数,故本选项不符合题意.
C、32+42=52,是勾股数,故本选项符合题意.
D、42+52=41≠62,不是勾股数,故本选项不符合题意.
故选:C.
17.解:(1)1.52+22=2.52,但不是正整数,故错误;
(2)()2+()2=22,能构成直角三角形,但不是整数,故错误;
(3)122+162=202,三边是整数,同时能构成直角三角形,故正确;
(4)0.52+1.22=1.32,但不是正整数,故错误.
故选:A.
三.勾股定理的应用
18.解:∵车宽1.6米,
∴欲通过如图的隧道,只要比较距隧道中线0.8米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===0.6(米),
∴CH=CD+DH=0.6+2.3=2.9(米),
∴卡车的外形高必须低于2.9米.
故选:B.
19.解:如图,
当吸管底部在地面圆心时吸管在罐内部分b最短,
此时b就是圆柱形的高,
即b=12cm;
∴a=16﹣12=4(cm),
当吸管底部在饮料罐的壁底时吸管在罐内部分b最长,
b==13(cm),
∴此时a=3,
所以3≤a≤4.
故选:B.
20.解:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16﹣12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线直径为5cm,高为12cm,
由勾股定理可得杯里面管长为=13cm,则露在杯口外的长度最长为16﹣13=3cm;
则可得露在杯口外的长度在3cm和4cm范围变化.
故选:B.
21.解:Rt△ACD中,AC=AB=4cm,CD=3cm;
根据勾股定理,得:AD==5cm;
∴AD+BD﹣AB=2AD﹣AB=10﹣8=2cm;
故橡皮筋被拉长了2cm.
22.解:由勾股定理得:
楼梯的水平宽度==4,
∵地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故答案为7.
23.解:设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+()2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺),
答:芦苇长13尺.
故选:C.
24.解:根据题意可知AB=50米,AC=BC+10米,
设BC=x,由勾股定理得AC2=AB2+BC2,
即(x+10)2=502+x2,解得x=120.
答:该河的宽度BC为120米.
25.解:过点C作CF⊥AB于点F,
根据题意得:AB=AC=5,CF=DE=3,
由勾股定理可得AF2+CF2=AC2,
∴AF=,
∴BF=AB﹣AF=5﹣4=1,
∴此时木马上升的高度为1米,
故选:A.
26.解:设旗杆高度为x,则AC=AD=x,AB=(x﹣2)m,BC=8m,
在Rt△ABC中,AB2+BC2=AC2,即(x﹣2)2+82=x2,
解得:x=17,
即旗杆的高度为17米.
故选:D.
27.解:由题意得,CD=x+10,AC=20米,
在Rt△ADC中,AD==,
∵两只猴子所经过的距离相等,
∴BC+CA=BD+DA,即10+20=x+,
解得:x=5,即树高10+5=15米.
故答案为:15.
28.解:Rt△ABC中,∠B=90°,
设BC=a(m),AC=b(m),AD=x(m)
则10+a=x+b=15(m).
∴a=5(m),b=15﹣x(m)
又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2,
∴(10+x)2+52=(15﹣x)2,
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米.
29.解:设AE=x,则BE=25﹣x,
由勾股定理得:
在Rt△ADE中,
DE2=AD2+AE2=102+x2,
在Rt△BCE中,
CE2=BC2+BE2=152+(25﹣x)2,
由题意可知:DE=CE,
所以:102+x2=152+(25﹣x)2,
解得:x=15km.
所以,E应建在距A点15km处.
故选:C.
30.解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.
在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B2,
∴BD2+22=6.25,
∴BD2=2.25,
∵BD>0,
∴BD=1.5米,
∴CD=BC+BD=0.7+1.5=2.2米.
故选:A.
31.解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,即BC=CA,设AC为x,则OC=45﹣x,
由勾股定理可知OB2+OC2=BC2,
又∵OA=45,OB=15,
把它代入关系式152+(45﹣x)2=x2,
解方程得出x=25(cm).
答:如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是25cm.
32.解:(1)在Rt△ABC中,∠CAB=90°,BC=13m,AC=5m,
∴(m),
故答案为:12;
(2)∵淇淇收绳5m后,船到达D处,
∴CD=8(m),
∴AD=(m),
∴BD=AB﹣AD=(12﹣)m.
故答案为:(12﹣).
33.解:(1)∵AC的长度是男孩未拽之前的绳子长,(BC+CE)的长度是男孩拽之后的绳子长,绳长始终保持不变,
∴AC=BC+CE,
故答案为:=;
(2)连接AB,如图所示:
则点A、B、F三点共线,
在Rt△CFA中,由勾股定理得:AC===13(米),
∵BF=AF﹣AB=12﹣9=3(米),
在Rt△CFB中,由勾股定理得:BC===(米),
由(1)得:AC=BC+CE,
∴CE=AC﹣BC=(13﹣)(米),
∴小男孩需向右移动的距离为(13﹣)米.
34.解:(1)在直角△ABC中,已知AC=30米,AB=50米,
且AB为斜边,则BC==40米.
答:小汽车在2秒内行驶的距离BC为40米;
(2)小汽车在2秒内行驶了40米,所以平均速度为20米/秒,
20米/秒=72千米/时,
因为72>70,
所以这辆小汽车超速了.
答:这辆小汽车的平均速度大于70千米/时,故这辆小汽车超速了.
35.解:公路AB需要暂时封锁.
理由如下:如图,过C作CD⊥AB于D.
因为BC=400米,AC=300米,∠ACB=90°,
所以根据勾股定理有AB=500米.
因为S△ABC=AB CD=BC AC
所以CD===240米.
由于240米<250米,故有危险,
因此AB段公路需要暂时封锁.
36.解:(1)∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)海港C受台风影响,
理由:过点C作CD⊥AB,
∵△ABC是直角三角形,
∴AC×BC=CD×AB,
∴300×400=500×CD,
∴CD=240(km),
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受台风影响;
(3)当EC=250km,FC=250km时,正好影响C港口,
∵ED==70(km),
∴EF=140km,
∵台风的速度为20千米/小时,
∴140÷20=7(小时).
答:台风影响该海港持续的时间为7小时.
37.解:连接AC,在Rt△ABC中,AB=3米,BC=4米,
∵AC2=AB2+BC2=32+42=25,
∴AC=5,
∵AC2+AD2=52+122=169,CD2=132=169,
∴AC2+AD2=CD2,
∴∠DAC=90°,
该区域面积=S△ACD﹣S△ABC=30﹣6=24(平方米),
铺满这块空地共需花费=24×80=1920(元).
答:用该草坪铺满这块空地共需花费1920元.
38.解:(1)如图,连接AC,
在Rt△ABC中,∵AB=3m,BC=4m,∠B=90°,AB2+CB2=AC2
∴AC=5cm,
在△ACD中,AC=5cmCD=12m,DA=13m,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°;
(2)∵S△ABC=×3×4=6,S△ACD=×5×12=30,
∴S四边形ABCD=6+30=36,
费用=36×80=2880(元).
答:铺满这块空地共需花费2880元.
39.解:(1)学校受到噪音影响.理由如下:
作AB⊥MN于B,如图1,
∵PA=120m,∠QPN=30°,
∴AB=PA=60m,
而60m<100m,
∴消防车在公路MN上沿PN方向行驶时,学校受到噪音影响;
(2)以点A为圆心,100m为半径作⊙A交MN于C、D,如图,
∵AB⊥CD,
∴CB=BD,
在Rt△ABC中,AC=100m,AB=60m,
CB==80m,
∴CD=2BC=160m,
∵消防车的速度5m/s,
∴消防车在线段CD上行驶所需要的时间=160÷5=32(秒),
∴学校受影响的时间为32秒.
40.解:∵甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行,
∴AO⊥BO,
∵甲以20海里/时的速度向南偏东45°方向航行,
∴OB=20×2=40(海里),
∵AB=50海里,
在Rt△AOB中,,
∴乙轮船平均每小时航行30÷2=15海里.
