2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.1.2全概率公式课件(21张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.1.2全概率公式课件(21张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 15:49:20 | ||
图片预览







文档简介
第七章 随机变量及其分布
7.1条件概率与全概率公式
7.1.2 全概率公式
贝叶斯公式也称为贝叶斯法则, 尽管它是一个数学公式,但其原理毋需数字也可明了.如果你看到一个人总是做一些好事,则那个人多半会是一个好人.这就是说,当你不能准确知悉一个事物的本质时,你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率.用数学语言表达就是:支持某项属性的事件发生得愈多,则该属性成立的可能性就愈大.
学习目标
1.结合古典概型,了解利用概率的加法公式和乘法公式推导出全概率公式的过程;
2.理解全概率公式的形式并会利用全概率公式计算概率;
3.了解贝叶斯公式以及公式的简单应用.
问题导学
在上节计算按对银行储蓄卡密码的概率时,我们首先把一个复杂事件表示为一些简单事件运算的结果,然后利用概率的加法公式和乘法公式求其概率,下面我们再看一个求复杂事件概率的问题.
?
?
P(R2|R1)
P(B2|R1)
P(R2|B1)
P(B2|B1)
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
新知探究
知识概念
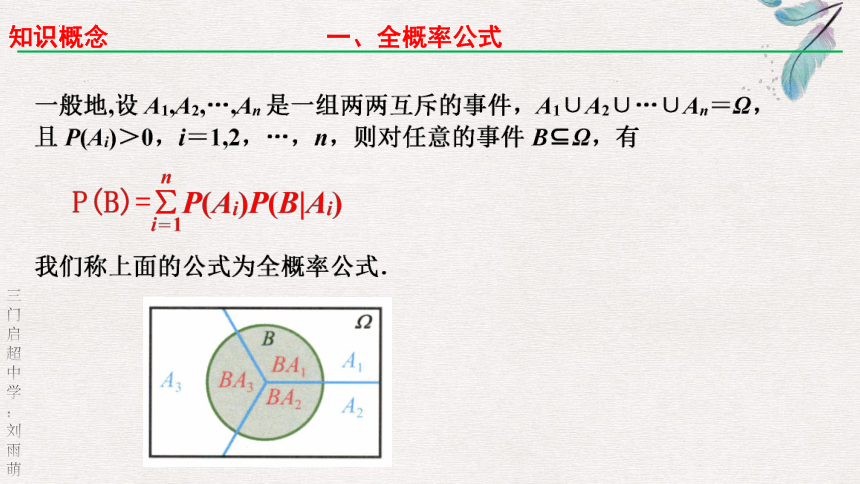
一、全概率公式
例1. 某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率.
分析:第2天去哪家餐厅用餐的概率受第1天在哪家餐厅用餐的影响,可根据第1天可能去的餐厅,将样本空间表示为“第1天去A餐厅”和“第1天去B餐厅”两个互斥事件的并,利用全概率公式求解.
典例分析
?
全品79页例1 全概率公式的运用
典例分析
例1 已知甲袋中有3个白球和2个黑球,乙袋中有4个白球和4个黑球.现从甲袋中任取2个球放入乙袋,然后再从乙袋中任取1个球,求此球为白球的概率.
?
归纳总结
全概率公式针对的是某一个过程中已知条件求结果发生的概率,解题步骤
如下:
(1)按照某种标准将条件事件分解为n个彼此互斥事件的并,将这n个事件分别命名为Ai(i=1,2,…,n);
(2)命名目标的概率事件为事件B;
(3)分别计算P(Ai)P(B|Ai);
(4)代入全概率公式求解.
例2. (教材例5)有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
典例分析
分析:取到的零件可能来自第1台车床,也可能来自第2台或第3台车床,有3种可能.设B=“任取一零件为次品”,Ai=“零件为第i台车床加工”(i=1,2,3),如图所示,可将事件B表示为3个两两互斥事件的并,利用全概率公式可以计算出事件B的概率.
教材50页例5
?
(1)由全概率公式,得
P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+ P(A3)P(B|A3)
=0.25×0.06+0.3×0.05+0.45×0.05=0.0525
?
问题2:例5中P(Ai), P(Ai|B)得实际意义是什么?
?
解题反思
*贝叶斯公式:
知识概念
二、贝叶斯公式
典例分析
全品79页例2 贝叶斯公式的应用*
例2 甲盒装有1个白球和2个黑球,乙盒装有3个白球和2个黑球,丙盒装有4个白球和1个黑球.采取掷骰子的方法决定选盒,出现1,2或3点选甲盒,出现4,5点选乙盒,出现6点选丙盒,在选出的盒里随机摸出1个球,已知摸得1个白球,求此球来自乙盒的概率.
?
归纳小结
?
练习(教材例2. )在数字通信中,信号是由数字0和1组成的序列。由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05.假设发送信号0和1是等可能的.
典例分析
(1)分别求接收的信号为0和1的概率;
*(2)已知接收的信号为0,求发送的信号是1的概率.
分析:设A=“发送的信号为0”,B=“接收到的信号为0”.为便于求解,我们可将目中所包含的各种信息用图直观表示.
发送0(A)
发送1(????)
?
接收0(B)
接收1(????)
?
????????|????=????.????
?
????????|????=????.????
?
????????|????=????.????????
?
????????|????=????.????????
?
教材51页例2
?
?
?
?
发送0(A)
发送1(????)
?
接收0(B)
接收1(????)
?
????????|????=????.????
?
????????|????=????.????
?
????????|????=????.????????
?
????????|????=????.????????
?
如果随机试验可以看成两个阶段,且第一阶段的各试验结果具体结果未知,那么:
(1)若要求的是第二阶段某一个结果发生的概率,则用全概率公式;
(2)若第二个阶段的某一个结果是已知的,要求的是此结果为第一阶段某一个结果所引起的概率,一般用贝叶斯公式,类似于求条件概率. 熟记这个特征,在遇到相关的题目时,可以准确地选择方法进行计算,保证解题的正确高效.
课堂小结——你学到了那些新知识呢?
课后作业
课后作业全品23-24页1-14必做,15-17选做.
7.1条件概率与全概率公式
7.1.2 全概率公式
贝叶斯公式也称为贝叶斯法则, 尽管它是一个数学公式,但其原理毋需数字也可明了.如果你看到一个人总是做一些好事,则那个人多半会是一个好人.这就是说,当你不能准确知悉一个事物的本质时,你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率.用数学语言表达就是:支持某项属性的事件发生得愈多,则该属性成立的可能性就愈大.
学习目标
1.结合古典概型,了解利用概率的加法公式和乘法公式推导出全概率公式的过程;
2.理解全概率公式的形式并会利用全概率公式计算概率;
3.了解贝叶斯公式以及公式的简单应用.
问题导学
在上节计算按对银行储蓄卡密码的概率时,我们首先把一个复杂事件表示为一些简单事件运算的结果,然后利用概率的加法公式和乘法公式求其概率,下面我们再看一个求复杂事件概率的问题.
?
?
P(R2|R1)
P(B2|R1)
P(R2|B1)
P(B2|B1)
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
新知探究
知识概念
一、全概率公式
例1. 某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率.
分析:第2天去哪家餐厅用餐的概率受第1天在哪家餐厅用餐的影响,可根据第1天可能去的餐厅,将样本空间表示为“第1天去A餐厅”和“第1天去B餐厅”两个互斥事件的并,利用全概率公式求解.
典例分析
?
全品79页例1 全概率公式的运用
典例分析
例1 已知甲袋中有3个白球和2个黑球,乙袋中有4个白球和4个黑球.现从甲袋中任取2个球放入乙袋,然后再从乙袋中任取1个球,求此球为白球的概率.
?
归纳总结
全概率公式针对的是某一个过程中已知条件求结果发生的概率,解题步骤
如下:
(1)按照某种标准将条件事件分解为n个彼此互斥事件的并,将这n个事件分别命名为Ai(i=1,2,…,n);
(2)命名目标的概率事件为事件B;
(3)分别计算P(Ai)P(B|Ai);
(4)代入全概率公式求解.
例2. (教材例5)有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
典例分析
分析:取到的零件可能来自第1台车床,也可能来自第2台或第3台车床,有3种可能.设B=“任取一零件为次品”,Ai=“零件为第i台车床加工”(i=1,2,3),如图所示,可将事件B表示为3个两两互斥事件的并,利用全概率公式可以计算出事件B的概率.
教材50页例5
?
(1)由全概率公式,得
P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+ P(A3)P(B|A3)
=0.25×0.06+0.3×0.05+0.45×0.05=0.0525
?
问题2:例5中P(Ai), P(Ai|B)得实际意义是什么?
?
解题反思
*贝叶斯公式:
知识概念
二、贝叶斯公式
典例分析
全品79页例2 贝叶斯公式的应用*
例2 甲盒装有1个白球和2个黑球,乙盒装有3个白球和2个黑球,丙盒装有4个白球和1个黑球.采取掷骰子的方法决定选盒,出现1,2或3点选甲盒,出现4,5点选乙盒,出现6点选丙盒,在选出的盒里随机摸出1个球,已知摸得1个白球,求此球来自乙盒的概率.
?
归纳小结
?
练习(教材例2. )在数字通信中,信号是由数字0和1组成的序列。由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05.假设发送信号0和1是等可能的.
典例分析
(1)分别求接收的信号为0和1的概率;
*(2)已知接收的信号为0,求发送的信号是1的概率.
分析:设A=“发送的信号为0”,B=“接收到的信号为0”.为便于求解,我们可将目中所包含的各种信息用图直观表示.
发送0(A)
发送1(????)
?
接收0(B)
接收1(????)
?
????????|????=????.????
?
????????|????=????.????
?
????????|????=????.????????
?
????????|????=????.????????
?
教材51页例2
?
?
?
?
发送0(A)
发送1(????)
?
接收0(B)
接收1(????)
?
????????|????=????.????
?
????????|????=????.????
?
????????|????=????.????????
?
????????|????=????.????????
?
如果随机试验可以看成两个阶段,且第一阶段的各试验结果具体结果未知,那么:
(1)若要求的是第二阶段某一个结果发生的概率,则用全概率公式;
(2)若第二个阶段的某一个结果是已知的,要求的是此结果为第一阶段某一个结果所引起的概率,一般用贝叶斯公式,类似于求条件概率. 熟记这个特征,在遇到相关的题目时,可以准确地选择方法进行计算,保证解题的正确高效.
课堂小结——你学到了那些新知识呢?
课后作业
课后作业全品23-24页1-14必做,15-17选做.
