【2012参赛课件】数学:23《等差数列的前n项和》(新人教版必修5)
文档属性
| 名称 | 【2012参赛课件】数学:23《等差数列的前n项和》(新人教版必修5) |  | |
| 格式 | zip | ||
| 文件大小 | 274.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-18 09:36:16 | ||
图片预览






文档简介
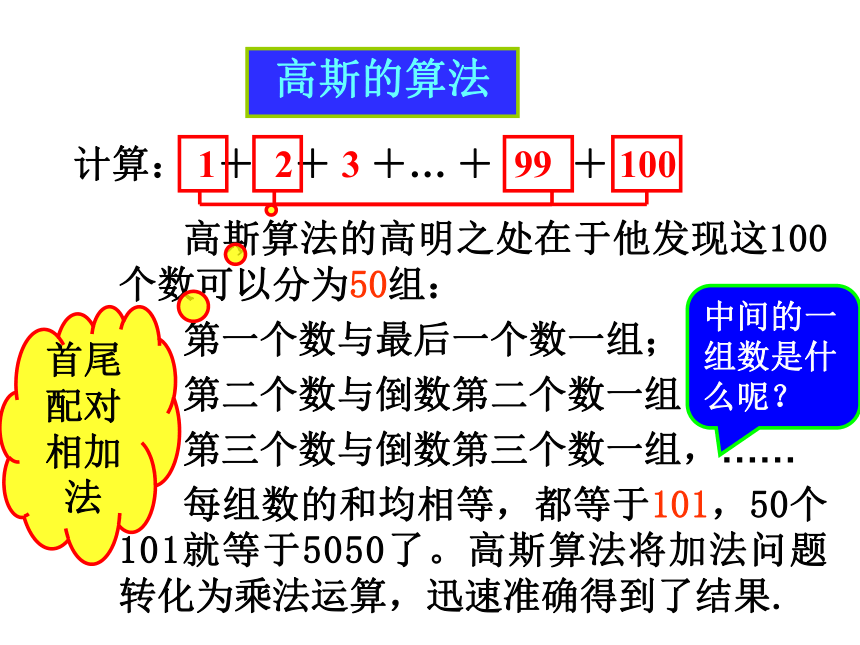
课件20张PPT。 有一次,老师与高斯去买铅笔,在商店发
现了一个堆放铅笔的V形架,
V形架的最下面一层放
一支铅笔,往上每一层
都比它下面一层多放一
支,最上面一层放100支.
老师问:高斯,你知道这
个V形架上共放着多少支铅笔吗?创设情景问题就是:计算1+ 2+ 3 +… + 99 + 100高斯(Gauss,1777—1855),德国著名数学家,他研究的内容涉及数学的各个领域,被称为历史上最伟大的三位数学家之一,他与阿基米德、牛顿齐名,是数学史上一颗光芒四射的巨星,被誉为“数学王子”.等差数列的前n项和胶南一中石锋学习要求:1、探索并掌握等差数列前n项和公式
2、学会用公式解决一些实际问题学习难点:等差数列前n项和公式推导思路的获得学习重点:1、知识目标
(1)掌握等差数列前n项和公式,理解公式的推导方法;
(2)能较熟练应用等差数列前n项和公式求和。
2、能力目标
经历公式的推导过程,体会数形结合的数学思想,体验从特殊到一般的研究方法,学会观察、归纳、反思和逻辑推理的能力。
3、情感目标
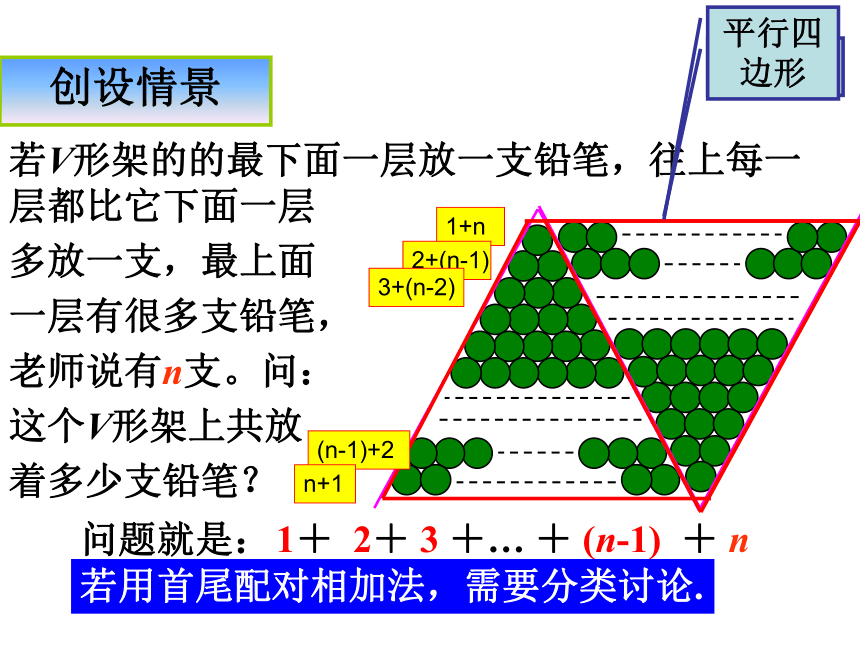
通过生动具体的现实问题,激发学生探究的兴趣和欲望,树立学生求真的勇气和自信心,增强学生学好数学的心理体验,产生热爱数学的情感,体验在学习中获得成功。高斯的算法计算: 1+ 2+ 3 +… + 99 + 100 高斯算法的高明之处在于他发现这100个数可以分为50组:
第一个数与最后一个数一组;
第二个数与倒数第二个数一组;
第三个数与倒数第三个数一组,……
每组数的和均相等,都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.首尾配对相加法中间的一组数是什么呢?若V形架的的最下面一层放一支铅笔,往上每一层都比它下面一层
多放一支,最上面
一层有很多支铅笔,
老师说有n支。问:
这个V形架上共放
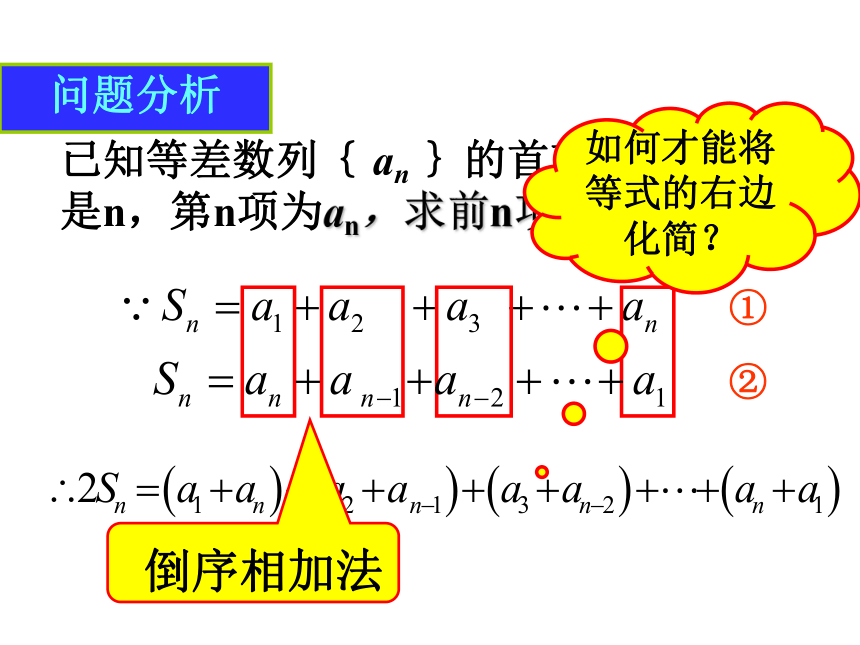
着多少支铅笔?创设情景问题就是:1+ 2+ 3 +… + (n-1) + n若用首尾配对相加法,需要分类讨论.三角形平行四边形1+n2+(n-1)3+(n-2)(n-1)+2n+1n + (n-1) + (n-2) +…+ 2 +1倒序相加法 那么,对一般的等差数列,如何求它的
前n项和呢?前n项和分析:这其实是求一个具体的等差数列前n项和.①②问题分析已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .如何才能将等式的右边化简?①②问题分析已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .任意的第K项与倒数第K项的和等于首项、末项的和求和公式等差数列的前n项和的公式:思考:(1)公式的文字语言;(2)公式的特点;不含d可知三求一等差数列的前n项和等于首末两项的和与项数乘积的一半。 想一想 在等差数列 {an} 中,如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 请问: 能否求出其余两个量 ?结论:知 三 求 二发现??公式应用1.根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=505002550答案: 272.例题讲解 例1、2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》,某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网。据测算,2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元。那么,从2001年起的未来10年内,该市在“校校通”工程中的总投入是多少?分析:①找关键句;②求什么,如何求;解:由题意,该市在“校校通”工程中每年投入的资金构成等差数列{an},且a1=500,d=50,n=10.故,该市在未来10年内的总投入为:答变式练习 一个屋顶的某一斜面成等腰梯形,最上面一层铺瓦片21块,往下每一层多铺1块,斜面上铺了19层,共铺瓦片多少块?解:由题意,该屋顶斜面每层所铺的瓦片数构成等差数列{an},且a1=21,d=1,n=19.于是,屋顶斜面共铺瓦片:答:屋顶斜面共铺瓦片570块.例题讲解例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗? 分析:将已知条件代入等差数列前n项和的公式后,可得到两个关于 与d的二元一次方程,由此可以求得 与d,从而得到所求前n项和的公式. 解:由题意知 ,将它们代入公式 解这个关于a1与d的方程组,得到 a1 =4,d=6 得到所以巩固训练1.2. B接轨高考 【命题立意】
考查等差数列的前n项和公式以及基本计算.自我检测C课堂小结 1.等差数列前n项和的公式;
2.等差数列前n项和公式的推导方法——倒序相加法;数学发现的方法:学会猜想,学会证明
3.在两个求和公式中,各有五个元素,只要知道其中三个元素,结合通项公式就
可求出另两个元素.
思想运用:方程思想
(两个)an=a1+(n-1)d对于Sn、an 、a1、n、d 五个量,“知三求二”.方程(组)思想
(待定系数法)倒序求和法 掌握与应用谢 谢!让过程更加美丽!
让结果更加灿烂!
现了一个堆放铅笔的V形架,
V形架的最下面一层放
一支铅笔,往上每一层
都比它下面一层多放一
支,最上面一层放100支.
老师问:高斯,你知道这
个V形架上共放着多少支铅笔吗?创设情景问题就是:计算1+ 2+ 3 +… + 99 + 100高斯(Gauss,1777—1855),德国著名数学家,他研究的内容涉及数学的各个领域,被称为历史上最伟大的三位数学家之一,他与阿基米德、牛顿齐名,是数学史上一颗光芒四射的巨星,被誉为“数学王子”.等差数列的前n项和胶南一中石锋学习要求:1、探索并掌握等差数列前n项和公式
2、学会用公式解决一些实际问题学习难点:等差数列前n项和公式推导思路的获得学习重点:1、知识目标
(1)掌握等差数列前n项和公式,理解公式的推导方法;
(2)能较熟练应用等差数列前n项和公式求和。
2、能力目标
经历公式的推导过程,体会数形结合的数学思想,体验从特殊到一般的研究方法,学会观察、归纳、反思和逻辑推理的能力。
3、情感目标
通过生动具体的现实问题,激发学生探究的兴趣和欲望,树立学生求真的勇气和自信心,增强学生学好数学的心理体验,产生热爱数学的情感,体验在学习中获得成功。高斯的算法计算: 1+ 2+ 3 +… + 99 + 100 高斯算法的高明之处在于他发现这100个数可以分为50组:
第一个数与最后一个数一组;
第二个数与倒数第二个数一组;
第三个数与倒数第三个数一组,……
每组数的和均相等,都等于101,50个101就等于5050了。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.首尾配对相加法中间的一组数是什么呢?若V形架的的最下面一层放一支铅笔,往上每一层都比它下面一层
多放一支,最上面
一层有很多支铅笔,
老师说有n支。问:
这个V形架上共放
着多少支铅笔?创设情景问题就是:1+ 2+ 3 +… + (n-1) + n若用首尾配对相加法,需要分类讨论.三角形平行四边形1+n2+(n-1)3+(n-2)(n-1)+2n+1n + (n-1) + (n-2) +…+ 2 +1倒序相加法 那么,对一般的等差数列,如何求它的
前n项和呢?前n项和分析:这其实是求一个具体的等差数列前n项和.①②问题分析已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .如何才能将等式的右边化简?①②问题分析已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .任意的第K项与倒数第K项的和等于首项、末项的和求和公式等差数列的前n项和的公式:思考:(1)公式的文字语言;(2)公式的特点;不含d可知三求一等差数列的前n项和等于首末两项的和与项数乘积的一半。 想一想 在等差数列 {an} 中,如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 请问: 能否求出其余两个量 ?结论:知 三 求 二发现??公式应用1.根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=505002550答案: 272.例题讲解 例1、2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》,某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网。据测算,2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元。那么,从2001年起的未来10年内,该市在“校校通”工程中的总投入是多少?分析:①找关键句;②求什么,如何求;解:由题意,该市在“校校通”工程中每年投入的资金构成等差数列{an},且a1=500,d=50,n=10.故,该市在未来10年内的总投入为:答变式练习 一个屋顶的某一斜面成等腰梯形,最上面一层铺瓦片21块,往下每一层多铺1块,斜面上铺了19层,共铺瓦片多少块?解:由题意,该屋顶斜面每层所铺的瓦片数构成等差数列{an},且a1=21,d=1,n=19.于是,屋顶斜面共铺瓦片:答:屋顶斜面共铺瓦片570块.例题讲解例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗? 分析:将已知条件代入等差数列前n项和的公式后,可得到两个关于 与d的二元一次方程,由此可以求得 与d,从而得到所求前n项和的公式. 解:由题意知 ,将它们代入公式 解这个关于a1与d的方程组,得到 a1 =4,d=6 得到所以巩固训练1.2. B接轨高考 【命题立意】
考查等差数列的前n项和公式以及基本计算.自我检测C课堂小结 1.等差数列前n项和的公式;
2.等差数列前n项和公式的推导方法——倒序相加法;数学发现的方法:学会猜想,学会证明
3.在两个求和公式中,各有五个元素,只要知道其中三个元素,结合通项公式就
可求出另两个元素.
思想运用:方程思想
(两个)an=a1+(n-1)d对于Sn、an 、a1、n、d 五个量,“知三求二”.方程(组)思想
(待定系数法)倒序求和法 掌握与应用谢 谢!让过程更加美丽!
让结果更加灿烂!
