【2012参赛课件】数学:231双曲线及其标准方程 新人教A版选修2-1
文档属性
| 名称 | 【2012参赛课件】数学:231双曲线及其标准方程 新人教A版选修2-1 |

|
|
| 格式 | zip | ||
| 文件大小 | 377.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-18 00:00:00 | ||
图片预览







文档简介
课件22张PPT。2.3.1 双曲线及其标准方程2012年12月6日椭圆的定义?创设情境···新课引入平面内与两个定点F1、F2的
距离的和等于常数(大于|F1F2|)
的点轨迹叫做椭圆。思考:如果把椭圆定义中的“距离之和”改为“距离之差”,那么点的轨迹是怎样的曲线?
即“平面内与两个定点F1、F2的距离的差等于常数的点的轨迹 ”是什么?
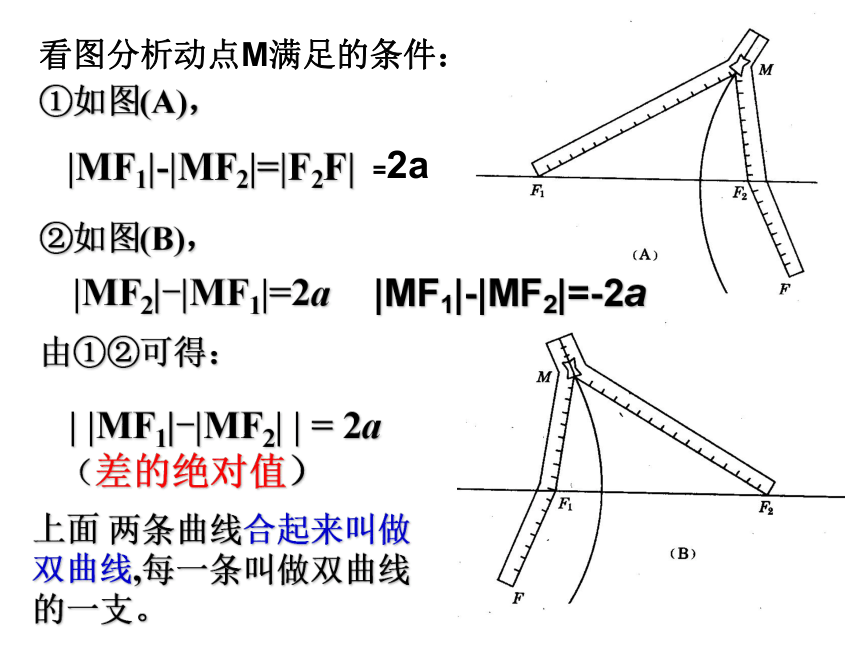
①如图(A), |MF1|-|MF2|=|F2F|②如图(B),|MF2|-|MF1|=2a由①②可得: | |MF1|-|MF2| | = 2a
(差的绝对值)上面 两条曲线合起来叫做
双曲线,每一条叫做双曲线
的一支。看图分析动点M满足的条件:=2a|MF1|-|MF2|=-2a学习目标1、知识与技能目标
记住双曲线的定义,几何图形及标准方程。
2、过程与方法目标
类比椭圆的定义、标准方程,得到双曲线的定义, 标准方程,并注意两者的比较。
3、情感、态度价值观目标
体会运动变化的观点,数形结合的思想及类比的方法,体会几何图形的简洁美,对称美,和谐美。教学重点、难点、关键重点:双曲线的定义与简单应用
难点:双曲线标准方程的推导
教学关键:利用类比、联想、对比等手段得出双曲线的定义及标准方程。探究1常数2a满足什么条件时才为双曲线?(5)常数0<2a<|F1F2|时,动点的轨迹才是双曲线双曲线的定义 平面内与两个定点F1,F2的距离的差的绝对值等于常数2a 的点的轨迹叫做双曲线.(小于︱F1F2︱)① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距. 显然0<2a<2c分层练习·当堂达标以(-5,0),(5,0)为焦点的双曲线双曲线的右支 设M(x , y),双曲线的焦
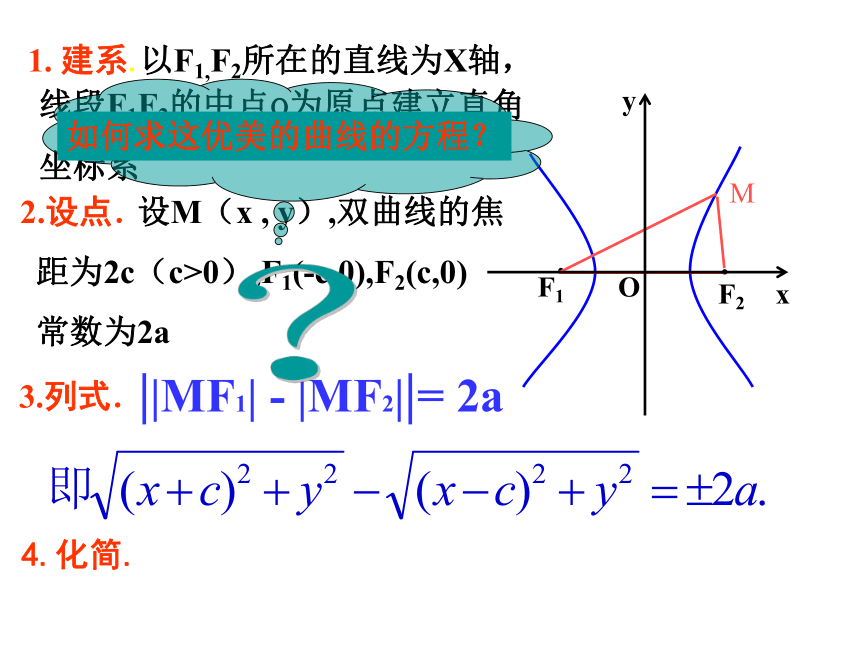
距为2c(c>0),F1(-c,0),F2(c,0)
常数为2aM 以F1,F2所在的直线为X轴,线段F1F2的中点o为原点建立直角
坐标系1. 建系.2.设点.3.列式.||MF1| - |MF2||= 2a4.化简.F1F2令 c2-a2 =b2
想一想:这与椭圆中的关系一样吗?焦点在X轴上的双曲线的标准方程五:说明双曲线上任意一点的坐标都满足方程;以方程的解(x,y)为坐标的点都在双曲线上
由曲线与方程的关系可知,方程就是双曲线的方程。你能在Y轴上找一点B使得OB的长度为b吗?探究2焦点在y轴上的双曲线的标准方程是什么?想一想F1 (0,-c) , F2 (0,c) ,M(x,y)建系设点列式化简方程焦点a.b.c 的关系图象定义| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F(0, ± c)焦点在X轴上焦点在Y轴上F ( ±c, 0)焦点位置如何判断双曲线的焦点在哪个轴上?写出以下双曲线的焦点坐标 椭圆以大小论长短,双曲线以正负定实虚看 前的系数,哪一个为正,则在哪一个轴上探究3练习2典例剖析巩固练习求适合下列条件的双曲线的标准方程
①a=4,b=3,焦点在x轴上;
②焦距为12,a=3的双曲线标准方程;变式: 上述方程表示双曲线,则m的取值范围是
__________________m<-2或m>-1例2已知方程 表示焦点在y轴的
双曲线,则实数m的取值范围是______________m<-2典例剖析F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)椭圆以大小论长短双曲线以正负定实虚1、双曲线及其焦点,焦距的定义,双曲线的标准方程 以及方程中的a、b、c之间的关系课堂小结:2、焦点位置的确定方法3、求双曲线标准方程关键(定位,定量)知识方面思想方法、规律方面数形结合、类比推理、归纳推理、待定系数法等课后反思针对本节课学习的内容、方法、规律记下你的收获:
通过本节课的学习,记下你的困惑,以备课下讨论或询问老师!作业布置一、书面作业:课本P55,第1题
要求:书写具体解题过程二、课后练习:导学案(剩余部分)三、课后探究:双曲线在日常生活中的应用(GPS(全球定位系统))、在光学中的应用等。谢谢指导
距离的和等于常数(大于|F1F2|)
的点轨迹叫做椭圆。思考:如果把椭圆定义中的“距离之和”改为“距离之差”,那么点的轨迹是怎样的曲线?
即“平面内与两个定点F1、F2的距离的差等于常数的点的轨迹 ”是什么?
①如图(A), |MF1|-|MF2|=|F2F|②如图(B),|MF2|-|MF1|=2a由①②可得: | |MF1|-|MF2| | = 2a
(差的绝对值)上面 两条曲线合起来叫做
双曲线,每一条叫做双曲线
的一支。看图分析动点M满足的条件:=2a|MF1|-|MF2|=-2a学习目标1、知识与技能目标
记住双曲线的定义,几何图形及标准方程。
2、过程与方法目标
类比椭圆的定义、标准方程,得到双曲线的定义, 标准方程,并注意两者的比较。
3、情感、态度价值观目标
体会运动变化的观点,数形结合的思想及类比的方法,体会几何图形的简洁美,对称美,和谐美。教学重点、难点、关键重点:双曲线的定义与简单应用
难点:双曲线标准方程的推导
教学关键:利用类比、联想、对比等手段得出双曲线的定义及标准方程。探究1常数2a满足什么条件时才为双曲线?(5)常数0<2a<|F1F2|时,动点的轨迹才是双曲线双曲线的定义 平面内与两个定点F1,F2的距离的差的绝对值等于常数2a 的点的轨迹叫做双曲线.(小于︱F1F2︱)① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距. 显然0<2a<2c分层练习·当堂达标以(-5,0),(5,0)为焦点的双曲线双曲线的右支 设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数为2aM 以F1,F2所在的直线为X轴,线段F1F2的中点o为原点建立直角
坐标系1. 建系.2.设点.3.列式.||MF1| - |MF2||= 2a4.化简.F1F2令 c2-a2 =b2
想一想:这与椭圆中的关系一样吗?焦点在X轴上的双曲线的标准方程五:说明双曲线上任意一点的坐标都满足方程;以方程的解(x,y)为坐标的点都在双曲线上
由曲线与方程的关系可知,方程就是双曲线的方程。你能在Y轴上找一点B使得OB的长度为b吗?探究2焦点在y轴上的双曲线的标准方程是什么?想一想F1 (0,-c) , F2 (0,c) ,M(x,y)建系设点列式化简方程焦点a.b.c 的关系图象定义| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F(0, ± c)焦点在X轴上焦点在Y轴上F ( ±c, 0)焦点位置如何判断双曲线的焦点在哪个轴上?写出以下双曲线的焦点坐标 椭圆以大小论长短,双曲线以正负定实虚看 前的系数,哪一个为正,则在哪一个轴上探究3练习2典例剖析巩固练习求适合下列条件的双曲线的标准方程
①a=4,b=3,焦点在x轴上;
②焦距为12,a=3的双曲线标准方程;变式: 上述方程表示双曲线,则m的取值范围是
__________________m<-2或m>-1例2已知方程 表示焦点在y轴的
双曲线,则实数m的取值范围是______________m<-2典例剖析F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)椭圆以大小论长短双曲线以正负定实虚1、双曲线及其焦点,焦距的定义,双曲线的标准方程 以及方程中的a、b、c之间的关系课堂小结:2、焦点位置的确定方法3、求双曲线标准方程关键(定位,定量)知识方面思想方法、规律方面数形结合、类比推理、归纳推理、待定系数法等课后反思针对本节课学习的内容、方法、规律记下你的收获:
通过本节课的学习,记下你的困惑,以备课下讨论或询问老师!作业布置一、书面作业:课本P55,第1题
要求:书写具体解题过程二、课后练习:导学案(剩余部分)三、课后探究:双曲线在日常生活中的应用(GPS(全球定位系统))、在光学中的应用等。谢谢指导
