【2012参赛课件】数学:111《算法的概念》(新人教A版必修3)
文档属性
| 名称 | 【2012参赛课件】数学:111《算法的概念》(新人教A版必修3) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-18 09:38:55 | ||
图片预览





文档简介
课件17张PPT。1.1.1算法的概念(新人教A版必修3)1.1算法的概念教学目的:
1、知道算法的概念,掌握算法的基本特点
2、能读懂自然语言描述的算法
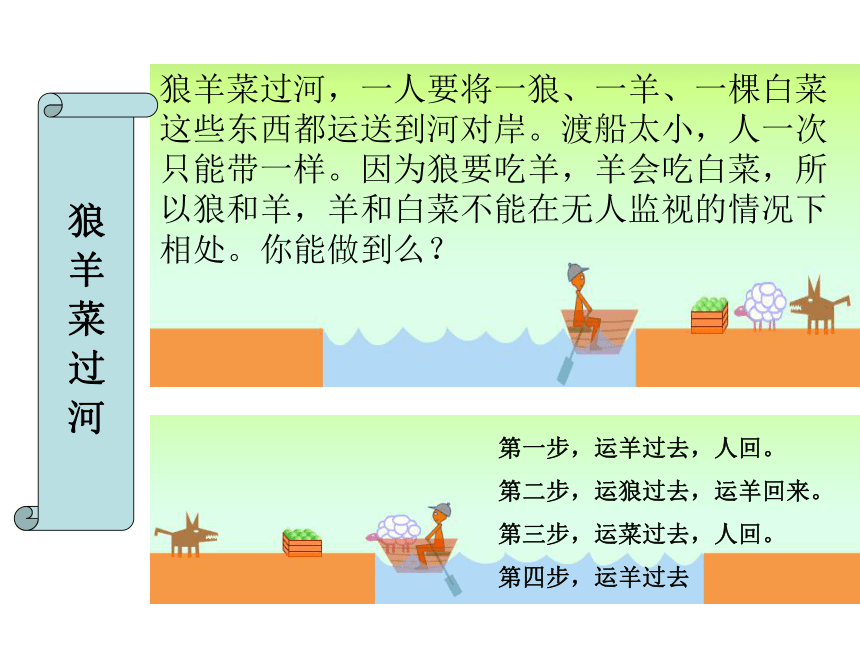
3、体会算法的基本思想,会写一些简单的算法步骤教学重点、难点:重点:通过分析解决具体问题的过程和步骤,体会算法的思想,能用简单的自然语言描述解决具体问题的算法。难点:用算法步骤表示算法是怎样划分步骤 狼羊菜过河,一人要将一狼、一羊、一棵白菜这些东西都运送到河对岸。渡船太小,人一次只能带一样。因为狼要吃羊,羊会吃白菜,所以狼和羊,羊和白菜不能在无人监视的情况下相处。你能做到么? 第一步,运羊过去,人回。
第二步,运狼过去,运羊回来。
第三步,运菜过去,人回。
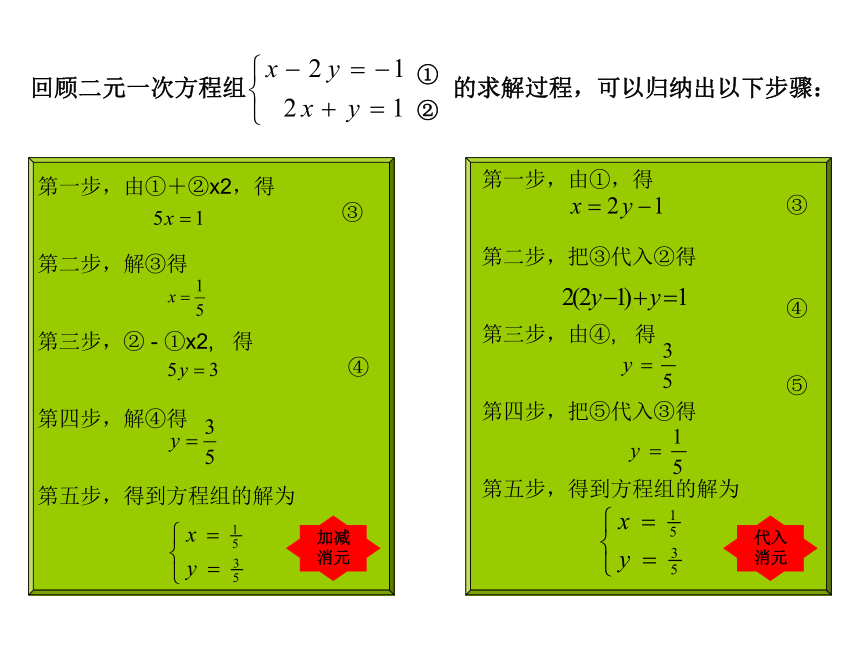
第四步,运羊过去 狼 羊 菜 过 河 写出求解一般的二元一次方程组的解的步骤.算法的概念和特征2、特征:(1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的.
(2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.
(3)逻辑性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题.
(4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法.1、概念:通常指按照一定规则解决某一类问题的明确的和有限的步骤。(早期,用阿拉伯数字进行算术运算的过程;现在,算法通常可以编成程序,让计算机执行并解决问题。)1)设计一个算法,判断7是否为质数
2)设计一个算法,判断35是否是质数算法分析:
根据质数的定义,依次用2-6除7,如果它们中的一个能整除7,则7不是质数,否则7是质数,类似地,可以写出“35是否是质数”的算法2)类似地,可以写出“35是否是质数”的算法:
第一步:用2除35得到余数1,因为余数1不为0,所 以不能被2整除
第二步:用3除35得到余数2,因为余数2不为0,所以不能被3整除
第三步:用4除35得到余数3,因为余数3不为0,所以不能被4整除
第四步:用5除35得到余数0,因为余数为0,所以能被5整除,则35不是质数。任意给定一个大于2的整数n,试设计一个判断 n是否为质数的算法.算法分析:对于任意的整数n(n>2),若用i表示2—(n-1)中的任意整数,则判断整数n(n>2)是否为质数的算法包含下面的重复操作。
用i除n,得到余数r,判断余数r是否为0,若是,则n不是质数;否则,将i的值增加1.再执行同样的操作.这个操作一直要进行到i的值等于(n-1)为止。能力提升第一步:给定正整数n
第二步:令i=2
第三步:用i除n,得到余数r
第四步:判断“r=0”是否成立,若是则n不是质数,结束算法,否则将i的值增加1
第五步:判断“i>(n-1)”是否成立,若是,则n是质数,结束算法,否则返回第四步算法分析:令f(x)= x2-2=0(x>0),则方程x2-2=0的解就是函数f(x)的零点.
二分法的基本思想是:把函数f(x)的零点所在的区间[a,b](满足f(a)f(b)<0)一分为二,得到[a,m]和[m,b].根据f(a)f(m)<0是否成立,取出零点所在的区间[a,m]或[m,b],仍记为[a,b].对所得的区间[a,b],重复上述步骤,直到包含零点的区间[a,b]足够小,则[a,b]内的数可以作为方程的近似解.
写出用“二分法”求方程x2-2=0(x>0)的近似解的算法.第一步,令f(x)= x2-2=0,给出精确度d.
第二步,确定区间[a,b],满足f(a)f(b)<0.
第三步,取区间中点m=(a+b)/2.
第四步,若f(a)f(m)<0,则含零点的区间
为[a,m];否则 ,含零点的区间为
[m,b].将新得到的含零点的区间
仍记为[a,b].
第五步,判断[a,b]的长度是否小于d或f(m)
是否等于0.若是,则m是方程的近
似解;否则,返回第三步.
可以写出算法:
根据以上分析,任意给定一个大于1的正整数n,试设计一个算法求出n的所有因数。第一步:给定一个大于1的正整数 n
第二步:令 i=1
第三步:用 i 除 n 得余数 r
第四步:判断“ r=0 ”是否成立:若是,则 i 是 n 的因数;
否则, i 不是 n 的因数
第五步:使 i 的值增加1,仍用 i 表示
第六步:判断“ i>n-1 ” 是否成立:若是,则结束算法;
否则,返回第三步【小结】
算法的思想和初步知识,正在成为普通公民的常识,成为现代人应具备的一种基本数学素养。
本节通过实例引出了算法的概念进而总结了算法的特征,主要学习了:求解二元一次方程组的算法;判断n是否为质数的算法;二分法求解方程的近似解的算法.通过学习这些案例,体会算法的特点,初步感受算法思想,体会算法的基本逻辑结构,提升逻辑思维能力。
1、知道算法的概念,掌握算法的基本特点
2、能读懂自然语言描述的算法
3、体会算法的基本思想,会写一些简单的算法步骤教学重点、难点:重点:通过分析解决具体问题的过程和步骤,体会算法的思想,能用简单的自然语言描述解决具体问题的算法。难点:用算法步骤表示算法是怎样划分步骤 狼羊菜过河,一人要将一狼、一羊、一棵白菜这些东西都运送到河对岸。渡船太小,人一次只能带一样。因为狼要吃羊,羊会吃白菜,所以狼和羊,羊和白菜不能在无人监视的情况下相处。你能做到么? 第一步,运羊过去,人回。
第二步,运狼过去,运羊回来。
第三步,运菜过去,人回。
第四步,运羊过去 狼 羊 菜 过 河 写出求解一般的二元一次方程组的解的步骤.算法的概念和特征2、特征:(1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的.
(2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.
(3)逻辑性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题.
(4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法.1、概念:通常指按照一定规则解决某一类问题的明确的和有限的步骤。(早期,用阿拉伯数字进行算术运算的过程;现在,算法通常可以编成程序,让计算机执行并解决问题。)1)设计一个算法,判断7是否为质数
2)设计一个算法,判断35是否是质数算法分析:
根据质数的定义,依次用2-6除7,如果它们中的一个能整除7,则7不是质数,否则7是质数,类似地,可以写出“35是否是质数”的算法2)类似地,可以写出“35是否是质数”的算法:
第一步:用2除35得到余数1,因为余数1不为0,所 以不能被2整除
第二步:用3除35得到余数2,因为余数2不为0,所以不能被3整除
第三步:用4除35得到余数3,因为余数3不为0,所以不能被4整除
第四步:用5除35得到余数0,因为余数为0,所以能被5整除,则35不是质数。任意给定一个大于2的整数n,试设计一个判断 n是否为质数的算法.算法分析:对于任意的整数n(n>2),若用i表示2—(n-1)中的任意整数,则判断整数n(n>2)是否为质数的算法包含下面的重复操作。
用i除n,得到余数r,判断余数r是否为0,若是,则n不是质数;否则,将i的值增加1.再执行同样的操作.这个操作一直要进行到i的值等于(n-1)为止。能力提升第一步:给定正整数n
第二步:令i=2
第三步:用i除n,得到余数r
第四步:判断“r=0”是否成立,若是则n不是质数,结束算法,否则将i的值增加1
第五步:判断“i>(n-1)”是否成立,若是,则n是质数,结束算法,否则返回第四步算法分析:令f(x)= x2-2=0(x>0),则方程x2-2=0的解就是函数f(x)的零点.
二分法的基本思想是:把函数f(x)的零点所在的区间[a,b](满足f(a)f(b)<0)一分为二,得到[a,m]和[m,b].根据f(a)f(m)<0是否成立,取出零点所在的区间[a,m]或[m,b],仍记为[a,b].对所得的区间[a,b],重复上述步骤,直到包含零点的区间[a,b]足够小,则[a,b]内的数可以作为方程的近似解.
写出用“二分法”求方程x2-2=0(x>0)的近似解的算法.第一步,令f(x)= x2-2=0,给出精确度d.
第二步,确定区间[a,b],满足f(a)f(b)<0.
第三步,取区间中点m=(a+b)/2.
第四步,若f(a)f(m)<0,则含零点的区间
为[a,m];否则 ,含零点的区间为
[m,b].将新得到的含零点的区间
仍记为[a,b].
第五步,判断[a,b]的长度是否小于d或f(m)
是否等于0.若是,则m是方程的近
似解;否则,返回第三步.
可以写出算法:
根据以上分析,任意给定一个大于1的正整数n,试设计一个算法求出n的所有因数。第一步:给定一个大于1的正整数 n
第二步:令 i=1
第三步:用 i 除 n 得余数 r
第四步:判断“ r=0 ”是否成立:若是,则 i 是 n 的因数;
否则, i 不是 n 的因数
第五步:使 i 的值增加1,仍用 i 表示
第六步:判断“ i>n-1 ” 是否成立:若是,则结束算法;
否则,返回第三步【小结】
算法的思想和初步知识,正在成为普通公民的常识,成为现代人应具备的一种基本数学素养。
本节通过实例引出了算法的概念进而总结了算法的特征,主要学习了:求解二元一次方程组的算法;判断n是否为质数的算法;二分法求解方程的近似解的算法.通过学习这些案例,体会算法的特点,初步感受算法思想,体会算法的基本逻辑结构,提升逻辑思维能力。
