余角和补角(1)
图片预览





文档简介
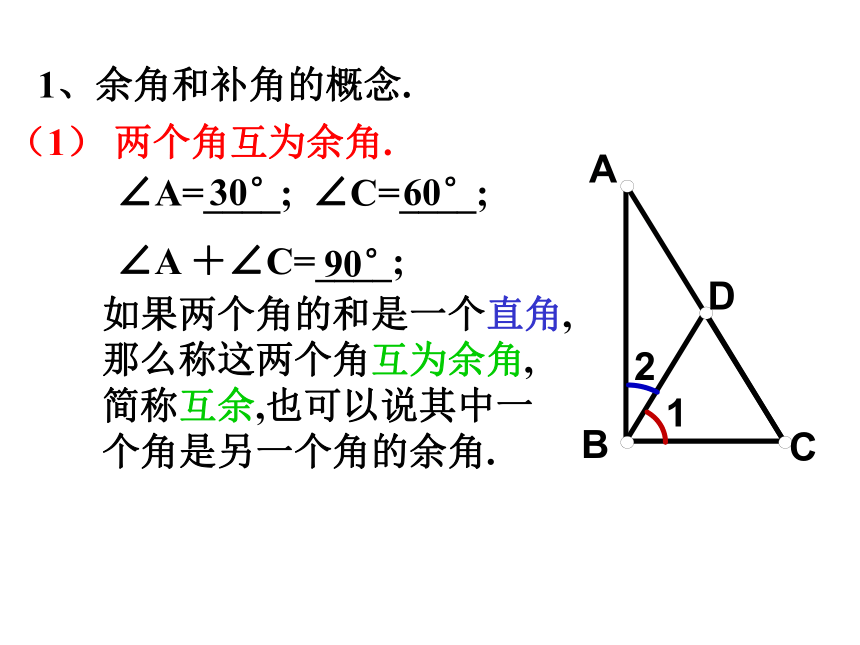
课件20张PPT。余角和补角1、余角和补角的概念.(1) 两个角互为余角.∠A=____; ∠C=____;
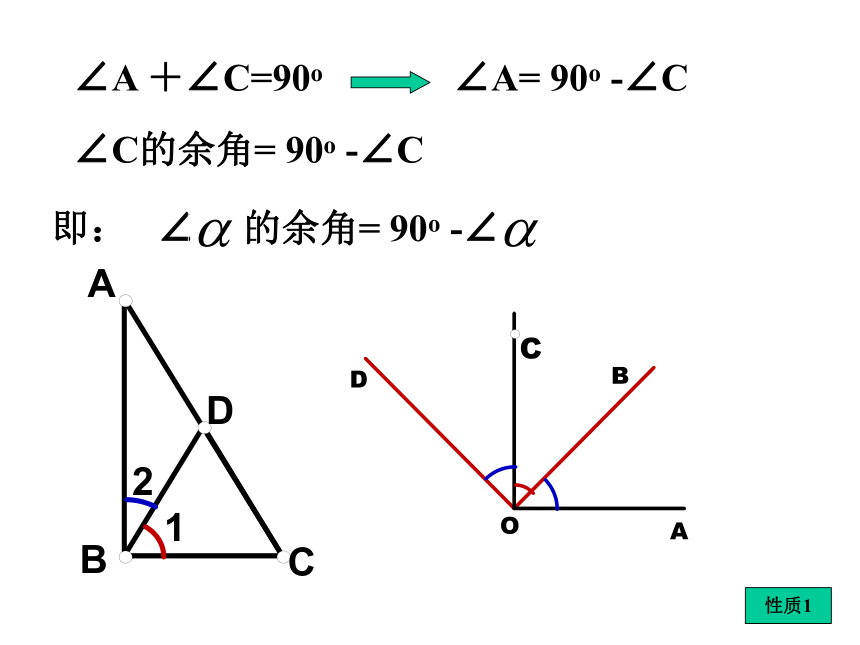
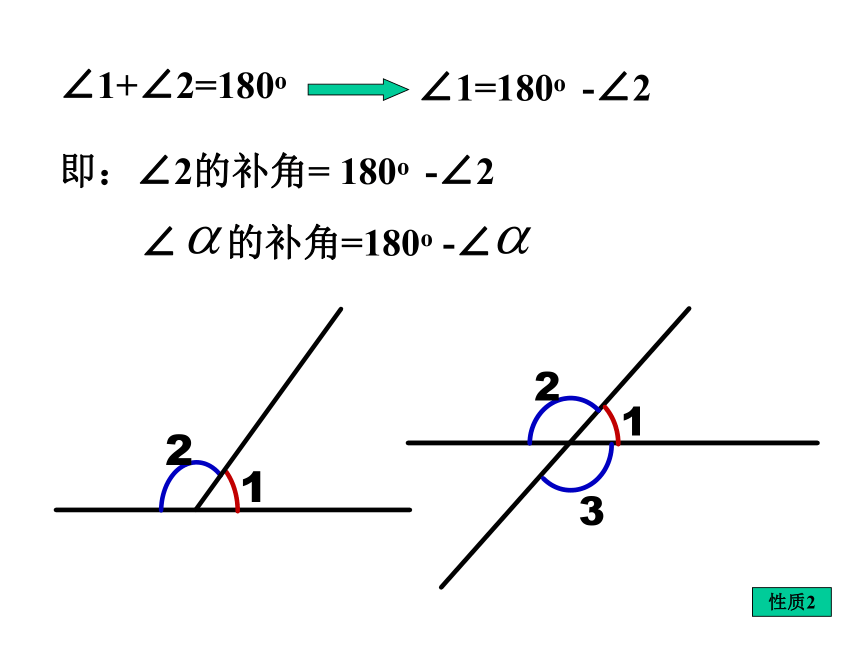
∠A +∠C=____;如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角.30°60°90°∠A +∠C=90o∠A= 90o -∠C∠C的余角= 90o -∠C性质1∠1+∠2=180o∠1=180o -∠2即:∠2的补角= 180o -∠2性质2答:这个角的余角为27°28′,补角117°28′。 2、余角和补角的性质。
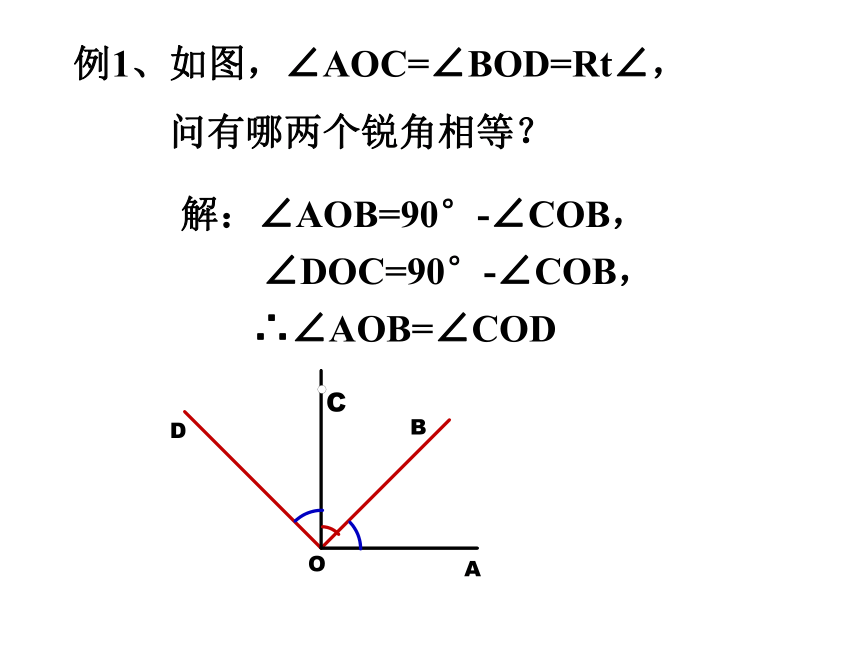
(1)余角的基本性质:同角或等角的余角相等。图形一(2)补角的基本性质:同角或等角的补角相等。图形2例1、如图,∠AOC=∠BOD=Rt∠,
问有哪两个锐角相等?解:∠AOB=90°-∠COB, ∠DOC=90°-∠COB,∴∠AOB=∠COD例2、已知一个角的补角是这个角的余角的4倍,求这个角的度数。解:设这个角为x度,则其余角为(90-x)度,补角为(180-x)度。由题意,得: 180 - x =4(90 - x)解方程,得: x =60(度)答:这个角是60°. (2)如果∠1的补角是∠1的3倍,求∠1的度数。由题意,得: 90-x=2 x-3x=-90
x=30(度)(2)如果∠1的补角是∠1的3倍,求∠1的度数。解:设∠1的度数为x度, ∠1的补角(180-x)度。由题意得: 180-x=3x -4x=-180
x=45(度)答:∠1为45°.3、综合和巩固。解:∠BOC=∠AOB -∠AOC
=90°- ∠AOC∠AOD= ∠AOB -∠BOD
=90°- ∠AOC例4、如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?_________.∠2,∠4∠3,∠1∠BOD总结:1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。练习3、如图,A、O、B三点在同一条直线上,
∠AOB=∠COD,问其中哪几对角互为补角? 解: ∠AOB=180°- ∠BOD∴ ∠AOB与∠BOD互补;∠COD=180 °- ∠AOC∴ ∠COD与∠AOC互补;又∠AOB=∠COD= 180 °- ∠AOC∴ ∠AOB与∠AOC互补;又∠COD=∠AOB= 180 °- ∠BOD∴ ∠COD与∠BOD互补;小结:
(1)余角和补角的概念,及其基本性质。(2)能运用推理或方程思想来求一个角
的余角和补角。例5、OE平分∠AOC,OD平分∠COB,则∠EOD=_____,又∠2的余角为_______,
∠2的补角为_________.课件20张PPT。余角和补角1、余角和补角的概念.(1) 两个角互为余角.∠A=____; ∠C=____;
∠A +∠C=____;如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角.30°60°90°∠A +∠C=90o∠A= 90o -∠C∠C的余角= 90o -∠C即: ∠ 的余角= 90o -∠性质1∠1+∠2=180o∠1=180o -∠2即:∠2的补角= 180o -∠2 ∠ 的补角=180o -∠性质2∠ 的余角=90°-62°32′
=27°28′练习1、已知∠ =62°32′,∠ 的余角是多少度? ∠ 的 补角是多少度?解:∠ 的余角=90°- ∠ ∠ 的补角=180o -∠ ∠ 的补角=180o - 62°32′
=117°28′答:这个角的余角为27°28′,补角117°28′。∠ 的余角=90°- ∠ ∠ 的余角=90°- ∠若∠ = ∠ 则90°- ∠ =90°- ∠即∠ 的余角= ∠ 的余角 2、余角和补角的性质。
(1)余角的基本性质:同角或等角的余角相等。图形一(2)补角的基本性质:∠ 的补角= 180o -∠∠ 的补角= 180o -∠若∠ =∠即∠ 的补角= ∠ 的补角同角或等角的补角相等。图形2例1、如图,∠AOC=∠BOD=Rt∠,
问有哪两个锐角相等?解:∠AOB=90°-∠COB, ∠DOC=90°-∠COB,∴∠AOB=∠COD例2、已知一个角的补角是这个角的余角的4倍,求这个角的度数。解:设这个角为x度,则其余角为(90-x)度,补角为(180-x)度。由题意,得: 180 - x =4(90 - x)解方程,得: x =60(度)答:这个角是60°.练习2、(1)如果∠ 的余角是∠ 的2 倍,求 ∠ 的度数。 (2)如果∠1的补角是∠1的3倍,求∠1的度数。练习2、(1)如果∠ 的余角是∠ 的2 倍,求 ∠ 的度数。解:设∠ 的度数为x度,则 ∠ 的余角为(90-x)度。由题意,得: 90-x=2 x-3x=-90
x=30(度)答:∠ 的度数为30度。(2)如果∠1的补角是∠1的3倍,求∠1的度数。解:设∠1的度数为x度, ∠1的补角(180-x)度。由题意得: 180-x=3x -4x=-180
x=45(度)答:∠1为45°.3、综合和巩固。解:∠BOC=∠AOB -∠AOC
=90°- ∠AOC∠AOD= ∠AOB -∠BOD
=90°- ∠AOC例4、如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?_________.∠2,∠4∠3,∠1∠BOD总结:1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。练习3、如图,A、O、B三点在同一条直线上,
∠AOB=∠COD,问其中哪几对角互为补角? 解: ∠AOB=180°- ∠BOD∴ ∠AOB与∠BOD互补;∠COD=180 °- ∠AOC∴ ∠COD与∠AOC互补;又∠AOB=∠COD= 180 °- ∠AOC∴ ∠AOB与∠AOC互补;又∠COD=∠AOB= 180 °- ∠BOD∴ ∠COD与∠BOD互补;小结:
(1)余角和补角的概念,及其基本性质。(2)能运用推理或方程思想来求一个角
的余角和补角。例5、OE平分∠AOC,OD平分∠COB,则∠EOD=_____,又∠2的余角为_______,
∠2的补角为_________.例6、如果∠1>∠2,那么∠2与 ( ∠1- ∠2)
之间的关系是 ( )
A、互补 B、互余
C、和为45° D、和为225°
∠A +∠C=____;如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角.30°60°90°∠A +∠C=90o∠A= 90o -∠C∠C的余角= 90o -∠C性质1∠1+∠2=180o∠1=180o -∠2即:∠2的补角= 180o -∠2性质2答:这个角的余角为27°28′,补角117°28′。 2、余角和补角的性质。
(1)余角的基本性质:同角或等角的余角相等。图形一(2)补角的基本性质:同角或等角的补角相等。图形2例1、如图,∠AOC=∠BOD=Rt∠,
问有哪两个锐角相等?解:∠AOB=90°-∠COB, ∠DOC=90°-∠COB,∴∠AOB=∠COD例2、已知一个角的补角是这个角的余角的4倍,求这个角的度数。解:设这个角为x度,则其余角为(90-x)度,补角为(180-x)度。由题意,得: 180 - x =4(90 - x)解方程,得: x =60(度)答:这个角是60°. (2)如果∠1的补角是∠1的3倍,求∠1的度数。由题意,得: 90-x=2 x-3x=-90
x=30(度)(2)如果∠1的补角是∠1的3倍,求∠1的度数。解:设∠1的度数为x度, ∠1的补角(180-x)度。由题意得: 180-x=3x -4x=-180
x=45(度)答:∠1为45°.3、综合和巩固。解:∠BOC=∠AOB -∠AOC
=90°- ∠AOC∠AOD= ∠AOB -∠BOD
=90°- ∠AOC例4、如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?_________.∠2,∠4∠3,∠1∠BOD总结:1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。练习3、如图,A、O、B三点在同一条直线上,
∠AOB=∠COD,问其中哪几对角互为补角? 解: ∠AOB=180°- ∠BOD∴ ∠AOB与∠BOD互补;∠COD=180 °- ∠AOC∴ ∠COD与∠AOC互补;又∠AOB=∠COD= 180 °- ∠AOC∴ ∠AOB与∠AOC互补;又∠COD=∠AOB= 180 °- ∠BOD∴ ∠COD与∠BOD互补;小结:
(1)余角和补角的概念,及其基本性质。(2)能运用推理或方程思想来求一个角
的余角和补角。例5、OE平分∠AOC,OD平分∠COB,则∠EOD=_____,又∠2的余角为_______,
∠2的补角为_________.课件20张PPT。余角和补角1、余角和补角的概念.(1) 两个角互为余角.∠A=____; ∠C=____;
∠A +∠C=____;如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角.30°60°90°∠A +∠C=90o∠A= 90o -∠C∠C的余角= 90o -∠C即: ∠ 的余角= 90o -∠性质1∠1+∠2=180o∠1=180o -∠2即:∠2的补角= 180o -∠2 ∠ 的补角=180o -∠性质2∠ 的余角=90°-62°32′
=27°28′练习1、已知∠ =62°32′,∠ 的余角是多少度? ∠ 的 补角是多少度?解:∠ 的余角=90°- ∠ ∠ 的补角=180o -∠ ∠ 的补角=180o - 62°32′
=117°28′答:这个角的余角为27°28′,补角117°28′。∠ 的余角=90°- ∠ ∠ 的余角=90°- ∠若∠ = ∠ 则90°- ∠ =90°- ∠即∠ 的余角= ∠ 的余角 2、余角和补角的性质。
(1)余角的基本性质:同角或等角的余角相等。图形一(2)补角的基本性质:∠ 的补角= 180o -∠∠ 的补角= 180o -∠若∠ =∠即∠ 的补角= ∠ 的补角同角或等角的补角相等。图形2例1、如图,∠AOC=∠BOD=Rt∠,
问有哪两个锐角相等?解:∠AOB=90°-∠COB, ∠DOC=90°-∠COB,∴∠AOB=∠COD例2、已知一个角的补角是这个角的余角的4倍,求这个角的度数。解:设这个角为x度,则其余角为(90-x)度,补角为(180-x)度。由题意,得: 180 - x =4(90 - x)解方程,得: x =60(度)答:这个角是60°.练习2、(1)如果∠ 的余角是∠ 的2 倍,求 ∠ 的度数。 (2)如果∠1的补角是∠1的3倍,求∠1的度数。练习2、(1)如果∠ 的余角是∠ 的2 倍,求 ∠ 的度数。解:设∠ 的度数为x度,则 ∠ 的余角为(90-x)度。由题意,得: 90-x=2 x-3x=-90
x=30(度)答:∠ 的度数为30度。(2)如果∠1的补角是∠1的3倍,求∠1的度数。解:设∠1的度数为x度, ∠1的补角(180-x)度。由题意得: 180-x=3x -4x=-180
x=45(度)答:∠1为45°.3、综合和巩固。解:∠BOC=∠AOB -∠AOC
=90°- ∠AOC∠AOD= ∠AOB -∠BOD
=90°- ∠AOC例4、如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?_________.∠2,∠4∠3,∠1∠BOD总结:1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。练习3、如图,A、O、B三点在同一条直线上,
∠AOB=∠COD,问其中哪几对角互为补角? 解: ∠AOB=180°- ∠BOD∴ ∠AOB与∠BOD互补;∠COD=180 °- ∠AOC∴ ∠COD与∠AOC互补;又∠AOB=∠COD= 180 °- ∠AOC∴ ∠AOB与∠AOC互补;又∠COD=∠AOB= 180 °- ∠BOD∴ ∠COD与∠BOD互补;小结:
(1)余角和补角的概念,及其基本性质。(2)能运用推理或方程思想来求一个角
的余角和补角。例5、OE平分∠AOC,OD平分∠COB,则∠EOD=_____,又∠2的余角为_______,
∠2的补角为_________.例6、如果∠1>∠2,那么∠2与 ( ∠1- ∠2)
之间的关系是 ( )
A、互补 B、互余
C、和为45° D、和为225°
