2.4正态分布 课件(人教B版选修2-3)
文档属性
| 名称 | 2.4正态分布 课件(人教B版选修2-3) |

|
|
| 格式 | zip | ||
| 文件大小 | 441.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-18 14:33:55 | ||
图片预览








文档简介
课件25张PPT。 1.正态曲线
态变量概率密度曲线的函数表达式为f(x)=e
,x∈R,其中参数μ为正态分布变量的
,μ∈( );σ为正态分布变量的
,σ∈ .正态变量的概率密度函数(即f(x))
的 叫做正态曲线.
期望为μ,标准差为σ的正态分布通常记作 ,
μ=0,σ=1的正态分布叫 .数学期望-∞, +∞标准差(0,+∞)图象N(μ,σ2)标准正态分布 2.正态曲线的性质
(1)曲线在x轴的 ,并且关于直线 对称;
(2)曲线在 时处于最高点,并由此处向左右两边
延伸时,曲线逐渐 ,呈现“ ”的形状;
(3)曲线的形状由参数σ确定,σ越 ,曲线“矮胖”;σ越 ,曲线越“高瘦”.上方x=μx=μ降低中间高,两边低大小 3.正态分布的3σ原则
P(μ-σ<X<μ+σ)=68.3%;
P(μ-2σ<X<μ+2σ)= ;
P(μ-3σ<X<μ+2σ)= .
正态变量的取值几乎都在距x=μ三倍标准差之内,这就是正态分布的3σ原则.95.4%99.7% 1.正态分布密度函数及正态曲线完全由变量μ和σ确定.参数μ是反映随机变量取值的平均水平的特征数,可以用样本的均值去估计;σ是衡量随机变量总体波动大小的特征数,可以用样本的标准差去估计.
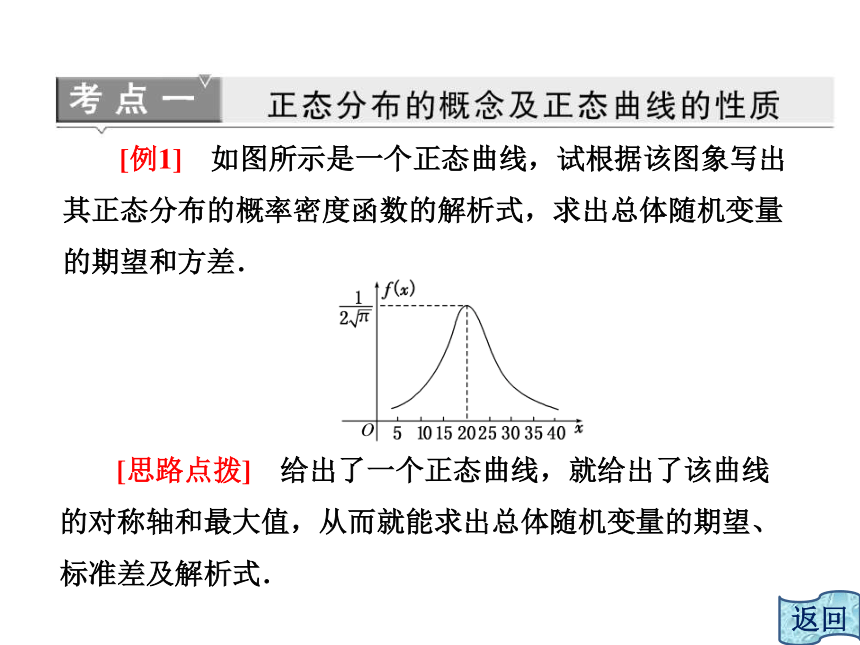
2.对于正态曲线的性质,应结合正态曲线的特点去理解、记忆. [例1] 如图所示是一个正态曲线,试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差. [思路点拨] 给出了一个正态曲线,就给出了该曲线的对称轴和最大值,从而就能求出总体随机变量的期望、标准差及解析式. [一点通] 利用正态曲线的性质可以求参数μ,σ,具体方法如下:
(1)正态曲线是单峰的,它关于直线x=μ对称,由此性质结合图象求μ.
(2)正态曲线在x=μ处达到峰值,由此性质结合图象可求σ.答案:B解析:由σ的意义可知,图象越瘦高,数据越集中,σ2越小,故有σ1>σ2>σ3.
答案:A [例2] 在某项测量中,测量结果服从正态分布N(1,4),求正态总体X在(-1,1)内取值的概率.
[思路点拨] 解答本题可先求出X在(-1,3)内取值的概率,然后由正态曲线关于x=1对称知,X在(-1,1)内取值的概率就等于在(-1,3)内取值的概率的一半. [一点通] 解答此类问题的关键在于充分利用正态曲线的对称性,把待求区间内的概率向已知区间内的概率进行转化,在此过程中注意数形结合思想的运用.3.若随机变量X~N(μ,σ2),则P(X≤μ)=________.4.设随机变量X服从正态分布N(2,9),若P(X>c+1)=
P(X [例3] (10分)据调查统计,某市高二学生中男生的身高X(单位:cm)服从正态分布N(174,9).若该市共有高二男生3 000人,试估计该市高二男生身高在(174,180)范围内的人数.
[思路点拨] 因为μ=174,σ=3,所以可利用正态分布的性质可以求解.[精解详析] 因为身高X~N(174,9),
所以μ=174,σ=3, (2分)
所以μ-2σ=174-2×3=168,
μ+2σ=174+2×3=180,
所以身高在(168,180]范围内的概率为0.954 4. (6分)
又因为μ=174.
所以身高在(168,174)和(174,180)范围内的概率相等,均为0.477 2,
故该市高二男生身高在(174,180)范围内的人数是
3 000×0.477 2≈1 432(人). (10分) [一点通] 解决此类问题一定要灵活把握3σ原则,将所求概率向P(μ-σ交通拥挤,所需时间(单位:分)服从X~N(50,102),则他在时间段(30,70)内赶到火车站的概率为______.
解析:∵X~N(50,102),∴μ=50,σ=10.
∴P(30答案:0.954 47.灯泡厂生产的白炽灯泡的寿命为X(单位:小时),已
知X~N(1 000,302),要使灯泡的平均寿命为1000小时的概率约为99.7%,则灯泡的最低寿命应控制在多少小时以上?
解:因为灯泡的使用寿命X~N(1 000,302),
故X在(1 000-3×30,1 000+3×30)的概率为99.7%,
即X在(910,1 090)内取值的概率约为99.7%,
故灯泡的最低使用寿命应控制在910小时以上. 因为P(μ-3σ<X<μ+3σ)=0.997 4,所以正态总体X几乎总取值于区间(μ-3σ,μ+3σ)之内,而在此区间以外取值的概率只有0.0026,这是一个小概率事件,通常认为这种情况在一次试验中几乎不可能发生.这是统计中常用的假设检验基本思想.
态变量概率密度曲线的函数表达式为f(x)=e
,x∈R,其中参数μ为正态分布变量的
,μ∈( );σ为正态分布变量的
,σ∈ .正态变量的概率密度函数(即f(x))
的 叫做正态曲线.
期望为μ,标准差为σ的正态分布通常记作 ,
μ=0,σ=1的正态分布叫 .数学期望-∞, +∞标准差(0,+∞)图象N(μ,σ2)标准正态分布 2.正态曲线的性质
(1)曲线在x轴的 ,并且关于直线 对称;
(2)曲线在 时处于最高点,并由此处向左右两边
延伸时,曲线逐渐 ,呈现“ ”的形状;
(3)曲线的形状由参数σ确定,σ越 ,曲线“矮胖”;σ越 ,曲线越“高瘦”.上方x=μx=μ降低中间高,两边低大小 3.正态分布的3σ原则
P(μ-σ<X<μ+σ)=68.3%;
P(μ-2σ<X<μ+2σ)= ;
P(μ-3σ<X<μ+2σ)= .
正态变量的取值几乎都在距x=μ三倍标准差之内,这就是正态分布的3σ原则.95.4%99.7% 1.正态分布密度函数及正态曲线完全由变量μ和σ确定.参数μ是反映随机变量取值的平均水平的特征数,可以用样本的均值去估计;σ是衡量随机变量总体波动大小的特征数,可以用样本的标准差去估计.
2.对于正态曲线的性质,应结合正态曲线的特点去理解、记忆. [例1] 如图所示是一个正态曲线,试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差. [思路点拨] 给出了一个正态曲线,就给出了该曲线的对称轴和最大值,从而就能求出总体随机变量的期望、标准差及解析式. [一点通] 利用正态曲线的性质可以求参数μ,σ,具体方法如下:
(1)正态曲线是单峰的,它关于直线x=μ对称,由此性质结合图象求μ.
(2)正态曲线在x=μ处达到峰值,由此性质结合图象可求σ.答案:B解析:由σ的意义可知,图象越瘦高,数据越集中,σ2越小,故有σ1>σ2>σ3.
答案:A [例2] 在某项测量中,测量结果服从正态分布N(1,4),求正态总体X在(-1,1)内取值的概率.
[思路点拨] 解答本题可先求出X在(-1,3)内取值的概率,然后由正态曲线关于x=1对称知,X在(-1,1)内取值的概率就等于在(-1,3)内取值的概率的一半. [一点通] 解答此类问题的关键在于充分利用正态曲线的对称性,把待求区间内的概率向已知区间内的概率进行转化,在此过程中注意数形结合思想的运用.3.若随机变量X~N(μ,σ2),则P(X≤μ)=________.4.设随机变量X服从正态分布N(2,9),若P(X>c+1)=
P(X
[思路点拨] 因为μ=174,σ=3,所以可利用正态分布的性质可以求解.[精解详析] 因为身高X~N(174,9),
所以μ=174,σ=3, (2分)
所以μ-2σ=174-2×3=168,
μ+2σ=174+2×3=180,
所以身高在(168,180]范围内的概率为0.954 4. (6分)
又因为μ=174.
所以身高在(168,174)和(174,180)范围内的概率相等,均为0.477 2,
故该市高二男生身高在(174,180)范围内的人数是
3 000×0.477 2≈1 432(人). (10分) [一点通] 解决此类问题一定要灵活把握3σ原则,将所求概率向P(μ-σ
解析:∵X~N(50,102),∴μ=50,σ=10.
∴P(30
知X~N(1 000,302),要使灯泡的平均寿命为1000小时的概率约为99.7%,则灯泡的最低寿命应控制在多少小时以上?
解:因为灯泡的使用寿命X~N(1 000,302),
故X在(1 000-3×30,1 000+3×30)的概率为99.7%,
即X在(910,1 090)内取值的概率约为99.7%,
故灯泡的最低使用寿命应控制在910小时以上. 因为P(μ-3σ<X<μ+3σ)=0.997 4,所以正态总体X几乎总取值于区间(μ-3σ,μ+3σ)之内,而在此区间以外取值的概率只有0.0026,这是一个小概率事件,通常认为这种情况在一次试验中几乎不可能发生.这是统计中常用的假设检验基本思想.
