苏科版八年级数学下册 9.3 平行四边形 教案 (表格式)
文档属性
| 名称 | 苏科版八年级数学下册 9.3 平行四边形 教案 (表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 80.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 08:00:38 | ||
图片预览

文档简介
课 题 9.3 平行四边形(2) 教学模式
教学目标(认知技能情感) 1.在数学学习活动中获得成功的体验,锻炼克服困难的意志,建立自信心。 2.体验数学活动充满着探索与创造,感受数学的严谨性以及数学结论的确定性,并培 养实事求是的态度。 3用类比、逆向思维的方式探索平行四边形的判定方法。通过猜想,推理,最终发现并得出判定方法。 4.掌握平行四边形的判别方法,会利用平行四边形的性质和判别进行有关线段的证明和角的计算。 5.通过本节的学习,进一步发展学生的推理能力,提高学生的逻辑思维能力。
教学重难点 平行四边形条件的过程的探索及应用. 平行四边形条件的探索
教学环节 学生自学共研的内容方法 (按环节设计自学、讨论、训练、探索、创新等内容) 教师施教提要 (启发、精讲、活动等) 再次 优化
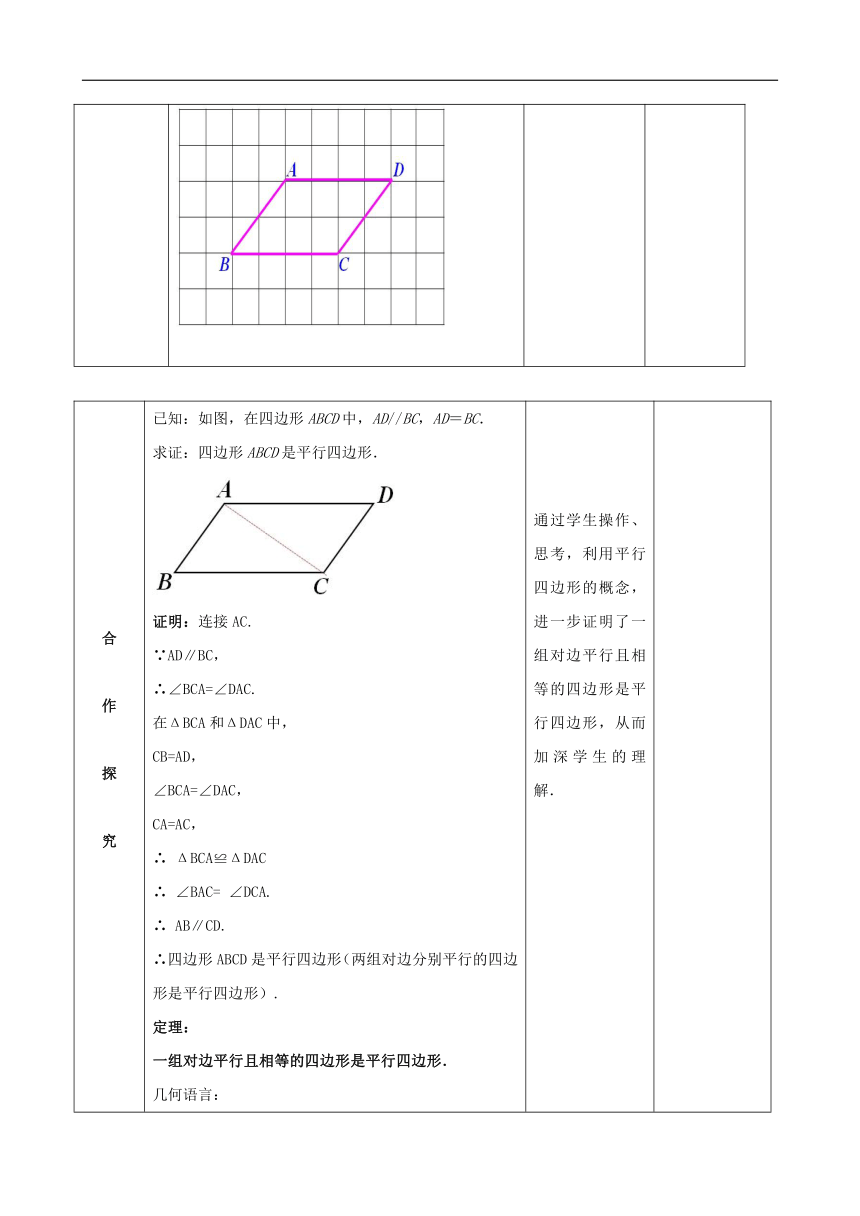
导 入 合 作 探 究 复习引入 如图,在下列各题中,再添上一个条件使结论成立: (1)∵ AB∥CD, , ∴ 四边形ABCD是平行四边形. (2)∵ AB=CD, , (
D
C
A
B
) ∴ 四边形ABCD是平行四边形. 如果只考虑一组对边,它们满足什么条件时,这个四边形能成为平行四边形? 问题情境 (1)回忆平行四边形的概念; (2)在方格纸上画两条互相平行并且相等的线段AD、BC,连接AB、DC. 你能证明所画四边形ABCD是平行四边形吗? 利用网格画图,学生能够容易得出结论.
合 作 探 究 已知:如图,在四边形ABCD中,AD//BC,AD=BC. 求证:四边形ABCD是平行四边形. 证明:连接AC. ∵AD∥BC, ∴∠BCA=∠DAC. 在ΔBCA和ΔDAC中, CB=AD, ∠BCA=∠DAC, CA=AC, ∴ ΔBCA≌ΔDAC ∴ ∠BAC= ∠DCA. ∴ AB∥CD. ∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形). 定理: 一组对边平行且相等的四边形是平行四边形. 几何语言: ∵AD//BC,AD=BC, ∴四边形ABCD是平行四边形. 探索活动 在四边形ABCD中,AB=CD,AD=BC.四边形ABCD是平行四边形吗?证明你的结论. 证明:连结AC 在△ABC和△CDA中 AB=CD(已知) AD=CB (已知) AC=CA (公共边) ∴△ABC≌△CDA(SSS) ∴∠1=∠2,∠3=∠4(全等三角形的对应角相等) ∴ AB∥CD,AD∥BC (内错角相等,两直线平行) ∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形) 定理: 两组对边分别相等的四边形是平行四边形. 几何语言: ∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形. 通过学生操作、思考,利用平行四边形的概念,进一步证明了一组对边平行且相等的四边形是平行四边形,从而加深学生的理解. 使学生能够运用平行四边形的概念和定理证明四边形是平行四边形,从而得到两组对边分别相等的四边形是平行四边形.
随堂 练习 课堂 小结 达标 检测 新知应用 已知:如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF. 求证:四边形BFDE是平行四边形. (
E
F
B
A
D
C
) 证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC(平行四边形的对边平行且相等). ∵AE=CF, ∴AD-AE=BC-CF, 即 DE=BF. ∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形). ] 拓展延伸 如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形. 如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF,AE、BE相交于点G,CE、DF相交于点H. 求证:EF与GH互相平分。 培养学生运用几何语言进行说理的规范性. 通过练习设置,使学生在运用新知识的过程中能够进行有条理的思考并进行简单的推理.
布置 作业 课堂作业 讲义 课后作业 讲义
教后感 平行四边形的判定学生比较容易理解,关键是在应用以及过程书写上存在问题,需要多加练习。
教学目标(认知技能情感) 1.在数学学习活动中获得成功的体验,锻炼克服困难的意志,建立自信心。 2.体验数学活动充满着探索与创造,感受数学的严谨性以及数学结论的确定性,并培 养实事求是的态度。 3用类比、逆向思维的方式探索平行四边形的判定方法。通过猜想,推理,最终发现并得出判定方法。 4.掌握平行四边形的判别方法,会利用平行四边形的性质和判别进行有关线段的证明和角的计算。 5.通过本节的学习,进一步发展学生的推理能力,提高学生的逻辑思维能力。
教学重难点 平行四边形条件的过程的探索及应用. 平行四边形条件的探索
教学环节 学生自学共研的内容方法 (按环节设计自学、讨论、训练、探索、创新等内容) 教师施教提要 (启发、精讲、活动等) 再次 优化
导 入 合 作 探 究 复习引入 如图,在下列各题中,再添上一个条件使结论成立: (1)∵ AB∥CD, , ∴ 四边形ABCD是平行四边形. (2)∵ AB=CD, , (
D
C
A
B
) ∴ 四边形ABCD是平行四边形. 如果只考虑一组对边,它们满足什么条件时,这个四边形能成为平行四边形? 问题情境 (1)回忆平行四边形的概念; (2)在方格纸上画两条互相平行并且相等的线段AD、BC,连接AB、DC. 你能证明所画四边形ABCD是平行四边形吗? 利用网格画图,学生能够容易得出结论.
合 作 探 究 已知:如图,在四边形ABCD中,AD//BC,AD=BC. 求证:四边形ABCD是平行四边形. 证明:连接AC. ∵AD∥BC, ∴∠BCA=∠DAC. 在ΔBCA和ΔDAC中, CB=AD, ∠BCA=∠DAC, CA=AC, ∴ ΔBCA≌ΔDAC ∴ ∠BAC= ∠DCA. ∴ AB∥CD. ∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形). 定理: 一组对边平行且相等的四边形是平行四边形. 几何语言: ∵AD//BC,AD=BC, ∴四边形ABCD是平行四边形. 探索活动 在四边形ABCD中,AB=CD,AD=BC.四边形ABCD是平行四边形吗?证明你的结论. 证明:连结AC 在△ABC和△CDA中 AB=CD(已知) AD=CB (已知) AC=CA (公共边) ∴△ABC≌△CDA(SSS) ∴∠1=∠2,∠3=∠4(全等三角形的对应角相等) ∴ AB∥CD,AD∥BC (内错角相等,两直线平行) ∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形) 定理: 两组对边分别相等的四边形是平行四边形. 几何语言: ∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形. 通过学生操作、思考,利用平行四边形的概念,进一步证明了一组对边平行且相等的四边形是平行四边形,从而加深学生的理解. 使学生能够运用平行四边形的概念和定理证明四边形是平行四边形,从而得到两组对边分别相等的四边形是平行四边形.
随堂 练习 课堂 小结 达标 检测 新知应用 已知:如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF. 求证:四边形BFDE是平行四边形. (
E
F
B
A
D
C
) 证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC(平行四边形的对边平行且相等). ∵AE=CF, ∴AD-AE=BC-CF, 即 DE=BF. ∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形). ] 拓展延伸 如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形. 如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF,AE、BE相交于点G,CE、DF相交于点H. 求证:EF与GH互相平分。 培养学生运用几何语言进行说理的规范性. 通过练习设置,使学生在运用新知识的过程中能够进行有条理的思考并进行简单的推理.
布置 作业 课堂作业 讲义 课后作业 讲义
教后感 平行四边形的判定学生比较容易理解,关键是在应用以及过程书写上存在问题,需要多加练习。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
