9.3用正多边形铺设地面练习2021-2022学年华东师大版数学七年级下册 (word版含答案)
文档属性
| 名称 | 9.3用正多边形铺设地面练习2021-2022学年华东师大版数学七年级下册 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 177.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 08:08:34 | ||
图片预览




文档简介
9.3用正多边形铺设地面
★用一些不重叠放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面(或平面镶嵌).
★关于正多边形的镶嵌有三个条件限制
边长相等;(2)顶点公共;(8)在一个顶点处各正多边形的内角之和为360度.
★正多边形铺设:根据多边形内角和公式( n 一2).180,计算出正多边形的每一个内角的度数,如果它的整数倍是360,那么该正多边形就能铺满地否则就不能
★用多种正多边形能否铺满地面,一要看顶点处所取正多边形的几个内角的和是否恰好为一个周角;二要看这几种正多边形的边长是否相等。
一.选择题(共10小题)
1.下列图形中能够用来作平面镶嵌的是( )
A.正八边形 B.正七边形 C.正六边形 D.正五边形
2.只用下列哪一种正多边形可以进行平面镶嵌( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
3.若铺满地面的瓷砖每一个顶点处由6块相同的正多边形组成,此时的正多边形只能是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
4.某家庭装修新房,下列组合不能够无缝隙不重叠铺设美丽地板的是( )
A.正三角形和正六边形
B.正五边形和正十边形
C.正方形和正八边形
D.正三角形、正六边形和正方形
5.用边长相等的下列两种正多边形,不能进行平面镶嵌的是( )
A.等边三角形和正六边形 B.正方形和正八边形
C.正五边形和正十边形 D.正六边形和正十二边形
6.利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0),则a+b的值为( )
A.3或4 B.4或5 C.5或6 D.4
7.用两种正多边形组合铺满地面,其中的一种是正八边形,则另一种是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
8.用两种正多边形镶嵌,不能与正三角形匹配的正多边形是( )
A.正方形 B.正六边形 C.正十二边形 D.正十八边形
9.下列组合不能密铺平面的是( )
A.正三角形、正方形和正六边形
B.正三角形、正方形和正十二边形
C.正三角形、正六边形和正十二边形
D.正方形、正六边形和正十二边形
10.下列每组图形,不能镶嵌整个平面的是( )
A. B.
C. D.
二.填空题(共7小题)
11.在下面的多边形中:①正三角形;②正方形;③正五边形;④正六边形,如果只用一种正多边形进行镶嵌,那么不能镶嵌成一个平面的有 (只填序号)
12.用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y= .
13.如图,用三个完全相同的正五边形地砖平铺地面,则空余的角度是 度.
14.王老师家准备用边长相等的正四边形和正八边形的地面砖铺客厅,铺设图案如图所示.购买这两种正多边形地砖的数量之比约为 .
15.用三块正多边形的木板铺地,拼在一起并相交于一点的各边完全吻合,若其中两块木板的边数均为5,则第三块木板的边数为 .
16.我们知道形状为正五边形的地砖不能铺满地面,但某公园的一段路面是用型号相同的特殊的五边形地砖铺成的.如图,是拼铺图案的一部分,其中每个五边形有3个内角相等,那么这3个内角都等于 度.
17.如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖密铺,从里向外共铺了10层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第10层的外边界所围成的多边形的周长是 m.
三.解答题(共3小题)
18.正三角形,正四边形可以铺满地面,但正十二边形和正八边形均不能铺满地面.试问,
(1)正三角形和正十二边形的结合能否铺满地面?如果可以,举例说明;如果不行,说明理由.
(2)由正四边形和正八变形组合呢?
19.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫作平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
正多边形的边数 3 4 5 6 8
正多边形每个内角的度数 60° 90°
(1)填写表中空格.
(2)根据题意,如果仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)假设在镶嵌的平面图形的一个顶点周围有m个正四边形、n个正八边形,求m和n的值,请写出过程.
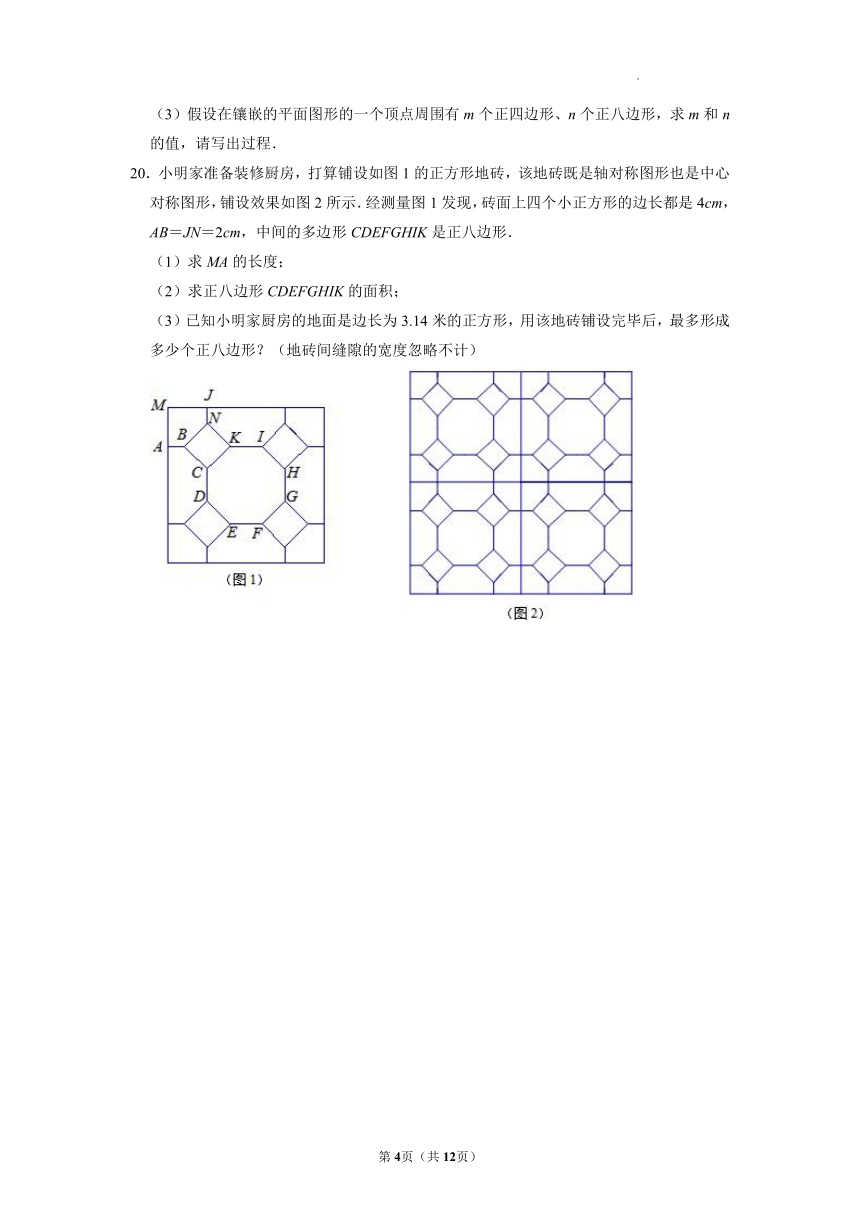
20.小明家准备装修厨房,打算铺设如图1的正方形地砖,该地砖既是轴对称图形也是中心对称图形,铺设效果如图2所示.经测量图1发现,砖面上四个小正方形的边长都是4cm,AB=JN=2cm,中间的多边形CDEFGHIK是正八边形.
(1)求MA的长度;
(2)求正八边形CDEFGHIK的面积;
(3)已知小明家厨房的地面是边长为3.14米的正方形,用该地砖铺设完毕后,最多形成多少个正八边形?(地砖间缝隙的宽度忽略不计)
9.3用正多边形铺设地面
参考答案与试题解析
一.选择题(共10小题)
1.下列图形中能够用来作平面镶嵌的是( )
A.正八边形 B.正七边形 C.正六边形 D.正五边形
【解答】解:A、正八边形的每个内角为:180°﹣360°÷8=135°,不能整除360°,不能密铺;
B、正七边形每个内角为:180°﹣360°÷7=900÷7,不能整除360°,不能密铺;
C、正六边形的每个内角是120°,能整除360°,能密铺;
D、正五边形的每个内角是108°,不能整除360°,不能密铺.
故选:C.
2.只用下列哪一种正多边形可以进行平面镶嵌( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
【解答】解:A、正五边形的每个内角度数为180°﹣360°÷5=108°,不能整除360°,不能进行平面镶嵌,不符合题意;
B、正六边形的每个内角度数为180°﹣360°÷6=120°,能整除360°,能进行平面镶嵌,符合题意;
C、正八边形的每个内角度数为180°﹣360°÷8=135°,不能整除360°,不能进行平面镶嵌,不符合题意;
D、正十边形的每个内角度数为180°﹣360°÷10=144°,不能整除360°,不能进行平面镶嵌,不符合题意;
故选:B.
3.若铺满地面的瓷砖每一个顶点处由6块相同的正多边形组成,此时的正多边形只能是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
【解答】解:A、6个正三角形满足同一顶点处的周角为360°,故本选项正确;
B、6个正四边形不满足同一顶点处的周角为360°,故本选项错误;
C、6个正六边形不满足同一顶点处的周角为360°,故本选项错误;
D、6个正八边形不满足同一顶点处的周角为360°,故本选项错误;
故选:A.
4.某家庭装修新房,下列组合不能够无缝隙不重叠铺设美丽地板的是( )
A.正三角形和正六边形
B.正五边形和正十边形
C.正方形和正八边形
D.正三角形、正六边形和正方形
【解答】解:∵用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.
∴为了能够做到无缝隙、不重叠地铺设,购买的地板砖形状不能是正五边形和正十边形.
故选:B.
5.用边长相等的下列两种正多边形,不能进行平面镶嵌的是( )
A.等边三角形和正六边形 B.正方形和正八边形
C.正五边形和正十边形 D.正六边形和正十二边形
【解答】解:A、正三角形的每个内角是60°,正六边形的每个内角是120°,∵2×60°+2×120°=360°,能密铺,故此选项不合题意;
B、正八边形的每个内角是135°,正方形的每个内角是90°,∵2×135°+90°=360°,能密铺,故此选项不合题意;
C、正五形的每个内角是108°,正十边形的每个内角是144°,∵2×108°+144°=360°,能密铺,故此选项不合题意;
D、正六边形的每个内角是120°和正十二边形的每个内角是150°,120m+150n=360°,m=3﹣n,显然n取任何正整数时,m不能得正整数,故不能铺满,符合题意.
故选:D.
6.利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0),则a+b的值为( )
A.3或4 B.4或5 C.5或6 D.4
【解答】解:∵正三边形和正六边形内角分别为60°、120°,
60°×4+120°=360°,或60°×2+120°×2=360°,
∴a=4,b=1或a=2,b=2,
①当a=4,b=1时,a+b=5;
②当a=2,b=2时,a+b=4.
故选:B.
7.用两种正多边形组合铺满地面,其中的一种是正八边形,则另一种是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
【解答】解:正八边形的一个内角=180°﹣=135°,
360°﹣2×135°=90°,
∵正方形的每个内角是90°,
∴另一种是正方形.
故选:B.
8.用两种正多边形镶嵌,不能与正三角形匹配的正多边形是( )
A.正方形 B.正六边形 C.正十二边形 D.正十八边形
【解答】解:A、正三角形的每个内角是60°,正方形的每个内角是90°.∵3×60°+2×90°=360°,∴正方形能匹配;
B、正六边形的每个内角是120°,正三角形的每个内角是60度.∵2×120°+2×60°=360°,或120°+4×60°=360°,∴正六边形能匹配;
C、正三角形的每个内角是60°,正十二边形的每个内角是180°﹣360°÷12=150°,∵60°+2×150°=360°,∴正十二边形能匹配;
D、正三角形的每个内角是60°,正十八边形内角为160°,显然不能构成360°的周角,故不能匹配.
故选:D.
9.下列组合不能密铺平面的是( )
A.正三角形、正方形和正六边形
B.正三角形、正方形和正十二边形
C.正三角形、正六边形和正十二边形
D.正方形、正六边形和正十二边形
【解答】解:A、正三角形、正方形和正六边形,可以密铺平面,比如:2个正方形,一个正六边形,一个正三角形.本选项不符合题意;
B、正三角形、正方形和正十二边形,可以密铺平面,比如:2个正三角形、一个正方形、一个正十二边形.本选项不符合题意;
C、正三角形、正六边形和正十二边形,不能密铺平面.本选项符合题意;
D、正方形、正六边形和正十二边形.可以密铺平面,比如:一个正方形、一个正六边形、一个正十二边形.本选项不符合题意;
故选:C.
10.下列每组图形,不能镶嵌整个平面的是( )
A. B.
C. D.
【解答】解:A、2个三角形2个正六边形或4个三角形1个正六边形可以镶嵌.本选项不符合题意.
B、1个右边的图和4个左边的图,可以镶嵌.本选项不符合题意.
C、正方形的内角为90°,矩形的内角为90°,可以镶嵌.本选项不符合题意.
D、正方形与正六边形,不可以镶嵌.本选项符合题意.
故选:D.
二.填空题(共7小题)
11.在下面的多边形中:①正三角形;②正方形;③正五边形;④正六边形,如果只用一种正多边形进行镶嵌,那么不能镶嵌成一个平面的有 ③ (只填序号)
【解答】解:①正三角形的每个内角是60°,能整除360°,能密铺;
②正方形的每个内角是90°,4个能密铺;
③正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺;
④正六边形的每个内角是120°,3个能密铺,
故不能镶嵌成一个平面的有③.
故答案为:③.
12.用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y= 11 .
【解答】解:要拼接成周长等于18的拼接图形,需要4或5或6或7个单位六边形.
故x=4,y=7,
则x+y=11.
故答案为:11.
13.如图,用三个完全相同的正五边形地砖平铺地面,则空余的角度是 36 度.
【解答】解:∵正五边形每个内角是180°﹣360°÷5=108°,
∴空余的角度=360°﹣3×108°=36°.
14.王老师家准备用边长相等的正四边形和正八边形的地面砖铺客厅,铺设图案如图所示.购买这两种正多边形地砖的数量之比约为 1:1 .
【解答】解:由铺设图案和镶嵌的条件可知购买边长相等的正四边形和正八边形这两种正多边形地砖的数量之比约为1:1.
15.用三块正多边形的木板铺地,拼在一起并相交于一点的各边完全吻合,若其中两块木板的边数均为5,则第三块木板的边数为 10 .
【解答】解:正五边形每个内角是180°﹣360°÷5=108°,顶点处已经有2个内角,度数之和为:108×2=216°,
那么另一个多边形的内角度数为:360°﹣216°=144°,
相邻的外角为:180°﹣144°=36°,
∴边数为:360°÷36°=10.
16.我们知道形状为正五边形的地砖不能铺满地面,但某公园的一段路面是用型号相同的特殊的五边形地砖铺成的.如图,是拼铺图案的一部分,其中每个五边形有3个内角相等,那么这3个内角都等于 120 度.
【解答】解:因为3个内角放在同一顶点处,组成一个周角,所以每个内角为:360°÷3=120°.
故这3个内角都等于120度.
17.如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖密铺,从里向外共铺了10层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第10层的外边界所围成的多边形的周长是 33 m.
【解答】解:根据题意分析可得:从里向外的第1层是6×2+6=18边形.
第2层是6×3+6=24边形.
此后,每层都比前一层多6条边.
依此递推,第10层是6×10+6=66边形.
∵边长为0.5m,∴第10层的外边界所围成的多边形的周长是66×0.5=33m.
故应填:33.
三.解答题(共3小题)
18.正三角形,正四边形可以铺满地面,但正十二边形和正八边形均不能铺满地面.试问,
(1)正三角形和正十二边形的结合能否铺满地面?如果可以,举例说明;如果不行,说明理由.
(2)由正四边形和正八变形组合呢?
【解答】解:(1)∵正三角形的每个内角是60°,正十二边形的每个内角是150°,
又∵60°+2×150°=360°,
∴用1个正三角形和2个正十二边形的结合能铺满地面;
(2)∵正四边形的每个内角是90°,正八边形的每个内角是135°,
又∵90°+2×135°=360°,
∴正四边形和正八边形组合能铺满地面.
19.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫作平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
正多边形的边数 3 4 5 6 8
正多边形每个内角的度数 60° 90° 108° 120° 135°
(1)填写表中空格.
(2)根据题意,如果仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)假设在镶嵌的平面图形的一个顶点周围有m个正四边形、n个正八边形,求m和n的值,请写出过程.
【解答】解:(1)正五边形每个内角的度数为:;
正六边形每个内角的度数为:;
正八边形每个内角的度数为:;
(2)因为,,,,,
所以仅用一种正多边形镶嵌,正三角形、正四边形、正六边形能镶嵌成一个平面图形;
(3)根据题意知90°m+135°n=360°,且m,n均为正整数,
即m,n是方程2m+3n=8的正整数解,
当m=1时,n=2,满足题意;
当m=2时,n=,不满足题意.
所以m=1,n=2.
20.小明家准备装修厨房,打算铺设如图1的正方形地砖,该地砖既是轴对称图形也是中心对称图形,铺设效果如图2所示.经测量图1发现,砖面上四个小正方形的边长都是4cm,AB=JN=2cm,中间的多边形CDEFGHIK是正八边形.
(1)求MA的长度;
(2)求正八边形CDEFGHIK的面积;
(3)已知小明家厨房的地面是边长为3.14米的正方形,用该地砖铺设完毕后,最多形成多少个正八边形?(地砖间缝隙的宽度忽略不计)
【解答】解:(1)连接BK和NC,两线的交点为O,
∵四边形BCKN是正方形,
∴∠NOB=90°,OB=ON,
∵BN=4cm,
∴由勾股定理得:BO=ON=2cm,
∵JN=2cm,
∴AM=JO=(2+2)cm;
(2)如图,作小正方形的对角线,组成正方形ORZQ,
则正方形的边长为(2+4+2)cm,即为(4+4)cm,
所以正八边形CDEFGHIK的面积为S正方形OQZR﹣4S△BOC=(4+4)2﹣4××2×2=(32+32)cm2;
(3)正方形地砖的边长为:2×(2+2)cm+(4+4)cm=(8+8)cm,
∵3.14米=314cm,
∴3142÷(8+8)2≈264,
∵162<264,
∴用该地砖铺设完毕后,最多形成32×32=1024个正八边形.
第1页(共1页)
★用一些不重叠放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面(或平面镶嵌).
★关于正多边形的镶嵌有三个条件限制
边长相等;(2)顶点公共;(8)在一个顶点处各正多边形的内角之和为360度.
★正多边形铺设:根据多边形内角和公式( n 一2).180,计算出正多边形的每一个内角的度数,如果它的整数倍是360,那么该正多边形就能铺满地否则就不能
★用多种正多边形能否铺满地面,一要看顶点处所取正多边形的几个内角的和是否恰好为一个周角;二要看这几种正多边形的边长是否相等。
一.选择题(共10小题)
1.下列图形中能够用来作平面镶嵌的是( )
A.正八边形 B.正七边形 C.正六边形 D.正五边形
2.只用下列哪一种正多边形可以进行平面镶嵌( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
3.若铺满地面的瓷砖每一个顶点处由6块相同的正多边形组成,此时的正多边形只能是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
4.某家庭装修新房,下列组合不能够无缝隙不重叠铺设美丽地板的是( )
A.正三角形和正六边形
B.正五边形和正十边形
C.正方形和正八边形
D.正三角形、正六边形和正方形
5.用边长相等的下列两种正多边形,不能进行平面镶嵌的是( )
A.等边三角形和正六边形 B.正方形和正八边形
C.正五边形和正十边形 D.正六边形和正十二边形
6.利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0),则a+b的值为( )
A.3或4 B.4或5 C.5或6 D.4
7.用两种正多边形组合铺满地面,其中的一种是正八边形,则另一种是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
8.用两种正多边形镶嵌,不能与正三角形匹配的正多边形是( )
A.正方形 B.正六边形 C.正十二边形 D.正十八边形
9.下列组合不能密铺平面的是( )
A.正三角形、正方形和正六边形
B.正三角形、正方形和正十二边形
C.正三角形、正六边形和正十二边形
D.正方形、正六边形和正十二边形
10.下列每组图形,不能镶嵌整个平面的是( )
A. B.
C. D.
二.填空题(共7小题)
11.在下面的多边形中:①正三角形;②正方形;③正五边形;④正六边形,如果只用一种正多边形进行镶嵌,那么不能镶嵌成一个平面的有 (只填序号)
12.用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y= .
13.如图,用三个完全相同的正五边形地砖平铺地面,则空余的角度是 度.
14.王老师家准备用边长相等的正四边形和正八边形的地面砖铺客厅,铺设图案如图所示.购买这两种正多边形地砖的数量之比约为 .
15.用三块正多边形的木板铺地,拼在一起并相交于一点的各边完全吻合,若其中两块木板的边数均为5,则第三块木板的边数为 .
16.我们知道形状为正五边形的地砖不能铺满地面,但某公园的一段路面是用型号相同的特殊的五边形地砖铺成的.如图,是拼铺图案的一部分,其中每个五边形有3个内角相等,那么这3个内角都等于 度.
17.如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖密铺,从里向外共铺了10层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第10层的外边界所围成的多边形的周长是 m.
三.解答题(共3小题)
18.正三角形,正四边形可以铺满地面,但正十二边形和正八边形均不能铺满地面.试问,
(1)正三角形和正十二边形的结合能否铺满地面?如果可以,举例说明;如果不行,说明理由.
(2)由正四边形和正八变形组合呢?
19.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫作平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
正多边形的边数 3 4 5 6 8
正多边形每个内角的度数 60° 90°
(1)填写表中空格.
(2)根据题意,如果仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)假设在镶嵌的平面图形的一个顶点周围有m个正四边形、n个正八边形,求m和n的值,请写出过程.
20.小明家准备装修厨房,打算铺设如图1的正方形地砖,该地砖既是轴对称图形也是中心对称图形,铺设效果如图2所示.经测量图1发现,砖面上四个小正方形的边长都是4cm,AB=JN=2cm,中间的多边形CDEFGHIK是正八边形.
(1)求MA的长度;
(2)求正八边形CDEFGHIK的面积;
(3)已知小明家厨房的地面是边长为3.14米的正方形,用该地砖铺设完毕后,最多形成多少个正八边形?(地砖间缝隙的宽度忽略不计)
9.3用正多边形铺设地面
参考答案与试题解析
一.选择题(共10小题)
1.下列图形中能够用来作平面镶嵌的是( )
A.正八边形 B.正七边形 C.正六边形 D.正五边形
【解答】解:A、正八边形的每个内角为:180°﹣360°÷8=135°,不能整除360°,不能密铺;
B、正七边形每个内角为:180°﹣360°÷7=900÷7,不能整除360°,不能密铺;
C、正六边形的每个内角是120°,能整除360°,能密铺;
D、正五边形的每个内角是108°,不能整除360°,不能密铺.
故选:C.
2.只用下列哪一种正多边形可以进行平面镶嵌( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
【解答】解:A、正五边形的每个内角度数为180°﹣360°÷5=108°,不能整除360°,不能进行平面镶嵌,不符合题意;
B、正六边形的每个内角度数为180°﹣360°÷6=120°,能整除360°,能进行平面镶嵌,符合题意;
C、正八边形的每个内角度数为180°﹣360°÷8=135°,不能整除360°,不能进行平面镶嵌,不符合题意;
D、正十边形的每个内角度数为180°﹣360°÷10=144°,不能整除360°,不能进行平面镶嵌,不符合题意;
故选:B.
3.若铺满地面的瓷砖每一个顶点处由6块相同的正多边形组成,此时的正多边形只能是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
【解答】解:A、6个正三角形满足同一顶点处的周角为360°,故本选项正确;
B、6个正四边形不满足同一顶点处的周角为360°,故本选项错误;
C、6个正六边形不满足同一顶点处的周角为360°,故本选项错误;
D、6个正八边形不满足同一顶点处的周角为360°,故本选项错误;
故选:A.
4.某家庭装修新房,下列组合不能够无缝隙不重叠铺设美丽地板的是( )
A.正三角形和正六边形
B.正五边形和正十边形
C.正方形和正八边形
D.正三角形、正六边形和正方形
【解答】解:∵用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.
∴为了能够做到无缝隙、不重叠地铺设,购买的地板砖形状不能是正五边形和正十边形.
故选:B.
5.用边长相等的下列两种正多边形,不能进行平面镶嵌的是( )
A.等边三角形和正六边形 B.正方形和正八边形
C.正五边形和正十边形 D.正六边形和正十二边形
【解答】解:A、正三角形的每个内角是60°,正六边形的每个内角是120°,∵2×60°+2×120°=360°,能密铺,故此选项不合题意;
B、正八边形的每个内角是135°,正方形的每个内角是90°,∵2×135°+90°=360°,能密铺,故此选项不合题意;
C、正五形的每个内角是108°,正十边形的每个内角是144°,∵2×108°+144°=360°,能密铺,故此选项不合题意;
D、正六边形的每个内角是120°和正十二边形的每个内角是150°,120m+150n=360°,m=3﹣n,显然n取任何正整数时,m不能得正整数,故不能铺满,符合题意.
故选:D.
6.利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0),则a+b的值为( )
A.3或4 B.4或5 C.5或6 D.4
【解答】解:∵正三边形和正六边形内角分别为60°、120°,
60°×4+120°=360°,或60°×2+120°×2=360°,
∴a=4,b=1或a=2,b=2,
①当a=4,b=1时,a+b=5;
②当a=2,b=2时,a+b=4.
故选:B.
7.用两种正多边形组合铺满地面,其中的一种是正八边形,则另一种是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
【解答】解:正八边形的一个内角=180°﹣=135°,
360°﹣2×135°=90°,
∵正方形的每个内角是90°,
∴另一种是正方形.
故选:B.
8.用两种正多边形镶嵌,不能与正三角形匹配的正多边形是( )
A.正方形 B.正六边形 C.正十二边形 D.正十八边形
【解答】解:A、正三角形的每个内角是60°,正方形的每个内角是90°.∵3×60°+2×90°=360°,∴正方形能匹配;
B、正六边形的每个内角是120°,正三角形的每个内角是60度.∵2×120°+2×60°=360°,或120°+4×60°=360°,∴正六边形能匹配;
C、正三角形的每个内角是60°,正十二边形的每个内角是180°﹣360°÷12=150°,∵60°+2×150°=360°,∴正十二边形能匹配;
D、正三角形的每个内角是60°,正十八边形内角为160°,显然不能构成360°的周角,故不能匹配.
故选:D.
9.下列组合不能密铺平面的是( )
A.正三角形、正方形和正六边形
B.正三角形、正方形和正十二边形
C.正三角形、正六边形和正十二边形
D.正方形、正六边形和正十二边形
【解答】解:A、正三角形、正方形和正六边形,可以密铺平面,比如:2个正方形,一个正六边形,一个正三角形.本选项不符合题意;
B、正三角形、正方形和正十二边形,可以密铺平面,比如:2个正三角形、一个正方形、一个正十二边形.本选项不符合题意;
C、正三角形、正六边形和正十二边形,不能密铺平面.本选项符合题意;
D、正方形、正六边形和正十二边形.可以密铺平面,比如:一个正方形、一个正六边形、一个正十二边形.本选项不符合题意;
故选:C.
10.下列每组图形,不能镶嵌整个平面的是( )
A. B.
C. D.
【解答】解:A、2个三角形2个正六边形或4个三角形1个正六边形可以镶嵌.本选项不符合题意.
B、1个右边的图和4个左边的图,可以镶嵌.本选项不符合题意.
C、正方形的内角为90°,矩形的内角为90°,可以镶嵌.本选项不符合题意.
D、正方形与正六边形,不可以镶嵌.本选项符合题意.
故选:D.
二.填空题(共7小题)
11.在下面的多边形中:①正三角形;②正方形;③正五边形;④正六边形,如果只用一种正多边形进行镶嵌,那么不能镶嵌成一个平面的有 ③ (只填序号)
【解答】解:①正三角形的每个内角是60°,能整除360°,能密铺;
②正方形的每个内角是90°,4个能密铺;
③正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺;
④正六边形的每个内角是120°,3个能密铺,
故不能镶嵌成一个平面的有③.
故答案为:③.
12.用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y= 11 .
【解答】解:要拼接成周长等于18的拼接图形,需要4或5或6或7个单位六边形.
故x=4,y=7,
则x+y=11.
故答案为:11.
13.如图,用三个完全相同的正五边形地砖平铺地面,则空余的角度是 36 度.
【解答】解:∵正五边形每个内角是180°﹣360°÷5=108°,
∴空余的角度=360°﹣3×108°=36°.
14.王老师家准备用边长相等的正四边形和正八边形的地面砖铺客厅,铺设图案如图所示.购买这两种正多边形地砖的数量之比约为 1:1 .
【解答】解:由铺设图案和镶嵌的条件可知购买边长相等的正四边形和正八边形这两种正多边形地砖的数量之比约为1:1.
15.用三块正多边形的木板铺地,拼在一起并相交于一点的各边完全吻合,若其中两块木板的边数均为5,则第三块木板的边数为 10 .
【解答】解:正五边形每个内角是180°﹣360°÷5=108°,顶点处已经有2个内角,度数之和为:108×2=216°,
那么另一个多边形的内角度数为:360°﹣216°=144°,
相邻的外角为:180°﹣144°=36°,
∴边数为:360°÷36°=10.
16.我们知道形状为正五边形的地砖不能铺满地面,但某公园的一段路面是用型号相同的特殊的五边形地砖铺成的.如图,是拼铺图案的一部分,其中每个五边形有3个内角相等,那么这3个内角都等于 120 度.
【解答】解:因为3个内角放在同一顶点处,组成一个周角,所以每个内角为:360°÷3=120°.
故这3个内角都等于120度.
17.如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖密铺,从里向外共铺了10层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第10层的外边界所围成的多边形的周长是 33 m.
【解答】解:根据题意分析可得:从里向外的第1层是6×2+6=18边形.
第2层是6×3+6=24边形.
此后,每层都比前一层多6条边.
依此递推,第10层是6×10+6=66边形.
∵边长为0.5m,∴第10层的外边界所围成的多边形的周长是66×0.5=33m.
故应填:33.
三.解答题(共3小题)
18.正三角形,正四边形可以铺满地面,但正十二边形和正八边形均不能铺满地面.试问,
(1)正三角形和正十二边形的结合能否铺满地面?如果可以,举例说明;如果不行,说明理由.
(2)由正四边形和正八变形组合呢?
【解答】解:(1)∵正三角形的每个内角是60°,正十二边形的每个内角是150°,
又∵60°+2×150°=360°,
∴用1个正三角形和2个正十二边形的结合能铺满地面;
(2)∵正四边形的每个内角是90°,正八边形的每个内角是135°,
又∵90°+2×135°=360°,
∴正四边形和正八边形组合能铺满地面.
19.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫作平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
正多边形的边数 3 4 5 6 8
正多边形每个内角的度数 60° 90° 108° 120° 135°
(1)填写表中空格.
(2)根据题意,如果仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)假设在镶嵌的平面图形的一个顶点周围有m个正四边形、n个正八边形,求m和n的值,请写出过程.
【解答】解:(1)正五边形每个内角的度数为:;
正六边形每个内角的度数为:;
正八边形每个内角的度数为:;
(2)因为,,,,,
所以仅用一种正多边形镶嵌,正三角形、正四边形、正六边形能镶嵌成一个平面图形;
(3)根据题意知90°m+135°n=360°,且m,n均为正整数,
即m,n是方程2m+3n=8的正整数解,
当m=1时,n=2,满足题意;
当m=2时,n=,不满足题意.
所以m=1,n=2.
20.小明家准备装修厨房,打算铺设如图1的正方形地砖,该地砖既是轴对称图形也是中心对称图形,铺设效果如图2所示.经测量图1发现,砖面上四个小正方形的边长都是4cm,AB=JN=2cm,中间的多边形CDEFGHIK是正八边形.
(1)求MA的长度;
(2)求正八边形CDEFGHIK的面积;
(3)已知小明家厨房的地面是边长为3.14米的正方形,用该地砖铺设完毕后,最多形成多少个正八边形?(地砖间缝隙的宽度忽略不计)
【解答】解:(1)连接BK和NC,两线的交点为O,
∵四边形BCKN是正方形,
∴∠NOB=90°,OB=ON,
∵BN=4cm,
∴由勾股定理得:BO=ON=2cm,
∵JN=2cm,
∴AM=JO=(2+2)cm;
(2)如图,作小正方形的对角线,组成正方形ORZQ,
则正方形的边长为(2+4+2)cm,即为(4+4)cm,
所以正八边形CDEFGHIK的面积为S正方形OQZR﹣4S△BOC=(4+4)2﹣4××2×2=(32+32)cm2;
(3)正方形地砖的边长为:2×(2+2)cm+(4+4)cm=(8+8)cm,
∵3.14米=314cm,
∴3142÷(8+8)2≈264,
∵162<264,
∴用该地砖铺设完毕后,最多形成32×32=1024个正八边形.
第1页(共1页)
