9.2.1多边形内角和练习2021-2022学年华东师大版数学七年级下册 (word版含答案)
文档属性
| 名称 | 9.2.1多边形内角和练习2021-2022学年华东师大版数学七年级下册 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 08:10:40 | ||
图片预览


文档简介
9.2.1多边形内角和
★如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
★n边形的内角为
★推导:从 n 边形的一个顶点出发,与不相邻的顶点可作(n-3)条对角线,将 n 边形分成(n-2)个三角形,每个三角形的内角和为,所以 n 边形的内角和为
★注:(1)多边形的内角和是指n个内角的度数之和;
多边形的内角和为,且内角和为的整数倍;
由多边形的边数可以求出其内角和,由多边形的内角和也可以求出多边形的边数.
★一个n边形截去一个角后边数会有三种情况:
①可能不变;②可能比原来多一条边;③可能比原来少一条边。由截的位置不同决定的.
一.选择题(共9小题)
1.一个多边形的内角和是1080°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则这个n边形的内角和为( )
A.720° B.900° C.1080° D.1260°
3.如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )
A.九边形 B.八边形 C.七边形 D.六边形
4.如图,该硬币边缘镌刻的正九边形每个内角的度数是( )
A.120° B.135° C.140° D.144°
5.从九边形的一个顶点出发,可以作①条对角线,它们将九边形分成②个三角形.对于符号①、②表示的数字正确的是( )
A.①6、②7 B.①7、②8 C.①8、②8 D.①9、②7
6.一个多边形的内角和等于1080°,这个多边形的边数为( )
A.9 B.6 C.7 D.8
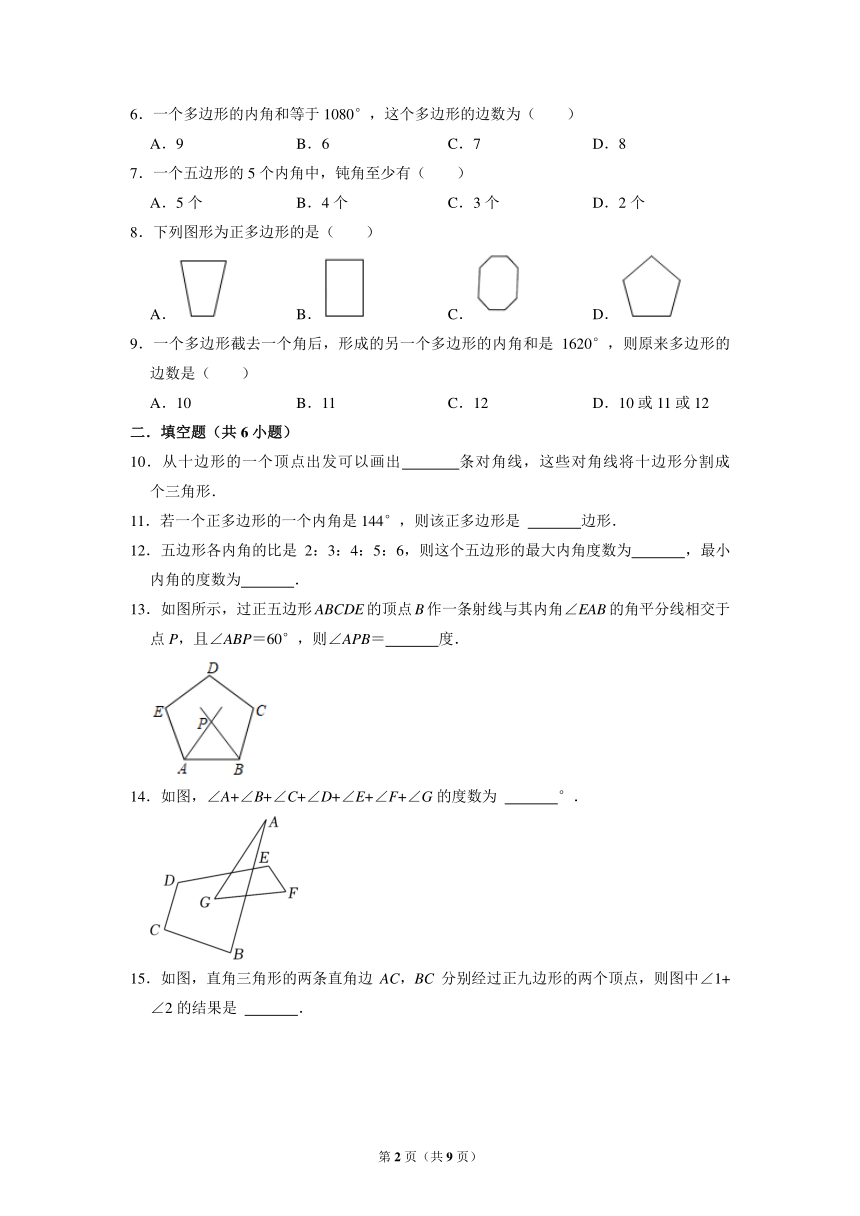
7.一个五边形的5个内角中,钝角至少有( )
A.5个 B.4个 C.3个 D.2个
8.下列图形为正多边形的是( )
A. B. C. D.
9.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
二.填空题(共6小题)
10.从十边形的一个顶点出发可以画出 条对角线,这些对角线将十边形分割成 个三角形.
11.若一个正多边形的一个内角是144°,则该正多边形是 边形.
12.五边形各内角的比是2:3:4:5:6,则这个五边形的最大内角度数为 ,最小内角的度数为 .
13.如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB= 度.
14.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 °.
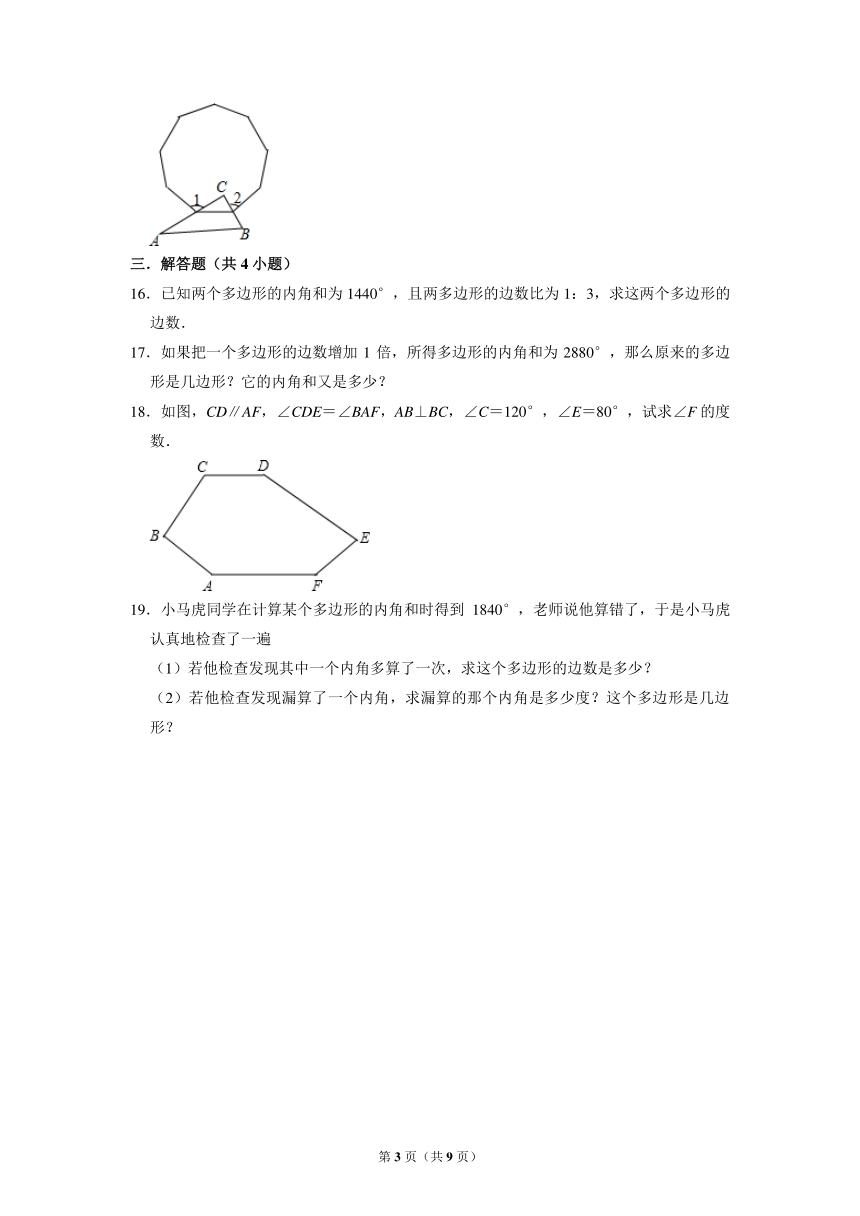
15.如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是 .
三.解答题(共4小题)
16.已知两个多边形的内角和为1440°,且两多边形的边数比为1:3,求这两个多边形的边数.
17.如果把一个多边形的边数增加1倍,所得多边形的内角和为2880°,那么原来的多边形是几边形?它的内角和又是多少?
18.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.
19.小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
9.2.1多边形内角和
参考答案与试题解析
一.选择题(共9小题)
1.一个多边形的内角和是1080°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
【解答】解:设所求n边形边数为n,
则1080°=(n﹣2) 180°,
解得n=8.
故选:B.
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则这个n边形的内角和为( )
A.720° B.900° C.1080° D.1260°
【解答】解:设多边形有n条边,
则n﹣2=6,
解得n=8.
180°×(8﹣2)=1080°,
故选:C.
3.如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )
A.九边形 B.八边形 C.七边形 D.六边形
【解答】解:∵过一个多边形的一个顶点的对角线有5条,
∴多边形的边数为5+3=8,
故选:B.
4.如图,该硬币边缘镌刻的正九边形每个内角的度数是( )
A.120° B.135° C.140° D.144°
【解答】解:∵正九边形的外角和为360°,
∴正九边形每个外角的度数是=40°,
∴正九边形每个内角的度数是180°﹣40°=140°.
故选:C.
5.从九边形的一个顶点出发,可以作①条对角线,它们将九边形分成②个三角形.对于符号①、②表示的数字正确的是( )
A.①6、②7 B.①7、②8 C.①8、②8 D.①9、②7
【解答】解:从九边形的一个顶点出发,可以向与这个顶点不相邻的6个顶点引对角线,即能引出6条对角线,它们将九边形分成7个三角形.
故选:A.
6.一个多边形的内角和等于1080°,这个多边形的边数为( )
A.9 B.6 C.7 D.8
【解答】解:设这个多边形边数为n,
则1080°=(n﹣2) 180°,
解得n=8.
故选:D.
7.一个五边形的5个内角中,钝角至少有( )
A.5个 B.4个 C.3个 D.2个
【解答】解:∵五边形外角和为360度,
∴5个外角中不能有4个或5个钝角,外角中至多有3个钝角,即内角中最多有3个锐角,至少有2个钝角.
故选:D.
8.下列图形为正多边形的是( )
A. B. C. D.
【解答】解:正五边形五个角相等,五条边都相等,
故选:D.
9.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
【解答】解:设多边形截去一个角的边数为n,
则(n﹣2) 180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
二.填空题(共6小题)
10.从十边形的一个顶点出发可以画出 7 条对角线,这些对角线将十边形分割成 8 个三角形.
【解答】解:从n边形的一个顶点出发可以引n﹣3条对角线,这些对角线将这个多边形分成n﹣2个三角形,
∴从十边形的一个顶点出发可以画出7条对角线,这些对角线将十边形分割成8个三角形.
故答案为:7;8.
11.若一个正多边形的一个内角是144°,则该正多边形是 10 边形.
【解答】解:该多边形的一个外角为:180°﹣144°=36°,
由外角和公式,可得该正多边形得边数为:360°÷36°=10.
故答案为:10.
12.五边形各内角的比是2:3:4:5:6,则这个五边形的最大内角度数为 162° ,最小内角的度数为 54° .
【解答】解:设五边形各内角的度数分别为2x°,3x°,4x°,5x°,6x°,
∴2x+3x+4x+5x+6x=(5﹣2)×180,
∴x=27,
∴6x=162,2x=54,
∴这个五边形的内角中最大和最小的度数分别为162°、54°.
13.如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB= 66 度.
【解答】解:∵五边形ABCDE为正五边形,
∴∠EAB=108度,
∵AP是∠EAB的角平分线,
∴∠PAB=54度,
∵∠ABP=60°,
∴∠APB=180°﹣60°﹣54°=66°.
故答案为:66.
14.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 540 °.
【解答】解:如图所示,
由三角形外角的性质可得,∠1=∠A+∠G,
由四边形的内角和是360°可得,
∠1+∠2+∠E+∠F=360°,∠3+∠B+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G
=∠1+∠C+∠D+∠E+∠F+∠B
=360°×2﹣180°
=540°.
故答案为:540.
15.如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是 190° .
【解答】解:如图,
(9﹣2)×180°÷9×2
=7×180°÷9×2
=280°,
∠3+∠4=180°﹣90°=90°,
∠1+∠2=280°﹣90°=190°.
故答案为:190°.
三.解答题(共4小题)
16.已知两个多边形的内角和为1440°,且两多边形的边数比为1:3,求这两个多边形的边数.
【解答】解:设两个多边形的边数分别是x和3x,
则(x﹣2) 180+(3x﹣2) 180=1440,
解之,得x=3,3x=9.
则两个多边形的边数分别为3和9.
17.如果把一个多边形的边数增加1倍,所得多边形的内角和为2880°,那么原来的多边形是几边形?它的内角和又是多少?
【解答】解:设原来的多边形为n边形,则边数增加1倍后为2n边形,
由(2n﹣2) 180°=2880°,
得n=9.
(9﹣2)×180°=1260°.
即原来的多边形为九边形,内角和为1260°.
18.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.
【解答】解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
∵AB⊥BC,
∴∠B=90°.
又∵∠C=120°,
∴∠BAD+∠ADC=150°.
∵CD∥AF,
∴∠CDA=∠DAF.
在四边形ADEF中,
∠DAF+∠EDA+∠F+∠E=360°,
∴∠F+∠E=210°.
又∵∠E=80°,
∴∠F=130°.
19.小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
【解答】解:(1)设这个多边形的边数是n,重复计算的内角的度数是x,
则(n﹣2) 180°=1840°﹣x,
n=12…40°.
故这个多边形的边数是12.
(2)设这个多边形的边数是n,没有计算在内的内角的度数是x,
则(n﹣2) 180°=1840°+x,
n=12…40°.
180°﹣40°=140°,
故漏算的那个内角是140度,这个多边形是十三边形.
第1页(共1页)
★如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
★n边形的内角为
★推导:从 n 边形的一个顶点出发,与不相邻的顶点可作(n-3)条对角线,将 n 边形分成(n-2)个三角形,每个三角形的内角和为,所以 n 边形的内角和为
★注:(1)多边形的内角和是指n个内角的度数之和;
多边形的内角和为,且内角和为的整数倍;
由多边形的边数可以求出其内角和,由多边形的内角和也可以求出多边形的边数.
★一个n边形截去一个角后边数会有三种情况:
①可能不变;②可能比原来多一条边;③可能比原来少一条边。由截的位置不同决定的.
一.选择题(共9小题)
1.一个多边形的内角和是1080°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则这个n边形的内角和为( )
A.720° B.900° C.1080° D.1260°
3.如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )
A.九边形 B.八边形 C.七边形 D.六边形
4.如图,该硬币边缘镌刻的正九边形每个内角的度数是( )
A.120° B.135° C.140° D.144°
5.从九边形的一个顶点出发,可以作①条对角线,它们将九边形分成②个三角形.对于符号①、②表示的数字正确的是( )
A.①6、②7 B.①7、②8 C.①8、②8 D.①9、②7
6.一个多边形的内角和等于1080°,这个多边形的边数为( )
A.9 B.6 C.7 D.8
7.一个五边形的5个内角中,钝角至少有( )
A.5个 B.4个 C.3个 D.2个
8.下列图形为正多边形的是( )
A. B. C. D.
9.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
二.填空题(共6小题)
10.从十边形的一个顶点出发可以画出 条对角线,这些对角线将十边形分割成 个三角形.
11.若一个正多边形的一个内角是144°,则该正多边形是 边形.
12.五边形各内角的比是2:3:4:5:6,则这个五边形的最大内角度数为 ,最小内角的度数为 .
13.如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB= 度.
14.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 °.
15.如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是 .
三.解答题(共4小题)
16.已知两个多边形的内角和为1440°,且两多边形的边数比为1:3,求这两个多边形的边数.
17.如果把一个多边形的边数增加1倍,所得多边形的内角和为2880°,那么原来的多边形是几边形?它的内角和又是多少?
18.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.
19.小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
9.2.1多边形内角和
参考答案与试题解析
一.选择题(共9小题)
1.一个多边形的内角和是1080°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
【解答】解:设所求n边形边数为n,
则1080°=(n﹣2) 180°,
解得n=8.
故选:B.
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则这个n边形的内角和为( )
A.720° B.900° C.1080° D.1260°
【解答】解:设多边形有n条边,
则n﹣2=6,
解得n=8.
180°×(8﹣2)=1080°,
故选:C.
3.如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )
A.九边形 B.八边形 C.七边形 D.六边形
【解答】解:∵过一个多边形的一个顶点的对角线有5条,
∴多边形的边数为5+3=8,
故选:B.
4.如图,该硬币边缘镌刻的正九边形每个内角的度数是( )
A.120° B.135° C.140° D.144°
【解答】解:∵正九边形的外角和为360°,
∴正九边形每个外角的度数是=40°,
∴正九边形每个内角的度数是180°﹣40°=140°.
故选:C.
5.从九边形的一个顶点出发,可以作①条对角线,它们将九边形分成②个三角形.对于符号①、②表示的数字正确的是( )
A.①6、②7 B.①7、②8 C.①8、②8 D.①9、②7
【解答】解:从九边形的一个顶点出发,可以向与这个顶点不相邻的6个顶点引对角线,即能引出6条对角线,它们将九边形分成7个三角形.
故选:A.
6.一个多边形的内角和等于1080°,这个多边形的边数为( )
A.9 B.6 C.7 D.8
【解答】解:设这个多边形边数为n,
则1080°=(n﹣2) 180°,
解得n=8.
故选:D.
7.一个五边形的5个内角中,钝角至少有( )
A.5个 B.4个 C.3个 D.2个
【解答】解:∵五边形外角和为360度,
∴5个外角中不能有4个或5个钝角,外角中至多有3个钝角,即内角中最多有3个锐角,至少有2个钝角.
故选:D.
8.下列图形为正多边形的是( )
A. B. C. D.
【解答】解:正五边形五个角相等,五条边都相等,
故选:D.
9.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
【解答】解:设多边形截去一个角的边数为n,
则(n﹣2) 180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
二.填空题(共6小题)
10.从十边形的一个顶点出发可以画出 7 条对角线,这些对角线将十边形分割成 8 个三角形.
【解答】解:从n边形的一个顶点出发可以引n﹣3条对角线,这些对角线将这个多边形分成n﹣2个三角形,
∴从十边形的一个顶点出发可以画出7条对角线,这些对角线将十边形分割成8个三角形.
故答案为:7;8.
11.若一个正多边形的一个内角是144°,则该正多边形是 10 边形.
【解答】解:该多边形的一个外角为:180°﹣144°=36°,
由外角和公式,可得该正多边形得边数为:360°÷36°=10.
故答案为:10.
12.五边形各内角的比是2:3:4:5:6,则这个五边形的最大内角度数为 162° ,最小内角的度数为 54° .
【解答】解:设五边形各内角的度数分别为2x°,3x°,4x°,5x°,6x°,
∴2x+3x+4x+5x+6x=(5﹣2)×180,
∴x=27,
∴6x=162,2x=54,
∴这个五边形的内角中最大和最小的度数分别为162°、54°.
13.如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB= 66 度.
【解答】解:∵五边形ABCDE为正五边形,
∴∠EAB=108度,
∵AP是∠EAB的角平分线,
∴∠PAB=54度,
∵∠ABP=60°,
∴∠APB=180°﹣60°﹣54°=66°.
故答案为:66.
14.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 540 °.
【解答】解:如图所示,
由三角形外角的性质可得,∠1=∠A+∠G,
由四边形的内角和是360°可得,
∠1+∠2+∠E+∠F=360°,∠3+∠B+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G
=∠1+∠C+∠D+∠E+∠F+∠B
=360°×2﹣180°
=540°.
故答案为:540.
15.如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是 190° .
【解答】解:如图,
(9﹣2)×180°÷9×2
=7×180°÷9×2
=280°,
∠3+∠4=180°﹣90°=90°,
∠1+∠2=280°﹣90°=190°.
故答案为:190°.
三.解答题(共4小题)
16.已知两个多边形的内角和为1440°,且两多边形的边数比为1:3,求这两个多边形的边数.
【解答】解:设两个多边形的边数分别是x和3x,
则(x﹣2) 180+(3x﹣2) 180=1440,
解之,得x=3,3x=9.
则两个多边形的边数分别为3和9.
17.如果把一个多边形的边数增加1倍,所得多边形的内角和为2880°,那么原来的多边形是几边形?它的内角和又是多少?
【解答】解:设原来的多边形为n边形,则边数增加1倍后为2n边形,
由(2n﹣2) 180°=2880°,
得n=9.
(9﹣2)×180°=1260°.
即原来的多边形为九边形,内角和为1260°.
18.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.
【解答】解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
∵AB⊥BC,
∴∠B=90°.
又∵∠C=120°,
∴∠BAD+∠ADC=150°.
∵CD∥AF,
∴∠CDA=∠DAF.
在四边形ADEF中,
∠DAF+∠EDA+∠F+∠E=360°,
∴∠F+∠E=210°.
又∵∠E=80°,
∴∠F=130°.
19.小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
【解答】解:(1)设这个多边形的边数是n,重复计算的内角的度数是x,
则(n﹣2) 180°=1840°﹣x,
n=12…40°.
故这个多边形的边数是12.
(2)设这个多边形的边数是n,没有计算在内的内角的度数是x,
则(n﹣2) 180°=1840°+x,
n=12…40°.
180°﹣40°=140°,
故漏算的那个内角是140度,这个多边形是十三边形.
第1页(共1页)
