2.7正方形同步优生辅导测评2021-2022学年湘教版八年级数学下册 (word版含答案)
文档属性
| 名称 | 2.7正方形同步优生辅导测评2021-2022学年湘教版八年级数学下册 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 252.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 08:48:41 | ||
图片预览


文档简介
2021-2022学年湘教版八年级数学下册《2-7正方形》同步优生辅导测评(附答案)
一.选择题(共6小题,满分30分)
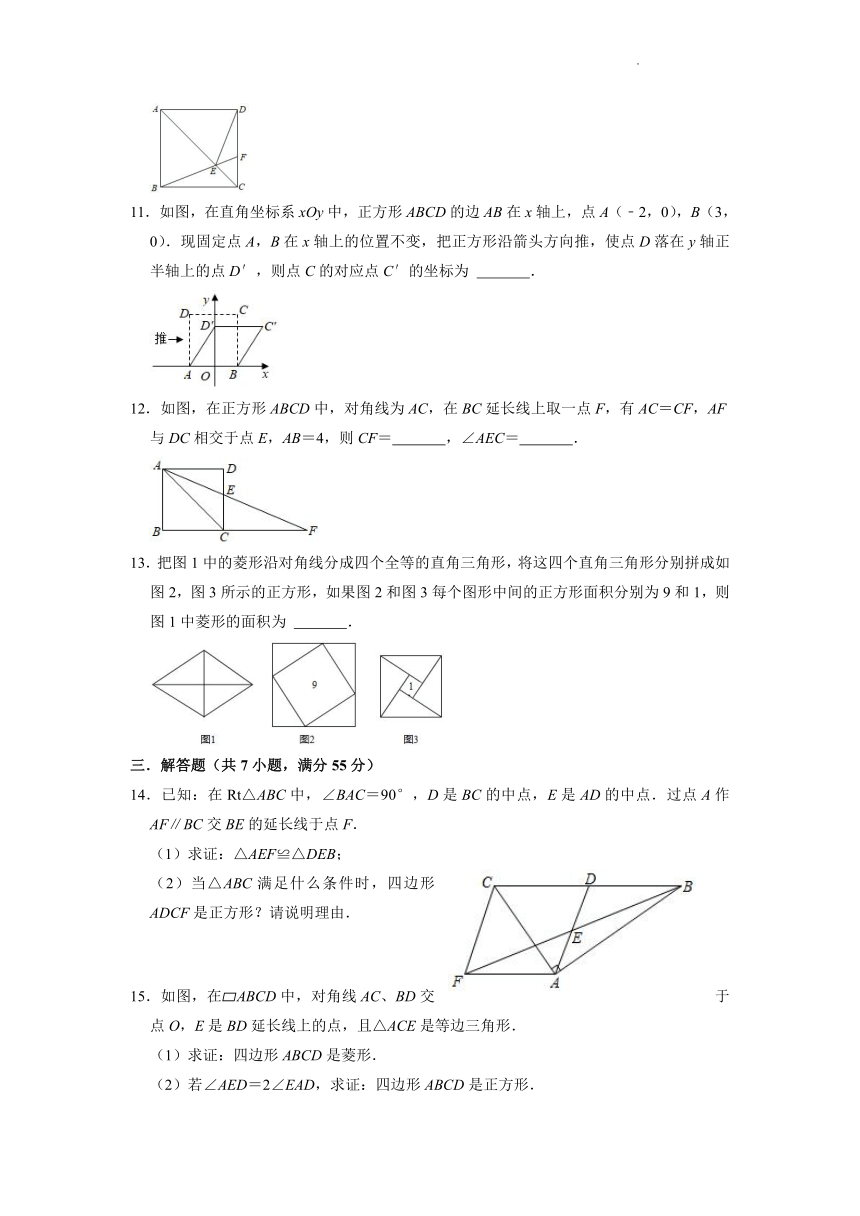
1.如图,四边形ABCD是平行四边形,从下列条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中,选出其中两个,使平行四边形ABCD变为正方形.下面组合错误的是( )
A.①② B.①③ C.③④ D.①④
2.如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.下列说法错误的是( )
A.若AC⊥BD,四边形ABCD是菱形
B.若AC=BD,四边形ABCD是矩形
C.若AB=BC且AC=BD,四边形ABCD是正方形
D.若∠ABC=90°,四边形ABCD是正方形
3.如图,延长正方形ABCD边B至点E,使AE=BD,则∠E为( )
A.22.5° B.25° C.30° D.45°
4.如图,在边长为6的正方形ABCD中,点P为对角线AC上一动点,PE⊥AB于E,PF⊥BC于F,则EF的最小值为( )
A. B. C.4 D.3
5.如图,正方形ABCD的边长为8,点E在对角线AC上,且∠EBC=22.5°,EF⊥BC于点F,则EF的长为( )
A.2 B.2 C. D.
6.如图,已知点E是正方形ABCD的边AD的延长线上一点,连接CE,过点A作AH⊥CE,交CD边于点F,垂足为点H,若DF=1,FC=2,则CE的长为( )
A. B. C. D.4
二.填空题(共7小题,满分35分)
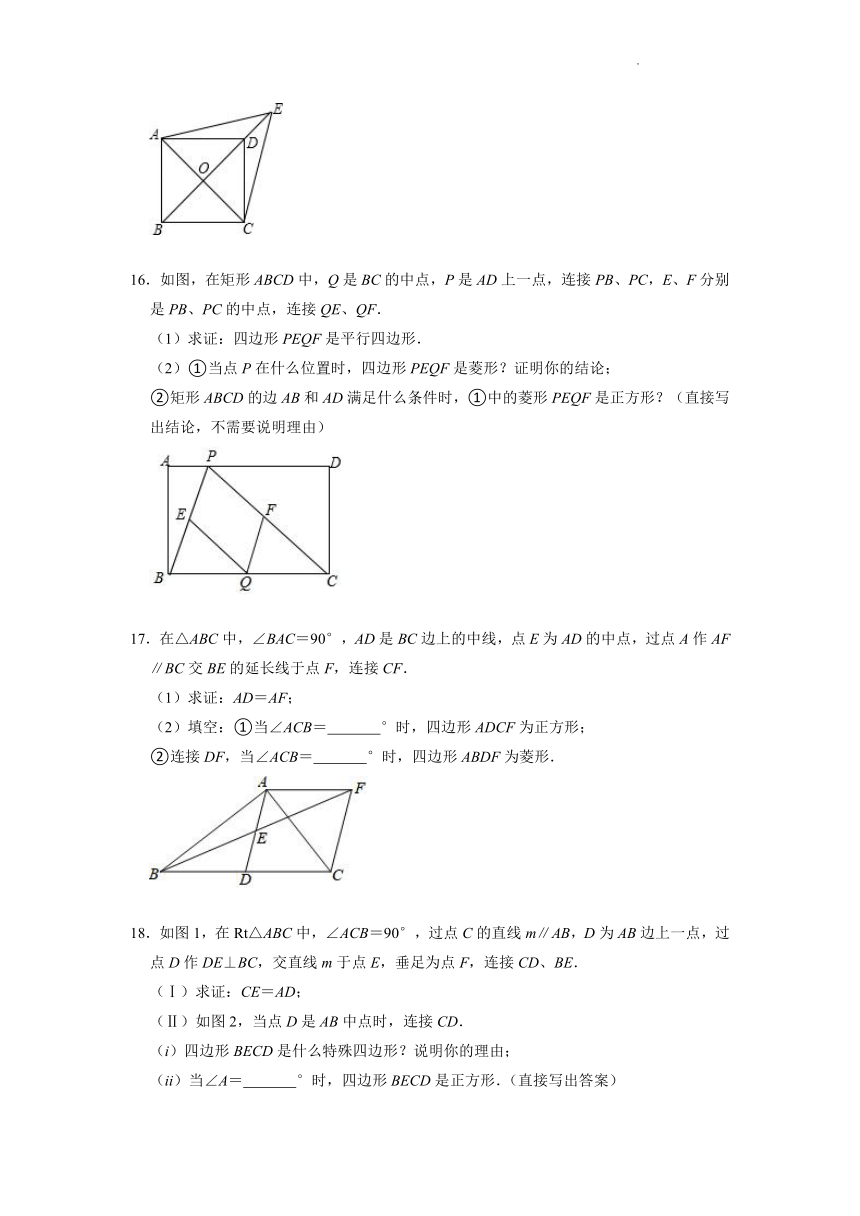
7.如图,四边形ABCD中,对角线AC,BD相交于点O,AD∥BC,OA=OC,AC平分∠BAD.欲使四边形ABCD是正方形,则还需添加添加 .(写出一个合适的条件即可)
8.如图,E是正方形ABCD的对角线BD上一点,连接CE,过点E作EF⊥AD,垂足为点F.若AF=3,EC=5,则正方形ABCD的面积为 .
9.在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4= .
10.如图,在正方形ABCD中,点F为边CD上一点,BF与AC交于点E.若∠CBF=25°,则∠AED的大小为 度.
11.如图,在直角坐标系xOy中,正方形ABCD的边AB在x轴上,点A(﹣2,0),B(3,0).现固定点A,B在x轴上的位置不变,把正方形沿箭头方向推,使点D落在y轴正半轴上的点D′,则点C的对应点C′的坐标为 .
12.如图,在正方形ABCD中,对角线为AC,在BC延长线上取一点F,有AC=CF,AF与DC相交于点E,AB=4,则CF= ,∠AEC= .
13.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,如果图2和图3每个图形中间的正方形面积分别为9和1,则图1中菱形的面积为 .
三.解答题(共7小题,满分55分)
14.已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
15.如图,在 ABCD中,对角线AC、BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
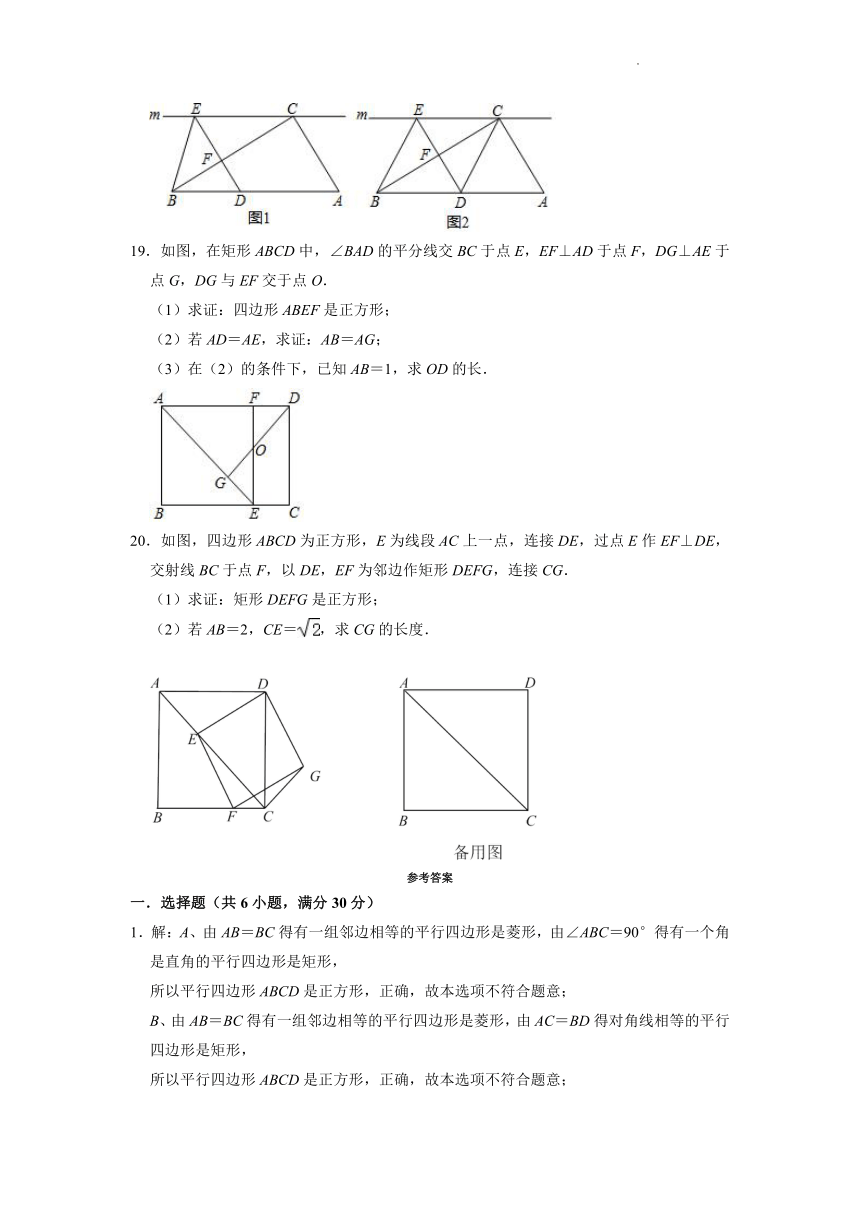
16.如图,在矩形ABCD中,Q是BC的中点,P是AD上一点,连接PB、PC,E、F分别是PB、PC的中点,连接QE、QF.
(1)求证:四边形PEQF是平行四边形.
(2)①当点P在什么位置时,四边形PEQF是菱形?证明你的结论;
②矩形ABCD的边AB和AD满足什么条件时,①中的菱形PEQF是正方形?(直接写出结论,不需要说明理由)
17.在△ABC中,∠BAC=90°,AD是BC边上的中线,点E为AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形ADCF为正方形;
②连接DF,当∠ACB= °时,四边形ABDF为菱形.
18.如图1,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD、BE.
(Ⅰ)求证:CE=AD;
(Ⅱ)如图2,当点D是AB中点时,连接CD.
(i)四边形BECD是什么特殊四边形?说明你的理由;
(ii)当∠A= °时,四边形BECD是正方形.(直接写出答案)
19.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
20.如图,四边形ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度.
参考答案
一.选择题(共6小题,满分30分)
1.解:A、由AB=BC得有一组邻边相等的平行四边形是菱形,由∠ABC=90°得有一个角是直角的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由AB=BC得有一组邻边相等的平行四边形是菱形,由AC=BD得对角线相等的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
C、由AC=BD得对角线相等的平行四边形是矩形,由AC⊥BD得对角线互相垂直的平行四边形是菱形,
所以能得出平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由AB=BC得有一组邻边相等的平行四边形是菱形,由AC⊥BD得对角线互相垂直的平行四边形是菱形,
所以不能得到平行四边形ABCD是正方形,错误,故本选项符合题意;
故选:D.
2.解:∵四边形ABCD的对角线AC,BD相交于点O,且OA=OC,OB=OD,
∴四边形ABCD为平行四边形.
A.∵AC⊥BD,
∴平行四边形ABCD是菱形,故该选项不符合题意;
B.∵AC=BD,
∴平行四边形ABCD是矩形,故该选项不符合题意;
C.∵AB=BC,
∴平行四边形ABCD是菱形,
∵AC=BD,
∴菱形ABCD是正方形;故该选项不符合题意;
D.∵∠ABC=90°,
∴平行四边形ABCD是矩形,故该选项符合题意;
故选:D.
3.解:连接AC,
∵四边形ABCD是正方形,
∴AC=BD,且∠CAB=45°,
又∵BD=AE,
∴AE=CA,
∴∠E=∠ACE,
∵∠CAB=∠ACE+∠E=2∠E=45°,
∴∠E=22.5°.
故选:A.
4.解:连接BP,如图,
,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=6,
∵PE⊥AB,PF⊥BC,
∴四边形PEBF为矩形,
∴EF=BP,
当BP⊥AC,BP最短,
在Rt△BPC中,BP=PC,BC=6,
根据勾股定理可解得BP=3,
∴EF得最小值为3.
故选:B.
5.解:∵四边形ABCD是正方形,
∴∠BAC=∠ACB=45°,∠ABC=90°,
∵AB=8,
∴AC=8,
∵∠EBC=22.5°,
∴∠ABE=67.5°,
∴∠AEB=180°﹣67.5°﹣45°=67.5°,
∴∠ABE=∠AEB,
∴AE=AB=8,
∴CE=AC﹣AE=8﹣8,
∵EF⊥BC,
∴△CEF是等腰直角三角形,
∴EF=CE=8﹣4,
故选:C.
6.解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠CDE=90°=∠ADC,
∵AH⊥CE,
∴∠AHC=90°,
∴∠DAF+∠AFD=90°,∠DCE+∠CFH=90°,
∵∠AFD=∠CFH,
∴∠DAF=∠DCE,
在△ADF和△CDE中,
,
∴△ADF≌△CDE(ASA),
∴DF=DE,
∵DF=1,
∴DE=1,
∵CF=2,
∴DC=1+2=3,
在Rt△CDE中,由勾股定理得:CE===,
故选:B.
二.填空题(共7小题,满分35分)
7.解:∵AD∥BC,
∴∠DAO=∠BCO,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴OB=OD,
∵OA=OC,
∴四边形ABCD为平行四边形,
∵AC平分∠BAD
∴∠DAC=∠BAC,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠BCA,
∴BA=BC,
∴四边形ABCD为菱形,
∴当AC=BD或∠BAD=90°,四边形ABCD为正方形,
故答案为:AC=BD或∠BAD=90°.
8.解:连接AE,
∵正方形ABCD,
∴AB=BC,∠ABD=∠CBD=45°,
∵BE=BE,
∴△ABE≌△CBE,
∴AE=EC=5,
∵EF⊥AD,若AF=3,
∴EF==4,
∴DF=4,AD=4+3=7,
∴正方形ABCD的面积为49,
故答案为:49.
9.解:如图,∵图中的四边形为正方形,
∴∠ABD=90°,AB=DB,
∴∠ABC+∠DBE=90°,
∵∠ABC+∠CAB=90°,
∴∠CAB=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AC=BE,
∵DE2+BE2=BD2,
∴ED2+AC2=BD2,
∵S1=AC2,S2=DE2,BD2=1,
∴S1+S2=1,
同理可得S3+S4=3,
∴S1+S2+S3+S4=1+3=4.
故答案为4.
10.解:∵四边形ABCD是正方形,且AC为正方ABCD的对角线,
∴△ABE与△ADE关于直线AC对称,∠ACB=45°,
∴∠AED=∠AEB,
∵∠AEB为△EBC的外角,
∴∠AEB=∠CBE+∠ACB=25°+45°=70°,
∴∠AED=70°,
故答案为70.
11.解:∵点A(﹣2,0),B(3,0),
∴AB=5,
∵四边形ABCD是正方形,
∴AD′=AD=AB=5,
∵AO=2,
∴OD′===,
∵C′D′=5,C′D′∥AB,
∴C′(5,),
故答案为:(5,).
12.解:∵四边形ABCD是正方形,
∴AB=BC=4,∠ACB=45°,
∴AC=4,
∴CF=AC=4,
∴∠CAF=∠CFA=22.5°,
∴∠AEC=∠CFA+∠DCF=112.5°,
故答案为4,112.5°.
13.解:设菱形中的直角三角形较长的直角边为a,较短的直角边为b,
则:,
化简得:ab=4,
∴菱形的面积为,
故答案为8.
三.解答题(共7小题,满分55分)
14.(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
(2)解:当AB=AC时,四边形ADCF是正方形,
理由:由(1)知,△AEF≌△DEB,
∴AF=DB,
∵D是BC的中点,
∴DB=DC,
∴AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=BC,
∴四边形ADCF是菱形,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴四边形ADCF是正方形.
15.证明:(1)∵ ABCD,
∴AO=OC,
∵△ACE是等边三角形,
∴EO⊥AC (三线合一)
即 BD⊥AC,
∴ ABCD是菱形;
(2)∵△ACE是等边三角形,∠EAC=60°
由(1)知,EO⊥AC,AO=OC
∴∠AEO=∠OEC=30°,△AOE是直角三角形
∴∠EAO=60°,
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠DAO=∠EAO﹣∠EAD=45°,
∵ ABCD是菱形,
∴∠BAD=2∠DAO=90°,
∴菱形ABCD是正方形.
16.(1)证明:在△PBC中,E、F分别是PB、PC的中点,Q是BC的中点,
∴QE、QF为△PBC的中位线,
∴QE∥PF,QF∥PE,
∴四边形PEQF是平行四边形;
(2)解:①当点P为AD的中点时,四边形PEQF是菱形,
理由是:当P为AD的中点时,AP=PD,
由勾股定理得:PB=,
PC=,
∵四边形ABCD是矩形,
∴AB=CD,
∴PB=PC,
∵E、F分别是PB、PC的中点,
∴PE=PF,
由(1)知:四边形PEQF是平行四边形,
∴四边形PEQF是菱形;
②矩形ABCD的边AB和AD满足AD=2AB时,①中的菱形PEQF是正方形,
理由是:∵AD=2AB,AD=2AP,
∴AB=AP,
∴△ABP是等腰直角三角形,
∴∠APB=45°,
同理可得∠CPD=45°,
∴∠EPF=90°,
∴①中的菱形PEQF是正方形.
17.(1)证明:∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)解:①∵AF∥CD,AF=CD,AD=AF,
∴四边形ADCF是菱形,
当四边形ADCF为正方形时,∠DCF=90°,
∴∠ACB=∠ACF=45°;
②∴CD=CF,
当四边形ABCF为菱形时,BD=DF,则DC=DF,
∴CD=CF=DF,
∴△DCF为等边三角形,
∴∠DCF=60°,
∴∠ACB=∠ACF=30°.
故答案为:45,30.
18.解:(Ⅰ)证明:连接CD,
∵m∥AB,
∴EC∥AD
∵DE⊥BC,∴∠CFD=90°,
∵∠BCD+∠DCA=90°,∠BCD+∠CDE=90°,
∴∠DCA=∠CDE,
∴DE∥AC
∴四边形DECA是平行四边形,
∴CE=DA
(Ⅱ)(i)四边形BECD是菱形.
∵由(Ⅰ)知:四边形DECA是平行四边形,
∴CE=DA,CE∥AD
在Rt△ABC中,∵点D是AB的中点,
∴BD=DC=DA,
又∵CE=DA,CE∥AD
∴四边形BECD是菱形.
(ii)当∠A=45°时,
由于四边形DECA是平行四边形,
∴∠EDB=∠A=45°,
又∵BE=BD,
∴∠BED=∠EDB=45°,
∴∠EBD=90°.
由于四边形BECD是菱形,
∴四边形BECD是正方形.
故答案为:45°
19.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DO=OF=OG,
∴DG=DO+OG=OG+OG=1,
∴OG==﹣1,
∴OD=(﹣1)=2﹣.
20.(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED,
在△EQF和△EPD中,
,
∴△EQF≌△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2中,在Rt△ABC中,AC=AB=2,
∵CE=,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,
∴四边形DECG是正方形,
∴CG=CE=.
一.选择题(共6小题,满分30分)
1.如图,四边形ABCD是平行四边形,从下列条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中,选出其中两个,使平行四边形ABCD变为正方形.下面组合错误的是( )
A.①② B.①③ C.③④ D.①④
2.如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.下列说法错误的是( )
A.若AC⊥BD,四边形ABCD是菱形
B.若AC=BD,四边形ABCD是矩形
C.若AB=BC且AC=BD,四边形ABCD是正方形
D.若∠ABC=90°,四边形ABCD是正方形
3.如图,延长正方形ABCD边B至点E,使AE=BD,则∠E为( )
A.22.5° B.25° C.30° D.45°
4.如图,在边长为6的正方形ABCD中,点P为对角线AC上一动点,PE⊥AB于E,PF⊥BC于F,则EF的最小值为( )
A. B. C.4 D.3
5.如图,正方形ABCD的边长为8,点E在对角线AC上,且∠EBC=22.5°,EF⊥BC于点F,则EF的长为( )
A.2 B.2 C. D.
6.如图,已知点E是正方形ABCD的边AD的延长线上一点,连接CE,过点A作AH⊥CE,交CD边于点F,垂足为点H,若DF=1,FC=2,则CE的长为( )
A. B. C. D.4
二.填空题(共7小题,满分35分)
7.如图,四边形ABCD中,对角线AC,BD相交于点O,AD∥BC,OA=OC,AC平分∠BAD.欲使四边形ABCD是正方形,则还需添加添加 .(写出一个合适的条件即可)
8.如图,E是正方形ABCD的对角线BD上一点,连接CE,过点E作EF⊥AD,垂足为点F.若AF=3,EC=5,则正方形ABCD的面积为 .
9.在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4= .
10.如图,在正方形ABCD中,点F为边CD上一点,BF与AC交于点E.若∠CBF=25°,则∠AED的大小为 度.
11.如图,在直角坐标系xOy中,正方形ABCD的边AB在x轴上,点A(﹣2,0),B(3,0).现固定点A,B在x轴上的位置不变,把正方形沿箭头方向推,使点D落在y轴正半轴上的点D′,则点C的对应点C′的坐标为 .
12.如图,在正方形ABCD中,对角线为AC,在BC延长线上取一点F,有AC=CF,AF与DC相交于点E,AB=4,则CF= ,∠AEC= .
13.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,如果图2和图3每个图形中间的正方形面积分别为9和1,则图1中菱形的面积为 .
三.解答题(共7小题,满分55分)
14.已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
15.如图,在 ABCD中,对角线AC、BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
16.如图,在矩形ABCD中,Q是BC的中点,P是AD上一点,连接PB、PC,E、F分别是PB、PC的中点,连接QE、QF.
(1)求证:四边形PEQF是平行四边形.
(2)①当点P在什么位置时,四边形PEQF是菱形?证明你的结论;
②矩形ABCD的边AB和AD满足什么条件时,①中的菱形PEQF是正方形?(直接写出结论,不需要说明理由)
17.在△ABC中,∠BAC=90°,AD是BC边上的中线,点E为AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形ADCF为正方形;
②连接DF,当∠ACB= °时,四边形ABDF为菱形.
18.如图1,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD、BE.
(Ⅰ)求证:CE=AD;
(Ⅱ)如图2,当点D是AB中点时,连接CD.
(i)四边形BECD是什么特殊四边形?说明你的理由;
(ii)当∠A= °时,四边形BECD是正方形.(直接写出答案)
19.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
20.如图,四边形ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度.
参考答案
一.选择题(共6小题,满分30分)
1.解:A、由AB=BC得有一组邻边相等的平行四边形是菱形,由∠ABC=90°得有一个角是直角的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由AB=BC得有一组邻边相等的平行四边形是菱形,由AC=BD得对角线相等的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
C、由AC=BD得对角线相等的平行四边形是矩形,由AC⊥BD得对角线互相垂直的平行四边形是菱形,
所以能得出平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由AB=BC得有一组邻边相等的平行四边形是菱形,由AC⊥BD得对角线互相垂直的平行四边形是菱形,
所以不能得到平行四边形ABCD是正方形,错误,故本选项符合题意;
故选:D.
2.解:∵四边形ABCD的对角线AC,BD相交于点O,且OA=OC,OB=OD,
∴四边形ABCD为平行四边形.
A.∵AC⊥BD,
∴平行四边形ABCD是菱形,故该选项不符合题意;
B.∵AC=BD,
∴平行四边形ABCD是矩形,故该选项不符合题意;
C.∵AB=BC,
∴平行四边形ABCD是菱形,
∵AC=BD,
∴菱形ABCD是正方形;故该选项不符合题意;
D.∵∠ABC=90°,
∴平行四边形ABCD是矩形,故该选项符合题意;
故选:D.
3.解:连接AC,
∵四边形ABCD是正方形,
∴AC=BD,且∠CAB=45°,
又∵BD=AE,
∴AE=CA,
∴∠E=∠ACE,
∵∠CAB=∠ACE+∠E=2∠E=45°,
∴∠E=22.5°.
故选:A.
4.解:连接BP,如图,
,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=6,
∵PE⊥AB,PF⊥BC,
∴四边形PEBF为矩形,
∴EF=BP,
当BP⊥AC,BP最短,
在Rt△BPC中,BP=PC,BC=6,
根据勾股定理可解得BP=3,
∴EF得最小值为3.
故选:B.
5.解:∵四边形ABCD是正方形,
∴∠BAC=∠ACB=45°,∠ABC=90°,
∵AB=8,
∴AC=8,
∵∠EBC=22.5°,
∴∠ABE=67.5°,
∴∠AEB=180°﹣67.5°﹣45°=67.5°,
∴∠ABE=∠AEB,
∴AE=AB=8,
∴CE=AC﹣AE=8﹣8,
∵EF⊥BC,
∴△CEF是等腰直角三角形,
∴EF=CE=8﹣4,
故选:C.
6.解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠CDE=90°=∠ADC,
∵AH⊥CE,
∴∠AHC=90°,
∴∠DAF+∠AFD=90°,∠DCE+∠CFH=90°,
∵∠AFD=∠CFH,
∴∠DAF=∠DCE,
在△ADF和△CDE中,
,
∴△ADF≌△CDE(ASA),
∴DF=DE,
∵DF=1,
∴DE=1,
∵CF=2,
∴DC=1+2=3,
在Rt△CDE中,由勾股定理得:CE===,
故选:B.
二.填空题(共7小题,满分35分)
7.解:∵AD∥BC,
∴∠DAO=∠BCO,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴OB=OD,
∵OA=OC,
∴四边形ABCD为平行四边形,
∵AC平分∠BAD
∴∠DAC=∠BAC,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠BCA,
∴BA=BC,
∴四边形ABCD为菱形,
∴当AC=BD或∠BAD=90°,四边形ABCD为正方形,
故答案为:AC=BD或∠BAD=90°.
8.解:连接AE,
∵正方形ABCD,
∴AB=BC,∠ABD=∠CBD=45°,
∵BE=BE,
∴△ABE≌△CBE,
∴AE=EC=5,
∵EF⊥AD,若AF=3,
∴EF==4,
∴DF=4,AD=4+3=7,
∴正方形ABCD的面积为49,
故答案为:49.
9.解:如图,∵图中的四边形为正方形,
∴∠ABD=90°,AB=DB,
∴∠ABC+∠DBE=90°,
∵∠ABC+∠CAB=90°,
∴∠CAB=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AC=BE,
∵DE2+BE2=BD2,
∴ED2+AC2=BD2,
∵S1=AC2,S2=DE2,BD2=1,
∴S1+S2=1,
同理可得S3+S4=3,
∴S1+S2+S3+S4=1+3=4.
故答案为4.
10.解:∵四边形ABCD是正方形,且AC为正方ABCD的对角线,
∴△ABE与△ADE关于直线AC对称,∠ACB=45°,
∴∠AED=∠AEB,
∵∠AEB为△EBC的外角,
∴∠AEB=∠CBE+∠ACB=25°+45°=70°,
∴∠AED=70°,
故答案为70.
11.解:∵点A(﹣2,0),B(3,0),
∴AB=5,
∵四边形ABCD是正方形,
∴AD′=AD=AB=5,
∵AO=2,
∴OD′===,
∵C′D′=5,C′D′∥AB,
∴C′(5,),
故答案为:(5,).
12.解:∵四边形ABCD是正方形,
∴AB=BC=4,∠ACB=45°,
∴AC=4,
∴CF=AC=4,
∴∠CAF=∠CFA=22.5°,
∴∠AEC=∠CFA+∠DCF=112.5°,
故答案为4,112.5°.
13.解:设菱形中的直角三角形较长的直角边为a,较短的直角边为b,
则:,
化简得:ab=4,
∴菱形的面积为,
故答案为8.
三.解答题(共7小题,满分55分)
14.(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
(2)解:当AB=AC时,四边形ADCF是正方形,
理由:由(1)知,△AEF≌△DEB,
∴AF=DB,
∵D是BC的中点,
∴DB=DC,
∴AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=BC,
∴四边形ADCF是菱形,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴四边形ADCF是正方形.
15.证明:(1)∵ ABCD,
∴AO=OC,
∵△ACE是等边三角形,
∴EO⊥AC (三线合一)
即 BD⊥AC,
∴ ABCD是菱形;
(2)∵△ACE是等边三角形,∠EAC=60°
由(1)知,EO⊥AC,AO=OC
∴∠AEO=∠OEC=30°,△AOE是直角三角形
∴∠EAO=60°,
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠DAO=∠EAO﹣∠EAD=45°,
∵ ABCD是菱形,
∴∠BAD=2∠DAO=90°,
∴菱形ABCD是正方形.
16.(1)证明:在△PBC中,E、F分别是PB、PC的中点,Q是BC的中点,
∴QE、QF为△PBC的中位线,
∴QE∥PF,QF∥PE,
∴四边形PEQF是平行四边形;
(2)解:①当点P为AD的中点时,四边形PEQF是菱形,
理由是:当P为AD的中点时,AP=PD,
由勾股定理得:PB=,
PC=,
∵四边形ABCD是矩形,
∴AB=CD,
∴PB=PC,
∵E、F分别是PB、PC的中点,
∴PE=PF,
由(1)知:四边形PEQF是平行四边形,
∴四边形PEQF是菱形;
②矩形ABCD的边AB和AD满足AD=2AB时,①中的菱形PEQF是正方形,
理由是:∵AD=2AB,AD=2AP,
∴AB=AP,
∴△ABP是等腰直角三角形,
∴∠APB=45°,
同理可得∠CPD=45°,
∴∠EPF=90°,
∴①中的菱形PEQF是正方形.
17.(1)证明:∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)解:①∵AF∥CD,AF=CD,AD=AF,
∴四边形ADCF是菱形,
当四边形ADCF为正方形时,∠DCF=90°,
∴∠ACB=∠ACF=45°;
②∴CD=CF,
当四边形ABCF为菱形时,BD=DF,则DC=DF,
∴CD=CF=DF,
∴△DCF为等边三角形,
∴∠DCF=60°,
∴∠ACB=∠ACF=30°.
故答案为:45,30.
18.解:(Ⅰ)证明:连接CD,
∵m∥AB,
∴EC∥AD
∵DE⊥BC,∴∠CFD=90°,
∵∠BCD+∠DCA=90°,∠BCD+∠CDE=90°,
∴∠DCA=∠CDE,
∴DE∥AC
∴四边形DECA是平行四边形,
∴CE=DA
(Ⅱ)(i)四边形BECD是菱形.
∵由(Ⅰ)知:四边形DECA是平行四边形,
∴CE=DA,CE∥AD
在Rt△ABC中,∵点D是AB的中点,
∴BD=DC=DA,
又∵CE=DA,CE∥AD
∴四边形BECD是菱形.
(ii)当∠A=45°时,
由于四边形DECA是平行四边形,
∴∠EDB=∠A=45°,
又∵BE=BD,
∴∠BED=∠EDB=45°,
∴∠EBD=90°.
由于四边形BECD是菱形,
∴四边形BECD是正方形.
故答案为:45°
19.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DO=OF=OG,
∴DG=DO+OG=OG+OG=1,
∴OG==﹣1,
∴OD=(﹣1)=2﹣.
20.(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED,
在△EQF和△EPD中,
,
∴△EQF≌△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2中,在Rt△ABC中,AC=AB=2,
∵CE=,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,
∴四边形DECG是正方形,
∴CG=CE=.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
