2021-2022学年鲁教版(五四制)七年级数学下册8.6三角形内角和定理 优生辅导训练(word版 含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学下册8.6三角形内角和定理 优生辅导训练(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 299.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 08:49:49 | ||
图片预览




文档简介
2021-2022学年鲁教版七年级数学下册《8-6三角形内角和定理》优生辅导训练(附答案)
一.选择题
1.如图,在△ABC中,D在BC的延长线上,过D作DF⊥AB于F,交AC于E.已知∠A=35°,∠ECD=85°,则∠D=( )
A.30° B.40° C.45° D.50°
2.如图,∠A=α,∠DBC=3∠DBA,∠DCB=3∠DCA,则∠BDC的大小为( )
A. B. C. D.
3.在△ABC中,∠C=∠A+∠B,∠B=2∠A﹣12°,则∠B的度数为( )
A.78° B.58° C.56° D.34°
4.如图,AD是△ABC的角平分线,CE⊥AD,垂足为F.若∠CAB=40°,∠B=50°,则∠BDE的度数为( )
A.35° B.40° C.45° D.50°
5.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外面时,此时测得∠1=112°,∠A=40°,则∠2的度数为( )
A.32° B.33° C.34° D.38°
6.将一副三角板如图放置,∠FDE=∠A=90°,∠C=45°,∠E=60°,且点D在BC上,点B在EF上,AC∥EF,则∠FDC的度数为( )
A.150° B.160° C.165° D.155°
7.如图,已知AB,CD是两条相交线段,连结AD,CB,分别作∠DAB和∠BCD的平分线相交于点P,若∠D=50°,∠B=40°,则∠P的度数为( )
A.50° B.45° C.40° D.30°
8.有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C,在△ABC中,∠DBA+∠DCA=n°,则∠A的度数是( )
A.90°+n° B.45°+n° C.90°﹣n° D.180°﹣n°
9.如图,延长△ABC的边AC到点E,过点E作DE∥BC,BG平分∠ABC,EF平分∠AED交BG的反向延长找于点F.已知3∠A=4∠F,则∠A的大小为( )
A.75° B.74° C.72° D.70°
10.如图,小明从一张三角形纸片ABC的AC边上选取一点N,将纸片沿着BN对折一次使得点A落在A′处后,再将纸片沿着BA′对折一次,使得点C落在BN上的C′处,已知∠CMB=68°,∠A=18°,则原三角形的∠C的度数为( )
A.87° B.84° C.75° D.72°
11.如图,在直角△ABC中,∠CAB=90°,∠ABC=70°,AD是∠CAB的平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( )
A.35° B.30° C.25° D.20°
12.如图,△ABC中,∠ABC、∠ACB的三等分线交于点E、D,若∠E=90°,则∠BDC的度数为( )
A.120° B.125° C.130° D.135°
二.填空题
13.如图,线段AF⊥AE,垂足为点A,线段GD分别交AF、AE于点C,B,连结GF,ED.则∠D+∠G+∠AFG+∠AED的度数为 .
14.如图,△ABC中,∠A=60°,∠B=50°,D、E分别是AB、AC上两点,连接DE并延长,交BC的延长线于点F,此时,∠F=35°,则∠1的度数为 .
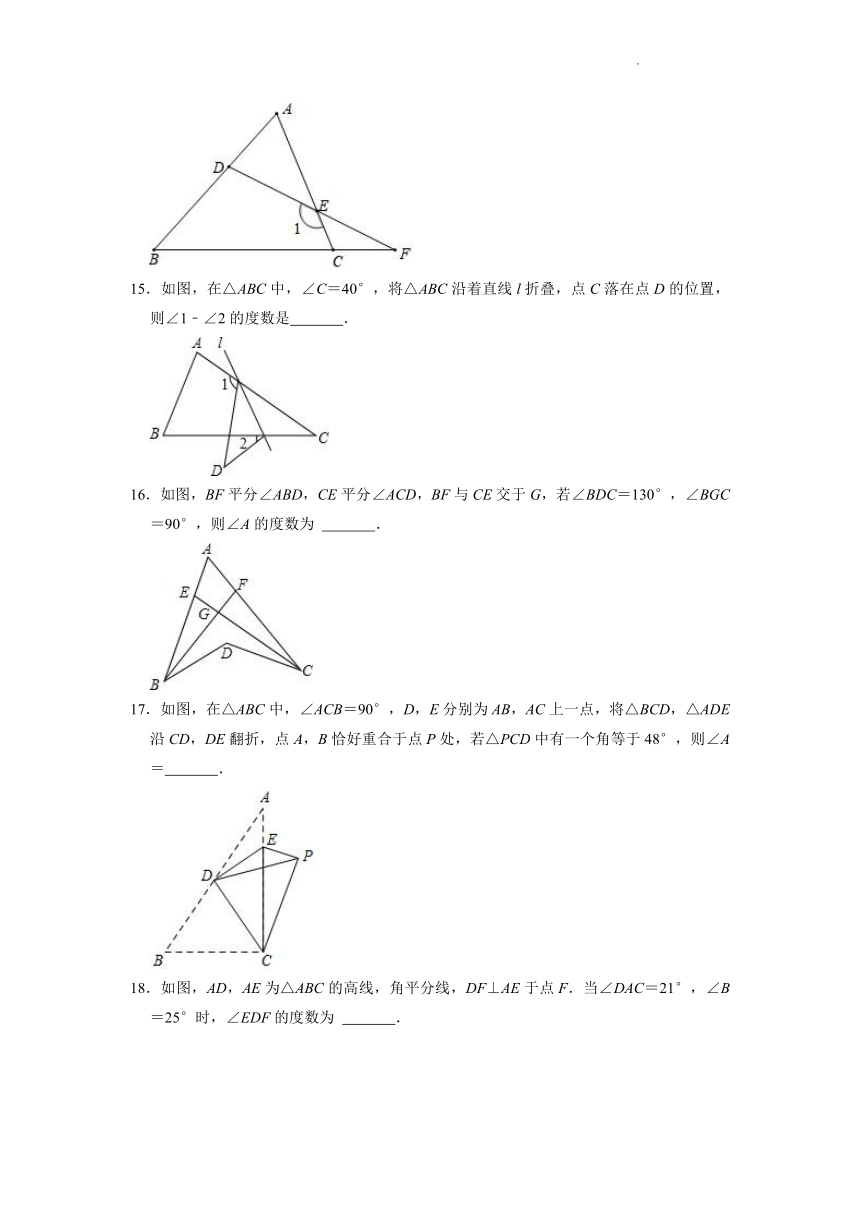
15.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是 .
16.如图,BF平分∠ABD,CE平分∠ACD,BF与CE交于G,若∠BDC=130°,∠BGC=90°,则∠A的度数为 .
17.如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE沿CD,DE翻折,点A,B恰好重合于点P处,若△PCD中有一个角等于48°,则∠A= .
18.如图,AD,AE为△ABC的高线,角平分线,DF⊥AE于点F.当∠DAC=21°,∠B=25°时,∠EDF的度数为 .
19.如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2…依次类推,则∠A4= 度.
三.解答题
20.如图,在△ABC中,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若△ABC的面积为40,BD=5,求AF的长;
(2)若∠BED=40°,∠BAD=25°,求∠BAF的大小.
21.∠MON=90°,点A,B分别在射线OM、ON上运动(不与点O重合).
(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB= °;
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
①若∠BAO=60°,则∠D= °;
②随着点A,B的运动,∠D的大小是否会变化?如果不变,求∠D的度数;如果变化,请说明理由.
22.在一个三角形中,如果一个角是另一个角的2倍,这样的三角形我们称之为“倍角三角形”.如三个内角分别为20°,40°,120°的三角形是“倍角三角形”.
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交射线OB于点C.
(1)△AOB (填“是”或“不是”)倍角三角形;
(2)若△AOC为“倍角三角形”,求∠OAC;
(3)若△ABC为“倍角三角形”,求∠ACB.
23.(1)如图1,在△ABC纸片中,点D在边AC上,点E在边AB上,沿DE折叠,当点A落在CD上时,∠DAE与∠1之间有一种数量关系保持不变,请找出这种数量关系并说明理由;
(2)若折成图2时,即点A落在△ABC内时,请找出∠DAE与∠1,∠2之间的关系式并说明理由.
24.如图所示,在△ABC中,∠ABC=60°,∠ACB=45°,AD,CF分别是BC,AB边上的高,且相交于点P,∠ABC的平分线BE分别交AD,CF于M,N.
(1)试找出图中所有的等腰三角形,请写出来;
(2)图中是否有等边三角形?若有,请找出并说明理由.
25.(1)已知:如图①的图形我们把它称为“8字形”,试说明:∠A+∠B=∠C+∠D.
(2)如图②,AP,CP分别平分∠BAD,∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 ;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 .
26.如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.
(1)猜想直线AB与直线CD有怎样的位置关系?说明你的理由;
(2)若点G为直线CD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①如图2,当点G在射线FD上运动时,若β=56°,求α的度数;
②当点G在直线CD上运动时,请直接写出α和β的数量关系.
参考答案
一.选择题
1.解:∵DF⊥AB(已知),
∴∠EFA=90°(垂直定义),
在△AEF中,∠EFA=90°,∠A=35°(已知),
∴∠AEF=180°﹣∠EFA﹣∠A=180°﹣90°﹣35°=55°,
又∵∠CED=∠AEF(对顶角相等),
∴∠CED=55°,
在△CDE中,∠CED=55°,∠ECD=85°(已知),
∴∠D=180°﹣∠CED﹣∠ECD=180°﹣55°﹣85°=40°.
故选:B.
2.解:∵∠A=α,∠DBC=3∠DBA,∠DCB=3∠DCA,
设∠ABD=β,∠ACD=θ,
∴∠DBC=3β,∠DCB=3θ,
∵∠A+∠ABC+∠ACB=180°,
∴α+4β+4θ=180°,
∴β+θ=45°﹣,
∴∠BDC=180°﹣3(β+θ)=180°﹣3×(45°﹣)=45,
故选:A.
3.解:∵∠C+∠A+∠B=180°,∠C=∠A+∠B,
∴∠A+∠B=90°.
∵∠B=2∠A﹣12°,
∴∠A+2∠A﹣12°=90°.
∴∠A=34°.
∴∠B=56°.
故选:C.
4.解:∵∠CAB=40°,∠B=50°,
∴∠ACB=180°﹣40°﹣50°=90°,
∵CE⊥AD,
∴∠AFC=∠AFE=90°,
∵AD是△ABC的角平分线,
∴∠CAD=∠EAD=×40°=20°,
又∵AF=AF,
∴△ACF≌△AEF(ASA)
∴AC=AE,
∵AD=AD,∠CAD=∠EAD,
∴△ACD≌△AED (SAS),
∴DC=DE,
∴∠DCE=∠DEC,
∵∠ACE=90°﹣20°=70°,
∴∠DCE=∠DEC=∠ACB﹣∠ACE=90°﹣70°=20°,
∴∠BDE=∠DCE+∠DEC=20°+20°=40°,
故选:B.
5.解:如图,设A′D与AD交于点O,
∵∠A=40°,
∴∠A′=∠A=40°,
∵∠1=∠DOA+∠A,∠1=112°,
∴∠DOA=∠1﹣∠A=112°﹣40°=72°,
∵∠DOA=∠2+∠A′,
∴∠2=∠DOA﹣∠A′=72°﹣40°=32°.
故选:A.
6.解:∵AC∥EF,
∴∠DBE=∠C=45°,
∴∠FBD=135°,
∵∠E=60°,∠EDF=90°,
∴∠F=30°,
∴∠FDC=∠F+∠FBD=30°+135°=165°,
故选:C.
7.解:设∠DAB=2x,∠DCB=2y,
∵AP平分∠DAB,CP平分∠DCB,
∴∠DAP=∠PAB==x,∠DCP=∠PCB=∠DCB=y,
∵∠D+∠DAP+∠AMD=180°,∠P+∠DCP+∠CMP=180°,
∵∠AMD=∠CMP,
∴∠D+∠DAP=∠P+∠DCP,
同理∠B+∠PCB=∠P+∠PAB,
∵∠D=50°,∠B=40°,
∴50°+x=∠P+y,40°+y=∠P+x,
相加得:50°+x+40°+y=∠P+x+∠P+y,
解得:∠P=45°,
故选:B.
8.解:∵∠BDC=90°,
∴∠DBC+∠DCB=180°﹣90°=90°,
∵∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°,
∴90°+(∠ABD+∠ACD)+∠A=180°,
∵∠DBA+∠DCA=n°,
∴∠A=90°﹣n°,
故选:C.
9.解:在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DE∥BC,
∴∠ACB=∠AED,
∵BG平分∠ABC,EF平分∠AED,
∴∠ABG=∠ABC,∠AEF=∠AED,
∴∠AEF=∠AED=∠ACB,
∵∠AGF是△EFG的一个外角,
∴∠AGB=∠F+∠AEF
=∠F+∠ACB,
在△ABG中,∠A+∠ABG+∠AGB=180°,
∴∠A+∠ABC+∠F+∠ACB=180°,
∠A+∠F+(∠ABC+∠ACB)=180°,
∠A+∠F+(180°﹣∠A)=180°,
整理得:∠A+∠F=90°,
∵3∠A=4∠F,
∴∠F=∠A,
∴∠A+∠A=90°,
解得:∠A=72°.
故选:C.
10.解:如图,
由题意得:△ABN≌△A′BN,△C′BN≌△CBM.
∴∠1=∠2,∠2=∠3,∠CMB=∠C′MB=68°.
∴∠1=∠2=∠3.
∴∠ABC=3∠3.
又∵∠3+∠C+∠CMB=180°,
∴∠3+∠C=180°﹣∠CMB=180°﹣68°=112°.
又∵∠A+∠ABC+∠C=180°,
∴18°+2∠3+(∠3+∠C)=180°.
∴18°+2∠3+112°=180°.
∴∠3=25°.
∴∠C=112°﹣∠3=112°﹣25°=87°.
故选:A.
11.解:∵∠CAB=90°,AD是∠CAB的角平分线,
∴∠CAD=∠BAD=∠CAB=45°,
∵CE⊥AD,
∴∠ECA=∠CEA﹣∠CAE=45°,
∵∠BCA=∠CAB﹣∠B=20°,
∴∠ECD=∠ACE﹣∠BCA=25°,
故选:C.
12.解:在△BEC中,
∵∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ABC、∠ACB的三等分线交于点E、D,
∴∠DBC=∠EBC,∠DCB=∠ECB,
∴∠DBC+∠DCB=×90°=45°,
∴∠BDC=180°﹣(∠DBC+∠DCB)=135°,
故选:D.
二.填空题
13.解:∵∠A+∠ACB+∠ABC=180°,∠A=90°,
∴∠ACB+∠ABC=90°,
∵∠GCF=∠ACB,∠DBE=∠ABC,
∴∠GCF+∠DBE=90°,
∵∠G+∠F+∠GCF=∠D+∠B+∠DBE=180°,
∴∠G+∠F+∠GCF+∠D+∠B+∠DBE=360°,
∴∠D+∠G+∠AFG+∠AED=270°,
故答案为:270°.
14.解:∵∠B=50°,∠F=35°,
∴∠ADE=∠B+∠F=85°,
∵∠A=60°,
∴∠1=∠A+∠ADE=60°+85°=145°,
故答案为:145°.
15.解:如图,
由折叠的性质得:∠D=∠C=40°,
根据外角性质得:∠1=∠3+∠C,∠3=∠2+∠D,
则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+80°,
则∠1﹣∠2=80°.
故答案为80°.
16.解:连接BC,如图,
∵∠BDC=130°,
∴∠DBC+∠DCB=180°﹣130°=50°,
∵∠BGC=90°,
∴∠GBC+∠GCB=180°﹣90°=90°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=∠ABD+∠ACD=40°,
∴∠ABC+∠ACB=130°,
∴∠A=180°﹣130°=50°.
故答案为:50°.
17.解:由折叠可得,AD=PD=BD,∠CPD=∠B,∠PDC=∠BDC,∠PCD=∠DCB,
∴D是AB的中点
∴CD=AB=AD=BD,
∴∠ACD=∠A,∠DCB=∠B,
当∠CPD=48°时,∠B=48°,
∴∠A=90°﹣∠B=42°;
当∠PCD=48°时,∠DCB=∠B=48°,
∴∠A=42°;
当∠PDC=48°时,
∵∠PCD=DCB=48°,∠BDC=∠A+∠ACD,
∴∠A=∠BDC=24°;
故答案为:42°或24°.
18.解:∵AD,AE为△ABC的高线,角平分线,
∴∠EAB=∠BAC,∠ADC=90°.
∵∠DAC=21°,∠B=25°,
∴∠C=90°﹣∠DAC
=69°,
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣25°﹣69°
=86°.
∴∠BAE=43°.
∴∠AED=∠BAE+∠B
=43°+25°
=68°.
∵DF⊥AE,
∴∠EFD=90°.
∴∠EDF=90°﹣∠DEA
=90°﹣68°
=22°.
故答案为:22°.
19.解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
同理可得∠A2=∠A1=×∠A=∠A,
由此可得一下规律:∠An=∠A,
当∠A=64°时,∠A4=∠A=4°,
故答案为:4.
三.解答题
20.解:(1)∵AD是△ABC的中线,BD=5,
∴BC=2BD=2×5=10,
∵AF⊥BC,S△ABC=40,
∴,
∴AF=8;
(2)在△ABE中,∠BED为它的一个外角,且∠BED=40°,∠BAD=25°,
∴∠ABE=∠BED﹣∠BAD=40°﹣25°=15°,
∵BE是△ABD的角平分线,
∴∠ABC=2∠ABE=2×15°=30°,
∵AF⊥BC,
∴∠AFB=90°,
在Rt△ABF中,∠BAF=90°﹣∠ABC=90°﹣30°=60°.
21.解:(1)∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
故答案为:135;
(2)①∵∠AOB=90°,∠BAO=60°,
∴∠ABO=30°,
∴∠ABN=150°,
∵BC是∠ABN的平分线,
∴∠OBD=∠CBN=150°=75°,
∵AD平分∠BAO,
∴∠DAB=30°,
∴∠D=180°﹣∠ABD﹣∠BAD﹣∠AOB=180°﹣75°﹣30°﹣30°=45°,
故答案为:45;
②∠D的度数不随A、B的移动而发生变化,
设∠BAD=α,
∵AD平分∠BAO,
∴∠BAO=2α,
∵∠AOB=90°,
∴∠ABN=180°﹣∠ABO=∠AOB+∠BAO=90+2α,
∵BC平分∠ABN,
∴∠ABC=45°+α,
∵∠ABC=180°﹣∠ABD=∠D+∠BAD,
∴∠D=∠ABC﹣∠BAD=45°+α﹣α=45°.
22.解:(1)∵AB⊥OM,∠MON=60°,
∴∠ABO=30°,
∴∠AOB=2∠ABO,
∴△AOB 是“倍角三角形”,
故答案为:是;
(2)∵∠AOC=60°,△AOC为“倍角三角形”,
∴当∠AOC=2∠OAC时,∠OAC=30°,
当∠AOC=2∠ACO时,∠OAC=90°,
当∠ACO=2∠OAC时,∠OAC=40°,
当∠OAC=2∠ACO时,∠OAC=80°,
综上所述,∠OAC为30°、90°、40°或80°;
(3)∵∠ABC=30°,△ABC为“倍角三角形”,
∴当点C在线段OB上时,有4种情况:
①∠ACB=2∠ABC,这时∠ACB=60°,
②∠ABC=2∠BAC,这时∠ACB=135°,
③∠BAC=2∠ABC,这时∠ACB=90°,
④∠ACB=2∠BAC,这时∠ACB=100°,
当点C在射线BN上时,有2种情况:
①∠BAC=2∠ACB,这时∠ACB=10°,
②∠ACB=2∠BAC,这时∠ACB=20°,
综上所述,∠ACB为60°、135°、90°、100°、10°或20°.
23.解:(1)结论:∠1=2∠DAE.
理由:如图1中,延长BE交CD于R.
由翻折可知,∠EAD=∠R,
∵∠1=∠EAD+∠R,
∴∠1=2∠EAD.
(2)结论:∠1+∠2=2∠EAD.
理由:如图2中,延长BE交CD的延长线于T,连接AT.
由翻折可知,∠EAD=∠ETD,
∵∠1=∠EAT+∠ETA,∠2=∠DAT+∠DTA,
∴∠1+∠2=∠EAT+∠ETA+∠DAT+∠DTA=∠EAD+∠ETD=2∠EAD.
24.解:(1)∵∠ABC=60°,∠ACB=45°,AD、CF都是高,
∴∠DAC=45°,
∴CD=AD,
∴△ADC为等腰直角三角形,
∴∠BAD=30°,
∴∠APF=60°,
∵∠ABC=60°BE是∠ABC的角平分线,
∴∠MBD=30°,
∴∠BMD=60°,
∴NP=NM,
∴△MNP为等腰三角形;
∵∠ABC=60°,BE是∠ABC平分线,∴∠ABE=∠CBE=30°,
在△ABD中,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣60°﹣90°=30°,
∴∠ABM=∠BAD=30°,
∴AM=BM即△ABM是等腰三角形,
在△BFC中,∠BCF=180°﹣∠ABC﹣∠BFC=180°﹣60°﹣90°=30°,
∴∠CBE=∠BCF=30°,
∴BN=CN即△BCN是等腰三角形,
在△ABC中,∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣45°=75°,
∵∠AEB=∠CBE+∠ACB=30°+45°=75°,
∴∠BAE=∠BEA,
∴AB=EB即△ABE是等腰三角形,
在△ACD中,∠CAD=180°﹣∠ADC﹣∠BCA=180°﹣90°﹣45°=45°,
∴∠CAD=∠BCA=45°,
∴AD=CD即△ACD是等腰三角形,
∴等腰三角形有△ACD,△ABM,△ABE,△BCN,△MNP;
(2)由∠BMD=60°,
∴△MNP为等边三角形.
25.解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)∵AP,CP分别平分∠BAD,∠BCD,
∴∠BAP=∠PAD,∠BCP=∠PCD,
由(1)的结论得,∠P+∠BCP=∠ABC+∠BAP,①,
∠P+∠PAD=∠ADC+∠PCD②,
①+②得,2∠P+∠BCP+∠PAD=∠BAP+∠PCD+∠ABC+∠ADC,
∴2∠P=∠ABC+∠ADC,
∵∠ABC=36°,∠ADC=16°,
∴∠P=26°.
(3)∵直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠PAB=∠PAD,∠PCB=∠PCE,
∴2∠PAB+∠B=180°﹣2∠PCB+∠D,
∴180°﹣2(∠PAB+∠PCB)+∠D=∠B,
∵∠P+∠PAD=∠PCB+∠AOC=∠PCB+∠B+2∠PAD,
∴∠P=∠PAD+∠B+∠PCB=∠PAB+∠B+∠PCB,
∴∠PAB+∠PCB=∠P﹣∠B,
∴180°﹣2(∠P﹣∠B)+∠D=∠B,即∠P=90°+(∠B+∠D).
故答案为:∠P=90°+(∠B+∠D).
(4)∵直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠FAP=∠PAO,∠PCE=∠PCB,
在四边形APCB中,(180°﹣∠FAP)+∠P+∠PCB+∠B=360°①,
在四边形APCD中,∠PAD+∠P+(180°﹣∠PCE)+∠D=360°②,
①+②得:2∠P+∠B+∠D=360°,
∴∠P=180°﹣(∠B+∠D).
故答案为:∠P=180°﹣(∠B+∠D).
26.解:(1)结论:AB∥CD.
理由:如图1中,
∵EM平分∠AEF交CD于点M,
∴∠AEM=∠MEF,
∵∠FEM=∠FME.
∴∠AEM=∠FME,
∴AB∥CD.
(2)①如图2中,
∵AB∥CD,
∴∠BEG=∠EGF=β=56°,
∴∠AEG=124°,
∵∠AEM=∠MEF,∠HEF=∠HEG,
∴∠HEN=∠MEF+∠HEF=∠AEG=62°,
∵HN⊥EM,
∴∠HNE=90°,
∴α=∠EHN=90°﹣∠HEN=28°.
②结论:α=β或α=90°﹣β.
理由:当点G在F的右侧时,可得α=β.
∵AB∥CD,
∴∠BEG=∠EGF=β,
∴∠AEG=180°﹣β,
∵∠AEM=∠MEF,∠HEF=∠HEG,
∴∠HEN=∠MEF+∠HEF=∠AEG=90°﹣β,
∵HN⊥EM,
∴∠HNE=90°,
∴α=∠EHN=90°﹣∠HEN=β.
当点G在FM上时,可得α=90°﹣β.
理由:∵AB∥CD,
∴∠AEG=∠EGF=β,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠MEF﹣∠HEF
=(∠AEF﹣∠FEG)
=∠AEG
=β,
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°﹣∠MEH,
即α=90°﹣β;
当点G在点M的左侧时,可得α=90°﹣β.
理由:∵AB∥CD,
∴∠AEG=∠EGF=β,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠MEF﹣∠HEF
=(∠AEF﹣∠FEG)
=∠AEG
=β,
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°﹣∠MEH,
即α=90°﹣β.
一.选择题
1.如图,在△ABC中,D在BC的延长线上,过D作DF⊥AB于F,交AC于E.已知∠A=35°,∠ECD=85°,则∠D=( )
A.30° B.40° C.45° D.50°
2.如图,∠A=α,∠DBC=3∠DBA,∠DCB=3∠DCA,则∠BDC的大小为( )
A. B. C. D.
3.在△ABC中,∠C=∠A+∠B,∠B=2∠A﹣12°,则∠B的度数为( )
A.78° B.58° C.56° D.34°
4.如图,AD是△ABC的角平分线,CE⊥AD,垂足为F.若∠CAB=40°,∠B=50°,则∠BDE的度数为( )
A.35° B.40° C.45° D.50°
5.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外面时,此时测得∠1=112°,∠A=40°,则∠2的度数为( )
A.32° B.33° C.34° D.38°
6.将一副三角板如图放置,∠FDE=∠A=90°,∠C=45°,∠E=60°,且点D在BC上,点B在EF上,AC∥EF,则∠FDC的度数为( )
A.150° B.160° C.165° D.155°
7.如图,已知AB,CD是两条相交线段,连结AD,CB,分别作∠DAB和∠BCD的平分线相交于点P,若∠D=50°,∠B=40°,则∠P的度数为( )
A.50° B.45° C.40° D.30°
8.有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C,在△ABC中,∠DBA+∠DCA=n°,则∠A的度数是( )
A.90°+n° B.45°+n° C.90°﹣n° D.180°﹣n°
9.如图,延长△ABC的边AC到点E,过点E作DE∥BC,BG平分∠ABC,EF平分∠AED交BG的反向延长找于点F.已知3∠A=4∠F,则∠A的大小为( )
A.75° B.74° C.72° D.70°
10.如图,小明从一张三角形纸片ABC的AC边上选取一点N,将纸片沿着BN对折一次使得点A落在A′处后,再将纸片沿着BA′对折一次,使得点C落在BN上的C′处,已知∠CMB=68°,∠A=18°,则原三角形的∠C的度数为( )
A.87° B.84° C.75° D.72°
11.如图,在直角△ABC中,∠CAB=90°,∠ABC=70°,AD是∠CAB的平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( )
A.35° B.30° C.25° D.20°
12.如图,△ABC中,∠ABC、∠ACB的三等分线交于点E、D,若∠E=90°,则∠BDC的度数为( )
A.120° B.125° C.130° D.135°
二.填空题
13.如图,线段AF⊥AE,垂足为点A,线段GD分别交AF、AE于点C,B,连结GF,ED.则∠D+∠G+∠AFG+∠AED的度数为 .
14.如图,△ABC中,∠A=60°,∠B=50°,D、E分别是AB、AC上两点,连接DE并延长,交BC的延长线于点F,此时,∠F=35°,则∠1的度数为 .
15.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是 .
16.如图,BF平分∠ABD,CE平分∠ACD,BF与CE交于G,若∠BDC=130°,∠BGC=90°,则∠A的度数为 .
17.如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE沿CD,DE翻折,点A,B恰好重合于点P处,若△PCD中有一个角等于48°,则∠A= .
18.如图,AD,AE为△ABC的高线,角平分线,DF⊥AE于点F.当∠DAC=21°,∠B=25°时,∠EDF的度数为 .
19.如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2…依次类推,则∠A4= 度.
三.解答题
20.如图,在△ABC中,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若△ABC的面积为40,BD=5,求AF的长;
(2)若∠BED=40°,∠BAD=25°,求∠BAF的大小.
21.∠MON=90°,点A,B分别在射线OM、ON上运动(不与点O重合).
(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB= °;
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
①若∠BAO=60°,则∠D= °;
②随着点A,B的运动,∠D的大小是否会变化?如果不变,求∠D的度数;如果变化,请说明理由.
22.在一个三角形中,如果一个角是另一个角的2倍,这样的三角形我们称之为“倍角三角形”.如三个内角分别为20°,40°,120°的三角形是“倍角三角形”.
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交射线OB于点C.
(1)△AOB (填“是”或“不是”)倍角三角形;
(2)若△AOC为“倍角三角形”,求∠OAC;
(3)若△ABC为“倍角三角形”,求∠ACB.
23.(1)如图1,在△ABC纸片中,点D在边AC上,点E在边AB上,沿DE折叠,当点A落在CD上时,∠DAE与∠1之间有一种数量关系保持不变,请找出这种数量关系并说明理由;
(2)若折成图2时,即点A落在△ABC内时,请找出∠DAE与∠1,∠2之间的关系式并说明理由.
24.如图所示,在△ABC中,∠ABC=60°,∠ACB=45°,AD,CF分别是BC,AB边上的高,且相交于点P,∠ABC的平分线BE分别交AD,CF于M,N.
(1)试找出图中所有的等腰三角形,请写出来;
(2)图中是否有等边三角形?若有,请找出并说明理由.
25.(1)已知:如图①的图形我们把它称为“8字形”,试说明:∠A+∠B=∠C+∠D.
(2)如图②,AP,CP分别平分∠BAD,∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 ;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 .
26.如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.
(1)猜想直线AB与直线CD有怎样的位置关系?说明你的理由;
(2)若点G为直线CD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①如图2,当点G在射线FD上运动时,若β=56°,求α的度数;
②当点G在直线CD上运动时,请直接写出α和β的数量关系.
参考答案
一.选择题
1.解:∵DF⊥AB(已知),
∴∠EFA=90°(垂直定义),
在△AEF中,∠EFA=90°,∠A=35°(已知),
∴∠AEF=180°﹣∠EFA﹣∠A=180°﹣90°﹣35°=55°,
又∵∠CED=∠AEF(对顶角相等),
∴∠CED=55°,
在△CDE中,∠CED=55°,∠ECD=85°(已知),
∴∠D=180°﹣∠CED﹣∠ECD=180°﹣55°﹣85°=40°.
故选:B.
2.解:∵∠A=α,∠DBC=3∠DBA,∠DCB=3∠DCA,
设∠ABD=β,∠ACD=θ,
∴∠DBC=3β,∠DCB=3θ,
∵∠A+∠ABC+∠ACB=180°,
∴α+4β+4θ=180°,
∴β+θ=45°﹣,
∴∠BDC=180°﹣3(β+θ)=180°﹣3×(45°﹣)=45,
故选:A.
3.解:∵∠C+∠A+∠B=180°,∠C=∠A+∠B,
∴∠A+∠B=90°.
∵∠B=2∠A﹣12°,
∴∠A+2∠A﹣12°=90°.
∴∠A=34°.
∴∠B=56°.
故选:C.
4.解:∵∠CAB=40°,∠B=50°,
∴∠ACB=180°﹣40°﹣50°=90°,
∵CE⊥AD,
∴∠AFC=∠AFE=90°,
∵AD是△ABC的角平分线,
∴∠CAD=∠EAD=×40°=20°,
又∵AF=AF,
∴△ACF≌△AEF(ASA)
∴AC=AE,
∵AD=AD,∠CAD=∠EAD,
∴△ACD≌△AED (SAS),
∴DC=DE,
∴∠DCE=∠DEC,
∵∠ACE=90°﹣20°=70°,
∴∠DCE=∠DEC=∠ACB﹣∠ACE=90°﹣70°=20°,
∴∠BDE=∠DCE+∠DEC=20°+20°=40°,
故选:B.
5.解:如图,设A′D与AD交于点O,
∵∠A=40°,
∴∠A′=∠A=40°,
∵∠1=∠DOA+∠A,∠1=112°,
∴∠DOA=∠1﹣∠A=112°﹣40°=72°,
∵∠DOA=∠2+∠A′,
∴∠2=∠DOA﹣∠A′=72°﹣40°=32°.
故选:A.
6.解:∵AC∥EF,
∴∠DBE=∠C=45°,
∴∠FBD=135°,
∵∠E=60°,∠EDF=90°,
∴∠F=30°,
∴∠FDC=∠F+∠FBD=30°+135°=165°,
故选:C.
7.解:设∠DAB=2x,∠DCB=2y,
∵AP平分∠DAB,CP平分∠DCB,
∴∠DAP=∠PAB==x,∠DCP=∠PCB=∠DCB=y,
∵∠D+∠DAP+∠AMD=180°,∠P+∠DCP+∠CMP=180°,
∵∠AMD=∠CMP,
∴∠D+∠DAP=∠P+∠DCP,
同理∠B+∠PCB=∠P+∠PAB,
∵∠D=50°,∠B=40°,
∴50°+x=∠P+y,40°+y=∠P+x,
相加得:50°+x+40°+y=∠P+x+∠P+y,
解得:∠P=45°,
故选:B.
8.解:∵∠BDC=90°,
∴∠DBC+∠DCB=180°﹣90°=90°,
∵∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°,
∴90°+(∠ABD+∠ACD)+∠A=180°,
∵∠DBA+∠DCA=n°,
∴∠A=90°﹣n°,
故选:C.
9.解:在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DE∥BC,
∴∠ACB=∠AED,
∵BG平分∠ABC,EF平分∠AED,
∴∠ABG=∠ABC,∠AEF=∠AED,
∴∠AEF=∠AED=∠ACB,
∵∠AGF是△EFG的一个外角,
∴∠AGB=∠F+∠AEF
=∠F+∠ACB,
在△ABG中,∠A+∠ABG+∠AGB=180°,
∴∠A+∠ABC+∠F+∠ACB=180°,
∠A+∠F+(∠ABC+∠ACB)=180°,
∠A+∠F+(180°﹣∠A)=180°,
整理得:∠A+∠F=90°,
∵3∠A=4∠F,
∴∠F=∠A,
∴∠A+∠A=90°,
解得:∠A=72°.
故选:C.
10.解:如图,
由题意得:△ABN≌△A′BN,△C′BN≌△CBM.
∴∠1=∠2,∠2=∠3,∠CMB=∠C′MB=68°.
∴∠1=∠2=∠3.
∴∠ABC=3∠3.
又∵∠3+∠C+∠CMB=180°,
∴∠3+∠C=180°﹣∠CMB=180°﹣68°=112°.
又∵∠A+∠ABC+∠C=180°,
∴18°+2∠3+(∠3+∠C)=180°.
∴18°+2∠3+112°=180°.
∴∠3=25°.
∴∠C=112°﹣∠3=112°﹣25°=87°.
故选:A.
11.解:∵∠CAB=90°,AD是∠CAB的角平分线,
∴∠CAD=∠BAD=∠CAB=45°,
∵CE⊥AD,
∴∠ECA=∠CEA﹣∠CAE=45°,
∵∠BCA=∠CAB﹣∠B=20°,
∴∠ECD=∠ACE﹣∠BCA=25°,
故选:C.
12.解:在△BEC中,
∵∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ABC、∠ACB的三等分线交于点E、D,
∴∠DBC=∠EBC,∠DCB=∠ECB,
∴∠DBC+∠DCB=×90°=45°,
∴∠BDC=180°﹣(∠DBC+∠DCB)=135°,
故选:D.
二.填空题
13.解:∵∠A+∠ACB+∠ABC=180°,∠A=90°,
∴∠ACB+∠ABC=90°,
∵∠GCF=∠ACB,∠DBE=∠ABC,
∴∠GCF+∠DBE=90°,
∵∠G+∠F+∠GCF=∠D+∠B+∠DBE=180°,
∴∠G+∠F+∠GCF+∠D+∠B+∠DBE=360°,
∴∠D+∠G+∠AFG+∠AED=270°,
故答案为:270°.
14.解:∵∠B=50°,∠F=35°,
∴∠ADE=∠B+∠F=85°,
∵∠A=60°,
∴∠1=∠A+∠ADE=60°+85°=145°,
故答案为:145°.
15.解:如图,
由折叠的性质得:∠D=∠C=40°,
根据外角性质得:∠1=∠3+∠C,∠3=∠2+∠D,
则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+80°,
则∠1﹣∠2=80°.
故答案为80°.
16.解:连接BC,如图,
∵∠BDC=130°,
∴∠DBC+∠DCB=180°﹣130°=50°,
∵∠BGC=90°,
∴∠GBC+∠GCB=180°﹣90°=90°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=∠ABD+∠ACD=40°,
∴∠ABC+∠ACB=130°,
∴∠A=180°﹣130°=50°.
故答案为:50°.
17.解:由折叠可得,AD=PD=BD,∠CPD=∠B,∠PDC=∠BDC,∠PCD=∠DCB,
∴D是AB的中点
∴CD=AB=AD=BD,
∴∠ACD=∠A,∠DCB=∠B,
当∠CPD=48°时,∠B=48°,
∴∠A=90°﹣∠B=42°;
当∠PCD=48°时,∠DCB=∠B=48°,
∴∠A=42°;
当∠PDC=48°时,
∵∠PCD=DCB=48°,∠BDC=∠A+∠ACD,
∴∠A=∠BDC=24°;
故答案为:42°或24°.
18.解:∵AD,AE为△ABC的高线,角平分线,
∴∠EAB=∠BAC,∠ADC=90°.
∵∠DAC=21°,∠B=25°,
∴∠C=90°﹣∠DAC
=69°,
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣25°﹣69°
=86°.
∴∠BAE=43°.
∴∠AED=∠BAE+∠B
=43°+25°
=68°.
∵DF⊥AE,
∴∠EFD=90°.
∴∠EDF=90°﹣∠DEA
=90°﹣68°
=22°.
故答案为:22°.
19.解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
同理可得∠A2=∠A1=×∠A=∠A,
由此可得一下规律:∠An=∠A,
当∠A=64°时,∠A4=∠A=4°,
故答案为:4.
三.解答题
20.解:(1)∵AD是△ABC的中线,BD=5,
∴BC=2BD=2×5=10,
∵AF⊥BC,S△ABC=40,
∴,
∴AF=8;
(2)在△ABE中,∠BED为它的一个外角,且∠BED=40°,∠BAD=25°,
∴∠ABE=∠BED﹣∠BAD=40°﹣25°=15°,
∵BE是△ABD的角平分线,
∴∠ABC=2∠ABE=2×15°=30°,
∵AF⊥BC,
∴∠AFB=90°,
在Rt△ABF中,∠BAF=90°﹣∠ABC=90°﹣30°=60°.
21.解:(1)∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
故答案为:135;
(2)①∵∠AOB=90°,∠BAO=60°,
∴∠ABO=30°,
∴∠ABN=150°,
∵BC是∠ABN的平分线,
∴∠OBD=∠CBN=150°=75°,
∵AD平分∠BAO,
∴∠DAB=30°,
∴∠D=180°﹣∠ABD﹣∠BAD﹣∠AOB=180°﹣75°﹣30°﹣30°=45°,
故答案为:45;
②∠D的度数不随A、B的移动而发生变化,
设∠BAD=α,
∵AD平分∠BAO,
∴∠BAO=2α,
∵∠AOB=90°,
∴∠ABN=180°﹣∠ABO=∠AOB+∠BAO=90+2α,
∵BC平分∠ABN,
∴∠ABC=45°+α,
∵∠ABC=180°﹣∠ABD=∠D+∠BAD,
∴∠D=∠ABC﹣∠BAD=45°+α﹣α=45°.
22.解:(1)∵AB⊥OM,∠MON=60°,
∴∠ABO=30°,
∴∠AOB=2∠ABO,
∴△AOB 是“倍角三角形”,
故答案为:是;
(2)∵∠AOC=60°,△AOC为“倍角三角形”,
∴当∠AOC=2∠OAC时,∠OAC=30°,
当∠AOC=2∠ACO时,∠OAC=90°,
当∠ACO=2∠OAC时,∠OAC=40°,
当∠OAC=2∠ACO时,∠OAC=80°,
综上所述,∠OAC为30°、90°、40°或80°;
(3)∵∠ABC=30°,△ABC为“倍角三角形”,
∴当点C在线段OB上时,有4种情况:
①∠ACB=2∠ABC,这时∠ACB=60°,
②∠ABC=2∠BAC,这时∠ACB=135°,
③∠BAC=2∠ABC,这时∠ACB=90°,
④∠ACB=2∠BAC,这时∠ACB=100°,
当点C在射线BN上时,有2种情况:
①∠BAC=2∠ACB,这时∠ACB=10°,
②∠ACB=2∠BAC,这时∠ACB=20°,
综上所述,∠ACB为60°、135°、90°、100°、10°或20°.
23.解:(1)结论:∠1=2∠DAE.
理由:如图1中,延长BE交CD于R.
由翻折可知,∠EAD=∠R,
∵∠1=∠EAD+∠R,
∴∠1=2∠EAD.
(2)结论:∠1+∠2=2∠EAD.
理由:如图2中,延长BE交CD的延长线于T,连接AT.
由翻折可知,∠EAD=∠ETD,
∵∠1=∠EAT+∠ETA,∠2=∠DAT+∠DTA,
∴∠1+∠2=∠EAT+∠ETA+∠DAT+∠DTA=∠EAD+∠ETD=2∠EAD.
24.解:(1)∵∠ABC=60°,∠ACB=45°,AD、CF都是高,
∴∠DAC=45°,
∴CD=AD,
∴△ADC为等腰直角三角形,
∴∠BAD=30°,
∴∠APF=60°,
∵∠ABC=60°BE是∠ABC的角平分线,
∴∠MBD=30°,
∴∠BMD=60°,
∴NP=NM,
∴△MNP为等腰三角形;
∵∠ABC=60°,BE是∠ABC平分线,∴∠ABE=∠CBE=30°,
在△ABD中,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣60°﹣90°=30°,
∴∠ABM=∠BAD=30°,
∴AM=BM即△ABM是等腰三角形,
在△BFC中,∠BCF=180°﹣∠ABC﹣∠BFC=180°﹣60°﹣90°=30°,
∴∠CBE=∠BCF=30°,
∴BN=CN即△BCN是等腰三角形,
在△ABC中,∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣45°=75°,
∵∠AEB=∠CBE+∠ACB=30°+45°=75°,
∴∠BAE=∠BEA,
∴AB=EB即△ABE是等腰三角形,
在△ACD中,∠CAD=180°﹣∠ADC﹣∠BCA=180°﹣90°﹣45°=45°,
∴∠CAD=∠BCA=45°,
∴AD=CD即△ACD是等腰三角形,
∴等腰三角形有△ACD,△ABM,△ABE,△BCN,△MNP;
(2)由∠BMD=60°,
∴△MNP为等边三角形.
25.解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)∵AP,CP分别平分∠BAD,∠BCD,
∴∠BAP=∠PAD,∠BCP=∠PCD,
由(1)的结论得,∠P+∠BCP=∠ABC+∠BAP,①,
∠P+∠PAD=∠ADC+∠PCD②,
①+②得,2∠P+∠BCP+∠PAD=∠BAP+∠PCD+∠ABC+∠ADC,
∴2∠P=∠ABC+∠ADC,
∵∠ABC=36°,∠ADC=16°,
∴∠P=26°.
(3)∵直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠PAB=∠PAD,∠PCB=∠PCE,
∴2∠PAB+∠B=180°﹣2∠PCB+∠D,
∴180°﹣2(∠PAB+∠PCB)+∠D=∠B,
∵∠P+∠PAD=∠PCB+∠AOC=∠PCB+∠B+2∠PAD,
∴∠P=∠PAD+∠B+∠PCB=∠PAB+∠B+∠PCB,
∴∠PAB+∠PCB=∠P﹣∠B,
∴180°﹣2(∠P﹣∠B)+∠D=∠B,即∠P=90°+(∠B+∠D).
故答案为:∠P=90°+(∠B+∠D).
(4)∵直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠FAP=∠PAO,∠PCE=∠PCB,
在四边形APCB中,(180°﹣∠FAP)+∠P+∠PCB+∠B=360°①,
在四边形APCD中,∠PAD+∠P+(180°﹣∠PCE)+∠D=360°②,
①+②得:2∠P+∠B+∠D=360°,
∴∠P=180°﹣(∠B+∠D).
故答案为:∠P=180°﹣(∠B+∠D).
26.解:(1)结论:AB∥CD.
理由:如图1中,
∵EM平分∠AEF交CD于点M,
∴∠AEM=∠MEF,
∵∠FEM=∠FME.
∴∠AEM=∠FME,
∴AB∥CD.
(2)①如图2中,
∵AB∥CD,
∴∠BEG=∠EGF=β=56°,
∴∠AEG=124°,
∵∠AEM=∠MEF,∠HEF=∠HEG,
∴∠HEN=∠MEF+∠HEF=∠AEG=62°,
∵HN⊥EM,
∴∠HNE=90°,
∴α=∠EHN=90°﹣∠HEN=28°.
②结论:α=β或α=90°﹣β.
理由:当点G在F的右侧时,可得α=β.
∵AB∥CD,
∴∠BEG=∠EGF=β,
∴∠AEG=180°﹣β,
∵∠AEM=∠MEF,∠HEF=∠HEG,
∴∠HEN=∠MEF+∠HEF=∠AEG=90°﹣β,
∵HN⊥EM,
∴∠HNE=90°,
∴α=∠EHN=90°﹣∠HEN=β.
当点G在FM上时,可得α=90°﹣β.
理由:∵AB∥CD,
∴∠AEG=∠EGF=β,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠MEF﹣∠HEF
=(∠AEF﹣∠FEG)
=∠AEG
=β,
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°﹣∠MEH,
即α=90°﹣β;
当点G在点M的左侧时,可得α=90°﹣β.
理由:∵AB∥CD,
∴∠AEG=∠EGF=β,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠MEF﹣∠HEF
=(∠AEF﹣∠FEG)
=∠AEG
=β,
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°﹣∠MEH,
即α=90°﹣β.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
