北京课改版物理八年级全一册课时同步作业:第五章 简单机械 章末复习(有答案)
文档属性
| 名称 | 北京课改版物理八年级全一册课时同步作业:第五章 简单机械 章末复习(有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 411.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-30 22:58:11 | ||
图片预览



文档简介
章末复习
核心要点突破
一、杠杆
1.定义:我们把绕固定点 的棒、杆或硬件等叫作杠杆。
2.五要素
(1)支点:杠杆 的固定点,如图中O点。
(2)动力: 杠杆转动的力,如图中F1。
(3)阻力: 杠杆转动的力,如图中F2。
(4)动力臂:从 到 的距离,如图中L1。
(5)阻力臂:从 到 的距离,如图中L2。
3.平衡条件
(1)文字表达式: 。
(2)字母表达式: 。
4.三种杠杆的分类
名称 特征 特点 应用举例
省力 杠杆 动力臂 阻力臂 省力、 距离 撬杠、铡刀、动滑轮、羊角锤、钢丝钳、手推车、花枝剪刀等
费力 杠杆 动力臂 阻力臂 力、省距离 缝纫机踏板、钓鱼竿、人的前臂、理发剪刀等
等臂 杠杆 动力臂 阻力臂 不省力、不费力 托盘天平、定滑轮等
二、轮轴
1.定义:由轮和轴组成,能绕共同轴线 的简单机械叫作轮轴。
2.工作特点:动力作用在轮上是 杠杆;动力作用在轴上是 杠杆。(均选填“省力”或“费力”)
3.生活中常见的轮轴类机械有 和 等。
三、滑轮
1.定滑轮的特点:可以 ,但不能 ;即F G, s h。定滑轮实质是一个 杠杆。
2.动滑轮的特点:可以 ,但不能 ;即F= G, s= h(在忽略滑轮重、绳重和摩擦的情况下)。动滑轮实质是一个 。
3.滑轮组的特点:既可以 ,又可以 。
关系:在忽略绳重、滑轮重和摩擦的情况下,动滑轮上有几段绳子承担物重,所用拉力就是物重的 ,即 ;绳端移动的距离就是物体上升高度的几倍,即 。
教材知识纵横
定滑轮、动滑轮、滑轮组的区别与联系
名称 定义 实质 特点 图示
轴固定不动的滑轮 等臂 杠杆 不省力,但可以改变用力的方向
轴跟物体一起运动的滑轮 动力臂为阻力臂二倍的杠 杆 能省一半的力,但不能改变用力的方向
由定滑轮和动滑轮组合而成 ①在忽略摩擦和绳重的情况下,使用滑轮组时,重物和动滑轮总重由几段绳子承担,提起重物所用的力就等于总重的几分之一,即F=; ②既可以省力,又可以改变用力的方向
命题点1 杠杆的分类
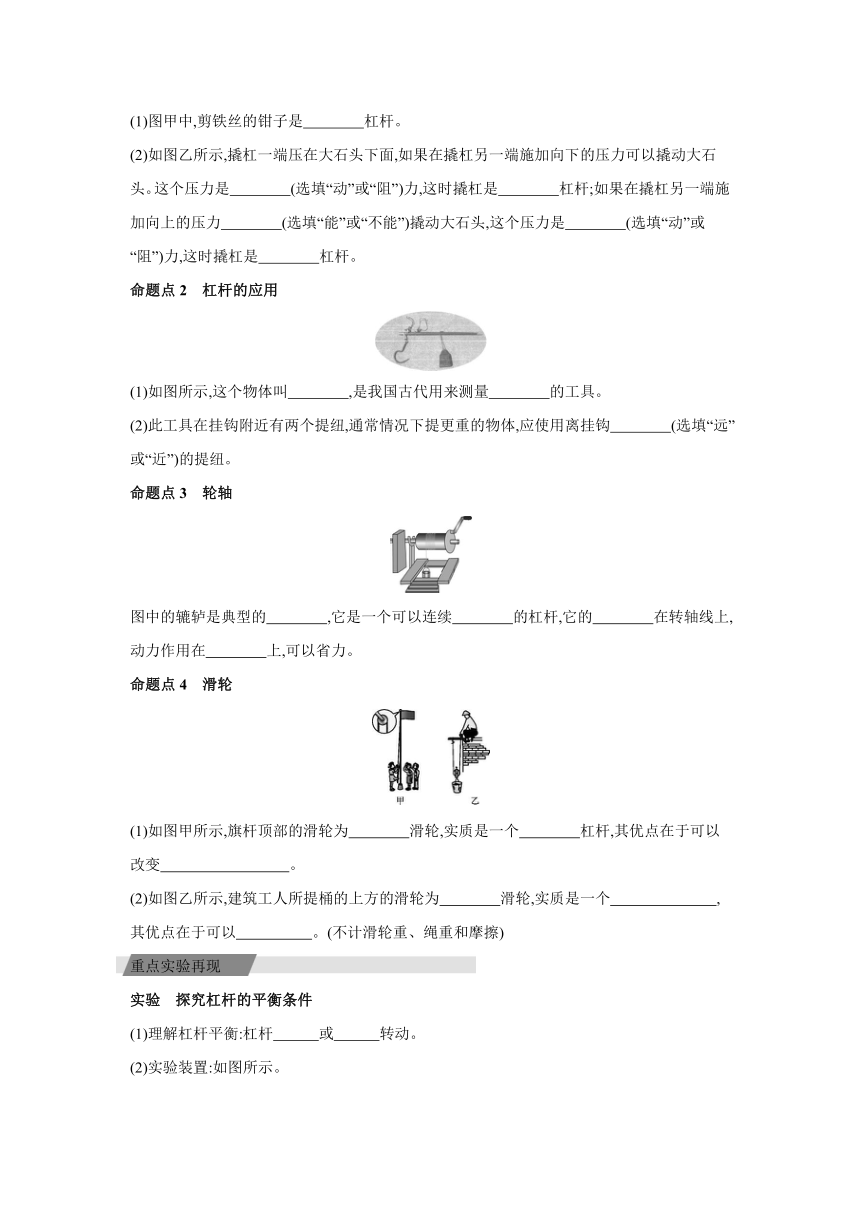
(1)图甲中,剪铁丝的钳子是 杠杆。
(2)如图乙所示,撬杠一端压在大石头下面,如果在撬杠另一端施加向下的压力可以撬动大石头。这个压力是 (选填“动”或“阻”)力,这时撬杠是 杠杆;如果在撬杠另一端施加向上的压力 (选填“能”或“不能”)撬动大石头,这个压力是 (选填“动”或“阻”)力,这时撬杠是 杠杆。
命题点2 杠杆的应用
(1)如图所示,这个物体叫 ,是我国古代用来测量 的工具。
(2)此工具在挂钩附近有两个提纽,通常情况下提更重的物体,应使用离挂钩 (选填“远”或“近”)的提纽。
命题点3 轮轴
图中的辘轳是典型的 ,它是一个可以连续 的杠杆,它的 在转轴线上,动力作用在 上,可以省力。
命题点4 滑轮
(1)如图甲所示,旗杆顶部的滑轮为 滑轮,实质是一个 杠杆,其优点在于可以改变 。
(2)如图乙所示,建筑工人所提桶的上方的滑轮为 滑轮,实质是一个 ,其优点在于可以 。(不计滑轮重、绳重和摩擦)
重点实验再现
实验 探究杠杆的平衡条件
(1)理解杠杆平衡:杠杆 或 转动。
(2)实验装置:如图所示。
(3)进行实验:①调节杠杆两端的 ,使杠杆在 位置平衡,目的是消除杠杆 对杠杆平衡的影响。
②实验过程中移动钩码位置使杠杆再次在 位置平衡,目的是便于从杠杆上直接读出 。
③改变力和力臂数值,再做几次实验。
(4)得出结论: (文字表达式)。写成公式为 或 。
(5)评估交流:①实验结束后,有的同学发现,杠杆的平衡条件也可以表达为“动力+动力臂=
阻力+阻力臂”,你同意这个观点吗 请说明理由: 。
②为了方便确定力的大小,如图所示,有的同学想到用弹簧测力计来代替钩码直接读取示数。开始用弹簧测力计在C处竖直向上拉,使杠杆保持水平平衡。他们发现若使弹簧测力计逐渐向右倾斜仍然保持杠杆水平平衡,拉力F就变大了,你认为原因是 。
中考真题链接
类型一 杠杆类型的识别
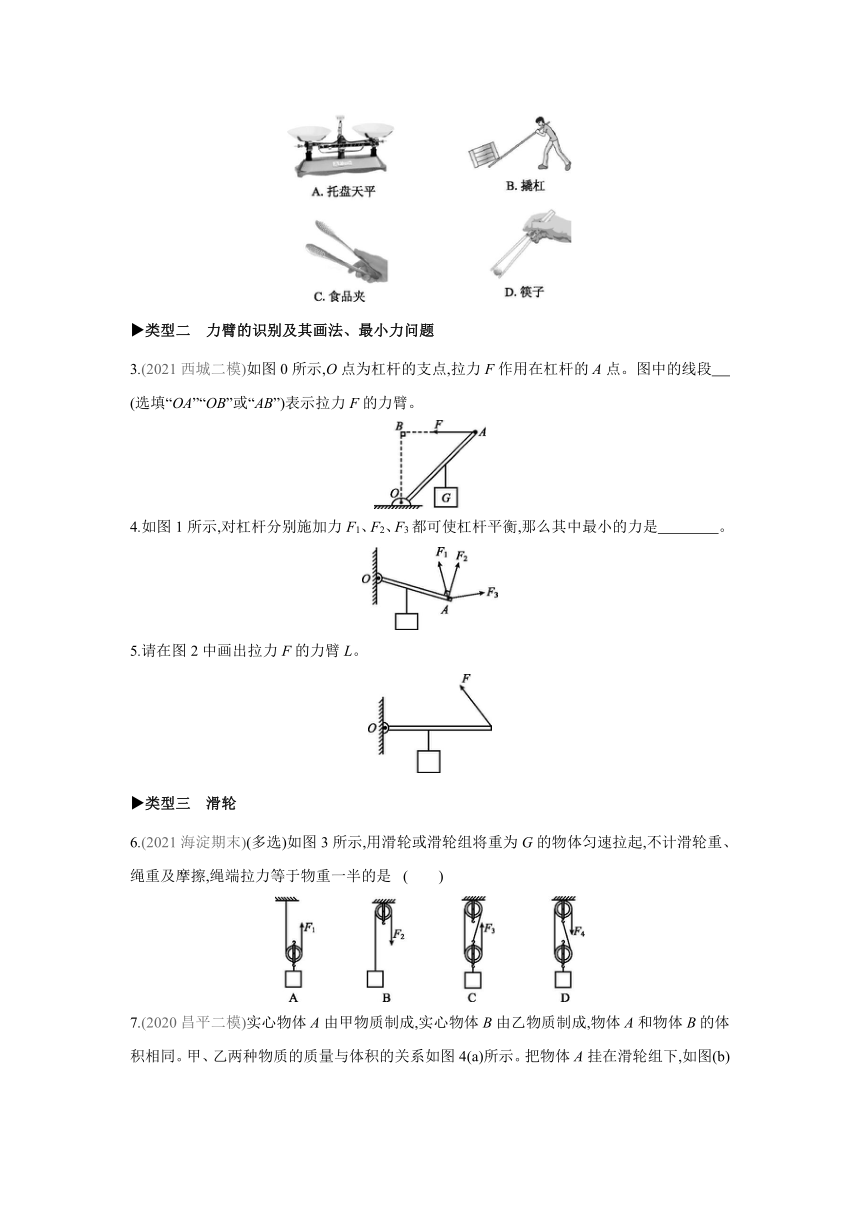
1.(2020北京)如图所示的四种工具中,正常使用时属于费力杠杆的是 ( )
2.(2021顺义一模)如图所示的工具在正常使用时,属于省力杠杆的是 ( )
类型二 力臂的识别及其画法、最小力问题
3.(2021西城二模)如图0所示,O点为杠杆的支点,拉力F作用在杠杆的A点。图中的线段 (选填“OA”“OB”或“AB”)表示拉力F的力臂。
4.如图1所示,对杠杆分别施加力F1、F2、F3都可使杠杆平衡,那么其中最小的力是 。
5.请在图2中画出拉力F的力臂L。
类型三 滑轮
6.(2021海淀期末)(多选)如图3所示,用滑轮或滑轮组将重为G的物体匀速拉起,不计滑轮重、绳重及摩擦,绳端拉力等于物重一半的是 ( )
7.(2020昌平二模)实心物体A由甲物质制成,实心物体B由乙物质制成,物体A和物体B的体积相同。甲、乙两种物质的质量与体积的关系如图4(a)所示。把物体A挂在滑轮组下,如图(b)所示,若使滑轮组处于静止状态,则虚线框内应悬挂物体B的个数是(不计绳重、滑轮重及摩擦) ( )
A.1 B.2 C.3 D.4
8.(2020朝阳二模)组装如图5所示的滑轮组,画出滑轮组的绕线,使绳子自由端最省力。
类型四 杠杆平衡条件的应用
9.(2021海淀模拟)如图6所示,重力为G的均匀木棒竖直悬于O点,在其下端施加始终垂直于棒的拉力F,让木棒缓慢转到图中虚线所示位置,在转动的过程中 ( )
A.拉力F逐渐变大 B.拉力F逐渐变小
C.拉力F一直不变 D.无法确定拉力F的大小
10.(2021东城模拟)当你将小臂平举,并用手掌托住一只铁球时,肱二头肌会垂直于小臂向上施加一个拉力,此时整个小臂就是一个杠杆,球压在掌心上的力是阻力(忽略小臂自重),肘关节位置相当于支点(如图7所示),已知肱二头肌拉伸点到铁球重力作用线的距离为25 cm,铁球的质量为4.2 kg,小臂总长(肘关节到掌心)为30 cm,则小臂平抬铁球时,肱二头肌的拉伸力至少为(g取10 N/kg) ( )
A.5.04 N B.50.4 N C.210 N D.252 N
11.(2020密云一模)如图8所示,将重为150 N的甲物体用细绳挂在轻质杠杆的A端,杠杆的B端悬挂乙物体,杠杆在水平位置平衡。已知乙物体所受重力为30 N,AO∶OB=1∶3,甲物体的底面积为0.2 m2,g取10 N/kg。下列说法中正确的是 ( )
A.甲物体对杠杆的拉力为10 N
B.杠杆对甲物体竖直向上的拉力为60 N
C.甲物体对水平地面的压强为750 Pa
D.水平地面对甲物体的支持力为60 N
12.(2021丰台二模)如图9甲所示是中国农村历代通用的旧式提水器具——桔槔,这种提水工具虽简单,但它使劳动人民的劳动强度得以减轻。桔槔的结构相当于一个普通的杠杆,如图乙所示。轻质细杆AB代表桔槔,O为支点。当水桶中装满水,人使用桔槔缓慢匀速提升水桶时,杠杆A端水桶和水的总重力为G1,人向上提升水桶的拉力为F,杠杆B端重石的重力为G2。下列说法正确的是 ( )
A.人使用桔槔提水比直接用水桶提水费力
B.人使用桔槔匀速向上提水时,杠杆A端受到的拉力大小为G1+F
C.人使用桔槔匀速向上提水时,杠杆满足条件:(G1-F)·OA=G2·AB
D.当重石的重力G2增大时,人使用桔槔提升水桶时的拉力F变小
13.(2020西城二模)小军利用如图0所示的装置测量某液体的密度ρ,他将同种材料制成的甲、乙两物块分别悬挂在轻质硬杆AB的两端,把甲浸没在待测液体中,调节乙的位置到C处时,硬杆AB恰好水平平衡。已知OC=2OA,甲、乙的体积之比为13∶2,甲、乙两物块的密度为2.6 g/cm3。下列说法中正确的是 ( )
图0
A.ρ=0.8×103 kg/m3 B.ρ=1.0×103 kg/m3
C.ρ=1.8×103 kg/m3 D.ρ=2.6×103 kg/m3
14.(2021东城一模)桔槔是利用杠杆原理工作的取水工具,如图1甲所示是我国古代劳动人民利用桔槔灌溉的场景。为了更好地研究该场景中的桔槔配重对需要搬动的重物的影响,小东将桔槔抽象成简单的杠杆模型,如图乙所示,轻质细杆AB代表桔槔,质量较大的物块M模拟重物,质量较小的物块m模拟搬动重物时的配重。支点O在AB的中点,M放置在水平地面上并用细绳悬挂在A点,m悬挂在杠杆上C点,C点可以在OB之间根据需要移动位置,l表示OC的长度。用Ta表示细绳对A点的拉力,T表示细绳对C点的拉力,F表示地面对M的支持力,p表示M对地面的压强。已知AB始终保持水平平衡,则如图2所示关于Ta、T、F、p随l变化关系的图像中正确的是 ( )
类型五 与杠杆有关的探究实验
15.(2021丰台一模)小丰用如图3所示的实验装置探究杠杆的平衡条件,使用的每个钩码质量均相等,杠杆上相邻刻线间的距离相等。
(1)挂钩码前,杠杆在如图甲所示的位置静止,此时杠杆 (选填“处于”或“不处于”)平衡状态;实验时,我们通常会调节平衡螺母使杠杆处于水平平衡,其目的是 。
(2)杠杆水平平衡后,小丰在图乙的A处挂2个钩码,为了使杠杆再次处于水平平衡,应在B处挂 个钩码。
(3)小丰多次实验后,根据所得数据绘制成如图丙所示的L2和F2的关系图像。他发现这和数学课上学过的反比例函数y=的图像很相似。为了进一步确定L2和F2的函数关系,他应该利用以上数据作L2和 之间的关系图像。
16.(2021房山一模)小华用如图4所示的装置探究杠杆的平衡条件,每个钩码的质量均相等,杠杆上相邻刻线间的距离相等。如图甲所示,为使杠杆在水平位置平衡,应将右端的平衡螺母向 调节。杠杆水平平衡后,在杠杆上的A点挂2个钩码,如图乙所示,为使杠杆保持水平平衡,应在B点悬挂 个钩码。如图丙所示,保持杠杆水平平衡,将弹簧测力计在C位置由竖直向上拉改为向左上方斜拉,弹簧测力计的示数会变大,请分析弹簧测力计示数变大的原因: 。
类型六 与杠杆有关的计算
17.(2020丰台二模)图5是挖井时从井中提升沙土的杠杆示意图。杠杆AB可以在竖直平面内绕固定点O转动,已知AO∶OB=3∶2,悬挂在A端的桶与沙土所受的总重力为300 N,当人站在水平地面上,对杠杆B端施加竖直向下的拉力F时,杠杆AB在水平位置平衡,已知人所受的重力为600 N,人的双脚与地面的接触面积为0.05 m2,不计杆重和绳重。求:
(1)拉力F的大小。
(2)人对水平地面的压强。
答案
一、1.转动
2.(1)绕着转动 (2)驱使 (3)阻碍
(4)支点 动力作用线 (5)支点 阻力作用线
3.(1)动力×动力臂=阻力×阻力臂
(2)F1L1=F2L2
4.> 费 < 费 =
二、1.旋转 2.省力 费力 3.汽车方向盘 绞盘
三、1.改变用力的方向 省力 = = 等臂
2.省力 改变用力的方向 2
动力臂是阻力臂二倍的杠杆
3.省力 改变用力的方向
几分之一 F= s=nh
【教材图片解读】
命题点1 (1)省力 (2)动 省力 能 动 省力
命题点2 (1)杆秤 质量 (2)近
命题点3 轮轴 旋转 支点 轮
命题点4 (1)定 等臂 用力的方向
(2)动 动力臂是阻力臂二倍的杠杆 省一半力
【重点实验再现】
实验 (1)静止 匀速
(3)①平衡螺母 水平 自重
②水平 力臂
(4)动力×动力臂=阻力×阻力臂
F1L1= F2L2 =
(5)①不同意;他们的实验数据具有偶然性,并且两个单位不同的物理量是不能相加的
②弹簧测力计在向右倾斜的过程中,动力臂变小了,若杠杆仍要保持水平平衡,则在阻力和阻力臂不变的情况下,动力要变大
【中考真题链接】
1.D 羊角锤、核桃夹、园艺剪在正常使用过程中,动力臂大于阻力臂,是省力杠杆;食品夹在正常使用过程中,动力臂小于阻力臂,是费力杠杆。
2.B
3.OB 从支点O向力F的作用线的延长线作垂线,此垂线段OB即为力F的力臂。
4.F2 由图可知,O为支点,分别画F1、F2、F3的力臂,F1、F3对应的力臂都小于F2对应的力臂L2,所以L2是最长的动力臂;由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂一定的情况下,动力臂越长则动力越小;因为F2对应的动力臂最长,所以F2最小。
5.如图所示
6.AD 不计滑轮重、绳重及摩擦,图A中使用的是动滑轮,能省一半的力,拉力F1=G,故A正确;图B中使用的是定滑轮,不能省力,拉力F2=G,故B错误;图C中使用的是滑轮组,n=3,拉力F3=G,故C错误;图D中使用的是滑轮组,n'=2,拉力F4=G,故D正确。
7.B 由图(a)可知,两种物质的密度分别为ρA===2 g/cm3,ρB===
0.5 g/cm3,则体积相等时,它们的质量和重力的关系分别为mA=4mB,GA=4GB;图(b)中的滑轮组,n=2,那么F==2GB,则要使滑轮组保持静止状态,需挂2个物体B。
8.如图所示
9.A 将木棒缓慢地由最初位置拉到图中虚线所示位置,拉力F始终垂直于木棒,则动力臂不变;阻力为杠杆的重力,其大小不变,当木棒在竖直位置时,重力的力臂为0,转过一定角度后,重力的力臂(阻力臂)逐渐变大;因阻力(即重力)不变,阻力臂变大,动力臂不变,所以,由杠杆的平衡条件F1L1=F2L2可知,动力F变大,故A正确。
10.D 由题意可知,阻力大小为F2=G=mg=4.2 kg×10 N/kg=42 N;
阻力臂:L2=30 cm=0.3 m;
动力臂最大为L1=30 cm-25 cm=5 cm=0.05 m;
根据杠杆平衡条件F1L1=F2L2可得,F1×0.05 m=42 N×0.3 m,
故动力即肱二头肌的拉伸力至少为F1=252 N。
11.D 由杠杆平衡条件F1L1=F2L2可得,F·OA=G乙·OB,从而推导出F==90 N,即甲物体对杠杆的拉力F为90 N,杠杆对甲物体竖直向上的拉力F'与F是一对相互作用力,大小相等,即F'=F=90 N,故选项A、B不符合题意;甲物体受到的支持力:F支=G甲-F'=150 N-
90 N=60 N,故选项D符合题意;甲物体对水平地面的压力F压=F支=60 N,p===300 Pa,故选项C不符合题意。
12.D
13.C 甲浸没在待测液体中,调节乙的位置到C处时,硬杆AB恰好水平平衡,根据杠杆平衡条件可得(G甲-F浮)·OA=G乙·OC,即(ρ甲gV甲-ρgV甲)·OA=ρ乙gV乙·OC;化简可得
(ρ甲-ρ)V甲·OA=ρ乙V乙·OC,将已知条件代入上式可得,(2.6 g/cm3-ρ)6.5V乙·OA=
2.6 g/cm3×V乙·2OA,解得ρ=1.8×103 kg/m3。
14.D 轻质细杆AB相当于一个杠杆,根据杠杆的平衡条件可知,Tl=TalOA。
m向左移动的过程中,l变大,由于物体m的质量不变,重力不变,对C点的拉力不变,即T保持不变,故B错误;lOA不变,l变大,根据杠杆的平衡条件可知,Ta=,Ta与l成正比,故A错误;对M受力分析,M受到竖直向下的重力、竖直向上的拉力和支持力,拉力等于Ta,M受到的重力不变,Ta变大,则地面对M的支持力变小,故C错误;根据p=可知,受力面积不变,l变大,地面对M的支持力变小,M对地面的压力减小,则压强变小,故D正确。
15.(1)处于 消除杠杆自重对杠杆平衡的影响;便于在杠杆上直接读出力臂
(2)3 (3)
(1)由题可知,杠杆静止,故图甲中杠杆处于平衡状态;实验时,调节平衡螺母使杠杆处于水平平衡的目的是消除杠杆自重对杠杆平衡的影响,便于在杠杆上直接读出力臂。
(2)杠杆水平平衡后,在图乙的A处挂2个钩码,设每个钩码的重力为G,杠杆每格长度为l,根据杠杆平衡条件F1L1=F2L2,则2G×3l=nG×2l,解得n=3,即为了使杠杆再次处于水平平衡,应在B处挂3个钩码。
(3)为了进一步确定L2和F2的函数关系,应该利用以上数据做L2和之间的关系图像,如果与L2和之间的关系图像是正比例函数图像,则L2和F2成反比,图丙就是反比例函数图像。
16.右 4 阻力和阻力臂的乘积不变,动力臂变小,动力变大
(1)由图甲可知,杠杆的右端高,为使杠杆在水平位置平衡,应将平衡螺母向右端移动。
(2)设一个钩码的重力为G,一格的长度为L,根据杠杆的平衡条件可得2G×4L=nG×2L,解得n=4,故为使杠杆保持水平平衡,应在B点悬挂4个钩码。
(3)杠杆的平衡条件是动力×动力臂=阻力×阻力臂,将弹簧测力计在C位置由竖直向上拉改为向左上方斜拉,阻力和阻力臂的乘积不变,动力臂变小,故动力会变大,弹簧测力计的示数会变大。
17.(1)杠杆水平平衡,由杠杆平衡条件可得,F×OB=GA×AO,所以拉力F的大小:
F===450 N。
(2)人在B端施加竖直向下、大小为450 N的拉力时,人受到绳子的拉力为F拉=450 N,人受到地面的支持力:
F支=G人-F拉=600 N-450 N=150 N,
因此,人对地面的压力为F压=150 N,
人对水平地面的压强:p===3000 Pa。
核心要点突破
一、杠杆
1.定义:我们把绕固定点 的棒、杆或硬件等叫作杠杆。
2.五要素
(1)支点:杠杆 的固定点,如图中O点。
(2)动力: 杠杆转动的力,如图中F1。
(3)阻力: 杠杆转动的力,如图中F2。
(4)动力臂:从 到 的距离,如图中L1。
(5)阻力臂:从 到 的距离,如图中L2。
3.平衡条件
(1)文字表达式: 。
(2)字母表达式: 。
4.三种杠杆的分类
名称 特征 特点 应用举例
省力 杠杆 动力臂 阻力臂 省力、 距离 撬杠、铡刀、动滑轮、羊角锤、钢丝钳、手推车、花枝剪刀等
费力 杠杆 动力臂 阻力臂 力、省距离 缝纫机踏板、钓鱼竿、人的前臂、理发剪刀等
等臂 杠杆 动力臂 阻力臂 不省力、不费力 托盘天平、定滑轮等
二、轮轴
1.定义:由轮和轴组成,能绕共同轴线 的简单机械叫作轮轴。
2.工作特点:动力作用在轮上是 杠杆;动力作用在轴上是 杠杆。(均选填“省力”或“费力”)
3.生活中常见的轮轴类机械有 和 等。
三、滑轮
1.定滑轮的特点:可以 ,但不能 ;即F G, s h。定滑轮实质是一个 杠杆。
2.动滑轮的特点:可以 ,但不能 ;即F= G, s= h(在忽略滑轮重、绳重和摩擦的情况下)。动滑轮实质是一个 。
3.滑轮组的特点:既可以 ,又可以 。
关系:在忽略绳重、滑轮重和摩擦的情况下,动滑轮上有几段绳子承担物重,所用拉力就是物重的 ,即 ;绳端移动的距离就是物体上升高度的几倍,即 。
教材知识纵横
定滑轮、动滑轮、滑轮组的区别与联系
名称 定义 实质 特点 图示
轴固定不动的滑轮 等臂 杠杆 不省力,但可以改变用力的方向
轴跟物体一起运动的滑轮 动力臂为阻力臂二倍的杠 杆 能省一半的力,但不能改变用力的方向
由定滑轮和动滑轮组合而成 ①在忽略摩擦和绳重的情况下,使用滑轮组时,重物和动滑轮总重由几段绳子承担,提起重物所用的力就等于总重的几分之一,即F=; ②既可以省力,又可以改变用力的方向
命题点1 杠杆的分类
(1)图甲中,剪铁丝的钳子是 杠杆。
(2)如图乙所示,撬杠一端压在大石头下面,如果在撬杠另一端施加向下的压力可以撬动大石头。这个压力是 (选填“动”或“阻”)力,这时撬杠是 杠杆;如果在撬杠另一端施加向上的压力 (选填“能”或“不能”)撬动大石头,这个压力是 (选填“动”或“阻”)力,这时撬杠是 杠杆。
命题点2 杠杆的应用
(1)如图所示,这个物体叫 ,是我国古代用来测量 的工具。
(2)此工具在挂钩附近有两个提纽,通常情况下提更重的物体,应使用离挂钩 (选填“远”或“近”)的提纽。
命题点3 轮轴
图中的辘轳是典型的 ,它是一个可以连续 的杠杆,它的 在转轴线上,动力作用在 上,可以省力。
命题点4 滑轮
(1)如图甲所示,旗杆顶部的滑轮为 滑轮,实质是一个 杠杆,其优点在于可以改变 。
(2)如图乙所示,建筑工人所提桶的上方的滑轮为 滑轮,实质是一个 ,其优点在于可以 。(不计滑轮重、绳重和摩擦)
重点实验再现
实验 探究杠杆的平衡条件
(1)理解杠杆平衡:杠杆 或 转动。
(2)实验装置:如图所示。
(3)进行实验:①调节杠杆两端的 ,使杠杆在 位置平衡,目的是消除杠杆 对杠杆平衡的影响。
②实验过程中移动钩码位置使杠杆再次在 位置平衡,目的是便于从杠杆上直接读出 。
③改变力和力臂数值,再做几次实验。
(4)得出结论: (文字表达式)。写成公式为 或 。
(5)评估交流:①实验结束后,有的同学发现,杠杆的平衡条件也可以表达为“动力+动力臂=
阻力+阻力臂”,你同意这个观点吗 请说明理由: 。
②为了方便确定力的大小,如图所示,有的同学想到用弹簧测力计来代替钩码直接读取示数。开始用弹簧测力计在C处竖直向上拉,使杠杆保持水平平衡。他们发现若使弹簧测力计逐渐向右倾斜仍然保持杠杆水平平衡,拉力F就变大了,你认为原因是 。
中考真题链接
类型一 杠杆类型的识别
1.(2020北京)如图所示的四种工具中,正常使用时属于费力杠杆的是 ( )
2.(2021顺义一模)如图所示的工具在正常使用时,属于省力杠杆的是 ( )
类型二 力臂的识别及其画法、最小力问题
3.(2021西城二模)如图0所示,O点为杠杆的支点,拉力F作用在杠杆的A点。图中的线段 (选填“OA”“OB”或“AB”)表示拉力F的力臂。
4.如图1所示,对杠杆分别施加力F1、F2、F3都可使杠杆平衡,那么其中最小的力是 。
5.请在图2中画出拉力F的力臂L。
类型三 滑轮
6.(2021海淀期末)(多选)如图3所示,用滑轮或滑轮组将重为G的物体匀速拉起,不计滑轮重、绳重及摩擦,绳端拉力等于物重一半的是 ( )
7.(2020昌平二模)实心物体A由甲物质制成,实心物体B由乙物质制成,物体A和物体B的体积相同。甲、乙两种物质的质量与体积的关系如图4(a)所示。把物体A挂在滑轮组下,如图(b)所示,若使滑轮组处于静止状态,则虚线框内应悬挂物体B的个数是(不计绳重、滑轮重及摩擦) ( )
A.1 B.2 C.3 D.4
8.(2020朝阳二模)组装如图5所示的滑轮组,画出滑轮组的绕线,使绳子自由端最省力。
类型四 杠杆平衡条件的应用
9.(2021海淀模拟)如图6所示,重力为G的均匀木棒竖直悬于O点,在其下端施加始终垂直于棒的拉力F,让木棒缓慢转到图中虚线所示位置,在转动的过程中 ( )
A.拉力F逐渐变大 B.拉力F逐渐变小
C.拉力F一直不变 D.无法确定拉力F的大小
10.(2021东城模拟)当你将小臂平举,并用手掌托住一只铁球时,肱二头肌会垂直于小臂向上施加一个拉力,此时整个小臂就是一个杠杆,球压在掌心上的力是阻力(忽略小臂自重),肘关节位置相当于支点(如图7所示),已知肱二头肌拉伸点到铁球重力作用线的距离为25 cm,铁球的质量为4.2 kg,小臂总长(肘关节到掌心)为30 cm,则小臂平抬铁球时,肱二头肌的拉伸力至少为(g取10 N/kg) ( )
A.5.04 N B.50.4 N C.210 N D.252 N
11.(2020密云一模)如图8所示,将重为150 N的甲物体用细绳挂在轻质杠杆的A端,杠杆的B端悬挂乙物体,杠杆在水平位置平衡。已知乙物体所受重力为30 N,AO∶OB=1∶3,甲物体的底面积为0.2 m2,g取10 N/kg。下列说法中正确的是 ( )
A.甲物体对杠杆的拉力为10 N
B.杠杆对甲物体竖直向上的拉力为60 N
C.甲物体对水平地面的压强为750 Pa
D.水平地面对甲物体的支持力为60 N
12.(2021丰台二模)如图9甲所示是中国农村历代通用的旧式提水器具——桔槔,这种提水工具虽简单,但它使劳动人民的劳动强度得以减轻。桔槔的结构相当于一个普通的杠杆,如图乙所示。轻质细杆AB代表桔槔,O为支点。当水桶中装满水,人使用桔槔缓慢匀速提升水桶时,杠杆A端水桶和水的总重力为G1,人向上提升水桶的拉力为F,杠杆B端重石的重力为G2。下列说法正确的是 ( )
A.人使用桔槔提水比直接用水桶提水费力
B.人使用桔槔匀速向上提水时,杠杆A端受到的拉力大小为G1+F
C.人使用桔槔匀速向上提水时,杠杆满足条件:(G1-F)·OA=G2·AB
D.当重石的重力G2增大时,人使用桔槔提升水桶时的拉力F变小
13.(2020西城二模)小军利用如图0所示的装置测量某液体的密度ρ,他将同种材料制成的甲、乙两物块分别悬挂在轻质硬杆AB的两端,把甲浸没在待测液体中,调节乙的位置到C处时,硬杆AB恰好水平平衡。已知OC=2OA,甲、乙的体积之比为13∶2,甲、乙两物块的密度为2.6 g/cm3。下列说法中正确的是 ( )
图0
A.ρ=0.8×103 kg/m3 B.ρ=1.0×103 kg/m3
C.ρ=1.8×103 kg/m3 D.ρ=2.6×103 kg/m3
14.(2021东城一模)桔槔是利用杠杆原理工作的取水工具,如图1甲所示是我国古代劳动人民利用桔槔灌溉的场景。为了更好地研究该场景中的桔槔配重对需要搬动的重物的影响,小东将桔槔抽象成简单的杠杆模型,如图乙所示,轻质细杆AB代表桔槔,质量较大的物块M模拟重物,质量较小的物块m模拟搬动重物时的配重。支点O在AB的中点,M放置在水平地面上并用细绳悬挂在A点,m悬挂在杠杆上C点,C点可以在OB之间根据需要移动位置,l表示OC的长度。用Ta表示细绳对A点的拉力,T表示细绳对C点的拉力,F表示地面对M的支持力,p表示M对地面的压强。已知AB始终保持水平平衡,则如图2所示关于Ta、T、F、p随l变化关系的图像中正确的是 ( )
类型五 与杠杆有关的探究实验
15.(2021丰台一模)小丰用如图3所示的实验装置探究杠杆的平衡条件,使用的每个钩码质量均相等,杠杆上相邻刻线间的距离相等。
(1)挂钩码前,杠杆在如图甲所示的位置静止,此时杠杆 (选填“处于”或“不处于”)平衡状态;实验时,我们通常会调节平衡螺母使杠杆处于水平平衡,其目的是 。
(2)杠杆水平平衡后,小丰在图乙的A处挂2个钩码,为了使杠杆再次处于水平平衡,应在B处挂 个钩码。
(3)小丰多次实验后,根据所得数据绘制成如图丙所示的L2和F2的关系图像。他发现这和数学课上学过的反比例函数y=的图像很相似。为了进一步确定L2和F2的函数关系,他应该利用以上数据作L2和 之间的关系图像。
16.(2021房山一模)小华用如图4所示的装置探究杠杆的平衡条件,每个钩码的质量均相等,杠杆上相邻刻线间的距离相等。如图甲所示,为使杠杆在水平位置平衡,应将右端的平衡螺母向 调节。杠杆水平平衡后,在杠杆上的A点挂2个钩码,如图乙所示,为使杠杆保持水平平衡,应在B点悬挂 个钩码。如图丙所示,保持杠杆水平平衡,将弹簧测力计在C位置由竖直向上拉改为向左上方斜拉,弹簧测力计的示数会变大,请分析弹簧测力计示数变大的原因: 。
类型六 与杠杆有关的计算
17.(2020丰台二模)图5是挖井时从井中提升沙土的杠杆示意图。杠杆AB可以在竖直平面内绕固定点O转动,已知AO∶OB=3∶2,悬挂在A端的桶与沙土所受的总重力为300 N,当人站在水平地面上,对杠杆B端施加竖直向下的拉力F时,杠杆AB在水平位置平衡,已知人所受的重力为600 N,人的双脚与地面的接触面积为0.05 m2,不计杆重和绳重。求:
(1)拉力F的大小。
(2)人对水平地面的压强。
答案
一、1.转动
2.(1)绕着转动 (2)驱使 (3)阻碍
(4)支点 动力作用线 (5)支点 阻力作用线
3.(1)动力×动力臂=阻力×阻力臂
(2)F1L1=F2L2
4.> 费 < 费 =
二、1.旋转 2.省力 费力 3.汽车方向盘 绞盘
三、1.改变用力的方向 省力 = = 等臂
2.省力 改变用力的方向 2
动力臂是阻力臂二倍的杠杆
3.省力 改变用力的方向
几分之一 F= s=nh
【教材图片解读】
命题点1 (1)省力 (2)动 省力 能 动 省力
命题点2 (1)杆秤 质量 (2)近
命题点3 轮轴 旋转 支点 轮
命题点4 (1)定 等臂 用力的方向
(2)动 动力臂是阻力臂二倍的杠杆 省一半力
【重点实验再现】
实验 (1)静止 匀速
(3)①平衡螺母 水平 自重
②水平 力臂
(4)动力×动力臂=阻力×阻力臂
F1L1= F2L2 =
(5)①不同意;他们的实验数据具有偶然性,并且两个单位不同的物理量是不能相加的
②弹簧测力计在向右倾斜的过程中,动力臂变小了,若杠杆仍要保持水平平衡,则在阻力和阻力臂不变的情况下,动力要变大
【中考真题链接】
1.D 羊角锤、核桃夹、园艺剪在正常使用过程中,动力臂大于阻力臂,是省力杠杆;食品夹在正常使用过程中,动力臂小于阻力臂,是费力杠杆。
2.B
3.OB 从支点O向力F的作用线的延长线作垂线,此垂线段OB即为力F的力臂。
4.F2 由图可知,O为支点,分别画F1、F2、F3的力臂,F1、F3对应的力臂都小于F2对应的力臂L2,所以L2是最长的动力臂;由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂一定的情况下,动力臂越长则动力越小;因为F2对应的动力臂最长,所以F2最小。
5.如图所示
6.AD 不计滑轮重、绳重及摩擦,图A中使用的是动滑轮,能省一半的力,拉力F1=G,故A正确;图B中使用的是定滑轮,不能省力,拉力F2=G,故B错误;图C中使用的是滑轮组,n=3,拉力F3=G,故C错误;图D中使用的是滑轮组,n'=2,拉力F4=G,故D正确。
7.B 由图(a)可知,两种物质的密度分别为ρA===2 g/cm3,ρB===
0.5 g/cm3,则体积相等时,它们的质量和重力的关系分别为mA=4mB,GA=4GB;图(b)中的滑轮组,n=2,那么F==2GB,则要使滑轮组保持静止状态,需挂2个物体B。
8.如图所示
9.A 将木棒缓慢地由最初位置拉到图中虚线所示位置,拉力F始终垂直于木棒,则动力臂不变;阻力为杠杆的重力,其大小不变,当木棒在竖直位置时,重力的力臂为0,转过一定角度后,重力的力臂(阻力臂)逐渐变大;因阻力(即重力)不变,阻力臂变大,动力臂不变,所以,由杠杆的平衡条件F1L1=F2L2可知,动力F变大,故A正确。
10.D 由题意可知,阻力大小为F2=G=mg=4.2 kg×10 N/kg=42 N;
阻力臂:L2=30 cm=0.3 m;
动力臂最大为L1=30 cm-25 cm=5 cm=0.05 m;
根据杠杆平衡条件F1L1=F2L2可得,F1×0.05 m=42 N×0.3 m,
故动力即肱二头肌的拉伸力至少为F1=252 N。
11.D 由杠杆平衡条件F1L1=F2L2可得,F·OA=G乙·OB,从而推导出F==90 N,即甲物体对杠杆的拉力F为90 N,杠杆对甲物体竖直向上的拉力F'与F是一对相互作用力,大小相等,即F'=F=90 N,故选项A、B不符合题意;甲物体受到的支持力:F支=G甲-F'=150 N-
90 N=60 N,故选项D符合题意;甲物体对水平地面的压力F压=F支=60 N,p===300 Pa,故选项C不符合题意。
12.D
13.C 甲浸没在待测液体中,调节乙的位置到C处时,硬杆AB恰好水平平衡,根据杠杆平衡条件可得(G甲-F浮)·OA=G乙·OC,即(ρ甲gV甲-ρgV甲)·OA=ρ乙gV乙·OC;化简可得
(ρ甲-ρ)V甲·OA=ρ乙V乙·OC,将已知条件代入上式可得,(2.6 g/cm3-ρ)6.5V乙·OA=
2.6 g/cm3×V乙·2OA,解得ρ=1.8×103 kg/m3。
14.D 轻质细杆AB相当于一个杠杆,根据杠杆的平衡条件可知,Tl=TalOA。
m向左移动的过程中,l变大,由于物体m的质量不变,重力不变,对C点的拉力不变,即T保持不变,故B错误;lOA不变,l变大,根据杠杆的平衡条件可知,Ta=,Ta与l成正比,故A错误;对M受力分析,M受到竖直向下的重力、竖直向上的拉力和支持力,拉力等于Ta,M受到的重力不变,Ta变大,则地面对M的支持力变小,故C错误;根据p=可知,受力面积不变,l变大,地面对M的支持力变小,M对地面的压力减小,则压强变小,故D正确。
15.(1)处于 消除杠杆自重对杠杆平衡的影响;便于在杠杆上直接读出力臂
(2)3 (3)
(1)由题可知,杠杆静止,故图甲中杠杆处于平衡状态;实验时,调节平衡螺母使杠杆处于水平平衡的目的是消除杠杆自重对杠杆平衡的影响,便于在杠杆上直接读出力臂。
(2)杠杆水平平衡后,在图乙的A处挂2个钩码,设每个钩码的重力为G,杠杆每格长度为l,根据杠杆平衡条件F1L1=F2L2,则2G×3l=nG×2l,解得n=3,即为了使杠杆再次处于水平平衡,应在B处挂3个钩码。
(3)为了进一步确定L2和F2的函数关系,应该利用以上数据做L2和之间的关系图像,如果与L2和之间的关系图像是正比例函数图像,则L2和F2成反比,图丙就是反比例函数图像。
16.右 4 阻力和阻力臂的乘积不变,动力臂变小,动力变大
(1)由图甲可知,杠杆的右端高,为使杠杆在水平位置平衡,应将平衡螺母向右端移动。
(2)设一个钩码的重力为G,一格的长度为L,根据杠杆的平衡条件可得2G×4L=nG×2L,解得n=4,故为使杠杆保持水平平衡,应在B点悬挂4个钩码。
(3)杠杆的平衡条件是动力×动力臂=阻力×阻力臂,将弹簧测力计在C位置由竖直向上拉改为向左上方斜拉,阻力和阻力臂的乘积不变,动力臂变小,故动力会变大,弹簧测力计的示数会变大。
17.(1)杠杆水平平衡,由杠杆平衡条件可得,F×OB=GA×AO,所以拉力F的大小:
F===450 N。
(2)人在B端施加竖直向下、大小为450 N的拉力时,人受到绳子的拉力为F拉=450 N,人受到地面的支持力:
F支=G人-F拉=600 N-450 N=150 N,
因此,人对地面的压力为F压=150 N,
人对水平地面的压强:p===3000 Pa。
同课章节目录
- 第一章 常见的运动
- 一、长度和时间的测量
- 二、机械运动
- 三、比较运动的快慢
- 四、学生实验:测量速度
- 五、声音的产生和传播
- 六、乐音和噪声
- 七、超声波及其应用
- 课外探究 水杯琴
- 第二章 质量和密度
- 一、质量及测量
- 二、学生实验:测量质量
- 三、物质的密度及其应用
- 四、学生实验:测量密度
- 第三章 运动和力
- 一、力
- 二、力的测量
- 三、重力
- 四、二力平衡
- 五、滑动摩擦力
- 六、运动和力的关系
- 课外探究 防滑运动鞋
- 第四章 压强与浮力
- 一、压力 压强
- 二、探究液体压强
- 三、连通器
- 四、大气压强
- 五、液体的压强与流速的关系
- 六、浮力
- 七、物体的浮沉条件
- 第五章 简单机械
- 一、杠杆
- 二、学生实验:探究杠杆
- 三、滑轮
- 课外探究 变速自行车
- 第六章 功和能
- 一、功
- 二、功率
- 三、功的原理
- 四、机械能
- 第七章 热现象
- 一、温度、温度计
- 二、熔化和凝固
- 三、汽化和液化
- 四、升华和凝华
- 五、物质结构的微观模型
- 六、内能 能量转化
- 七、比热容
- 八、燃料 能源与环保
- 九、热机
- 第八章 光现象
- 一、光的传播
- 二、学生实验:探究光的反射规律
- 三、学生实验:探究平面镜成像
- 四、探究光的折射现象
- 五、透镜
- 六、学生实验:探究凸透镜成像
- 七、生活中的透镜
- 八、眼睛和眼镜
- 九、物体的颜色
