北师大版数学七年级下册 2.4 用尺规作角 课件 (共19张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 2.4 用尺规作角 课件 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 387.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
2.4 用尺规作角
北师大版 数学 七年级 下册
豆豆书上的三角形被墨迹污染了一部分,他想在作业本上画出一个与书上完全一样的三角形,他该怎么办?
你能帮他画出来吗?
导入新知
1. 能按照作图语言来完成作图动作,能用尺规作一个角等于已知角,并了解它在尺规作图中的简单应用.
2. 能利用尺规作角的和、差、倍.
素养目标
3. 在尺规作图过程当中,积累数学活动经验,培养动手能力和逻辑分析能力.
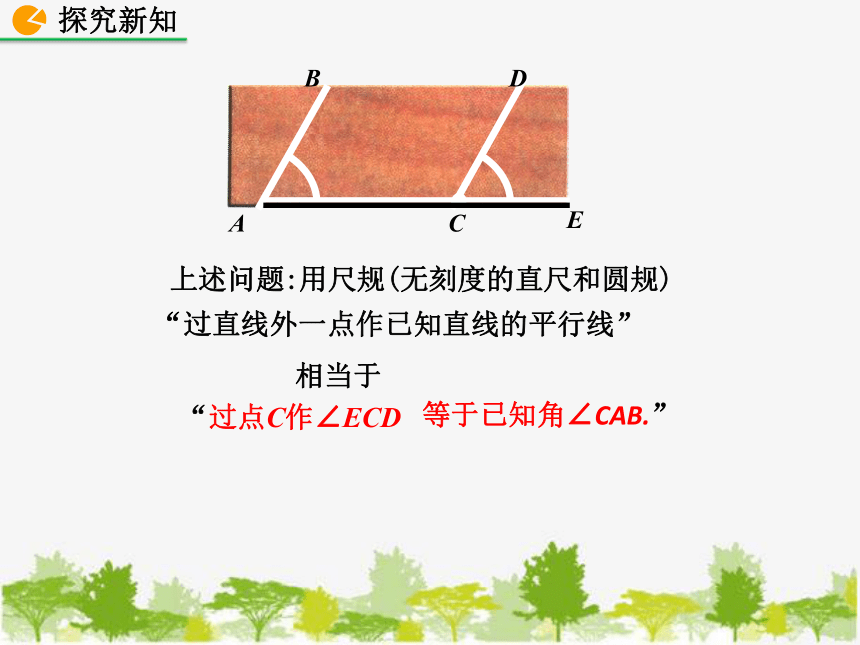
如图,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB.
(1)请过点C画出与AB 平行的另一边.
(2)如果只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?
探究新知
知识点
用尺规作一个角等于已知角
A
B
D
C
上述问题:用尺规(无刻度的直尺和圆规)
“过直线外一点作已知直线的平行线”
相当于
“过点C作∠ECD
E
等于已知角∠CAB.”
探究新知
B
O
A
O’
A’
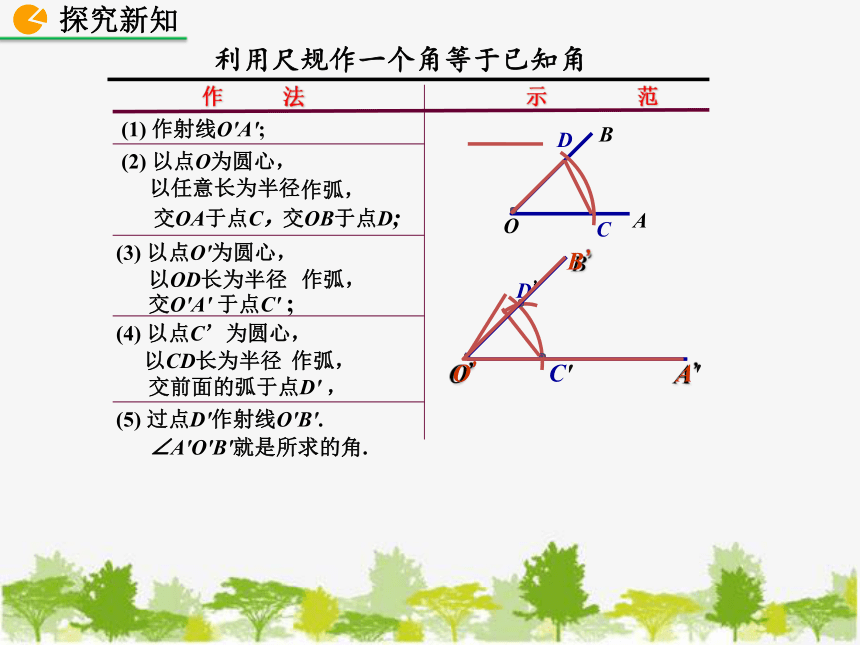
(2) 以点O为圆心,
以任意长为半径
交OA于点C,
(3) 以点O'为圆心,
作弧,
C
D
以OD长为半径
作弧,
C'
(4) 以点C’为圆心,
以CD长为半径
作弧,
D’
(5) 过点D'作射线O'B'.
B’
A'
O’
B’
∠A'O'B'就是所求的角.
作 法 示 范
(1) 作射线O'A';
交OB于点D;
交O'A' 于点C' ;
交前面的弧于点D' ,
探究新知
利用尺规作一个角等于已知角
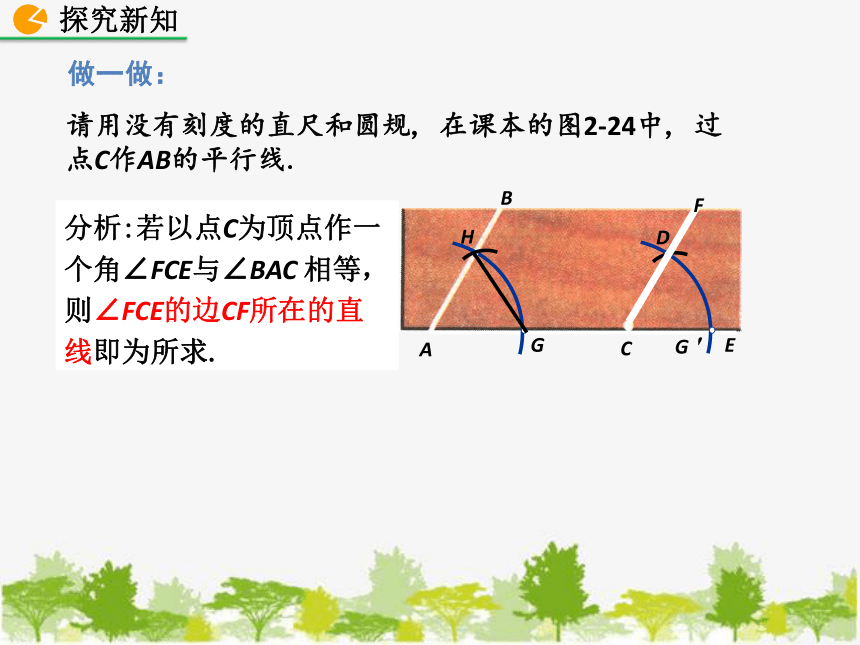
请用没有刻度的直尺和圆规, 在课本的图2-24中, 过点C作AB的平行线.
A
B
C
分析:若以点C为顶点作一个角∠FCE与∠BAC 相等,则∠FCE的边CF所在的直线即为所求..
E
G
G '
H
D
F
探究新知
做一做:
例 如图,已知 线段a 和两条互相垂直的直线AB,CD.
(1) 利用圆规,在射线OA,OB,OC,OD上作线段O' A' ,O'B' ,O' C' ,O' D' ,使它们分别与 线段a 相等.
(2) 依次连接A' ,C' ,B' ,D'你得到了一个怎样的图形?
探究新知
素养考点 1
用尺规作一个角等于已知角
(保留作图痕迹,不写作法)
O
a
A
B
C
D
B '
C '
D '
A '
是一个正方形
探究新知
解:
已知: ∠AOB.
利用尺规作: ∠A' O' B'
使∠A' O' B' =2∠AOB.
B
O
A
独立思考、合作交流;
口述作法、保留作图痕迹.
作法一:
C
A'
B'
∠A'OB'即为所求作的角.
B
O
A
作法二:
C
D
C’
E
B'
O'
A'
∠A'O'B'即为所求作的角.
巩固练习
变式训练
1.(2020 佛山模拟)尺规作图是指( )
A.用直尺规范作图
B.用刻度尺和圆规作图
C.用没有刻度的直尺和圆规作图
D.直尺和圆规是作图工具
C
连接中考
1.下列尺规作图的语句错误的是( )
A.作∠AOB,使∠AOB=3∠α
B.以点O为圆心作弧
C.以点A为圆心,线段a的长为半径作弧
D.作∠ABC,使∠ABC=∠α+∠β
B
课堂检测
基础巩固题
2.下列属于尺规作图的是( )
A.用量角器画一个角等于30°
B.用圆规和直尺作线段AB等于已知线段a
C.用三角板作线段AB的垂线
D.用刻度尺画一条线段等于3 cm
B
课堂检测
基础巩固题
3.画一个钝角∠AOB,然后以O为顶点,以OA为一边, 在角的内部画一条射线OC,使∠AOC=90°,正确的图形是( )
D
课堂检测
基础巩固题
A.
C.
D.
B.
4.已知∠1和∠2,求作一个角,使它等于∠1与∠2的和.
解:如图,∠AOB为所作.
课堂检测
基础巩固题
如图,已知∠A,∠B,求作一个角,使它等于∠A-∠B.(不用写作法,保留作图痕迹)
解:作∠COD=∠A,
并在∠COD的内部作∠DOE=∠B,
则∠COE就是所求作的角.
课堂检测
能力提升题
解:已知:直线l及l外一点P,
求作:直线l′,使l′过P点且l′∥l.
作法:1.过点P任意作直线a与l交于Q.
2.以P为顶点,直线a为角的一边,
在直线a同旁作∠2,使∠2=∠1
(如图),则∠2的另一边所在直线l′即为所求.
过直线外一点P作已知直线l的平行线.
课堂检测
拓广探索题
1.尺规作图的基本步骤:
(1)写出已知.(2)写出求作.(3)写出作法并作图.作图时
要保留_________.有时,根据题目要求,可省略作法.
作图痕迹
2.作一个角等于已知角可以归纳为“一线三弧”
先画一条射线,再作三次弧.其中前两次弧半径相同,而第三次以原角的两边与弧的交点之间的距离为半径.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
2.4 用尺规作角
北师大版 数学 七年级 下册
豆豆书上的三角形被墨迹污染了一部分,他想在作业本上画出一个与书上完全一样的三角形,他该怎么办?
你能帮他画出来吗?
导入新知
1. 能按照作图语言来完成作图动作,能用尺规作一个角等于已知角,并了解它在尺规作图中的简单应用.
2. 能利用尺规作角的和、差、倍.
素养目标
3. 在尺规作图过程当中,积累数学活动经验,培养动手能力和逻辑分析能力.
如图,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB.
(1)请过点C画出与AB 平行的另一边.
(2)如果只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?
探究新知
知识点
用尺规作一个角等于已知角
A
B
D
C
上述问题:用尺规(无刻度的直尺和圆规)
“过直线外一点作已知直线的平行线”
相当于
“过点C作∠ECD
E
等于已知角∠CAB.”
探究新知
B
O
A
O’
A’
(2) 以点O为圆心,
以任意长为半径
交OA于点C,
(3) 以点O'为圆心,
作弧,
C
D
以OD长为半径
作弧,
C'
(4) 以点C’为圆心,
以CD长为半径
作弧,
D’
(5) 过点D'作射线O'B'.
B’
A'
O’
B’
∠A'O'B'就是所求的角.
作 法 示 范
(1) 作射线O'A';
交OB于点D;
交O'A' 于点C' ;
交前面的弧于点D' ,
探究新知
利用尺规作一个角等于已知角
请用没有刻度的直尺和圆规, 在课本的图2-24中, 过点C作AB的平行线.
A
B
C
分析:若以点C为顶点作一个角∠FCE与∠BAC 相等,则∠FCE的边CF所在的直线即为所求..
E
G
G '
H
D
F
探究新知
做一做:
例 如图,已知 线段a 和两条互相垂直的直线AB,CD.
(1) 利用圆规,在射线OA,OB,OC,OD上作线段O' A' ,O'B' ,O' C' ,O' D' ,使它们分别与 线段a 相等.
(2) 依次连接A' ,C' ,B' ,D'你得到了一个怎样的图形?
探究新知
素养考点 1
用尺规作一个角等于已知角
(保留作图痕迹,不写作法)
O
a
A
B
C
D
B '
C '
D '
A '
是一个正方形
探究新知
解:
已知: ∠AOB.
利用尺规作: ∠A' O' B'
使∠A' O' B' =2∠AOB.
B
O
A
独立思考、合作交流;
口述作法、保留作图痕迹.
作法一:
C
A'
B'
∠A'OB'即为所求作的角.
B
O
A
作法二:
C
D
C’
E
B'
O'
A'
∠A'O'B'即为所求作的角.
巩固练习
变式训练
1.(2020 佛山模拟)尺规作图是指( )
A.用直尺规范作图
B.用刻度尺和圆规作图
C.用没有刻度的直尺和圆规作图
D.直尺和圆规是作图工具
C
连接中考
1.下列尺规作图的语句错误的是( )
A.作∠AOB,使∠AOB=3∠α
B.以点O为圆心作弧
C.以点A为圆心,线段a的长为半径作弧
D.作∠ABC,使∠ABC=∠α+∠β
B
课堂检测
基础巩固题
2.下列属于尺规作图的是( )
A.用量角器画一个角等于30°
B.用圆规和直尺作线段AB等于已知线段a
C.用三角板作线段AB的垂线
D.用刻度尺画一条线段等于3 cm
B
课堂检测
基础巩固题
3.画一个钝角∠AOB,然后以O为顶点,以OA为一边, 在角的内部画一条射线OC,使∠AOC=90°,正确的图形是( )
D
课堂检测
基础巩固题
A.
C.
D.
B.
4.已知∠1和∠2,求作一个角,使它等于∠1与∠2的和.
解:如图,∠AOB为所作.
课堂检测
基础巩固题
如图,已知∠A,∠B,求作一个角,使它等于∠A-∠B.(不用写作法,保留作图痕迹)
解:作∠COD=∠A,
并在∠COD的内部作∠DOE=∠B,
则∠COE就是所求作的角.
课堂检测
能力提升题
解:已知:直线l及l外一点P,
求作:直线l′,使l′过P点且l′∥l.
作法:1.过点P任意作直线a与l交于Q.
2.以P为顶点,直线a为角的一边,
在直线a同旁作∠2,使∠2=∠1
(如图),则∠2的另一边所在直线l′即为所求.
过直线外一点P作已知直线l的平行线.
课堂检测
拓广探索题
1.尺规作图的基本步骤:
(1)写出已知.(2)写出求作.(3)写出作法并作图.作图时
要保留_________.有时,根据题目要求,可省略作法.
作图痕迹
2.作一个角等于已知角可以归纳为“一线三弧”
先画一条射线,再作三次弧.其中前两次弧半径相同,而第三次以原角的两边与弧的交点之间的距离为半径.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
