人教版数学八年级下册 第十六章 小结与复习 课件 (共19张PPT)
文档属性
| 名称 | 人教版数学八年级下册 第十六章 小结与复习 课件 (共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 278.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
小结与复习
第十六章 二次根式
1.通过复习理清本章的知识结构和重要知识点.
2.总结本章的重要思想方法和技能技巧.
复习目标:
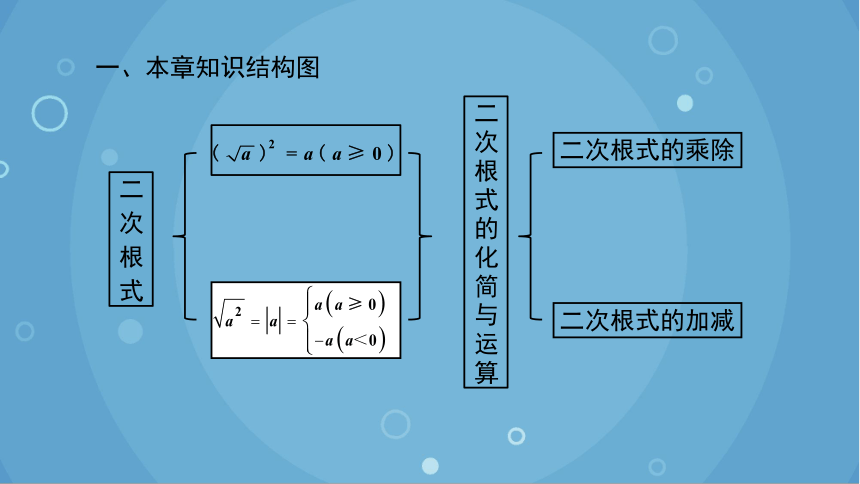
一、本章知识结构图
二次根式
二次根式的化简与运算
二次根式的乘除
二次根式的加减
二、知识梳理
1.二次根式的概念
一般地,形如____(a≥0)的式子叫做二次根式.
对于二次根式的理解:
①带有二次根号;②被开方数是非负数,即a≥0.
[易错点] 二次根式中,被开方数一定是非负数,否则就没有意义.
2.二次根式的性质:
3.最简二次根式
满足下列两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含_______;
(2)被开方数中不含能___________的因数或因式.
开得尽方
分母
5.二次根式的加减:类似合并同类项
可以先将二次根式化成_____________,再将______________
的二次根式进行合并.
被开方数相同
最简二次根式
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
注意平方差公式与完全平方公式的运用!
6.二次根式的混合运算
有理数的混合运算与类似:先算乘(开)方,再算乘除,最后算加减,有括号先算括号里面的.
整式乘法运算中的乘法公式:
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
二次根式的运算律:
(1)实数运算中的运算律(交换律、结合律、分配律)和整式
乘法中的乘法公式在二次根式的运算中仍然适用.
(2)在进行计算时,能用乘法公式的要尽量使用乘法公式,
同时注意合理地运用运算律.
针对练习
1.下列各式: 中,不是二次根式的有 ( )
A.3个 B.4个 C.5个 D.6个
A
2.下列运算正确的是 ( )
C
4.若12
3.若实数a,b满足 则 .
1
5. 若等腰三角形底边长为 ,底边的高为
,则三角形的面积为 .
6.求下列二次根式中字母的取值范围:
解得 - 5≤x<3.
解:(1) 由题意得
∴x=4.
(2) 由题意得
7.将下列各数写成一个非负数的平方的形式:
8. 计算:
解:(1)原式
(2)原式
9. 交警为了估计肇事汽车在出事前的速度,总结出经验公式
,其中v是车速(单位:千米/时),d 是汽车刹车后车轮滑动的距离(单位:米),f 是摩擦系数.在某次交通事故调查中,测得d=20米,f=1.2,请你帮交警计算一下肇事汽车在出事前的速度.
解:根据题意得 (千米/时).
答:肇事汽车在出事前的速度是 千米/时.
解:原式
当 时,
原式
10. 先化简,再求值: ,其中
11. 已知a是实数,求 的值.
解: 分三种情况讨论:
当a≤-2时,原式=(-a-2)-[-(a-1)]=-a-2+a-1=-3;
当-2<a≤1时,原式=(a+2)+(a-1)= 2a+1;
当a>1时,原式=(a+2)-(a-1)=3.
12. 已知 ,求 的值.
解:∵
∴
13.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 ,善于思考的小明进行了以下探索:
设 (其中a、b、m、n均为整数),则有 这样小明就找到了一种把类似 的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若 ,
用含m、n的式子分别表示a,b,得
a=_______;b=______;
(2)利用所探索的结论,用完全平方式表示出:
(3)请化简:
m2+3n2
2mn
解:
小结与复习
第十六章 二次根式
1.通过复习理清本章的知识结构和重要知识点.
2.总结本章的重要思想方法和技能技巧.
复习目标:
一、本章知识结构图
二次根式
二次根式的化简与运算
二次根式的乘除
二次根式的加减
二、知识梳理
1.二次根式的概念
一般地,形如____(a≥0)的式子叫做二次根式.
对于二次根式的理解:
①带有二次根号;②被开方数是非负数,即a≥0.
[易错点] 二次根式中,被开方数一定是非负数,否则就没有意义.
2.二次根式的性质:
3.最简二次根式
满足下列两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含_______;
(2)被开方数中不含能___________的因数或因式.
开得尽方
分母
5.二次根式的加减:类似合并同类项
可以先将二次根式化成_____________,再将______________
的二次根式进行合并.
被开方数相同
最简二次根式
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
注意平方差公式与完全平方公式的运用!
6.二次根式的混合运算
有理数的混合运算与类似:先算乘(开)方,再算乘除,最后算加减,有括号先算括号里面的.
整式乘法运算中的乘法公式:
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
二次根式的运算律:
(1)实数运算中的运算律(交换律、结合律、分配律)和整式
乘法中的乘法公式在二次根式的运算中仍然适用.
(2)在进行计算时,能用乘法公式的要尽量使用乘法公式,
同时注意合理地运用运算律.
针对练习
1.下列各式: 中,不是二次根式的有 ( )
A.3个 B.4个 C.5个 D.6个
A
2.下列运算正确的是 ( )
C
4.若1
3.若实数a,b满足 则 .
1
5. 若等腰三角形底边长为 ,底边的高为
,则三角形的面积为 .
6.求下列二次根式中字母的取值范围:
解得 - 5≤x<3.
解:(1) 由题意得
∴x=4.
(2) 由题意得
7.将下列各数写成一个非负数的平方的形式:
8. 计算:
解:(1)原式
(2)原式
9. 交警为了估计肇事汽车在出事前的速度,总结出经验公式
,其中v是车速(单位:千米/时),d 是汽车刹车后车轮滑动的距离(单位:米),f 是摩擦系数.在某次交通事故调查中,测得d=20米,f=1.2,请你帮交警计算一下肇事汽车在出事前的速度.
解:根据题意得 (千米/时).
答:肇事汽车在出事前的速度是 千米/时.
解:原式
当 时,
原式
10. 先化简,再求值: ,其中
11. 已知a是实数,求 的值.
解: 分三种情况讨论:
当a≤-2时,原式=(-a-2)-[-(a-1)]=-a-2+a-1=-3;
当-2<a≤1时,原式=(a+2)+(a-1)= 2a+1;
当a>1时,原式=(a+2)-(a-1)=3.
12. 已知 ,求 的值.
解:∵
∴
13.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 ,善于思考的小明进行了以下探索:
设 (其中a、b、m、n均为整数),则有 这样小明就找到了一种把类似 的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若 ,
用含m、n的式子分别表示a,b,得
a=_______;b=______;
(2)利用所探索的结论,用完全平方式表示出:
(3)请化简:
m2+3n2
2mn
解:
