人教版数学八年级下册 20.2 数据的波动程度 第1课时 方差的意义 课件 (共15张PPT)
文档属性
| 名称 | 人教版数学八年级下册 20.2 数据的波动程度 第1课时 方差的意义 课件 (共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 325.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
数学 八年级下册 人教版
第二十章 数据的分析
20.2 数据的波动程度
第1课时 方差的意义
2.一组数据1,2,1,4的方差为____.
B
1.5
3.(2021·包头)某人5次射击命中的环数分别为5,10,7,x,10.若这组数据的中位数为8,则这组数据的方差为____.
3.6
知识点2:方差的应用
4.(2021·南充)据统计,某班7个学习小组上周参加“青年大学习”的人数分别为:5,5,6,6,6,7,7.下列说法错误的是( )
A.该组数据的中位数是6
B.该组数据的众数是6
C.该组数据的平均数是6
D.该组数据的方差是6
D
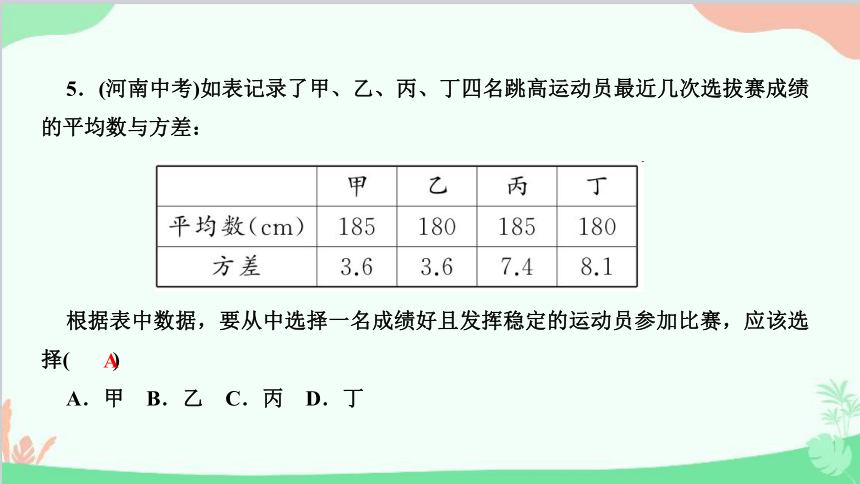
5.(河南中考)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
A
6.(2021·铜仁)若甲、乙两人参加射击训练的成绩(单位:环)如下:甲:6,7,8,9,10;乙:7,8,8,8,9.则甲、乙两人射击成绩比较稳定的是____(填“甲”或“乙”).
乙
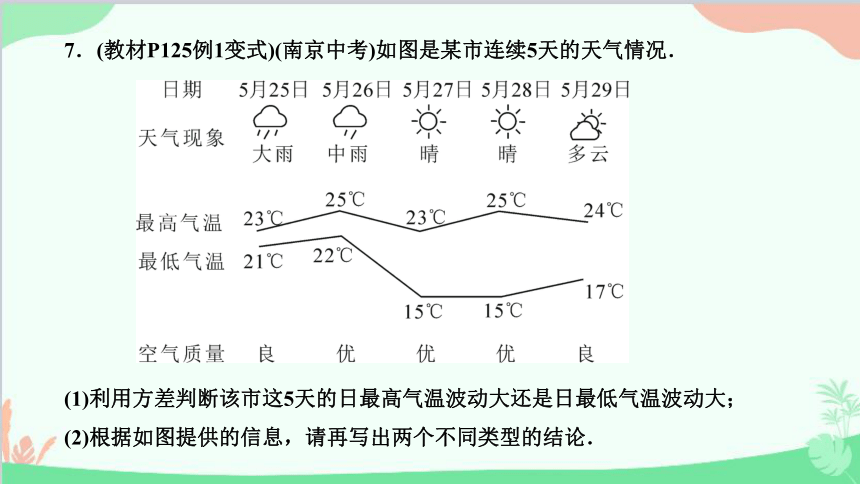
7.(教材P125例1变式)(南京中考)如图是某市连续5天的天气情况.
(1)利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大;
(2)根据如图提供的信息,请再写出两个不同类型的结论.
(2)①25日,26日,27日的天气依次为大雨、中雨、晴,空气质量依次为良、优、优,说明下雨后空气质量改善了;②该市空气质量比较好
8.(2021·枣庄)为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
则关于这组数据的结论正确的是( )
A.平均数是144 B.众数是141
C.中位数是144.5 D.方差是5.4
B
9.若样本x1+1,x2+1,x3+1,…,xn+1的平均数是10,方差为2,则样本x1+2,x2+2,x3+2,…,xn+2的平均数和方差分别是( )
A.10,2 B.11,3 C.11,2 D.12,4
10.已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是___.
C
7
11.某中学九年级甲、乙两班分别选5名同学参加“奋发向上,崇德向善”演讲比赛,其预赛成绩如图所示:
(1)根据如图信息填写下表:
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪班的成绩较好.
解:(1)甲班的众数为8.5,方差为0.7,乙的中位数为8 (2)从平均数看,两班平均数相同,则甲、乙两班的成绩一样好;从中位数看,甲班的中位数大,所以甲班的成绩较好;从众数看,乙班的众数大,所以乙班的成绩较好;从方差看,甲班的方差小,所以甲班的成绩更稳定
12.(2021·恩施州)九(1)班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同的条件下,分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表,请根据统计图表中的信息解答下列问题:
(1)求a,b的值;
(2)若九(1)班选一位成绩稳定的选手参赛,你认为应选谁,请说明理由;
(3)根据以上的数据分析,请你运用所学统计知识,任选两个角度评价甲、乙两名男生一分钟跳绳成绩谁优.
数学 八年级下册 人教版
第二十章 数据的分析
20.2 数据的波动程度
第1课时 方差的意义
2.一组数据1,2,1,4的方差为____.
B
1.5
3.(2021·包头)某人5次射击命中的环数分别为5,10,7,x,10.若这组数据的中位数为8,则这组数据的方差为____.
3.6
知识点2:方差的应用
4.(2021·南充)据统计,某班7个学习小组上周参加“青年大学习”的人数分别为:5,5,6,6,6,7,7.下列说法错误的是( )
A.该组数据的中位数是6
B.该组数据的众数是6
C.该组数据的平均数是6
D.该组数据的方差是6
D
5.(河南中考)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
A
6.(2021·铜仁)若甲、乙两人参加射击训练的成绩(单位:环)如下:甲:6,7,8,9,10;乙:7,8,8,8,9.则甲、乙两人射击成绩比较稳定的是____(填“甲”或“乙”).
乙
7.(教材P125例1变式)(南京中考)如图是某市连续5天的天气情况.
(1)利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大;
(2)根据如图提供的信息,请再写出两个不同类型的结论.
(2)①25日,26日,27日的天气依次为大雨、中雨、晴,空气质量依次为良、优、优,说明下雨后空气质量改善了;②该市空气质量比较好
8.(2021·枣庄)为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
则关于这组数据的结论正确的是( )
A.平均数是144 B.众数是141
C.中位数是144.5 D.方差是5.4
B
9.若样本x1+1,x2+1,x3+1,…,xn+1的平均数是10,方差为2,则样本x1+2,x2+2,x3+2,…,xn+2的平均数和方差分别是( )
A.10,2 B.11,3 C.11,2 D.12,4
10.已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是___.
C
7
11.某中学九年级甲、乙两班分别选5名同学参加“奋发向上,崇德向善”演讲比赛,其预赛成绩如图所示:
(1)根据如图信息填写下表:
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪班的成绩较好.
解:(1)甲班的众数为8.5,方差为0.7,乙的中位数为8 (2)从平均数看,两班平均数相同,则甲、乙两班的成绩一样好;从中位数看,甲班的中位数大,所以甲班的成绩较好;从众数看,乙班的众数大,所以乙班的成绩较好;从方差看,甲班的方差小,所以甲班的成绩更稳定
12.(2021·恩施州)九(1)班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同的条件下,分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表,请根据统计图表中的信息解答下列问题:
(1)求a,b的值;
(2)若九(1)班选一位成绩稳定的选手参赛,你认为应选谁,请说明理由;
(3)根据以上的数据分析,请你运用所学统计知识,任选两个角度评价甲、乙两名男生一分钟跳绳成绩谁优.
