华东师大版数学八年级下册 专题课堂 特殊四边形与动点问题 课件 (共13张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册 专题课堂 特殊四边形与动点问题 课件 (共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 10:07:08 | ||
图片预览




文档简介
(共13张PPT)
数学 八年级下册 华师版
第19章 矩形、菱形与正方形
专题课堂(十) 特殊四边形与动点问题
一、平行四边形与动点
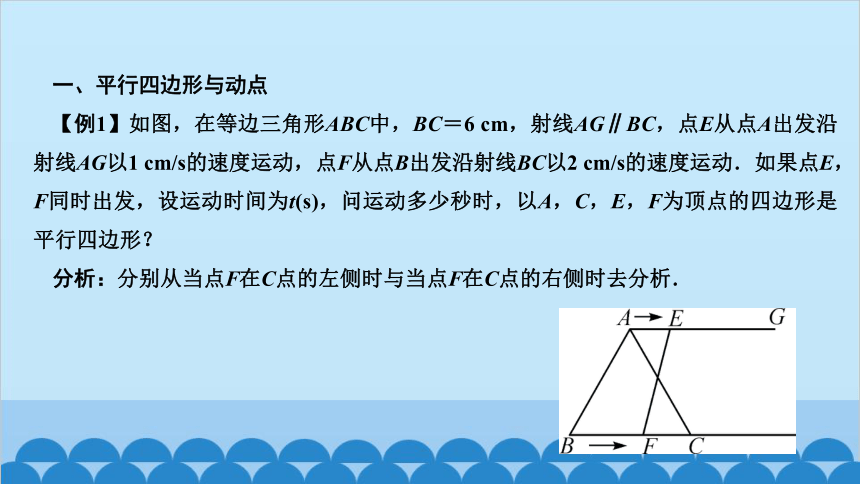
【例1】如图,在等边三角形ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,设运动时间为t(s),问运动多少秒时,以A,C,E,F为顶点的四边形是平行四边形?
分析:分别从当点F在C点的左侧时与当点F在C点的右侧时去分析.
①当点F在点C左侧时,根据题意得:AE=t cm,BF=2t cm,则CF=BC-BF=(6-2t) cm,∵AG∥BC,∴当AE=CF时,四边形AECF是平行四边形,即t=6-2t,解得t=2;②当点F在C点的右侧时,根据题意得AE=t cm,BF=2t cm,则CF=BF-BC=(2t-6) cm,∵AG∥BC,∴当AE=CF时,四边形AEFC是平行四边形,即t=2t-6,解得t=6.综上可得:当t=2 s或6 s时,以A,C,E,F为顶点的四边形是平行四边形
[对应训练]
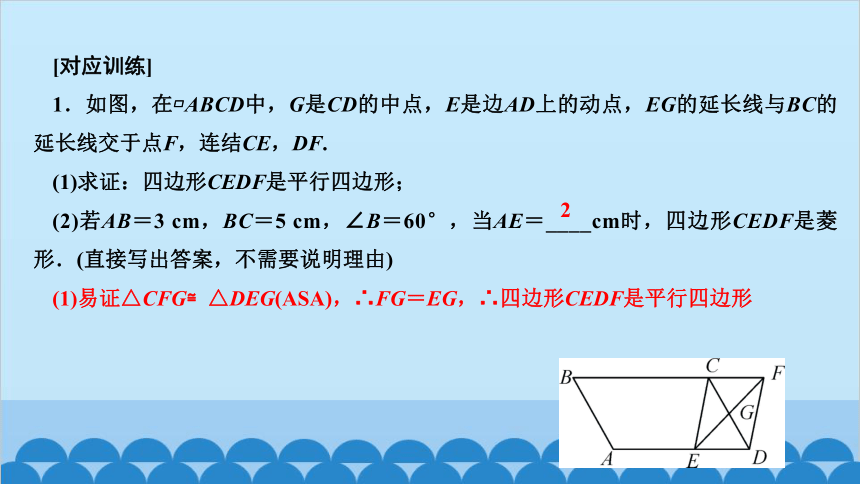
1.如图,在 ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3 cm,BC=5 cm,∠B=60°,当AE=____cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
(1)易证△CFG≌△DEG(ASA),∴FG=EG,∴四边形CEDF是平行四边形
2
二、矩形与动点
【例2】如图,在矩形ABCD中,AB=24 cm,BC=12 cm.点P沿AB边从A开始向点B以2 cm/s的速度移动;点Q沿DA边从D开始向点A以1 cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动的时间(0≤t≤12).
(1)当t=____时,△QAP为等腰直角三角形;
(2)求四边形QAPC的面积.
分析:(1)由题意得,当AP=AQ时,△QAP为等腰直角三角形,得出关于t的方程,即可解得t的值;(2)根据S=S△AQC+S△APC,即可求得.
4
[对应训练]
2.如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A,B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标.
三、菱形与动点
【例3】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连结BE.
(1)如图①所示,当点D在线段BC上时.探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图②所示,当点D在BC的延长线上运动到什么位置时,四边形BCGE是菱形?并说明理由.
(1)易证△AEB≌△ADC(SAS),∴∠ABE=∠C=60°,又∵∠BAC=∠C=60°,∴∠ABE=∠BAC,∴EB∥GC,又∵EG∥BC,∴四边形BCGE是平行四边形
(2)当CD=CB时,四边形BCGE是菱形.理由:同(1),△AEB≌△ADC,∴BE=CD,∵CD=BC,∴BE=BC,同(1)可证四边形BCGE是平行四边形,∴四边形BCGE是菱形
[对应训练]
4.如图,在正方形ABCD中,E,F分别是BC,DC边上的动点,且AE⊥EF于点E.延长EF交正方形ABCD的外角平分线CP于点P,试判断AE与EP的大小关系,并说明理由.
AE=EP.理由:在AB上截取BN=BE,∵四边形ABCD为正方形,∴AB=BC,∠B=90°,∴AN=EC,∠1=∠2=45°,∴∠4=135°,∵CP为正方形ABCD的外角平分线,∴∠PCE=135°,∴∠PCE=∠4,∵∠AEP=90°,∴∠BEA+∠3=90°,∵∠BAE+∠BEA=90°,∴∠3=∠BAE,∴△ANE≌△ECP(ASA).∴AE=EP
数学 八年级下册 华师版
第19章 矩形、菱形与正方形
专题课堂(十) 特殊四边形与动点问题
一、平行四边形与动点
【例1】如图,在等边三角形ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,设运动时间为t(s),问运动多少秒时,以A,C,E,F为顶点的四边形是平行四边形?
分析:分别从当点F在C点的左侧时与当点F在C点的右侧时去分析.
①当点F在点C左侧时,根据题意得:AE=t cm,BF=2t cm,则CF=BC-BF=(6-2t) cm,∵AG∥BC,∴当AE=CF时,四边形AECF是平行四边形,即t=6-2t,解得t=2;②当点F在C点的右侧时,根据题意得AE=t cm,BF=2t cm,则CF=BF-BC=(2t-6) cm,∵AG∥BC,∴当AE=CF时,四边形AEFC是平行四边形,即t=2t-6,解得t=6.综上可得:当t=2 s或6 s时,以A,C,E,F为顶点的四边形是平行四边形
[对应训练]
1.如图,在 ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3 cm,BC=5 cm,∠B=60°,当AE=____cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
(1)易证△CFG≌△DEG(ASA),∴FG=EG,∴四边形CEDF是平行四边形
2
二、矩形与动点
【例2】如图,在矩形ABCD中,AB=24 cm,BC=12 cm.点P沿AB边从A开始向点B以2 cm/s的速度移动;点Q沿DA边从D开始向点A以1 cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动的时间(0≤t≤12).
(1)当t=____时,△QAP为等腰直角三角形;
(2)求四边形QAPC的面积.
分析:(1)由题意得,当AP=AQ时,△QAP为等腰直角三角形,得出关于t的方程,即可解得t的值;(2)根据S=S△AQC+S△APC,即可求得.
4
[对应训练]
2.如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A,B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标.
三、菱形与动点
【例3】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连结BE.
(1)如图①所示,当点D在线段BC上时.探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图②所示,当点D在BC的延长线上运动到什么位置时,四边形BCGE是菱形?并说明理由.
(1)易证△AEB≌△ADC(SAS),∴∠ABE=∠C=60°,又∵∠BAC=∠C=60°,∴∠ABE=∠BAC,∴EB∥GC,又∵EG∥BC,∴四边形BCGE是平行四边形
(2)当CD=CB时,四边形BCGE是菱形.理由:同(1),△AEB≌△ADC,∴BE=CD,∵CD=BC,∴BE=BC,同(1)可证四边形BCGE是平行四边形,∴四边形BCGE是菱形
[对应训练]
4.如图,在正方形ABCD中,E,F分别是BC,DC边上的动点,且AE⊥EF于点E.延长EF交正方形ABCD的外角平分线CP于点P,试判断AE与EP的大小关系,并说明理由.
AE=EP.理由:在AB上截取BN=BE,∵四边形ABCD为正方形,∴AB=BC,∠B=90°,∴AN=EC,∠1=∠2=45°,∴∠4=135°,∵CP为正方形ABCD的外角平分线,∴∠PCE=135°,∴∠PCE=∠4,∵∠AEP=90°,∴∠BEA+∠3=90°,∵∠BAE+∠BEA=90°,∴∠3=∠BAE,∴△ANE≌△ECP(ASA).∴AE=EP
