物体的三视图2说课
图片预览




文档简介
课件15张PPT。三视图 这节课在学习了三视图的画法,柱、椎、台、球的表面积和体积的基础之上来进一步学习三视图,为了进一步培养高一学生空间想象能力,识别三视图所表示的几何体、学会画三视图的直观图、理解三视图的边长与几何体实际边长关系并进行简单的计算,我在查阅了课程标准和近几年使用人教B版教材的几个省市的高考题后,设计了本课。 设计初衷设计思路一、复习画三视图。练习1、(教材习题1-1A5)
画出底面边长为2cm,高为5cm的正三棱锥的三视图。 通过这道习题,复习了画几何体三视图“长对正、高平齐、宽相等”的画法和作图过程。设计意图:设计思路一、复习画三视图。练习2、几何体的直观图如图所示,画出该几何体的三视图,并找出三视图与直观图的对应边。
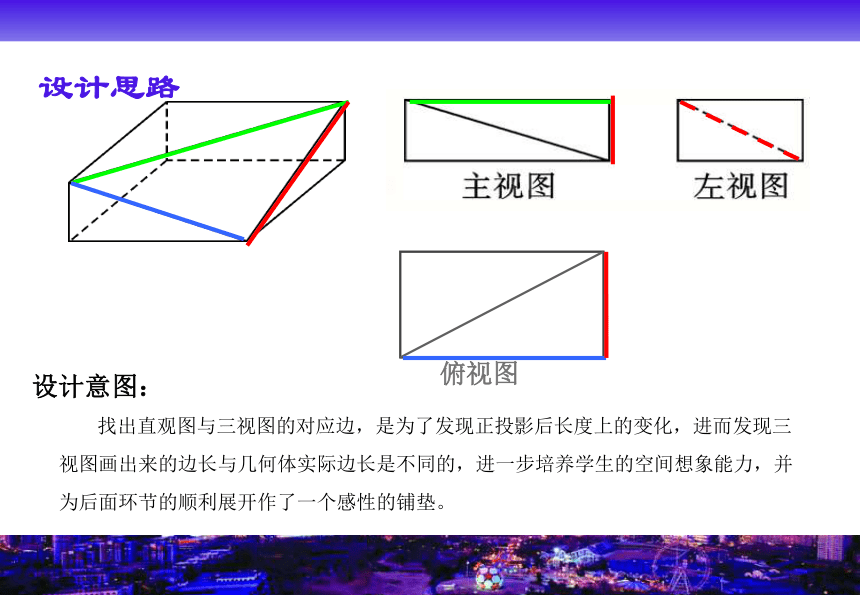
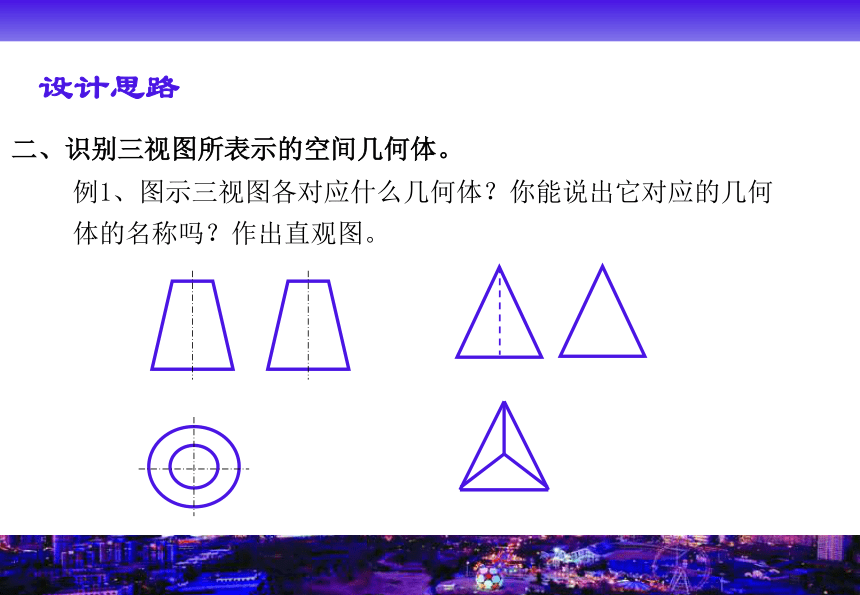
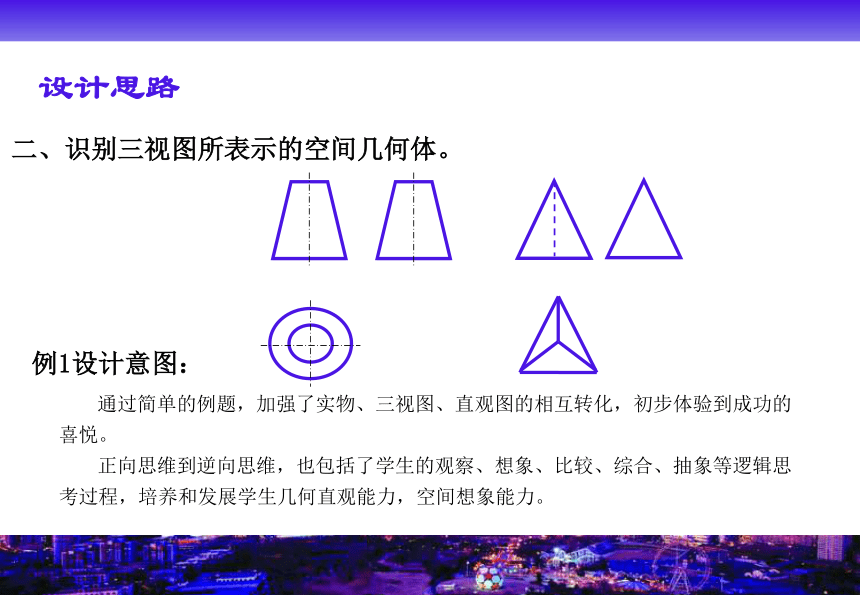
设计意图: 找出直观图与三视图的对应边,是为了发现正投影后长度上的变化,进而发现三视图画出来的边长与几何体实际边长是不同的,进一步培养学生的空间想象能力,并为后面环节的顺利展开作了一个感性的铺垫。 设计思路设计思路二、识别三视图所表示的空间几何体。例1、图示三视图各对应什么几何体?你能说出它对应的几何体的名称吗?作出直观图。例1设计意图: 通过简单的例题,加强了实物、三视图、直观图的相互转化,初步体验到成功的喜悦。
正向思维到逆向思维,也包括了学生的观察、想象、比较、综合、抽象等逻辑思考过程,培养和发展学生几何直观能力,空间想象能力。 设计思路二、识别三视图所表示的空间几何体。设计思路二、识别三视图所表示的空间几何体。设计思路二、识别三视图所表示的空间几何体。 练习3体现了三视图是不可分割的整体,交给学生独立思考完成,加强学生识别三视图的能力,加深对三视图的认识,即看几何体要从不同角度去认识、分析、解决;推广到对社会乃至人生的认识,也要多角度分析,从而以积极向上的心态对待社会和人生。练习3设计意图:设计思路三、根据三视图进行简单的计算。例2、(教材习题1-1B 2)一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积。设计思路三、根据三视图进行简单的计算。例2设计意图: 有了前两部分的铺垫,例2的展开水到渠成,这也符合新课标在立体几何内容编排上的特点:即从整体到局部,从对几何体的整体认识到度量认识,关注了学生的思维过程,也提高了学生的应用意识。
有关三视图的计算问题通常要分两步走:1. 实物、三视图、直观图的相互转化;2.准确的计算出实际长度。
由三视图想象几何体时也要根据“长对正、高平齐、宽相等”的原则,想象视图中每部分对应的几何体的形象,这也是准确计算的前提。设计思路三、根据三视图进行简单的计算。练习4、如图是一个空间几何体的三视图,则它的体积是 . 与例题一样,都是关于三棱柱的计算问题,同时又让学生通过实例认识到:同一个几何体,放的位置不同,其三视图的形状也会发生改变,提高识图能力。 设计意图:设计思路三、根据三视图进行简单的计算。选做题:练习5(2009辽宁高考16题)设某几何体的三视图如下(尺寸的长度单位为m)。则该几何体的体积为 。这道练习题对高一的学生有一定难度,很难将实物、三视图、直观图进行相互转化,但也正因为其挑战性会激起有能力学生的学习热情,作为选做题,使不同层次的学生在原有的基础上都有所收获。设计意图:设计反思一、前两部分作为第三部分的铺垫,在思路上符合学生从整体到局部的认识过程,即对几何体的整体认识到度量认识。 二、在能力培养上也符合高初中衔接的特点,增加了识图、准确画图,各种视图间的转化,并进行计算,这个过程中包括了学生的观察、想象、比较、综合、抽象等逻辑思考过程,培养和发展学生几何直观能力,空间想象能力。 三、两道典型例题,5道富于层次的练习题,让学生多看、多画、多想象,充分体现了立体几何这个部分以学生为主体的教学思想。也让平时的教学更贴近高考。谢谢!大连市第十五中学 孙琳琳课件15张PPT。三视图 这节课在学习了三视图的画法,柱、椎、台、球的表面积和体积的基础之上来进一步学习三视图,为了进一步培养高一学生空间想象能力,识别三视图所表示的几何体、学会画三视图的直观图、理解三视图的边长与几何体实际边长关系并进行简单的计算,我在查阅了课程标准和近几年使用人教B版教材的几个省市的高考题后,设计了本课。 设计初衷设计思路一、复习画三视图。练习1、(教材习题1-1A5)
画出底面边长为2cm,高为5cm的正三棱锥的三视图。 通过这道习题,复习了画几何体三视图“长对正、高平齐、宽相等”的画法和作图过程。设计意图:设计思路一、复习画三视图。练习2、几何体的直观图如图所示,画出该几何体的三视图,并找出三视图与直观图的对应边。
设计意图: 找出直观图与三视图的对应边,是为了发现正投影后长度上的变化,进而发现三视图画出来的边长与几何体实际边长是不同的,进一步培养学生的空间想象能力,并为后面环节的顺利展开作了一个感性的铺垫。 设计思路设计思路二、识别三视图所表示的空间几何体。例1、图示三视图各对应什么几何体?你能说出它对应的几何体的名称吗?作出直观图。例1设计意图: 通过简单的例题,加强了实物、三视图、直观图的相互转化,初步体验到成功的喜悦。
正向思维到逆向思维,也包括了学生的观察、想象、比较、综合、抽象等逻辑思考过程,培养和发展学生几何直观能力,空间想象能力。 设计思路二、识别三视图所表示的空间几何体。设计思路二、识别三视图所表示的空间几何体。设计思路二、识别三视图所表示的空间几何体。 练习3体现了三视图是不可分割的整体,交给学生独立思考完成,加强学生识别三视图的能力,加深对三视图的认识,即看几何体要从不同角度去认识、分析、解决;推广到对社会乃至人生的认识,也要多角度分析,从而以积极向上的心态对待社会和人生。练习3设计意图:设计思路三、根据三视图进行简单的计算。例2、(教材习题1-1B 2)一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积。设计思路三、根据三视图进行简单的计算。例2设计意图: 有了前两部分的铺垫,例2的展开水到渠成,这也符合新课标在立体几何内容编排上的特点:即从整体到局部,从对几何体的整体认识到度量认识,关注了学生的思维过程,也提高了学生的应用意识。
有关三视图的计算问题通常要分两步走:1. 实物、三视图、直观图的相互转化;2.准确的计算出实际长度。
由三视图想象几何体时也要根据“长对正、高平齐、宽相等”的原则,想象视图中每部分对应的几何体的形象,这也是准确计算的前提。设计思路三、根据三视图进行简单的计算。练习4、如图是一个空间几何体的三视图,则它的体积是 . 与例题一样,都是关于三棱柱的计算问题,同时又让学生通过实例认识到:同一个几何体,放的位置不同,其三视图的形状也会发生改变,提高识图能力。 设计意图:设计思路三、根据三视图进行简单的计算。选做题:练习5(2009辽宁高考16题)设某几何体的三视图如下(尺寸的长度单位为m)。则该几何体的体积为 。这道练习题对高一的学生有一定难度,很难将实物、三视图、直观图进行相互转化,但也正因为其挑战性会激起有能力学生的学习热情,作为选做题,使不同层次的学生在原有的基础上都有所收获。设计意图:设计反思一、前两部分作为第三部分的铺垫,在思路上符合学生从整体到局部的认识过程,即对几何体的整体认识到度量认识。 二、在能力培养上也符合高初中衔接的特点,增加了识图、准确画图,各种视图间的转化,并进行计算,这个过程中包括了学生的观察、想象、比较、综合、抽象等逻辑思考过程,培养和发展学生几何直观能力,空间想象能力。 三、两道典型例题,5道富于层次的练习题,让学生多看、多画、多想象,充分体现了立体几何这个部分以学生为主体的教学思想。也让平时的教学更贴近高考。谢谢!大连市第十五中学 孙琳琳
画出底面边长为2cm,高为5cm的正三棱锥的三视图。 通过这道习题,复习了画几何体三视图“长对正、高平齐、宽相等”的画法和作图过程。设计意图:设计思路一、复习画三视图。练习2、几何体的直观图如图所示,画出该几何体的三视图,并找出三视图与直观图的对应边。
设计意图: 找出直观图与三视图的对应边,是为了发现正投影后长度上的变化,进而发现三视图画出来的边长与几何体实际边长是不同的,进一步培养学生的空间想象能力,并为后面环节的顺利展开作了一个感性的铺垫。 设计思路设计思路二、识别三视图所表示的空间几何体。例1、图示三视图各对应什么几何体?你能说出它对应的几何体的名称吗?作出直观图。例1设计意图: 通过简单的例题,加强了实物、三视图、直观图的相互转化,初步体验到成功的喜悦。
正向思维到逆向思维,也包括了学生的观察、想象、比较、综合、抽象等逻辑思考过程,培养和发展学生几何直观能力,空间想象能力。 设计思路二、识别三视图所表示的空间几何体。设计思路二、识别三视图所表示的空间几何体。设计思路二、识别三视图所表示的空间几何体。 练习3体现了三视图是不可分割的整体,交给学生独立思考完成,加强学生识别三视图的能力,加深对三视图的认识,即看几何体要从不同角度去认识、分析、解决;推广到对社会乃至人生的认识,也要多角度分析,从而以积极向上的心态对待社会和人生。练习3设计意图:设计思路三、根据三视图进行简单的计算。例2、(教材习题1-1B 2)一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积。设计思路三、根据三视图进行简单的计算。例2设计意图: 有了前两部分的铺垫,例2的展开水到渠成,这也符合新课标在立体几何内容编排上的特点:即从整体到局部,从对几何体的整体认识到度量认识,关注了学生的思维过程,也提高了学生的应用意识。
有关三视图的计算问题通常要分两步走:1. 实物、三视图、直观图的相互转化;2.准确的计算出实际长度。
由三视图想象几何体时也要根据“长对正、高平齐、宽相等”的原则,想象视图中每部分对应的几何体的形象,这也是准确计算的前提。设计思路三、根据三视图进行简单的计算。练习4、如图是一个空间几何体的三视图,则它的体积是 . 与例题一样,都是关于三棱柱的计算问题,同时又让学生通过实例认识到:同一个几何体,放的位置不同,其三视图的形状也会发生改变,提高识图能力。 设计意图:设计思路三、根据三视图进行简单的计算。选做题:练习5(2009辽宁高考16题)设某几何体的三视图如下(尺寸的长度单位为m)。则该几何体的体积为 。这道练习题对高一的学生有一定难度,很难将实物、三视图、直观图进行相互转化,但也正因为其挑战性会激起有能力学生的学习热情,作为选做题,使不同层次的学生在原有的基础上都有所收获。设计意图:设计反思一、前两部分作为第三部分的铺垫,在思路上符合学生从整体到局部的认识过程,即对几何体的整体认识到度量认识。 二、在能力培养上也符合高初中衔接的特点,增加了识图、准确画图,各种视图间的转化,并进行计算,这个过程中包括了学生的观察、想象、比较、综合、抽象等逻辑思考过程,培养和发展学生几何直观能力,空间想象能力。 三、两道典型例题,5道富于层次的练习题,让学生多看、多画、多想象,充分体现了立体几何这个部分以学生为主体的教学思想。也让平时的教学更贴近高考。谢谢!大连市第十五中学 孙琳琳课件15张PPT。三视图 这节课在学习了三视图的画法,柱、椎、台、球的表面积和体积的基础之上来进一步学习三视图,为了进一步培养高一学生空间想象能力,识别三视图所表示的几何体、学会画三视图的直观图、理解三视图的边长与几何体实际边长关系并进行简单的计算,我在查阅了课程标准和近几年使用人教B版教材的几个省市的高考题后,设计了本课。 设计初衷设计思路一、复习画三视图。练习1、(教材习题1-1A5)
画出底面边长为2cm,高为5cm的正三棱锥的三视图。 通过这道习题,复习了画几何体三视图“长对正、高平齐、宽相等”的画法和作图过程。设计意图:设计思路一、复习画三视图。练习2、几何体的直观图如图所示,画出该几何体的三视图,并找出三视图与直观图的对应边。
设计意图: 找出直观图与三视图的对应边,是为了发现正投影后长度上的变化,进而发现三视图画出来的边长与几何体实际边长是不同的,进一步培养学生的空间想象能力,并为后面环节的顺利展开作了一个感性的铺垫。 设计思路设计思路二、识别三视图所表示的空间几何体。例1、图示三视图各对应什么几何体?你能说出它对应的几何体的名称吗?作出直观图。例1设计意图: 通过简单的例题,加强了实物、三视图、直观图的相互转化,初步体验到成功的喜悦。
正向思维到逆向思维,也包括了学生的观察、想象、比较、综合、抽象等逻辑思考过程,培养和发展学生几何直观能力,空间想象能力。 设计思路二、识别三视图所表示的空间几何体。设计思路二、识别三视图所表示的空间几何体。设计思路二、识别三视图所表示的空间几何体。 练习3体现了三视图是不可分割的整体,交给学生独立思考完成,加强学生识别三视图的能力,加深对三视图的认识,即看几何体要从不同角度去认识、分析、解决;推广到对社会乃至人生的认识,也要多角度分析,从而以积极向上的心态对待社会和人生。练习3设计意图:设计思路三、根据三视图进行简单的计算。例2、(教材习题1-1B 2)一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积。设计思路三、根据三视图进行简单的计算。例2设计意图: 有了前两部分的铺垫,例2的展开水到渠成,这也符合新课标在立体几何内容编排上的特点:即从整体到局部,从对几何体的整体认识到度量认识,关注了学生的思维过程,也提高了学生的应用意识。
有关三视图的计算问题通常要分两步走:1. 实物、三视图、直观图的相互转化;2.准确的计算出实际长度。
由三视图想象几何体时也要根据“长对正、高平齐、宽相等”的原则,想象视图中每部分对应的几何体的形象,这也是准确计算的前提。设计思路三、根据三视图进行简单的计算。练习4、如图是一个空间几何体的三视图,则它的体积是 . 与例题一样,都是关于三棱柱的计算问题,同时又让学生通过实例认识到:同一个几何体,放的位置不同,其三视图的形状也会发生改变,提高识图能力。 设计意图:设计思路三、根据三视图进行简单的计算。选做题:练习5(2009辽宁高考16题)设某几何体的三视图如下(尺寸的长度单位为m)。则该几何体的体积为 。这道练习题对高一的学生有一定难度,很难将实物、三视图、直观图进行相互转化,但也正因为其挑战性会激起有能力学生的学习热情,作为选做题,使不同层次的学生在原有的基础上都有所收获。设计意图:设计反思一、前两部分作为第三部分的铺垫,在思路上符合学生从整体到局部的认识过程,即对几何体的整体认识到度量认识。 二、在能力培养上也符合高初中衔接的特点,增加了识图、准确画图,各种视图间的转化,并进行计算,这个过程中包括了学生的观察、想象、比较、综合、抽象等逻辑思考过程,培养和发展学生几何直观能力,空间想象能力。 三、两道典型例题,5道富于层次的练习题,让学生多看、多画、多想象,充分体现了立体几何这个部分以学生为主体的教学思想。也让平时的教学更贴近高考。谢谢!大连市第十五中学 孙琳琳
