24.2.2_直线和圆的位置关系说课_课件
文档属性
| 名称 | 24.2.2_直线和圆的位置关系说课_课件 |  | |
| 格式 | zip | ||
| 文件大小 | 406.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-18 21:11:55 | ||
图片预览





文档简介
课件29张PPT。直线与圆的位置关系24.2.2一.说 教 材地位作用 学情分析 重点难点 教学目标 本节课选自人教版数学九年级上册第24章第1节《圆》第1课时。圆是常见的几何图形之一,不仅在日常生活中的许多物体是圆形的,而且在工农业生产,交通运输,土木建筑等方面都可以看到圆。第一节是在小学学过的一些圆的知识的基础上,系统的研究圆中的一些相关概念。圆的概念又是进一步研究圆和其他图形的位置,数量关系的依据,是全章的基础。 九年级学生已经具备了一定的归纳的能力,思维活跃,求知欲、创造欲强,这是探索活动中必备的心理状态,但是同学们的实际水平有所不同,全面深入探究问题能力有所差异,他们对问题的理性推理有待于提高。
知识与技能: 1.探索并了解直线和圆的位置关系.2.根据圆心到直线的距离与圆的半径之间的数量关系揭示直线和圆的位置关系.3.能够利用公共点个数和数量关系来判断直线和圆的位置关系
过程与方法:1. 经历操作、观察、发现、总结的过程,培养学生观察、比较、概括的逻辑思维能力.2. 经历探索圆心到直线的距离与圆的半径的数量关系的过程,培养学生运用数学语言表述问题的能力.
情感目标:经过观察、实验、发现、确认等数学活动,在探索直线和圆位置关系的过程中,体会运动变化的观点,量变到质变的辩证唯物主义观点,感受数学中的美感. . .重点:探索并了解直线和圆的位置关系
难点:掌握识别直线和圆的位置关系的方法.
关键:通过问题情景的设计,引导学生
发现、分析和解决问题.地位作用 学情分析 重点难点 二.说 教 法 四.说教学过程自
主
探
究
探
究
新
知
创
设
情
景
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
问
题
引
申
形
成
技
能
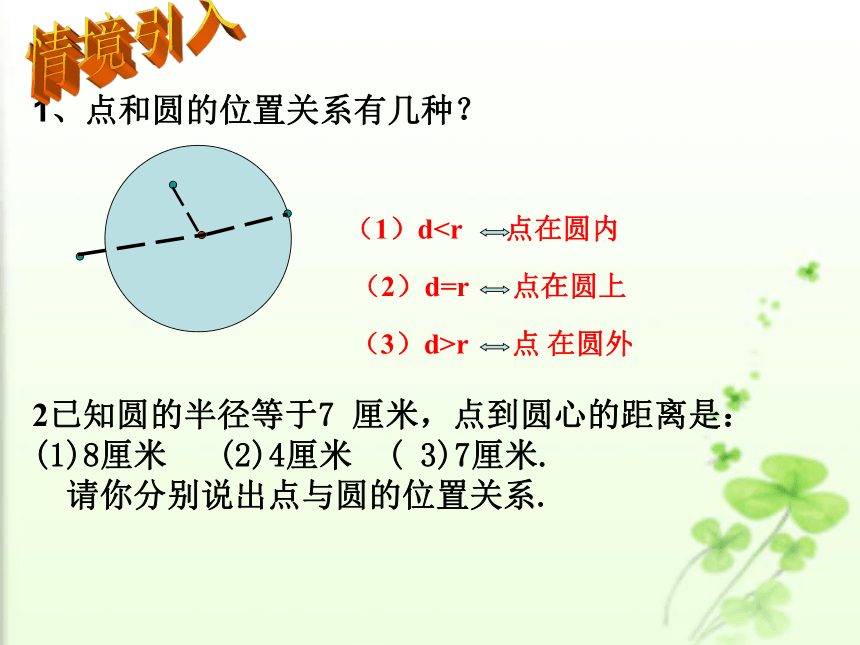
1、点和圆的位置关系有几种?2已知圆的半径等于7 厘米,点到圆心的距离是:(1)8厘米 (2)4厘米 ( 3)7厘米.
请你分别说出点与圆的位置关系.情境引入“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,请你根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?
驶向胜利的彼岸作一个圆,把直尺边缘看成一条直线.
固定圆, 平移直尺,直线和圆有哪几种位置关系?有三种位置关系:相交相切相离自学质疑一、直线 与圆的位置关系1、如图1,直线与圆_______公共点,那么这条直线与圆_________。2、如图2,直线与圆只有______公共点时,那么直线与圆________。此时,这条直线叫做圆的_______,这个公共点叫做_______。3、如图3,直线与圆有_______公共点时,那么直线与圆________。此时,这条直线叫做________,这两个公共点叫做_______。图 1图 2图 3相切没有 一个切线切点两个相交割线相离 交点精讲点拨 直线和圆的位置关系是用直线和圆的公共点的个数来定义的,即直线与圆没有公共点、只有一个公共点、有两个公共点时分别叫做直线和圆相离、相切、相交。相离相交相切切点切线割线即直线与圆是否有第三个交点?是是非非×.C1.若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )是是非非 2.、直线与圆最多有两个公共
点 。…………………( ) √是是非非3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )×是是非非√4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )根据直线与圆的公共点的个数来判断直线与圆的位置关系 新的问题:是否还有其它的方法来判断直线与圆的位置关系?ddd.O.O.Orrr相离相切相交1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d<
<
看一看想一想当直线与圆相离、相切、
相交时,d与r有何关系?lll.A.B.
C.D.E.F. NH.Q.d表示圆心O到直线l
的距离,r表示⊙O
的半径1、已知⊙O的半径为5cm,O到
直线a的距离为3cm,则⊙O与直
线a的位置关系是_____。直线a
与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。动动脑筋相交 相切两个
3、已知⊙O的半径为6cm,O到
直线a的距离为7cm,则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。零相离归纳直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r没有例题1:.AO已知⊙A的直径为6,点A的坐标为
(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切习练(二):1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=42、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交CD解: 过C点作CD⊥AB,垂足为D
∴ AB = 5
∴3×4 = 5×CD讨论:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当r满足________________时,⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满足____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cmAC=3cm,BC=4cm,
以C为圆心,r为半径作圆。想一想? 当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm2、识别直线与圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线L与⊙o没有公共点 直线L与⊙o相离。
直线L与⊙o只有一个公共点 直线L与⊙o相切。
直线L与⊙o有两个公共点 直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
d>r 直线L与⊙o相离;
d=r 直线L与⊙o相切;
d1、直线与圆的位置关系3种:相离、相切和相交。课堂小结
知识与技能: 1.探索并了解直线和圆的位置关系.2.根据圆心到直线的距离与圆的半径之间的数量关系揭示直线和圆的位置关系.3.能够利用公共点个数和数量关系来判断直线和圆的位置关系
过程与方法:1. 经历操作、观察、发现、总结的过程,培养学生观察、比较、概括的逻辑思维能力.2. 经历探索圆心到直线的距离与圆的半径的数量关系的过程,培养学生运用数学语言表述问题的能力.
情感目标:经过观察、实验、发现、确认等数学活动,在探索直线和圆位置关系的过程中,体会运动变化的观点,量变到质变的辩证唯物主义观点,感受数学中的美感. . .重点:探索并了解直线和圆的位置关系
难点:掌握识别直线和圆的位置关系的方法.
关键:通过问题情景的设计,引导学生
发现、分析和解决问题.地位作用 学情分析 重点难点 二.说 教 法 四.说教学过程自
主
探
究
探
究
新
知
创
设
情
景
导
入
新
课
合
作
交
流
巩
固
提
高
课
堂
小
结
布
置
作
业
问
题
引
申
形
成
技
能
1、点和圆的位置关系有几种?2已知圆的半径等于7 厘米,点到圆心的距离是:(1)8厘米 (2)4厘米 ( 3)7厘米.
请你分别说出点与圆的位置关系.情境引入“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,请你根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?
驶向胜利的彼岸作一个圆,把直尺边缘看成一条直线.
固定圆, 平移直尺,直线和圆有哪几种位置关系?有三种位置关系:相交相切相离自学质疑一、直线 与圆的位置关系1、如图1,直线与圆_______公共点,那么这条直线与圆_________。2、如图2,直线与圆只有______公共点时,那么直线与圆________。此时,这条直线叫做圆的_______,这个公共点叫做_______。3、如图3,直线与圆有_______公共点时,那么直线与圆________。此时,这条直线叫做________,这两个公共点叫做_______。图 1图 2图 3相切没有 一个切线切点两个相交割线相离 交点精讲点拨 直线和圆的位置关系是用直线和圆的公共点的个数来定义的,即直线与圆没有公共点、只有一个公共点、有两个公共点时分别叫做直线和圆相离、相切、相交。相离相交相切切点切线割线即直线与圆是否有第三个交点?是是非非×.C1.若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )是是非非 2.、直线与圆最多有两个公共
点 。…………………( ) √是是非非3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )×是是非非√4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )根据直线与圆的公共点的个数来判断直线与圆的位置关系 新的问题:是否还有其它的方法来判断直线与圆的位置关系?ddd.O.O.Orrr相离相切相交1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d
<
看一看想一想当直线与圆相离、相切、
相交时,d与r有何关系?lll.A.B.
C.D.E.F. NH.Q.d表示圆心O到直线l
的距离,r表示⊙O
的半径1、已知⊙O的半径为5cm,O到
直线a的距离为3cm,则⊙O与直
线a的位置关系是_____。直线a
与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。动动脑筋相交 相切两个
3、已知⊙O的半径为6cm,O到
直线a的距离为7cm,则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。零相离归纳直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r没有例题1:.AO已知⊙A的直径为6,点A的坐标为
(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切习练(二):1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=42、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交CD解: 过C点作CD⊥AB,垂足为D
∴ AB = 5
∴3×4 = 5×CD讨论:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当r满足________________时,⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满足____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cm
以C为圆心,r为半径作圆。想一想? 当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm
(1)一种是根据定义进行识别:
直线L与⊙o没有公共点 直线L与⊙o相离。
直线L与⊙o只有一个公共点 直线L与⊙o相切。
直线L与⊙o有两个公共点 直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
d>r 直线L与⊙o相离;
d=r 直线L与⊙o相切;
d
同课章节目录
